M估计补充策略下的三轴磁传感器误差补偿

潘惠坤, 李胜, 钱晨, 季蔡娟, 徐振

(南京理工大学自动化学院, 210094, 南京)

地球磁场是地球系统的基本物理场之一,因为其无源、稳定且与地理位置有关的优点,利用其进行导航的地磁匹配导航技术受到了学者们的关注[1-4]。与其他辅助导航技术相比,地磁匹配导航技术具有无源自主、误差不随时间累积、全天候、隐蔽性强、连续导航、适用范围广的优点[5]。获取高精度的地磁数据是地磁匹配导航的关键之一,决定着导航的精度。

三轴磁传感器进行地磁场强度测量时,磁场数据不可避免的会包含误差和异常值。误差可以分为磁测系统误差和外界磁干扰两类。磁测系统误差包括三轴磁传感器自身的误差(三轴磁传感器在制造过程中的零偏误差、非正交误差、刻度因子误差等)以及磁测系统的安装误差[6],外界磁干扰包括传感器周围的载体磁场及磁日变磁场等干扰信息。这些误差使得磁传感器测得的数据无法直接用来进行地磁匹配,需要对测量值进行校准。因此,需要研究高精度的磁传感器误差补偿算法。

常用的磁传感器误差校准方法分为辅助矢量校正方法和独立标量校正方法两类。辅助矢量校正方法通过与已知的磁矢量场比较从而对磁传感器数据进行辅助校正参考[7-8]。然而,在实际应用中,难以获取高精度的已知磁场矢量。独立标量校正法则可以避免该缺点,通过三轴磁传感器在恒定磁场内旋转,以合成总场是固定值作为约束条件对其进行校正。独立标量校正方法因其在实际环境中易操作的优点吸引了大量学者的研究,典型代表为基于椭球假设的磁补偿方法[9-10]。文献[11]中提出了基于最小二乘法的误差标定方法并应用于磁航向误差补偿中,测试结果满足精度要求;文献[12]利用自适应最小二乘估计法解决了椭球体拟合问题,取得了良好的校正效果;文献[13]设计了一种基于自适应遗传算法的空间椭球磁强计校准方法,能够同时兼顾三轴磁传感器误差及其安装误差;文献[14]提出了基于递推最小二乘法的三轴磁传感器误差在线自校正方法。基于椭球假设的磁补偿方法是最常见的磁传感器标定和补偿方法,并广泛应用于实际测量中。

这些算法均假设三轴磁传感器测量时不包含误差较大的采样点或异常值。然而,在实际测量中,该假设不成立,并会对最终精度造成较大影响。M估计法是一种有效提高系统鲁棒性的技术[15]。通过构造权重代价函数,获得与采样点残差相对应的权重值,降低甚至消除异常点造成的影响,从而增强系统鲁棒性提高精度[16]。

基于这一思路,本文提出了M估计补充策略下的三轴磁传感器误差补偿算法。在最小二乘法的椭球拟合算法的基础上,引入M估计的思想,根据其拟合的残差数据,构造Huber权重目标函数,确定各个采样点的权重,为偏离较大的采样点设置低权重,为偏离较小的点设置高权重,对数据进行灵活处理,从而增强系统鲁棒性,降低异常点对拟合的影响,最终提高地磁测量的精度。

1 地磁传感器误差分析与建模

1.1 地磁传感器误差分析

地磁传感器误差主要由载体磁场误差和自身误差组成。

载体磁场误差是由磁传感器周围的各种磁性材料造成的。载体磁场误差是地磁场测量中所特有的一种误差,可以分为硬磁误差、软磁误差以及随机磁场误差共3类主要误差。

三轴磁传感器在实际使用过程中,存在安装差异,即自身误差。传感器误差来源主要有3类:三轴灵敏度不一致造成的灵敏度误差、传感器三轴未完全正交造成的非正交误差以及传感器的零位偏移误差。自身误差属于机械误差,比较固定,出厂后不易改变。

1.2 地磁传感器误差模型建模

综合考虑载体磁场误差和自身误差,参考文献[17]建立误差模型

Hm=CsiCn(CsHe+bh)+b0+ε

(1)

将式(1)简化可得

Hm=CHe+b+ε

(2)

式中:C=CsiCnCs;b=CsiCnbh+b0。显然,C是可逆矩阵,因此可以得到地磁场误差校正模型

He=C-1(Hm-b-ε)

(3)

在求出校准矩阵C-1和偏移量b的基础上,当获得磁传感器量测数据后,通过式(3)可以计算出当地的真实地磁强度,式中ε可以通过合理的硬件技术手段减小,因此计算过程中可以忽略。

2 椭球拟合算法

在磁场强度恒定的区域内对磁传感器进行任意旋转,测量出的磁场应该是一个定值,即磁场矢量的轨迹应该是一个正球体,可表达为

‖He‖2=Cconst

(4)

式中Cconst代表磁场强度的定值。结合式(2)(4)得

‖He‖2=HeTHe=

(Hm-b)T(C-1)TC-1(Hm-b)

(5)

进一步转化,得到

(6)

对式(6)进行化简,得到

(7)

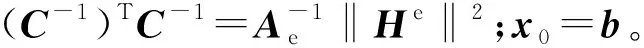
椭球方程的一般形式为

a1X2+b1Y2+c1Z2+2f1XY+2g1XZ+

2h1YZ+2p1X+2q1Y+2r1Z+d1=0

(8)

为方便后续计算,将式(8)归一化为

aX2+bY2+cZ2+2fXY+2gXZ+
2hYZ+2pX+2qY+2rZ=1

(9)

将(9)式写成向量形式,则有

Hiξ=1

(10)

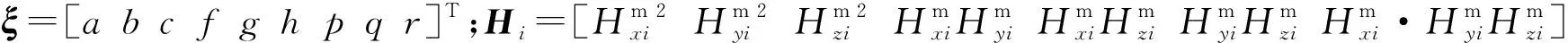
至此,磁场量测值拟合的椭球面参数已经获得。下一步求解校准矩阵C-1和偏移量b。将式(9)转化为矩阵形式

HmTEHm+(2F)THm+G=0

(11)

建立式(11)与式(7)之间的联系,对式(11)进行转换可得

HmTEHm+2FTHm+G=0

⟹HmTEHm+FTHm+HmTF+G=0

⟹(HmT+FTE-1)EHm+HmTF=-G

⟹(HmT+FTE-1)(EHm+F)=FTE-1F-G

⟹(HmT+FTE-1)E(Hm+E-1F)=FTE-1F-G

⟹(Hm+E-1F)TE(Hm+E-1F)=FTE-1F-G

(12)

结合式(6)(7)(12),得到

b=x0=-E-1F

(13)

(14)

对式(14)进一步转化可得

(15)

通过式(13)(15)得到校准矩阵C-1和偏移矢量b,结合式(3)可求出实际地磁场数据,完成误差补偿。

3 M估计补充策略下的误差补偿算法

当数据中包含离群点的时候,式(10)中ξ的估计将受到严重的影响,利用最小二乘法对磁场数据进行椭球拟合时,无法有效消除异常点带来的影响,其精度无法得到保证。为此,本文引入M估计算法解决上述问题。鲁棒M估计通过自适应地为样本分配不同的权值(为离群点分配接近于0的权值),消除离群点对模型参数估计结果的影响。因此ξ的M估计相当于椭球面参数的优化问题。

3.1 M估计算法

在数据采集过程中,会不可避免地出现一些异常值。最小二乘法即

(16)

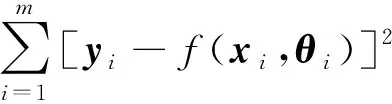
M估计是1964年由Huber提出的,是最常用的稳健估计算法[18]。基本思想是采用迭代加权最小二乘估计回归系数,根据回归残差的大小确定各点的权值,从而达到稳健的目的。M估计一般定义为

(17)

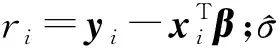
(18)

式中med为取中位数函数。

对于式(17),不同的目标函数最后的效果都差不多。本文使用Huber法,其目标函数为

(19)

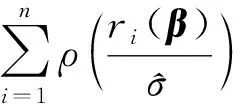
(20)

式中ψ0(u)是ρ(u)的导数,公式为

(21)

权重代价函数定义为ω(u)=ψ0(u)/u,则式(20)变为

(22)

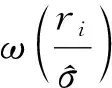
(23)

其中k为可调参数。不同的k对各采样点的权重会有一定的影响。通常k取为1.345,此时估计算法既是稳健的,又有较高的估计效率。后文4.1小节实验也证明了该数值下本文算法的有效性。

M估计的估计方程写成矩阵形式为

XTWXβ=XTWY

(24)

迭代公式为

(25)

式中:W是以Wi为对角元的权矩阵,i=1,2,…,n;X是解释变量矩阵,X=[x1,x2,…,xn]T;Y是因变量向量,Y=[y1,y2,…,yn]T。

3.2 M估计补充策略下的磁传感器误差补偿算法

在磁场内部旋转磁传感器,得到采样数据,将采样数据代入地磁传感器误差模型中,然后设计M估计补充策略下的磁传感器误差补偿算法,步骤如下。

步骤1 初始化。通过最小二乘法得到的椭球面参数的估计值ξ(0)作为回归系数初始值。

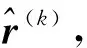
步骤3 权重获取。将标准化残差代入权函数中,得到各采样点权重,并构成权重函数矩阵W(k)。

步骤4 椭球参数更新。由式(25)进行拓展,得到椭球面参数更新公式为

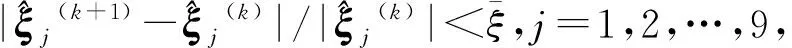
步骤6 校准矩阵和偏移矢量求取。根据式(12)～(15)得到校准矩阵C-1和偏移矢量b,完成误差补偿。

4 数值分析与实验验证

4.1 仿真验证

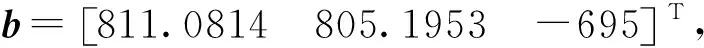
在该椭球面上选取1 200个点并叠加高斯白噪声ε作为磁传感器量测值,其中ε=[εx,εy,εz]T;εx,εy,εz～N(0,150 nT2)。随机插入100个异常值ηi,ηi=[ηix,ηiy,ηiz]T;ηix,ηiy,ηiz～U(-50 000 nT,50 000 nT)。模拟出1 300个测量数据,分布见图1。

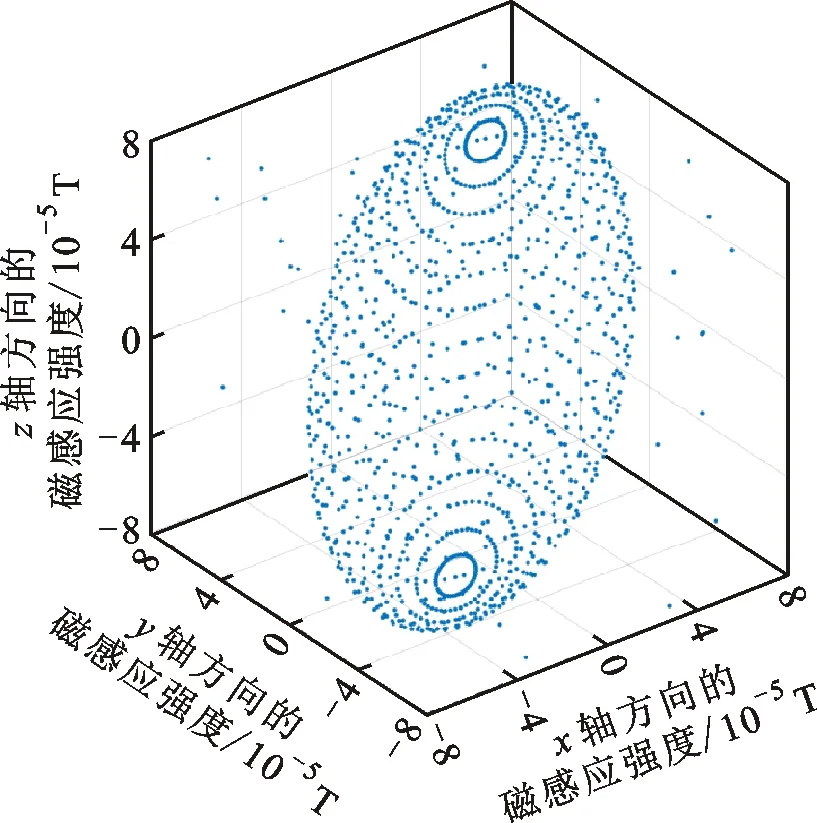
图1 模拟的测量数据Fig.1 Simulated measurement data

对模拟出的测量数据分别用最小二乘法、递推最小二乘法和M估计补充策略下的误差补偿算法进行椭球拟合。3种算法拟合出的椭球面如图2所示。可以看出,递推最小二乘法拟合的椭球面受到异常值的影响最大,这是因为在递推最小二乘法中,越晚采集到的数据所占权重越大,如果这些数据中有偏离值,则会严重影响拟合效果。

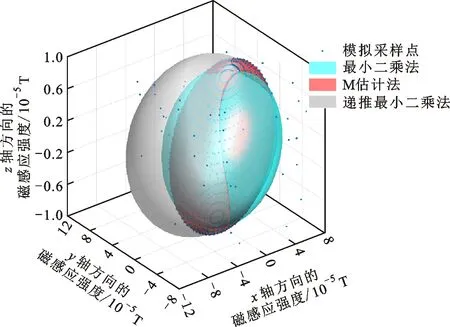
图2 椭球拟合结果对比Fig.2 Comparison of results of ellipsoid fitting algorithm

将测量、最小二乘法校正后、递推最小二乘法校正后、M估计法校正后的三轴磁场数据转化为总磁场强度,结果如图3所示。可以看出:未校正数据波动较大;3种算法校正后的数据总体波动幅度明显降低;M估计法受到异常值的影响明显小于最小二乘法和递推最小二乘法。

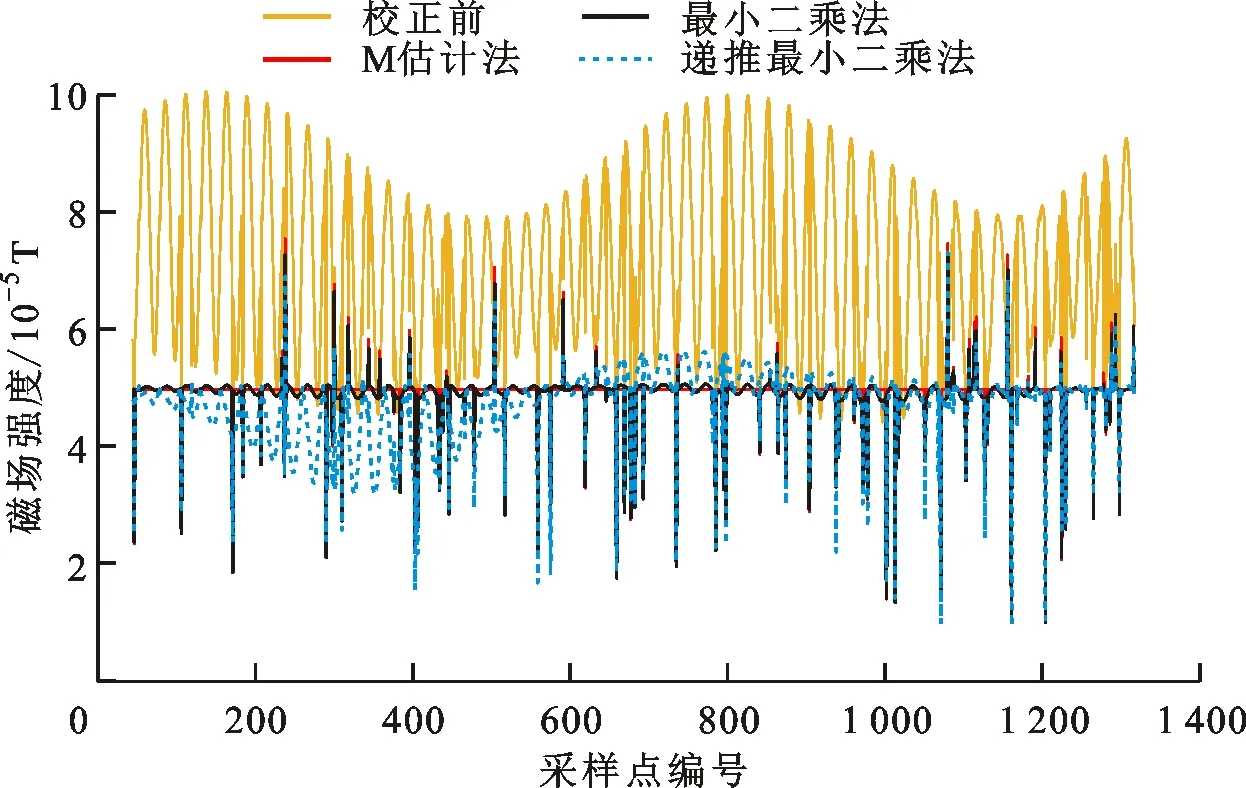
图3 补偿前后总磁场强度对比Fig.3 Comparison of total magnetic field intensity before and after compensation

在仿真中,3种算法去除异常测量值后的数据统计特性如表1所示。可以看出,M估计法的校正效果明显好于最小二乘法和递推最小二乘法的,M估计法有效降低了异常测量值对误差补偿的影响,提高了系统的鲁棒性。

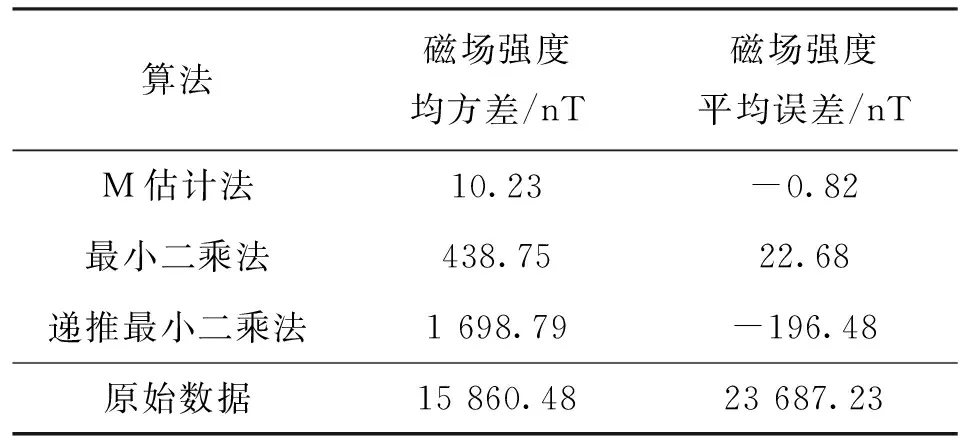
表1 仿真中3种算法的评估指标

4.2 实验验证

在南京某开阔地带进行地磁数据采集实验,使用美国Honeywell公司的HMR2300磁力计作为三轴磁传感器,如图4所示。将磁力计分别绕x、y、z轴旋转一周采集数据。对数据分别用最小二乘法和M估计法和递推最小二乘法进行椭球拟合,结果如图5所示。可以看出,采集的数据中包含了离群点,明显脱离椭球面,因此造成3种算法拟合的椭球面有明显差异。

图4 实验设备Fig.4 Experimental magnetometer

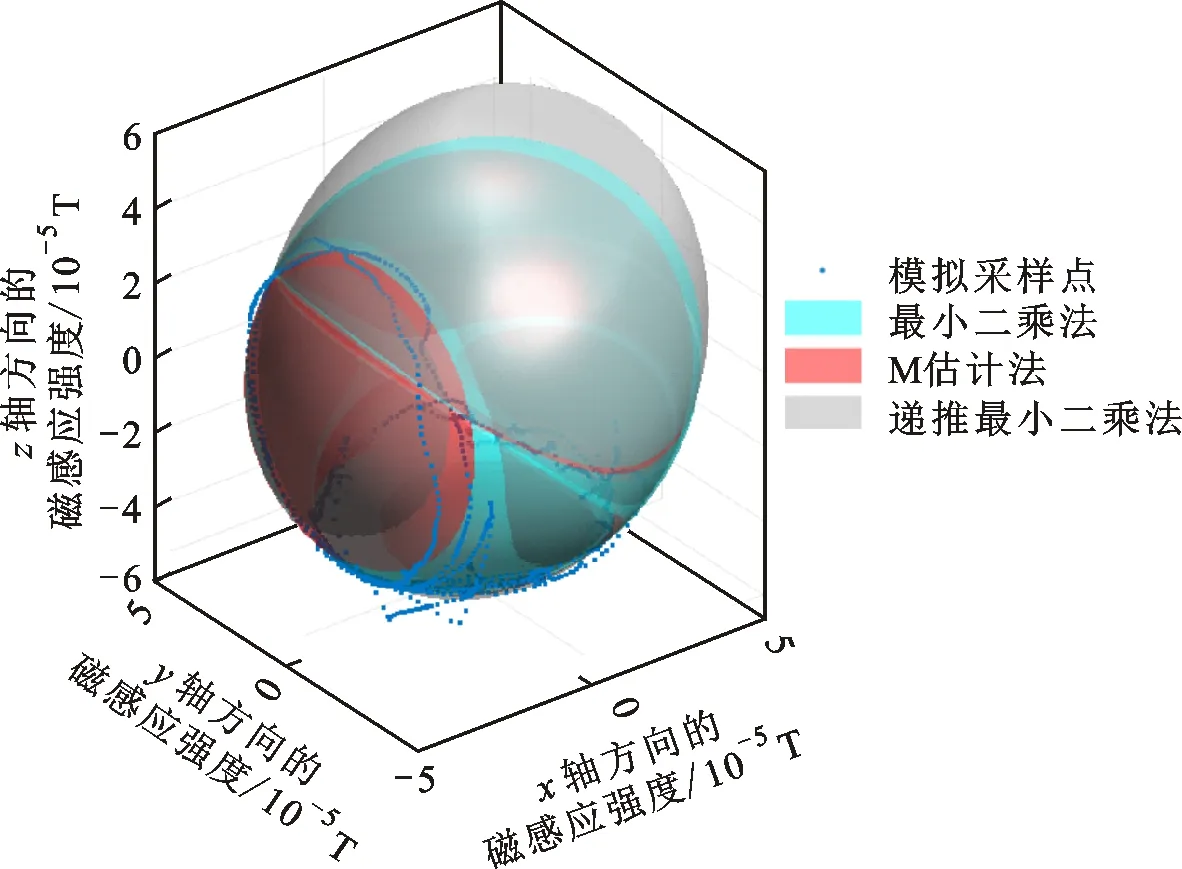
图5 拟合模型Fig.5 Fitting model

图6 3种补偿算法的总场强 Fig.6 Total field intensity of three algorithms for compensation

将校正前和3种算法校正后的三轴磁场数据转化为总磁场强度,结果如图6所示。可以看出,在第1 000个采样点附近,磁场强度发生明显波动,这可能是因为存在外界磁场干扰,因此造成采样出现异常值。本文认为单位化残差(Huber目标函数中的k)大于1.345的为异常值。

测量数据中去掉异常值后,各采样点与3种算法拟合椭球面的残差如图7所示。可以看出,M估计法残差波动明显小于最小二乘法和递推最小二乘法。

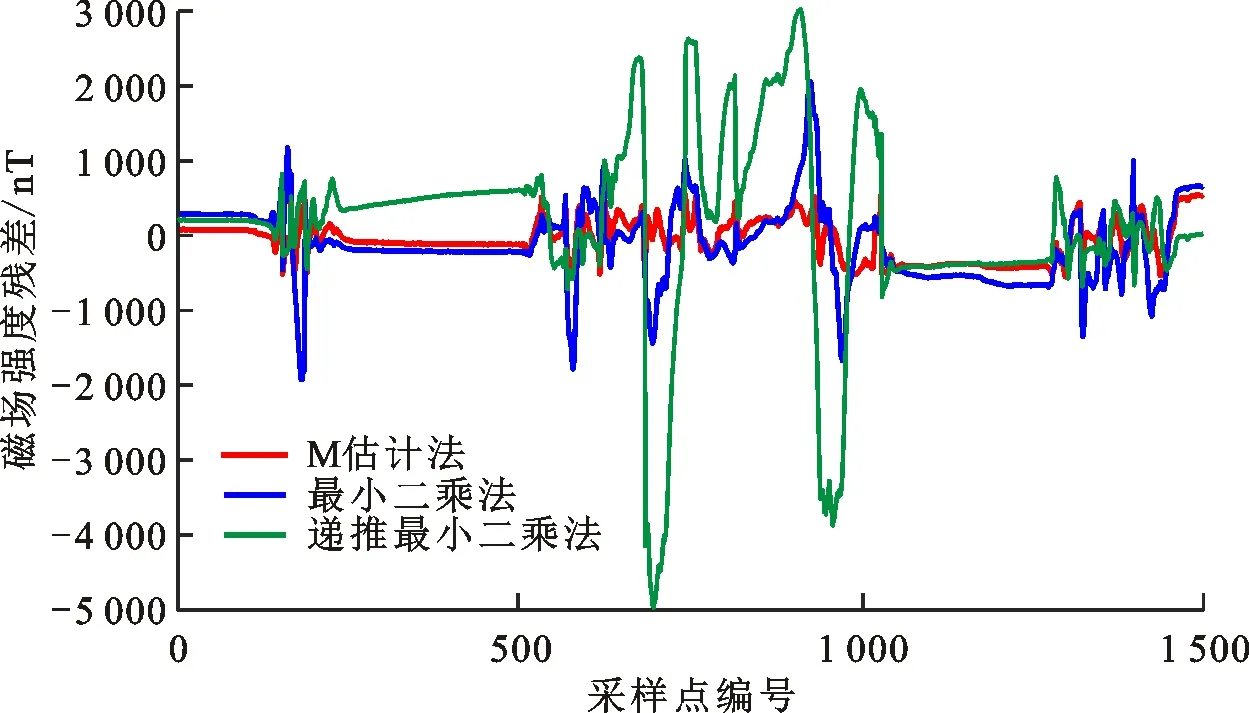
图7 实验中3种算法的拟合残差Fig.7 Residual error of the fitting results of three algorithms

在实验中,3种算法去除异常测量值后的数据统计特性如表2所示。M估计法的指标均优于传统最小二乘法和递推最小二乘法的,这表明M估计法有效克服了最小二乘法和递推最小二乘法对异常值敏感的缺点,抑制了磁测噪声,提高了系统鲁棒性。

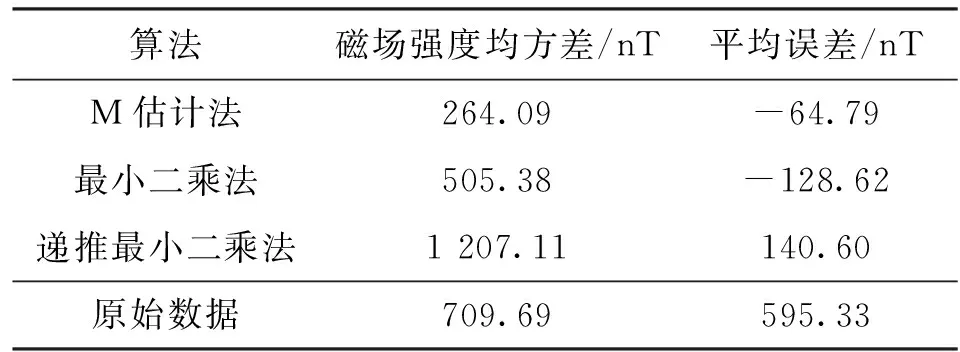
表2 实验中3种算法的评估指标

5 结 论

地磁测量误差校正是获取高精度真实地磁数据的关键。但是,之前的误差校正算法多假设数据采集过程中无异常点的出现。因此,本文提出了一种M估计补充策略下的三轴磁传感器误差的补偿算法,能够降低异常点对拟合的影响,提高地磁测量的精度。首先,分析了地磁测量中各种误差源,建立了磁传感器误差模型;其次,利用最小二乘法拟合椭球的参数;然后,在最小二乘法的基础上引入了M估计法对椭球参数进行迭代更新;最终,求取校准矩阵和偏移矢量,完成误差补偿过程。仿真结果表明,M估计法优于最小二乘法和递推最小二乘法。实验结果表明,用M估计补偿获得的数据均方差比使用递推最小二乘法的低78.12%,比使用最小二乘法的低47.74%。M估计在评估指标方面均优于传统的最小二乘法和递推最小二乘法,体现出较好的鲁棒性,具有很好的工程应用前景。