双鞍型天线与螺旋波等离子体的耦合距离对功率沉积的影响

李 帅,乔冠瑾,杜 丹*,杨开建,潘光祖,周 华

(1.南华大学 数理学院,湖南 衡阳 421001;2.南华大学 电气工程学院,湖南 衡阳 421001; 3.南华大学 核科学技术学院,湖南 衡阳 421001)

0 引 言

螺旋波是一种在哨声波频率范围内(离子回旋频率和电子回旋频率之间)，有着左右旋圆极化的边界波。使用螺旋波电离可以产生高密度的等离子体，螺旋波等离子体因其高电离率、高密度、均匀平稳、粒子能量可控等优点,广泛应用于薄膜沉积、等离子体火箭推进、半导体刻蚀和核聚变等领域[1-3]。

1970年，R.W.Boswell首次用一种新型天线(Boswell天线)制造了一种小型螺旋放电实验[4]。在这次实验中，测量到了高达3×1019m-3的极高的等离子体密度，在等离子体中心附近出现一个亮蓝色的区域。自此以后，人们对螺旋波等离子体相关理论不断深入，也进行了大量的实验，然而电离、功率沉积等机制已被所有研究者视为理解螺旋波等离子体的一个巨大难题，其中的各种物理机理仍在不断揭晓。1994～1998年，K.P.Shamrai[5-7]等人发现在螺旋波放电能量沉积过程中,存在着螺旋波之外的一种静电性质的表面波Trivelpiece-Gould(TG)波。射频功率主要通过两个通道传输到等离子体中：第一种通道是通过天线激发的弱阻尼螺旋波(H波)实现等离子体加热，第二种通道是在一定条件下，螺旋波在离子体表面附近与TG波进行模式耦合而将能量沉积入等离子体中。1998年,Y.Mouzouris[8]理论模拟表明调节磁场大小可控制H波和TG波在等离子体中的功率沉积分布：在低磁场情形下主要是TG波沉积在等离子体与真空边界处,而在高磁场情形下螺旋波在等离子体中心处主导能量沉积。2016年,S.Isayama等[9]研究得到碰撞频率极小时,等离子体中的功率沉积主要是由等离子体内部模式转换层(mode conversion surface，MCS)处螺旋波转换成TG波引起的。

国内，成玉国[10]研究了螺旋天线加热时磁场对TG波沉积在等离子体中的位置的影响。杜丹等[3]研究了双鞍型天线在仿星器H1等离子体中激发H波和TG波的条件，以及不同等离子体密度条件下H波和TG波的功率沉积。李文秋[2]等发现在不同电子温度范围内，TG波朗道阻尼和碰撞阻尼致使的能量沉积随电子温度改变。平兰兰[1]采用HELIC代码分析了HPPX装置中Half helix型天线、Nagoya III型天线和Boswell型天线的长度及运行频率对功率沉积的影响。双鞍型天线与等离子体的耦合距离能否控制H波和TG波在等离子体中的功率沉积分布？控制的程度有多大？这类问题的研究很少有人讨论过。本文采用自主编写程序研究了双鞍型天线与螺旋波等离子体的相互作用，分析了双鞍型天线与等离子体的耦合距离对H波和TG波在等离子体中的功率沉积分布的影响。

1 理论模型

双鞍型天线与螺旋波等离子体相互作用的示意图如图1所示。半径为rp，长度为L的柱状等离子体放置在z轴方向均匀分布的磁场B0中，等离子体放电的工质气体为氩气，双鞍型天线放置在轴向a0=L/2处，且到等离子体中心的距离为ra。柱形装置上下底面的两个金属平面分别位于z=0和z=L处，装置金属外壁到等离子体中心的距离为rb。

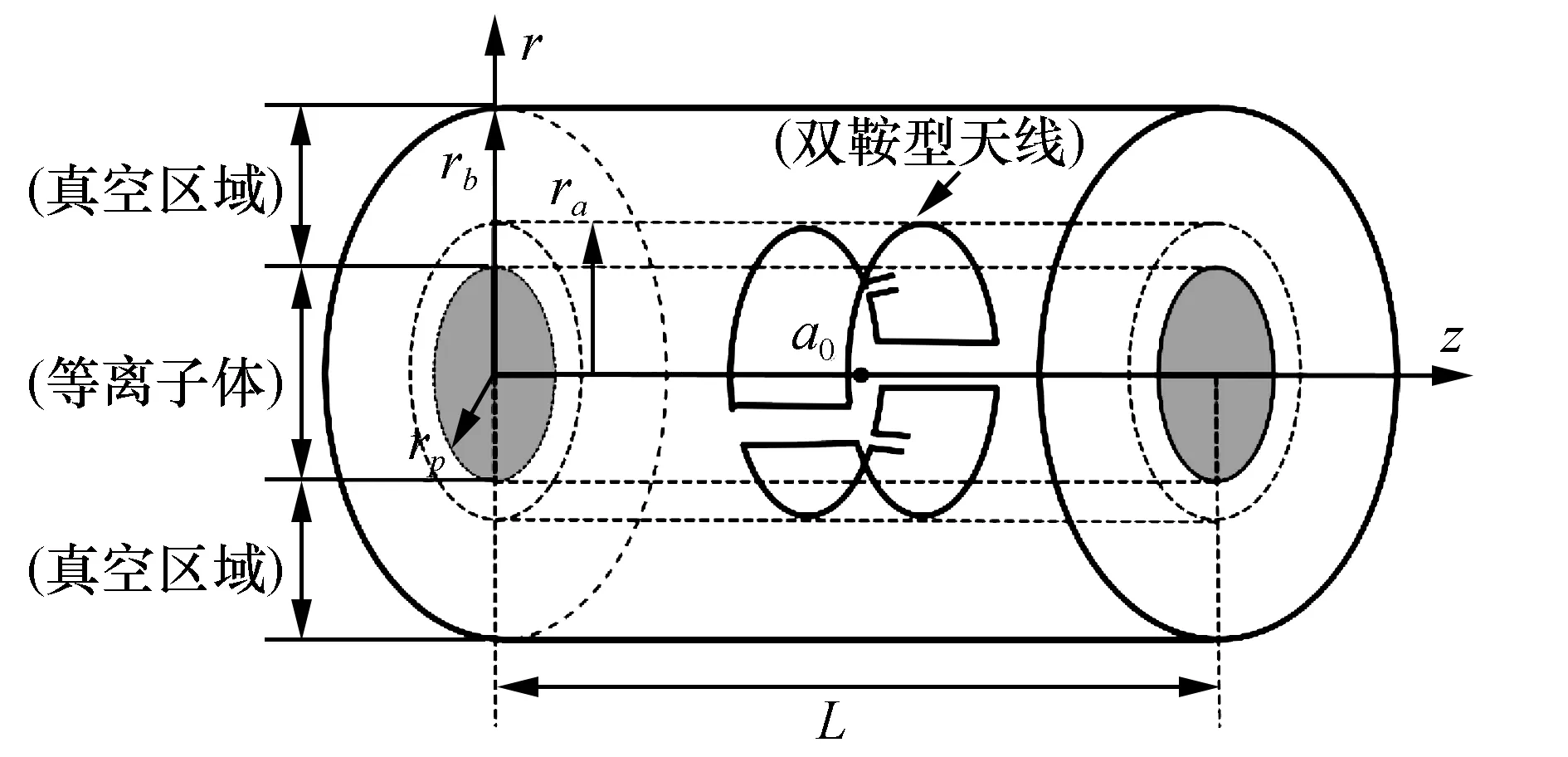
图1 双鞍型天线与螺旋波等离子体相互作用的示意图Fig.1 Schematic diagram of interaction between the double-saddle antenna and helicon wave plasma

为了研究双鞍型天线与螺旋波等离子体耦合到等离子体中的功率沉积,从麦克斯韦方程出发,得到电场E和磁场B满足的法拉第定律和安培定律:

(1)

(2)

在螺旋波天线激发的低温等离子体中，等离子体可假设是线性介质，电磁场的扰动以exp[i(kz+mφ+ωt)]形式变化[11]，其中ω=2πf是双鞍型天线的圆频率。根据Maxwell方程组(高斯制)，圆柱坐标(r,φ,z)中的电磁场和双鞍型天线的电流密度J满足的关系为[12]：

(3)

(4)

(5)

(6)

(7)

(8)

其中ε1,ε2,ε3为冷等离子体介电张量分量，Eφ=-iEθ，Bφ=iBθ，ρ=ωr/c,满足如下关系[12]：

(9)

(10)

(11)

下标i，e分别代表离子和电子，则υj，ωcj，ωpj分别对应不同粒子的碰撞频率，回旋频率及等离子体频率。

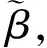
图2 双鞍型天线模型Fig.2 The model of the double-saddle antenna

当θ>0时：

(12)

θ<0时，Jθ(r,-θ,z)=-Jθ(r,θ,z)，

(13)

(14)

对于均匀等离子体，整理麦克斯韦方程组(3)～(8)，可得[13]：

(15)

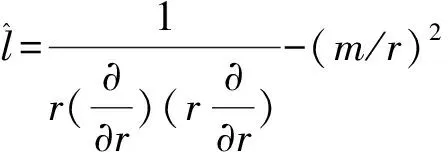
(16)

其中

β=ε3(1-N2/ε1)，

γ=N2ε2ε3/ε1，

δ=Nε2/ε1。

等离子体中的电场和磁场定义如下：

Ez(ρ)=a1e1(ρ)+a2e2(ρ)

(17)

Bz(ρ)=a1b1(ρ)+a2b2(ρ)

(18)

Eφ(ρ)=a1E1(ρ)+a2E2(ρ)

(19)

Bφ(ρ)=a1B1(ρ)+a2B2(ρ)

(20)

式中

ρ=rω/c，

bj=Jm(pjρ)，

F=ε1-N2，

由式(3)，式(6)可得电磁场径向分量：

(21)

(22)

双鞍型天线与等离子体相互作用时，电磁场满足如下边界条件：

(23)

(24)

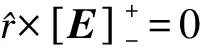
(25)

(26)

(27)

真空中ε1=ε3=1,ε2=0,则电场和磁场为：

(28)

(29)

式中

f(ρ)=ρb[Km(κρb)Im(κρ)-Im(κρb)Km(κρ)]

g(ρ)=ρa[Km(κρa)Im(κρ)-Im(κρa)Km(κρ)]

上述方程中，Im，Km是第m阶修正贝塞尔函数，角标a，b，p分别表示函数在ra，rb，rp处取的值。

方程(15)联立边界条件(23)～(27)，就可以求出方程(17)～(20)的系数a1，a2。再将方程(17)～(20)、(28)～(29)、(23)～(27)联立即可得到等离子体和真空区域的电磁场分布。

等离子体局部功率沉积为

(30)

其中

(31)

总功率沉积

(32)

2 数值计算与结果分析

采用Fortran语言编写程序HWAP模拟任意形状的天线与均匀螺旋波等离子体的耦合、传播和吸收过程。为了验证程序，取文献[12]中的参数模拟了Boswell天线与螺旋波等离子体相互作用时m=1,l=2模式波的电场Ez的径向分布图(如图3所示)。从图3(a)和图3(b)的对比可知，程序HWAP的模拟结果与文献[12]的基本一致，程序的准确性得到验证。

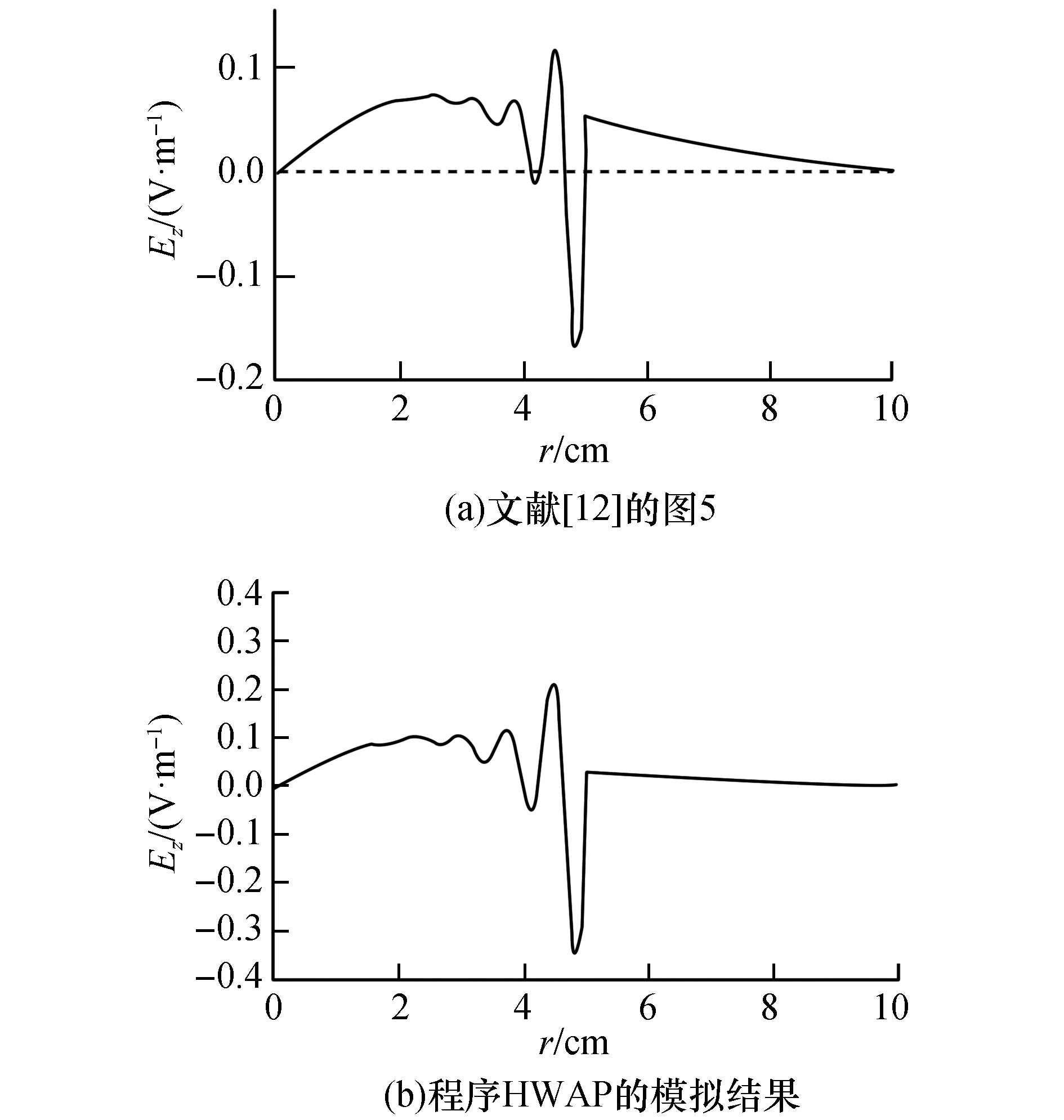
图3 m=1,l=2模式波的电场Ez的径向分布图Fig.3 Schematic diagram of the radial profiles of Ez for m=1, l=2 mode

图4 等离子体z=157 cm处场Br和Er的径向分布图Fig.4 Radial field structure Br and Er at z=157 cm

图5模拟了ra=18.5 cm、20.5 cm和22.5 cm时波在等离子体中的局部功率沉积Pabs的径向分布图。从图4和5可知，螺旋波和TG波在ra=17.0 cm处进行模式耦合，转换的TG波主要沉积在等离子体边界处(17.0 cm

图5 ra=18.5 cm、20.5 cm、22.5 cm时的 局部功率沉积Pabs的径向分布Fig.5 Radial distribution of local power deposition Pabs for ra=18.5 cm,20.5 cm,22.5 cm

图6模拟了螺旋波在等离子体中沉积的总功率Qr,H，TG波在等离子体中沉积的总功率Qr,TG，以及螺旋波和TG波在等离子体中沉积的总功率Qr,TG+H随天线耦合距离ra变化的曲线图。从图6可知，改变天线到等离子体中心的距离ra可以改变螺旋波和TG波在波能量沉积过程中起的主导作用和总的功率沉积大小：等离子体中螺旋波的功率沉积随耦合距离ra的增加而减少，16.4 cm

图6 总功率沉积Qr,TG+H、Qr,TG、Qr,H 随天线耦合距离ra的变化关系Fig.6 The relationships between the total energy deposition of Qr,TG+H、Qr,TG、Qr,H and the antenna coupling distance ra

3 结 论

本文采用自主编写的程序HWAP模拟了双鞍型天线与均匀螺旋波等离子体相互作用时耦合距离对功率沉积的影响。模拟结果表明：1)在一定实验条件下，双鞍型天线发射的波在等离子体中同时激发螺旋波和TG波，控制天线与等离子体的耦合距离可改变TG波在等离子体边界附近的能量沉积分布；2)双鞍型天线的耦合距离的变化可改变螺旋波和TG波在能量沉积过程中起的主导作用，在一定耦合距离范围内(如16.4 cm