三维最小二乘弹性高斯束叠前深度偏移

孙昌潇， 毛伟建， 张庆臣， 石星辰

1 中国科学院精密测量科学与技术创新研究院计算与勘探地球物理研究中心； 大地测量与地球动力学国家重点实验室， 武汉 430077 2 中国科学院大学， 北京 100049

0 引言

地震叠前深度偏移成像是揭示地下油气藏构造信息的关键技术，传统的偏移方法通过求解正演算子的伴随算子，将地表接收点采集到的时间域地震波场反传到地下来获得散射点的位置.由于偏移算子不是正演算子的逆，并且受到采集系统局限、深部地层构造复杂、实际地震数据通常伴有噪声等因素的影响，传统的偏移方法通常只能得到一个模糊的成像，分辨率较低.反演是获取地下物性参数的重要手段，并且随着计算机技术的飞速发展，反演正在越来越多地应用到地震数据处理中，能够为地震资料解释提供强有力的证据.最小二乘偏移联合偏移和反演，依据线性化反演的思路(Tarantola，1984)，将成像作为一个反问题进行求解，在最小二乘目标函数约束下，修正偏移成像的振幅，反演地层真实的反射信息.

Nemeth等(1999)提出最小二乘偏移成像方法，用于减少成像中采集脚印的影响和迭代恢复缺失地震数据.随后，最小二乘偏移得到了国内外地球物理学家广泛的研究和应用.通过在同样观测系统下模拟数据与实际观测数据的迭代更新拟合，最小二乘偏移可以解决传统构造成像分辨率低、照明不均衡的问题(Chavent and Plessix，1999；Duquet et al.，2000；Aoki and Schuster，2009；Dai and Schuster，2013；马方正等，2016)，同时可以压制成像串扰(Dai et al.，2011，2012；刘玉金等，2013；Dutta，2017；Zhang et al.，2019；张攀和毛伟建，2018).但是最小二乘偏移往往需要几十次迭代，每次迭代都包含一次从震源到地下散射点的正向传播，和一次来自接收点位置的反向传播，计算时间是传统偏移方法的2n(n为迭代次数)倍，因此大量的计算耗时是需要解决的问题.

高斯束偏移基于高斯束模拟非奇异、振幅处处正则的地震波场，是一种灵活、准确、高效的深度域偏移成像方法.它兼具射线类和波动方程类偏移成像的优势，能够解决两点射线追踪存在的多路径的问题(Hill，1990，2001；Gray，2005；Gray and Bleistein，2009)，适用于三维复杂地质构造的成像.20世纪90年代初，Hill(1990)提出高斯束偏移成像的思路，给出了高斯束的计算公式，以及基于高斯束叠加的波场延拓公式，用于叠后偏移.在此之后，高斯束偏移经历了从叠后到叠前、2D到3D、声波均匀各向同性介质到复杂各向异性介质中的高斯束偏移(Popov et al.，2010 ；Protasov，2015；Li et al.，2018；Yang et al.，2018b).最小二乘高斯束偏移结合最小二乘和高斯束偏移成像的优势，能够提高成像分辨率，均衡成像振幅(Hu et al.，2016；Yuan et al.，2017).Yang等(2018a)提出时间域最小二乘高斯束偏移成像的方法，推导了时间域高斯束Born正演公式和偏移公式，并且运用正则化约束方法增强反演的稳定性.Yue等(2019)将最小二乘高斯束偏移方法应用到二维弹性介质成像，提高了PP和PS波成像的分辨率.目前最小二乘高斯束偏移的相关研究与讨论较少，并且还未涉及三维介质中最小二乘高斯束偏移的应用.最小二乘高斯束偏移具有灵活度高、计算效率快等优势，因此该方法值得我们研究和开发.

本文提出了一种最小二乘弹性高斯束偏移成像方法，并把它应用于三维弹性波成像.首先，在炮点和检波点附近稀疏位置分别向下进行基于高斯束叠加表示的多波型波场延拓，三维空间下表达为P波、S1波和S2波三种波型的波场延拓形式.然后根据高斯束的走时和振幅信息，将三维地下介质的扰动点能量映射到地表稀疏位置并得到多波型局部平面波.利用不同的应力边界条件下，多波和多分量地震记录之间的关系，构建波型波矢量转换矩阵(栗学磊和毛伟建，2016)，合成多分量局部平面波.然后在地表划分一系列重叠排列的高斯窗，应用局部逆倾斜叠加公式(岳玉波等，2019a，2019b)，在接收点合成多分量地震记录.偏移算子取Born正演(反偏移)算子的伴随算子，采用共轭梯度算法更新成像结果来拟合反偏移数据与实际观测数据，使成像振幅逐渐趋近于地下真实的反射系数，从而提高偏移成像的分辨率，增强地下照明.本文通过构建的波型波矢量转换矩阵来进行每次迭代过程中多波型、多分量局部平面波之间的转换，从而降低最小二乘偏移PP和PS成像串扰.为了更好地平衡PP和PS偏移反演的结果，我们在反演过程中分别控制修正PP和PS成像的步长，使迭代过程稳定收敛.通过模型测试表明，最小二乘弹性高斯束偏移方法能够有效提高成像分辨率.复杂Marmousi2模型的测试结果表明对于陡倾角构造和深层射线覆盖率低、成像振幅弱的区域，最小二乘弹性高斯束偏移可以提高成像保幅能力.从三维弹性波成像的纵向剖面和横向截面上看，最小二乘弹性高斯束偏移能够得到更为清晰的成像结果.

1 工作原理

1.1 弹性高斯束Born正演

根据一阶Born近似模拟散射波场的理论(Beylkin and Burridege，1990；Bleistein et al.，2001)，在弹性介质中，由震源s激发，经地下介质传播到r处接收的vr波型弹性波场uvr(r,s,ω)表示为

(1)

定义激发震源为爆炸源，因此vs代表P波型，vr代表P、S1或S2波型(栗学磊和毛伟建，2016)；S(ω)为频率域震源函数；M(x)表示x点的反射率，它与介质的弹性参数有关；格林函数Gvsvr(r,s,ω)表示在地表r位置接收到的由s位置激发vs波型单位源的响应.将公式(1)中Gvsvr(r,s,ω)表示为Gvs(x,s,ω)Gvr(r,x,ω)的形式，并且根据互易性定理Gvr(r,x,ω)=Gvr(x,r,ω)，公式(1)弹性波场uvr(r,s,ω)的表达式变为

(2)

因此，一阶Born正演弹性波场表达为震源到地下散射点的格林函数、检波点位置处接收的格林函数、频率域震源函数，以及反射率在频率域的积分.

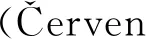
弹性高斯束Born正演的格林函数表示为弹性高斯束叠加的形式(Hill，2001)：

(3)

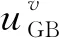
高斯束Born正演过程是将地下散射点能量映射到地表合成局部平面波，再在地表划分一系列重叠排列的高斯窗，将(p,ω)域数据变换到(r,ω)域，该过程可以看作局部倾斜叠加的逆过程.Hill(2001)给出了高斯窗划分的归一化表达式：

(4)

其中，常数a表示相邻两个高斯束的间隔，ωl和wl分别表示参考频率和初始束宽度.将公式(4)代入弹性高斯束叠加表示的检波点格林函数Gvr(x,r,ω)中，并且引入相移校正因子exp[-iωp·(r-L)]，则

(5)

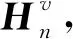
(6)

(7)

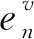
将公式(5)、(6)代入一阶Born近似公式(2)中，并且将震源格林函数也表达为弹性高斯束叠加的形式，则震源s点激发地震波场，到r处接收的弹性波矢量场un(r,s,ω)的表达式为

其中Dvr(L,s,p,ω)表示地表稀疏高斯束中心位置合成的vr波型局部平面波，具体表达式如下：

(9)

1.2 最小二乘弹性高斯束偏移

最小二乘偏移的本质在于运用偏移的手段，通过接收点采集到的地震记录反演背景地球物理模型下未知散射点或扰动点的值，其中重要的环节是计算高斯束Born正演(反偏移)算子和它的伴随算子，即高斯束偏移算子.对一阶Born近似正演过程求共轭转置，偏移过程表示为

(10)

Gvs*(x,s,ω)、Gvr*(x,r,ω)和S*(ω)分别表示震源格林函数、检波点格林函数和震源函数的复数共轭.格林函数表示为弹性高斯束叠加的形式，则

(11)

(12)

假定l表示弹性高斯束Born正演(反偏移)算子，弹性高斯束偏移算子用lT表示，则弹性高斯束反偏移过程可以用算子l作用于地下介质扰动模型m的形式表示.依照线性化反演的思路，构建最小二乘框架下的目标函数：

φ(m)=‖d-lm‖2，

(13)

式中，d表示地表接收点采集到的实际地震数据.因此，最小二乘偏移的目的在于通过正演模拟地震数据来拟合实际的观测地震数据.上式中，令∂φ(m)/∂m=0，整理得到

m=(lTl)-1lTd，

(14)

其中，lTl称为Hessian矩阵.由于严格意义上求解Hessian矩阵计算量大、成本高，通常研究Hessian矩阵逆的近似作为预条件，来帮助反演地下介质的反射率(Guitton，2004；Tang，2009；Ayeni and Biondi，2010；任浩然等，2013).

1.3 共轭梯度反演算法

用梯度导向的迭代算法求解目标函数：

mk+1=mk+αgk+1，

(15)

其中，k表示迭代次数；α表示步长；gk+1表示第k+1次迭代的目标梯度；mk和mk+1分别表示第k次和第k+1次反演的地下介质扰动，在最小二乘弹性高斯束偏移成像中，mk和mk+1表示第k次和第k+1次迭代的PP和PS成像结果.从表达式中可以得出，反演的准确性是依据模拟数据与实际观测数据的拟合程度来判定.

共轭梯度算法通过加入一个对梯度的修正，使反演过程更加稳定收敛.假设初始模型m0=0，第一次迭代的成像结果m1=αlTd，相当于对观测数据做一次偏移成像.第k+1(k=1，2，3…)次迭代得到偏移成像mk+1的计算流程如下：

(16)

其中sk+1和β分别表示第k+1次迭代的共轭梯度和它的步长.

最小二乘弹性高斯束偏移需要同时反演PP和PS成像，在数据域表现为多分量地震数据的拟合.为了更好地控制PP和PS成像反演的速率和下降方向，本文采用了一种分别拟合PP成像和PS成像反偏移多分量模拟数据与实际多分量观测数据的方法.在每次迭代过程中，分别控制PP和PS成像修正的步长，记作αPP和αPS，该方法使PP和PS成像反演更稳定.

2 模型试算

为了验证最小二乘弹性高斯束偏移成像方法的有效性，分别采用二维凹陷、Marmousi2模型以及三维SEG/EAGE Salt模型进行测试，实际地震数据通过有限差分方法正演得到.分别对比了传统弹性高斯束偏移方法和最小二乘弹性高斯束偏移方法的成像结果，并且分析了成像频谱变化和目标函数的收敛情况.

2.1 2D凹陷模型

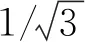
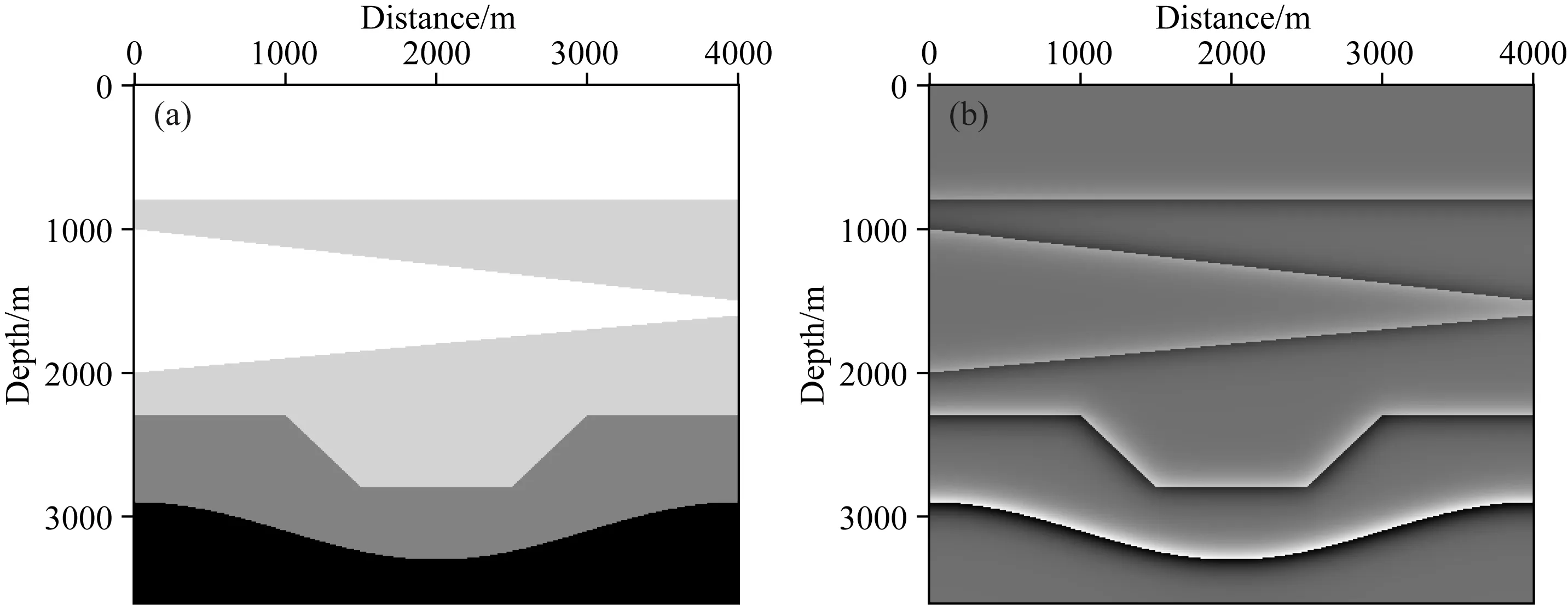
图1 凹陷模型(a) P波速度； (b) PP反射率.Fig.1 The sunken model(a) P wave velocity； (b) PP reflectivity.

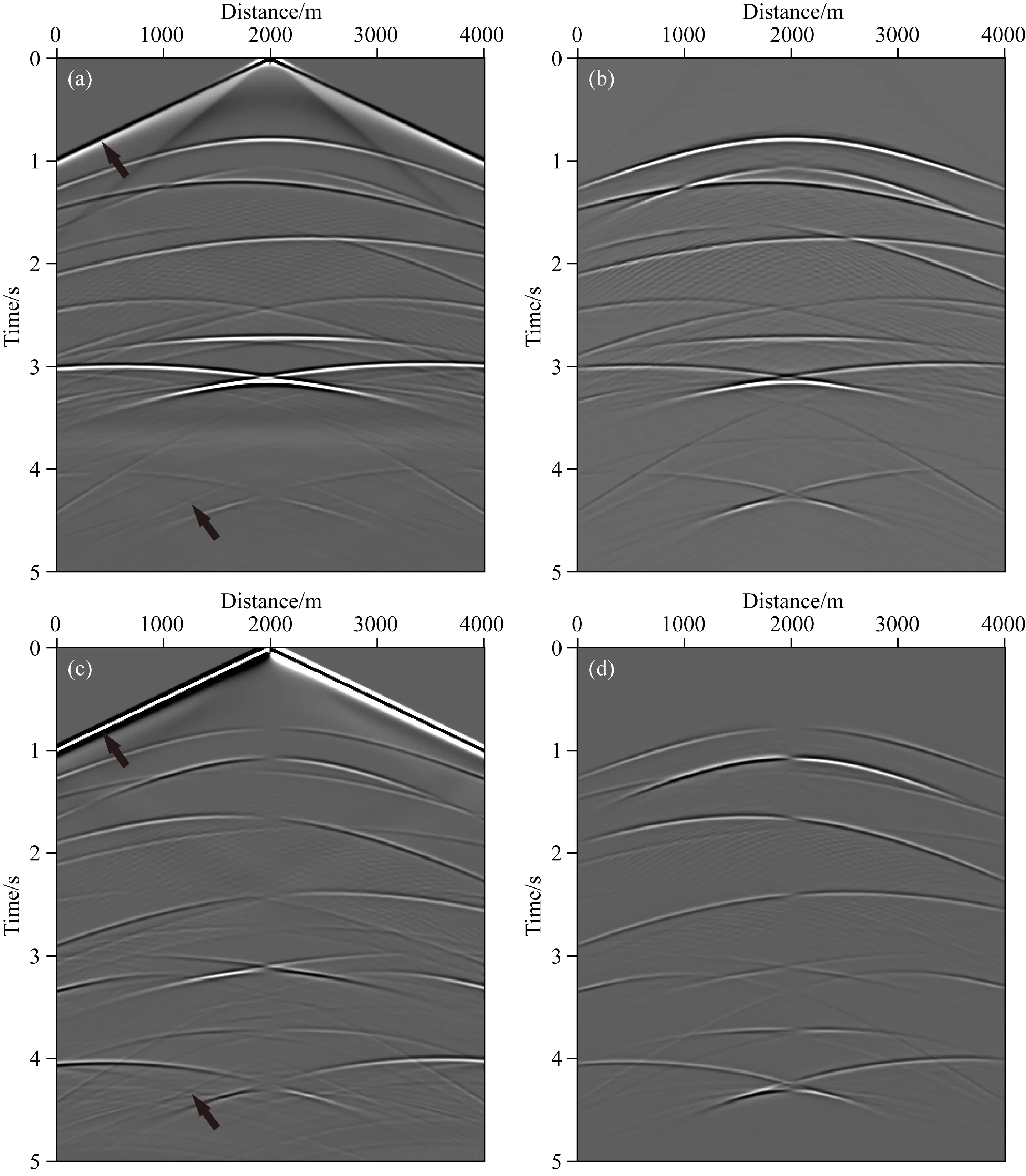
图2 不同方法正演的单炮地震记录有限差分正演z分量(a)、x分量(c)数据；弹性高斯束Born正演z分量(b)、x分量(d)数据.Fig.2 The synthetic data using different modeling methodsz-component (a) and x-component (c) data using finite difference forward modeling method；z-component (b) and x-component (d) data using elastic Gaussian beam Born modeling method.

图3表示传统的弹性高斯束偏移成像与最小二乘弹性高斯束偏移成像的对比结果.如该图显示，传统弹性高斯束偏移PP和PS成像(图3a、3c)的分辨率较低，照明不均衡，并且由于观测系统的局限性，凹陷两侧倾斜断层构造的射线覆盖率低，成像振幅比较弱. 10次迭代后最小二乘弹性高斯束偏移PP、PS成像如图3b、3d所示，结果表明，最小二乘偏移成像的分辨率有了明显的提高，地下照明不足或者照明不到的地方也得到了一定的补偿，断层构造地区的成像振幅得到增强.

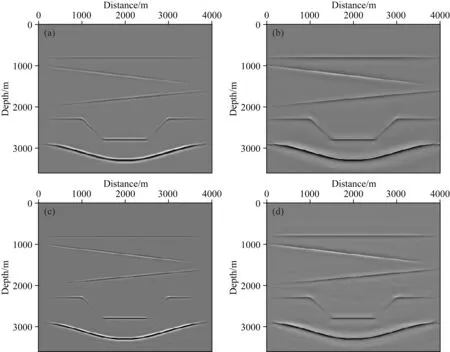
图3 (a)和(c)是传统弹性高斯束PP和PS波偏移结果，(b)和(d)是最小二乘弹性高斯束PP和PS波偏移结果Fig.3 (a) and (c) are conventional elastic Gaussian beam migration results for PP and PS waves;(b) and (d) least-squares elastic Gaussian beam migration results for PP and PS waves

图4表示同一个尺度范围下显示的观测数据与反偏移模拟数据残差，1次迭代和10次迭代后的z分量数据残差如图4a、4b所示，x分量数据残差如图4c、4d所示.从图中可以看出，迭代10次后x分量和z分量的数据残差都明显减小.图4b、4d中显示仍然有很小一部分数据残差未随着迭代次数的增加而减小，这是因为反偏移无法合成超过射线覆盖范围以外的地震记录.为了进一步比较目标函数随迭代次数的收敛情况，我们给出随迭代次数增加的归一化目标函数收敛曲线，如图5.经过10次迭代后，目标函数收敛为第1次迭代的20%左右.

图4 观测和模拟单炮地震记录的残差1次迭代后z分量(a)、x分量(c)的数据残差；10次迭代后z分量(b)、x分量(d)的数据残差.Fig.4 The data residuals between simulated and observed dataz-component (a) and x-component (c) residuals at the 1st iteration；z-component (b) and x-component (d) residuals at the 10th iteration.

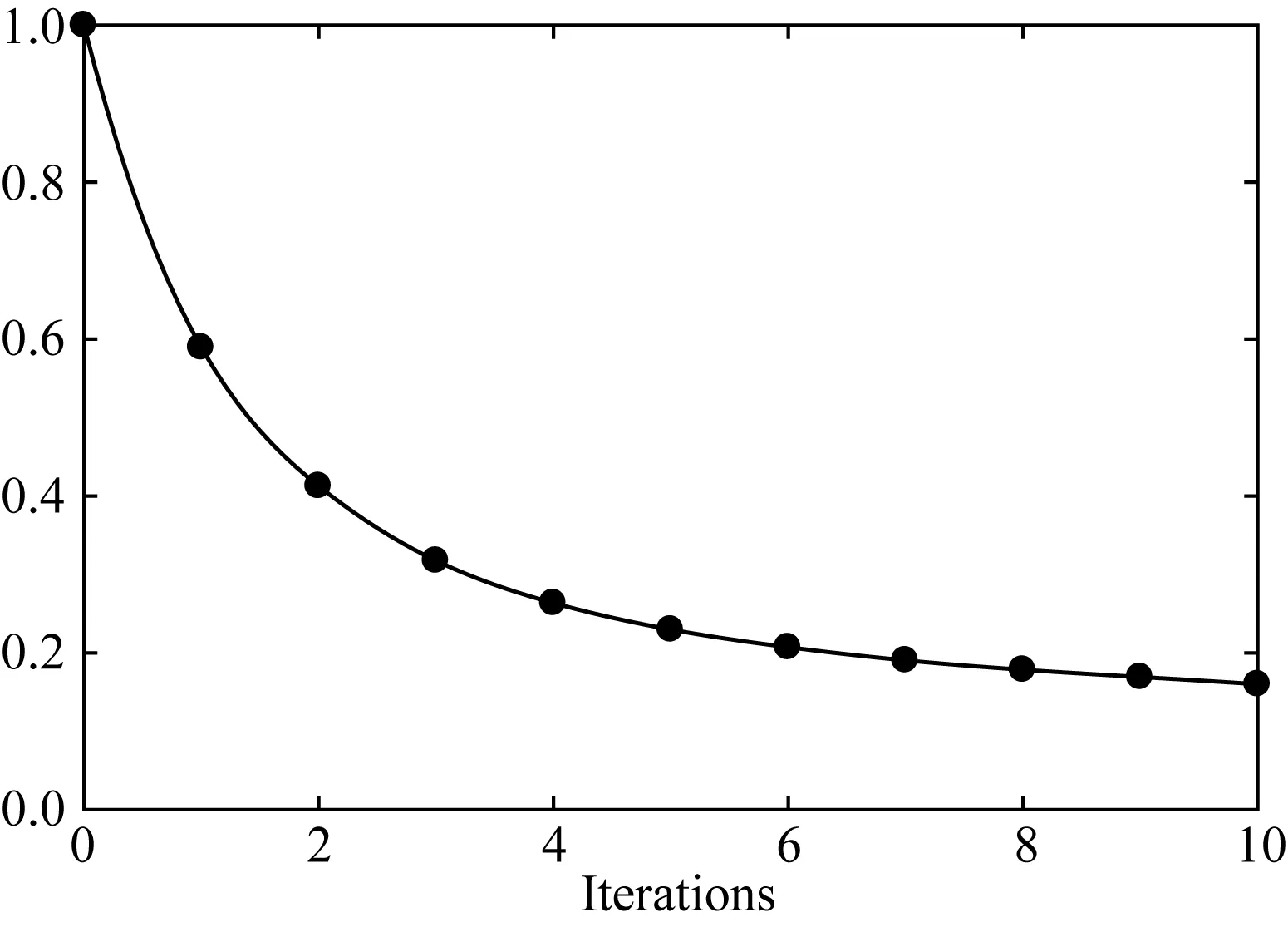
图5 归一化的目标函数收敛曲线Fig.5 The convergence curve of the normalized objective function

2.2 2D Marmousi2模型

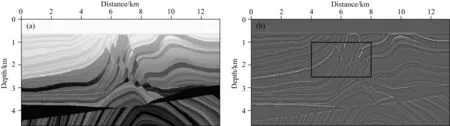
图6 Marmousi2模型(a) P波速度； (b) PP反射率.Fig.6 The Marmousi2 model(a) P wave velocity； (b) PP reflectivity.

图7中分别给出了传统弹性高斯束偏移PP(图7a)和PS(图7c)成像剖面以及10次迭代后的最小二乘弹性高斯束偏移PP(图7b)和PS(图7d)成像剖面.从图中可以观察到，传统偏移方法得到的PP成像剖面照明不均衡，特别是在地层深部和地层结构变化剧烈的区域，照明度明显地削弱，并且成像分辨率低，即使PS成像的分辨率比PP成像的分辨率要高，但也存在照明不均衡的问题.相比传统偏移PP和PS成像，最小二乘弹性高斯束偏移方法提高了PP和PS成像分辨率，并且能够一定程度上均衡地层照明，补偿深部弱信号，增强成像的保幅性.然而随着迭代次数的增加，最小二乘弹性高斯束偏移成像受到部分假象和噪声影响信噪比降低，这是因为目标函数解的非光滑性使得迭代后的成像结果常伴有一定的低频噪声.并且由于最小二乘偏移是一种线性化反演方法，复杂的地层构造增加了地震数据拟合的难度，进而一定程度上影响成像反演的稳定性.

图7 (a)和(c)是传统弹性高斯束PP和PS波偏移结果; (b)和(d)是最小二乘弹性高斯束PP和PS波偏移结果Fig.7 (a) and (c) are conventional elastic Gaussian beam migration results for PP and PS waves;(b) and (d) least-squares elastic Gaussian beam migration results for PP and PS waves

我们选取模型中结构变化剧烈的部分(图6b黑色方框所示)放大进行更清晰地对比分析.从图8虚线方框部分的成像效果来看，与传统弹性高斯束偏移相比，最小二乘弹性高斯束偏移方法的成像分辨率更高，地层结构更清晰.另外，在图中黑色箭头所指部分，由于地层结构复杂，传统的高斯束偏移不足以对该区域进行精确成像，而最小二乘弹性高斯束偏移能够补偿该区域的照明，提高成像的保幅性.

图8 图6b中黑色方框部分的偏移结果比较(a)、(b) PP、PS反射率； (c)、(d) 传统的弹性高斯束PP、PS偏移； (e)、(f) 最小二乘弹性高斯束PP、PS偏移.Fig.8 The comparison among the migration results in the black box of Fig.6b(a) and (b) PP and PS reflectivity； (c) and (d) Conventional elastic Gaussian beam migration for PP and PS images； (e) and (f) Least-squares elastic Gaussian beam migration for PP and PS images.

分别抽取传统弹性高斯束偏移和最小二乘弹性高斯束偏移成像剖面其中的一道，绘制单道频谱曲线，如图9a、9b所示.由于震源为Ricker子波，传统偏移成像的频谱范围有限，通过多次迭代，弹性高斯束最小二乘偏移PP和PS成像的频谱范围都得到一定的拓宽，进而说明迭代后的成像分辨率有所提高.

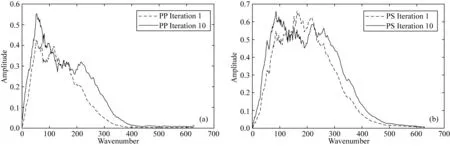
图9 1次迭代和10次迭代后PP、PS成像的频谱Fig.9 The spectrums of PP and PS images at the 1st and 10th iteration

2.3 3D弹性SEG/EAGE Salt模型

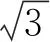
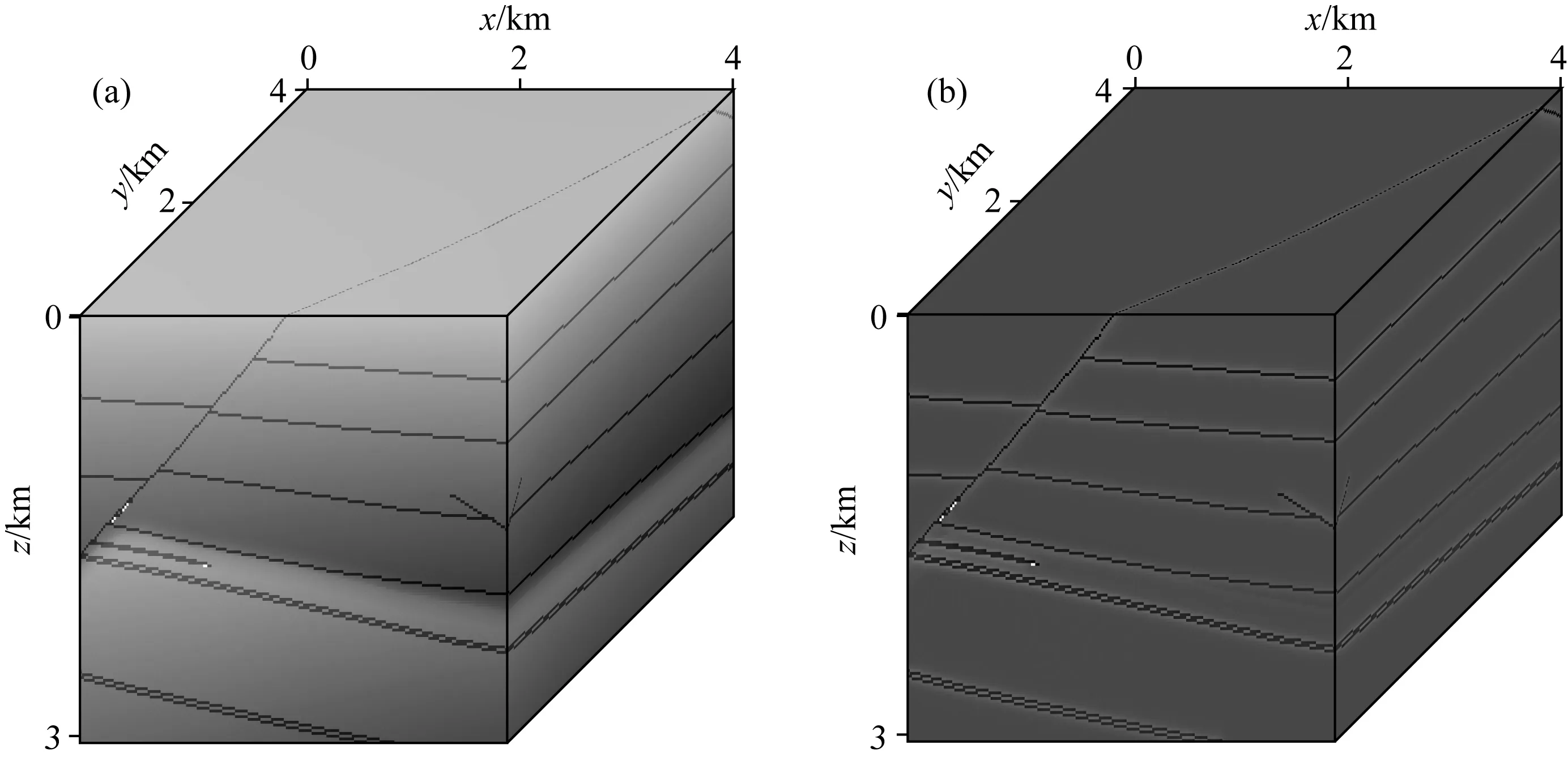
图10 截断SEG/EAGE Salt模型(a) P波速度； (b) PP反射率.Fig.10 The truncated SEG/EAGE Salt model(a) P wave velocity； (b) PP reflectivity.

图11 不同方法正演的三分量地震记录有限差分正演z分量(a)、x分量(b)、y分量(c)数据；弹性高斯束Born正演z分量(d)、x分量(e)、y分量(f)数据.Fig.11 The three-component data using different modeling methodsz-component (a)，x-component (b) and y-component (c) data using finite difference forward modeling method；z-component (d);x-component (e) and y-component (f) data using elastic Gaussian beam Born modeling method.

为了比较三维最小二乘弹性高斯束偏移PP、PS成像与传统弹性高斯束偏移PP、PS成像，图12给出三维偏移结果x=1.2 km、y=2 km、z=2.4 km上的成像切片.通过图中黑色箭头所指位置可以看出，相比传统高斯束偏移，迭代后的PP和PS成像的分辨率都有了明显地提高，深层照明也得到了补偿，并且更清晰地刻画出地层的特征.深度切片能够帮助我们了解地下介质的分布特征，图13展示了z=1.3 km处的深度切片.图13a、13c表示传统弹性高斯束偏移PP和PS的深度切片，图13b、13d表示最小二乘弹性高斯束偏移PP和PS的深度切片，如图所示，最小二乘弹性高斯束偏移深度切片的分辨率更高，照明范围更广.

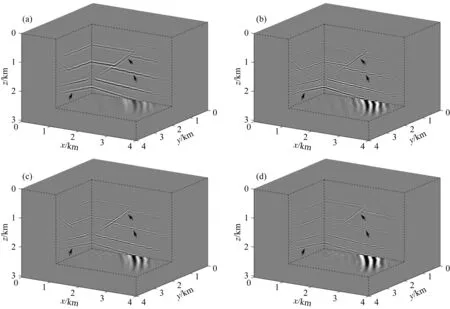
图12 (a)和(c)是传统弹性高斯束PP和PS波偏移结果，(b)和(d)是最小二乘弹性高斯束PP和PS波偏移结果Fig.12 (a) and (c) are conventional elastic Gaussian beam migration results for PP and PS waves; (b) and (d) least-squares elastic Gaussian beam migration results for PP and PS waves

图13 z=1.3 km切片上传统弹性高斯束PP和PS偏移(a、c)，最小二乘弹性高斯束PP和PS偏移(b、d)的成像结果Fig.13 Depth slice at z=1.3 km.(a) and (c) are conventional elastic Gaussian beam migration results for PP and PS waves; (b) and (d) least-squares elastic Gaussian beam migration results for PP and PS waves

分别作出y=2 km处传统弹性高斯束偏移和最小二乘弹性高斯束偏移PP、PS成像剖面的二维频谱，如图14所示.对比图14a、14c，PS成像的分辨率比PP成像的分辨率要高，频谱范围更广.分别比较图14a、14b和图14c、14d中方框所示部分，最小二乘弹性高斯束偏移方法一定程度上拓宽了PP和PS成像的频谱范围，因此可以证明，最小二乘弹性高斯束偏移方法可以提高成像分辨率.

图14 1次迭代(a、c)和10次迭代(b、d)后PP(a、b)和PS(c，d)波成像的二维频谱Fig.14 The 2D spectrums of images for PP (a，b) and PS (c，d) waves at the 1st (a，c) and 10th (b，d) iteration

对比图15给出的1次迭代和10次迭代后三分量反偏移模拟数据与观测数据残差可知，地震记录残差中的绝大部分一次反射波经过迭代后收敛.我们在最小二乘弹性高斯束偏移之前对数据进行了去直达波处理，但仍存在部分残余的直达波，这部分直达波残差在迭代过程中未收敛.由于地层构造复杂，存在高斯束无法完全覆盖的区域，因此反偏移也无法模拟该部分正演的地震波.

图15 观测和模拟单炮地震记录的残差1次迭代后z分量(a)、x分量(b)、y分量(c)的数据残差；10次迭代后z分量(d)、x分量(e)、y分量(f)的数据残差.Fig.15 The data residuals between simulated and observed data. z-component (a)，x-component (b) and y-component (c) residuals at the 1st iteration；z-component (d); x-component (e) and y-component (f) residuals at the 10th iteration

3 结论

本文推导了弹性高斯束Born正演(反偏移)模拟多分量地震记录的公式，通过在数据域进行反偏移模拟数据与实际观测数据的拟合实现最小二乘意义下的三维弹性高斯束偏移成像，并采用共轭梯度法迭代修正偏移成像振幅.本文提出在每次偏移和反偏移迭代过程中通过构建波型波矢量转换矩阵完成多波型、多分量局部平面波之间的转换，从而降低最小二乘偏移PP和PS成像串扰，并且提高反演效率.为了更好地平衡PP和PS成像反演的结果，我们在迭代过程中分别控制修正PP和PS成像的步长，使迭代过程稳定收敛.模型测试结果表明，与传统弹性高斯束偏移方法相比，最小二乘弹性高斯束偏移方法可以显著地提高成像结果的分辨率，提高成像剖面的保幅能力，以及增强复杂构造的成像照明度.