石墨-石英模型电导率的数值模拟研究及地球物理应用
郭颖星, 朱涛, 郑军
1 中国地震局地球物理研究所, 北京 100081 2 中国地质科学院, 北京 100037
0 引言
地球物理探测结果揭示大陆中下地壳及上地幔顶部普遍存在着高导异常及各向异性特征(Shankland and Ander, 1983; Ogawa et al., 2001; Heinson et al., 2005; Worzewski et al., 2011; Ichihara et al., 2014, Ye et al., 2019),其电导率可高达10-1S·m-1(Shimojuku et al., 2014)且无法用单一的机制解释(Jones, 1992).高导异常常见的成因理论——互联的颗粒边界熔体或流体(Gaillard et al., 2008; Yoshino, 2010; Baba et al., 2010),矿物所含的水(Karato, 1990; Poe et al., 2010; Gardés et al., 2014)和颗粒边界包裹的石墨薄膜或其他高导电矿物(Watson et al., 2010; Wang et al., 2013),在解释地壳普遍存在的各向异性及高导时均有一定的区域限制.下地壳在化学和物理性质上具有区域差异性(Rudnick and Fountain, 1995),影响其电导率的因素也很复杂.实验研究显示,对于镁铁质麻粒岩占主导的下地壳,水的存在能显著改变其所含矿物的导电特性,例如,含水斜长石具有电导率各向异性(Yang, 2012),而含有少量水的单斜辉石和斜方辉石电导率能达到地壳高导范围(Yang et al., 2011, 2012),含辉石层和含斜长石层互相交叠时便可造成显著的各向异性(Yang, 2011).同时,也有研究认为下地壳的导电因子可能是一些微小的晶界成分,如孔隙流体和石墨薄膜(Hyndman et al., 1993),MT探测研究中常将断裂带附近的高导现象解释为含盐流体的存在(Hyndman and Shearer,1989; Shimojuku et al., 2014; Guo et al., 2015; Sakuma and Ichiki, 2016),而在火山地区,高导则常被归因为熔体的贡献(Ichiki et al., 2000; Li et al., 2020).相对于其他高导理论模型,石墨膜模型是一种具有较强区域限制性的高导机制,这一理论的提出可以追溯到约40年前(如, Alabi et al., 1975; Duba and Shankland, 1982),由于石墨在深部地壳(和上地幔)中的稳定性受热力学因素控制,在呈氧化状态的深部地壳(和上地幔),石墨很难大量存在(Wood et al., 1990),但在一些呈还原环境的区域,可出现石墨的局部富集(Puelles et al., 2014; Jödicke et al., 2004, 2007; Rawat and Sharma, 2011; Zhu et al., 2020),在高级变质岩中甚至可以作为副矿物或成岩矿物出现(Luque et al., 2014;Touret et al., 2019).
自然界中的石墨主要由含碳流体沉积产生或者由变质过程中有机质转化而来(Jödicke et al., 2007; Huizenga and Touret, 2012),由流体沉积而成的石墨常呈现多种形态,而变质石墨则主要为片状晶体(Luque et al., 2012, 2014; Ai et al., 2020).研究显示很多断层的局部滑动带或者主滑动面上石墨(和碳)的含量高于5 vol.%(Oohashi et al., 2012; Kuo et al., 2014; 韩明明等, 2019),如龙门山断裂带(Wang et al., 2014; 陈进宇等,2017),日本Tanakura断裂带(Oohashi et al., 2011)等.对于断层带地区的高导异常,虽然流体成因是地学观测领域广泛接受的一种观点,但当断裂带中出现石墨局部富集时,在剪切应力作用下,石墨可能发生形态、分布以及排列方式的变化而实现相互连接(Puelles et al., 2014),从而影响断裂带的导电特征(Frost et al., 1989; Glover anddám, 2008,陈进宇等,2017;Ye et al., 2019,韩明明等,2019).
研究发现,矿物颗粒表面覆盖少量石墨便可达到地壳或上地幔的电导率范围(Duba and Shankland, 1982; Mareschal et al., 1992).由于石墨薄膜很薄,以至于用普通光学和扫描电镜观察不到而被长期忽略(Frost et al., 1989, 朱茂旭和谢鸿森,1999),且在抬升至地表后,石墨薄膜连通性也会发生不可逆的破坏(Frost et al., 1989; ELEKTB Group, 1997),从而增加石墨薄膜高导的实验观测难度.石墨对地壳岩石导电性的影响,前人做了一些相关工作.Jödicke等(2007)研究了意大利Serre San Bruno石墨石英岩的电学性质,认为经变质和剪切作用形成的瓦片状孤立石墨颗粒阻止了电路的互连,致使高达12%~15%石墨浓度的石英岩呈现高阻性.当孤立的石墨颗粒在隆升过程中被机械地涂到连续路径上,通过剪切产生所观察到的石墨网络,造成高导电性(Jödicke et al., 2004),晶界周围50~200 Å厚的碳薄膜便可以使电导率增加到10-2S·m-1之上(Frost et al.,1989),而沿剪切带较厚的石墨薄片可以在更大程度上增加电导率(Heinson et al., 2005).在静压力下,石墨-石英混合样品在碳体积率达到6.46~6.73 vol.%时,石墨粉末实现完全连通(陈进宇等,2017),而在动态摩擦过程中需要的石墨含量则约为5 wt.%(韩明明等,2019).
石墨的连通情况会对含石墨岩石导电性造成较大的影响,而石墨的连通性与其在岩石中的含量、形态、排列结构等因素密切相关,数值计算方法对于矿物精确定量化的控制及在模型构建方面具有显著的优越性,在多矿物聚合物模型构建方面,可以很容易的解决诸如矿物排列方式、几何形状、比例含量等方面的问题,还可以实现对多变量模型中次要因素的限定,具有良好的可控性、可重复性等优点,在探讨模型电导率规律方面具有明显的优势.由于石墨引起的地壳高导异常是一种局部起作用的机制,本研究主要针对断裂带等石墨容易富集的构造区域,利用有限元数值模拟方法,选取地壳常见的造岩矿物石英,构建石墨-石英三维数值网格模型,模拟断裂带中石墨可能的存在状态,计算矿物颗粒边界覆盖石墨膜后模型导电性的变化,探讨断裂带地区高导异常及其各向异性与石墨的关系.
1 研究方法及模型构建
本文基于电量守恒定律和欧姆定律(ADINA R & D, Inc., 2012;郭颖星等, 2018;Garba et al., 2019),采用稳态电传导方法模拟矿物的导电情况.根据欧姆定律(公式(1)),电流与电压梯度呈正比例关系:
(1)
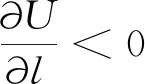
(2)
(3)
(4)
而模型内部电流平衡方程满足:
(5)
其中,jB为单位体积内电流的产生率.在模型体表面及外法线上所满足的边界条件为
U|S1=Ue,
(6)
(7)
其中,Ue为外表面电势,σn为面外法线方向n上的电导率,js表示电流通过S2面进入模型内部.
石英和石墨混合矿物模型设置成边长为10 cm的正方体(图1).模型上、下边界为等压面且电势分别为1.0 V和0 V,其他(侧)边界为绝缘面.采用四面体网格剖分方法,网格数约200万,节点数约35万(网格数选取方法详见第3节).通过对不同矿物的网格节点进行材料编号的方式区分模型中的石墨和石英.显微照片显示,片状石墨直径约为几十微米,而厚度约为几微米(Puelles et al., 2014),为方便计算,本研究将薄片状石墨直径与厚度比θ设置为10.令石墨薄片随机生成,并按不同角度定向排列且均匀分布,以模拟石英及其颗粒边界覆盖的石墨在剪切变形后石墨的形态特征.模型中的孔隙也采用随机方法生成,通过设置孔隙度及孔隙大小,探讨孔隙存在情况下,地壳含石墨矿物电导率的变化.模型的初始材料参数为地壳温、压条件下实验室内测量的石英和石墨的电导率(选取方法详见第2节).

图1 石墨(红色)和石英(白色)混合物模型示意图(a) 随机朝向的薄片状石墨均匀分布在石英中; (b)—(j) 薄片状石墨与电流传导方向二面角分别为80°~90°、70°~80°、60°~70°、50°~60°、40°~50°、30°~40°、20°~30°、10°~20°、0°~10° (注:每个角度范围包括范围内最小值但不包括最大值,之后的表述含义相同); (k)—(o)随机朝向的薄片状石墨均匀分布下,孔隙度(蓝色)分别为1%、3%、5%、10%、15%的模型.Fig.1 Perspective view of three-dimensional finite element mesh models of graphite (red)-quartz (white) mixture(a) Randomly oriented flake graphite is evenly distributed in the quartz; (b)—(j) The dihedral angles of flake graphite and the current conduction direction are 80°~90°, 70°~80°, 60°~70°, 50°~60°, 40°~50°, 30°~40°, 20°~30°, 10°~20°, 0°~10°(Note: Each angle range includes the minimum value but not the maximum value, and the following expressions have the same meaning), respectively; (k)—(o) the porosities (blue) are 1%, 3%, 5%, 10%, 15% of randomly oriented distribution flake graphite models.
2 材料参数的选取
数值模拟过程中初始材料参数为实验室测量的石英和石墨的电导率(图2).石墨属于高导矿物,其电导率受温度影响不明显(图2;Duba and Shankland, 1982; Yoshino and Noritake, 2011),因此我们采用了实验室测量结果的平均值作为石墨的初始电导率.石英的电导率具有显著的各向异性,不同条件下的测量结果差异明显(图2;Jain and Nowick, 1982; Lazzari et al., 1988; Bagdassov and Delépine, 2004).由于本研究中不考虑石英的各向异性,因此选取的石英电导率初始材料参数为介于石英不同晶轴电导率之间的多晶石英样品测量结果(Bagdassov and Delépine, 2004).
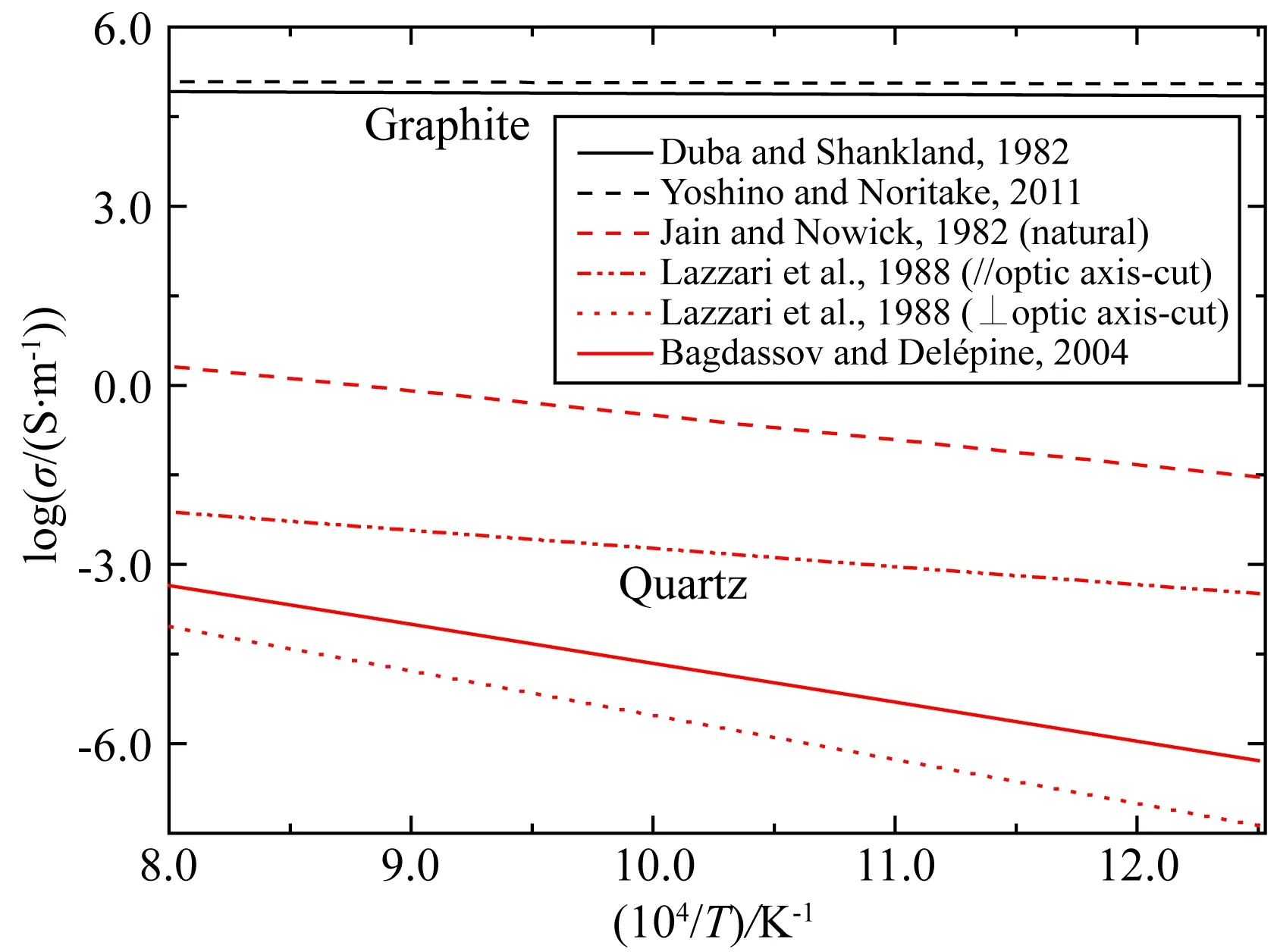
图2 石墨(黑色线)和石英(红色线)电导率的实验测量结果Fig.2 Experimental conductivities of graphite (black lines) and quartz (red lines)
石墨和石英的初始电导率参数如表1所示,对于模型中的孔隙,其电导率被设置为0.

表1 模型的初始电导率参数Table 1 Initial material parameters of electrical conductivities used in the numerical simulation
3 模型网格数选取
模型网格剖分情况关系着数值计算结果的精确性.一般情况下,网格数越多,计算结果越精确,但较大的网格数则会增加计算资源和时间,使计算效率降低(Abyn et al., 2014; Duan et al., 2015).为了选择出合适的网格数目,我们测试了0.5万、5万、10万、50万、75万、100万、150万和200万网格数目的计算精度.结果表明,当网格数大于10万时,模型计算结果的标准差随网格数的增加变化不大,200万网格与150万网格模型的标准差计算结果相差仅为1.08×10-6(图3),因此,综合考虑计算效率及计算精度的情况下,我们选取了200万作为本文矿物模型的剖分网格数.
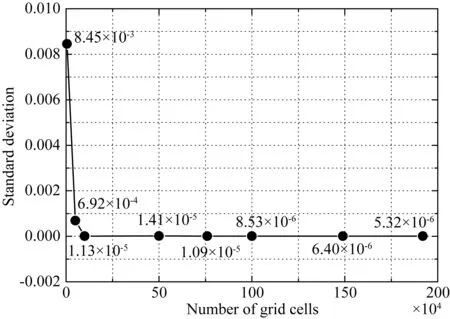
图3 网格数对计算结果标准差的影响(石墨含量为1 vol.%)Fig.3 The standard deviation of the calculated value of electrical conductivity varies with the cells number of the assemblage model (The contents of graphite in the models are 1 vol.%)
4 计算结果及分析
4.1 温度及石墨含量对模型电导率的影响
我们计算了不同温度下,薄片状石墨-石英随机方向分布模型的电导率随石墨体积含量的变化关系(图4).结果表明,在温度相同的情况下,随着石墨体积含量的增加,模型电导率也随之增大.当石墨体积含量达到连通阈值(约为6.5 vol.%)时,电导率急剧增大约3~4个量级(图4b).常温静压下的实验测量结果(陈进宇等,2017;陈进宇,2018)表明粉末状石墨-石英模型样品中碳体积率达到5.95~6.13 vol.%以及6.46~6.73 vol.%时,石墨形成部分连通和完全连通(图4b).我们数值计算获得的阈值(约为6.5 vol.%)位于实验获得的静压力下石墨完全连通(6.46~6.73 vol.%)的范围.当石墨含量低于该阈值(6.5 vol.%)时,随着石墨含量的增加,不同温度下的电导率的幅度增大了约2~4.5个量级,且温度越低,电导率幅度增加的量级越大(图4b),即温度也对模型的电导率存在显著的影响.不过,温度的影响会随着石墨含量的增加而逐渐减弱.当温度从560 ℃(104/T=12 K-1,)增大到977 ℃(104/T=8 K-1),在石墨含量接近0 vol.%时,模型电导率增加了约3个数量级,但增加的幅度值不超过0.1 S·m-1.随着石墨含量逐渐增加到石墨连通的阈值(6.5 vol.%),最高(104/T=8 K-1)和最低温度((104/T=12 K-1))的模型电导率之间的差异则小于1个量级.当石墨含量高于此阈值(6.5 vol.%),随着温度的增大,模型电导率的幅度值增加显著.例如,当石墨含量为14.3 vol.%,最高温度模型电导率相对于最低温度的增加量大于500 S·m-1(图4a),但在量级上则变化不明显(图4b),这一现象反映了石墨-石英模型随石墨含量的增加,主要导电矿物从石英转变为石墨的过程,即当石墨含量较低(低于连通阈值)时,模型的电导率主要由石英控制,呈现出对温度显著依赖的特征,而当石墨含量较高(高于连通阈值)时,模型的电导率主要由石墨控制,对温度依赖较弱.
4.2 石墨排列方式对模型导电性的影响
4.2.1 石墨排列方式对模型电势、电流分布的影响
设置石墨-石英混合模型中薄片状石墨与模型电流传导方向呈90°(与上下表面平行)(图5a)、0°(与上下表面垂直)(图5c)以及随机方向均匀分布于数值模型中(图5b),模型中石墨含量设置为约1 vol.%(各子图①、②)及10 vol.%(各子图③、④),分别计算施加电压后矿物模型中电势及电流的分布情况(图5).当模型中片状石墨含量为1 vol.%时,3个石墨排列方式模型的电势和电流均难以在模型中传导,模型中的石墨处于孤立状态,石墨上的电势与电流与石英上的接近.而当石墨含量增加到10 vol.%时,3个模型上部石墨分布区域的电势明显高于石英区域,且沿电流传导方向电势逐渐降低;在模型底部,石墨和石英分布区域的电势相近且接近于0(图5).相对于薄片状石墨垂直于电流传导方向的情况,随机方向分布和平行于电流传导方向分布的石墨更容易在电流传导方向上实现网络状连通,从而将高电势传导到模型下部(对比图5a和图5b或图5c).电流分布情况与电势分布情况类似,当薄片状石墨垂直于电流传导方向时,石墨在模型中呈现层状分布,难以在电流传导方向上形成连通良好的网路,而当薄片状石墨随机方向分布或平行于电流传导方向时,石墨沿电流方向容易实现连通,从而使电荷沿石墨分布路径实现迁移.
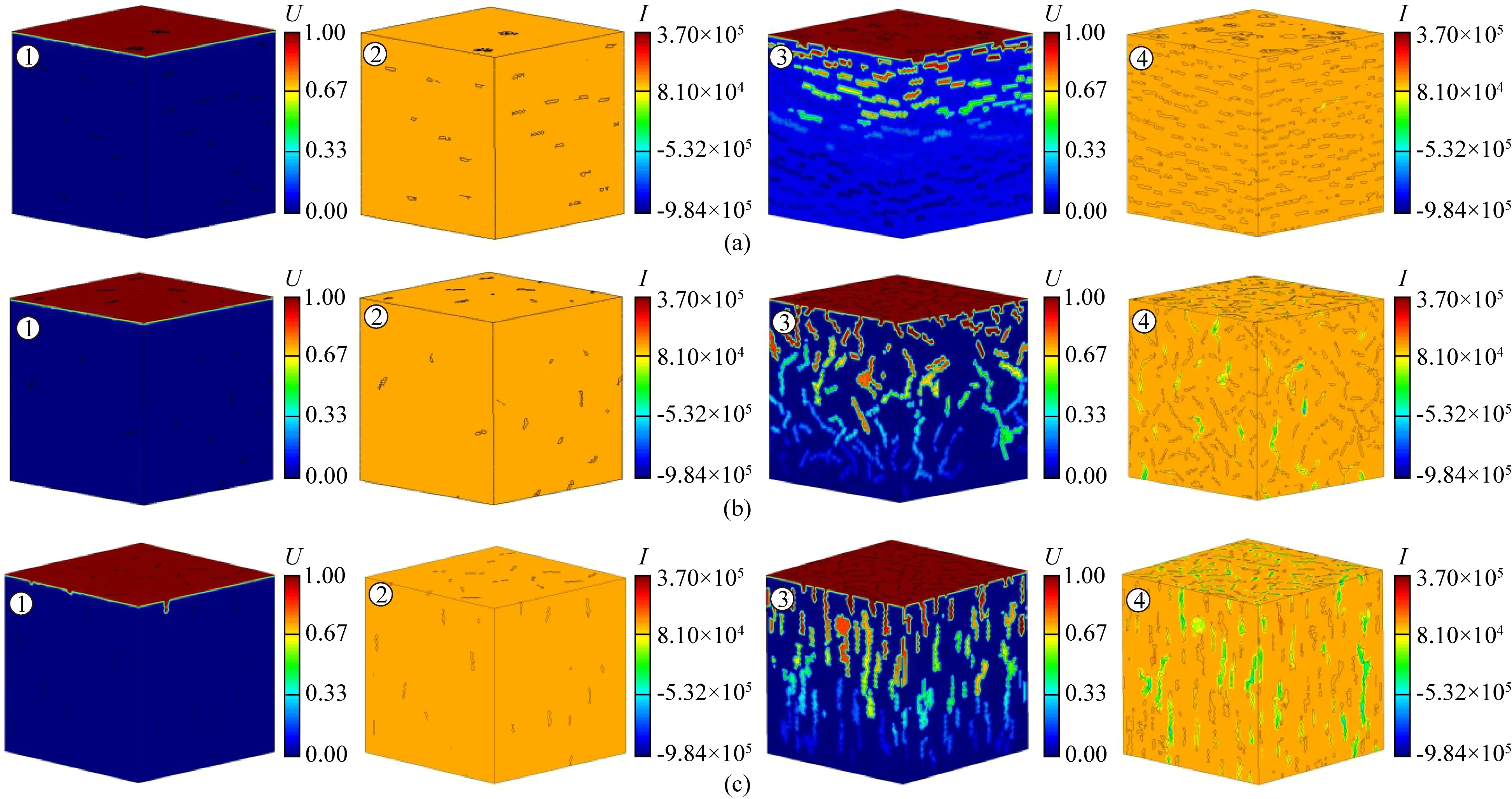
图5 石墨-石英模型电势、电流随石墨体积含量及排列方向的变化数值模型的计算温度为727 ℃(104/T=10 K-1)(a)片状石墨与电流传导方向垂直(平行于矿物模型上下表面);(b)片状石墨随机方向分布于矿物模型中;(c)片状石墨与电流传导方向平行(垂直于矿物模型上下表面),各子图①、②石墨含量约为1 vol.%,③、④含量约为10 vol.%.Fig.5 The electric potential and current change with graphite volume content and arrangement directionThe calculated temperature of the numerical model is 727 ℃ (104/T=10 K-1) (a) The flake graphite is perpendicular to the current conduction direction (parallel to the upper and lower surfaces of the mineral model); (b) The flake graphite is distributed in random directions in the mineral model; (c) The flake graphite is parallel to the current conduction direction (perpendicular to the upper and lower surfaces of the mineral model), the graphite content in each sub-picture ① and ② are about 1 vol.%, and the content of ③ and ④ are about 10 vol.%.
4.2.2 石墨排列方式对模型电导率的影响
石墨的定向排列能使形成良好石墨连通网路所需要的石墨含量降低(韩明明等,2019),为探讨模型电导率与石墨排列方向之间的关系,我们设置薄片状石墨与电流传导方向(垂直于模型上下表面)的夹角φ分别为80°~90°、70°~80°、60°~70°、50°~60°、40°~50°、30°~40°、20°~30°、10°~20°及0°~10°,且在模型中均匀分布.获得了这些模型在温度为727 ℃时的电导率随石墨含量的变化特征(图6).对于薄片状石墨的所有排列方向的模型,电导率均随石墨含量的增加而增大.当石墨含量相同时,φ角度越小,模型的电导率越大,而φ由40°~50°增大到50°~60°时,电导率幅度变化最大,而接近0或90°时,φ角度变化对电导率影响较小.在石墨含量达到连通阈值前后,模型电导率发生了4~5个量级的阶跃性增大.当石墨含量低于该阈值时,相同石墨含量的模型电导率受φ角度变化的影响较小,φ从80°~90°减小到0°~10°时,电导率最大增量约为0.5个数量级.当石墨含量高于该阈值时,相同石墨含量下,φ从80°~90°减小到0°~10°时,电导率最大增量则接近2个数量级.φ对模型的阈值范围也有影响.当φ为80°~90°时,模型电导率发生显著增大的石墨含量阈值约为7.1~8.2 vol.%,而当φ减小到0°~10°时,石墨含量阈值约为5.3~5.7 vol.%,即阈值随φ角度的减小而降低.石墨随机方向分布模型的电导率(图6中的黑色圆点)及电导率显著增大的阈值(约6.5 vol.%)与φ为30°~40°的模型结果最为接近.由此可以得出,薄片状石墨的定向排列能较显著地改变石墨-石英模型的导电性,其中石墨平面沿电流传导方向排列时,形成电流通路需要的石墨含量最低.
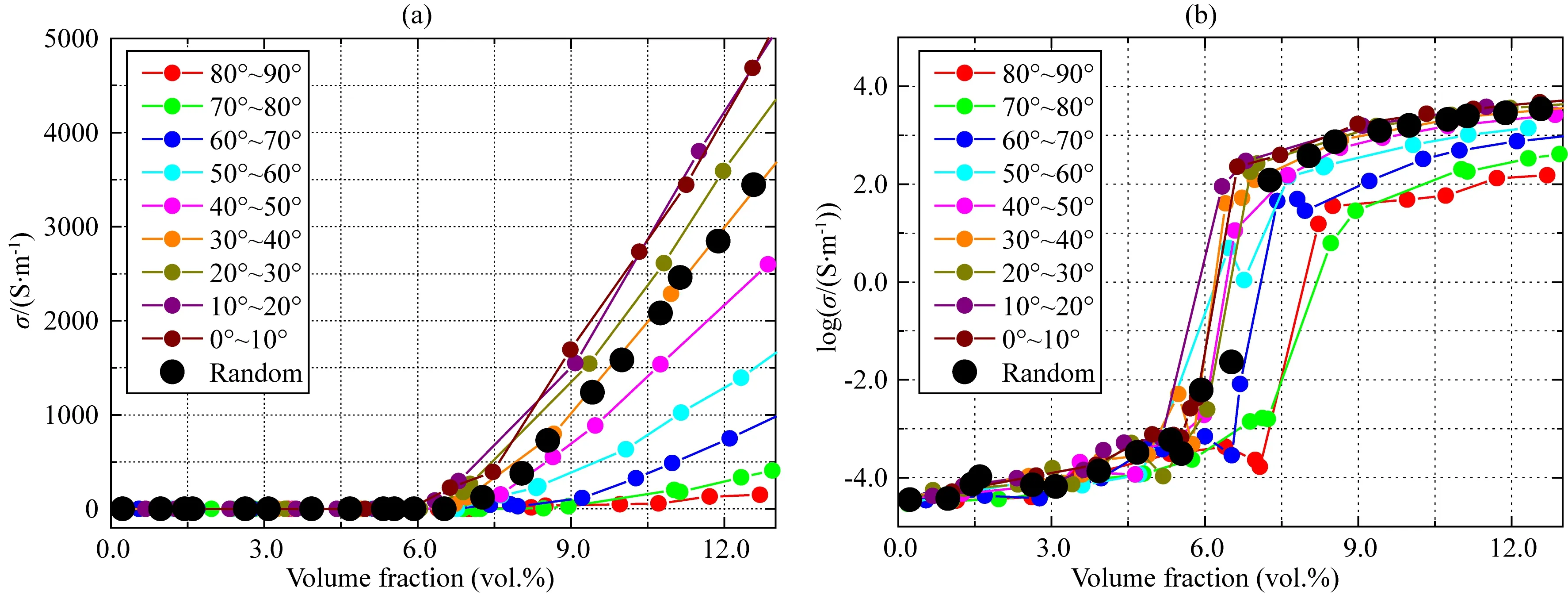
图6 石墨排列方向对模型电导率的影响温度为727 ℃(104/T=10 K-1),(a)为自然坐标,(b)为对数坐标.彩色图标代表片状石墨与模型电流传导方向(垂直于模型上、下表面)的夹角分别为80°~90°、70°~80°、60°~70°、50°~60°、40°~50°、30°~40°、20°~30°、10°~20°、0°~10°,黑色实心圆为石墨随机方向分布的模型.Fig.6 The effect of graphite arrangement on the electrical conductivities of the modelThe temperature is 727 ℃ (104/T=10 K-1), (a) is the natural coordinate, and (b) is the logarithmic coordinate. The color icons represent the angles between the flake graphite and the current conduction direction (perpendicular to the upper and lower surfaces of the model) are 80°~90°, 70°~80°, 60°~70°, 50°~60°, 40°~50°, 30°~40°, 20°~30°, 10°~20°, 0°~10°, the black solid circle are the electrical conductivities of the model with graphite distributed in random directions.
4.3 孔隙度对石墨-石英模型电导率的影响
石英颗粒边界存在孔隙,在地壳压力的作用下,孔隙大小会发生改变,会对模型的电导率造成一定的影响(Glover and Vine, 1995; ELEKTB Group, 1997),我们设定模型中片状石墨与石英的体积比分别为1∶9及1∶19(即:石墨/(石英+石墨)的体积百分比(设为α)分别为10 vol.%和5 vol.%),在模型中设置不同的孔隙度,并改变孔隙的体积,以探讨孔隙度及孔隙大小对模型电导率的影响(图7).结果表明,当模型中α为5 vol.%时,在孔隙度从0增大到70%的过程中,计算的模型电导率在量值上没有发生明显的变化,而当α为10 vol.%时,电导率则随孔隙度的增大而减小,并在孔隙度约为35~40%附近,模型电导率发生明显的阶跃式降低.这主要是由于α为5 vol.%时,石墨体积不超过模型总体积的5 vol.%(孔隙度为0时石墨体积含量为5 vol.%),小于模型电导率显著增大时的石墨含量阈值(约6.5 vol.%),石墨无法实现连通,从而使模型处于低导状态,此时模型的电导率主要受石英控制.而当α增大到10 vol.%时,虽然孔隙的存在会减弱石墨的连通性,但由于石墨的含量最高可达10 vol.%(孔隙度为0时),在孔隙度的增加过程中,会出现等效于石墨含量接近阈值的情况,从而导致模型电导率发生显著的阶跃变化.
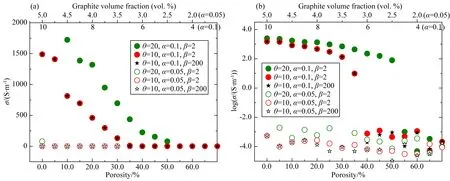
图7 孔隙度对石墨-石英模型电导率的影响计算温度为727 ℃(104/T=10 K-1).(a)为自然坐标,(b)为对数坐标.θ为薄片状石墨直径与厚度的比值,α为石墨与(石墨+石英)的体积比,β为组成每个孔隙的网格数.Fig.7 The influence of porosity on the electrical conductivities of the graphite-quartz modelThe calculated temperature is 727 ℃ (104/T=10 K-1). (a) is the natural coordinate, (b) is the logarithmic coordinate. θ is the ratio of the diameter to the thickness of the flake graphite, α is the volume ratio of graphite to (graphite+quartz), and β is the number of grids that make up each pore.
为进一步探讨孔隙体积对模型电导率的影响,我们针对网格模型的特点,设定了一系列孔隙体积的模型,组成每个孔隙的网格数β最小为2,最大为200.并选取β为200和2个网格的情况来进行说明.结果表明,当α为10 vol.%时,两种孔隙尺寸下模型的电导率除个别数据点外变化不明显,因此我们认为在模型中石墨形态及排列方式不变的情况下,仅仅改变孔隙的尺寸对模型的电导率影响并不明显.我们进一步设定θ值从10增大到20且每个孔隙由2个网格组成,相同孔隙度下的α为10%的模型电导率最大增量可达6个数量级,且θ为20的模型在孔隙度从0%增大到70%的过程中,其电导率在孔隙度约为50%~55%时发生明显的阶跃式降低,表明θ的变化不仅能改变模型电导率,而且可以改变电导率发生显著变化时的石墨含量阈值.结合数值计算结果,我们认为石墨在石英中沉积、渗透过程中会受到石英形态的影响,孔隙尺寸的改变往往伴随着石墨形态的改变及θ值的变化,石墨体积含量不变的情况下,如果石英矿物之间孔隙尺寸增大造成石墨θ值增大,则会使模型中的石墨连通变得更加容易.
5 地球物理应用
在岩石圈6~50 km的深度范围内,高导异常值约为0.028~0.67 S·m-1(Shankland and Ander, 1983;Shimojuku et al., 2012).中国大陆壳内高导层隆起的区域多位于活动构造区,对应韧性剪切带(张继红等,2010).虽然剪切断裂带岩石破坏区充填液体后可以造成高导(尹曜田,2014),然而考虑到断裂带中石墨存在的可能性,相互连通的石墨也可为断裂带的高导现象提供一种可能的解释.
石英和长石作为地壳最主要的造岩矿物,实验室内测得的电导率(Lazzari et al., 1988; Bagdassarov and Delépine, 2004; Wang et al., 2010; Hu et al., 2013, 2015)远低于高导异常区域的电导率值(图8),这两种矿物的电导率实验测量结果均无法解释地壳的高导现象.由于石墨主要由变质过程中有机质转化或者由含碳流体沉积产生,对于一些处于还原环境的断裂带区域,石墨有可能形成局部富集而达到较大的丰度.同时,在地壳构造运动挤压及剪切应力的长期作用下,含石墨岩石因剪切变形、孔隙压实等变化造成石墨部分连通及定向排列,这些因素可能使得地壳石墨富集区域呈现出高导异常及各向异性特征.
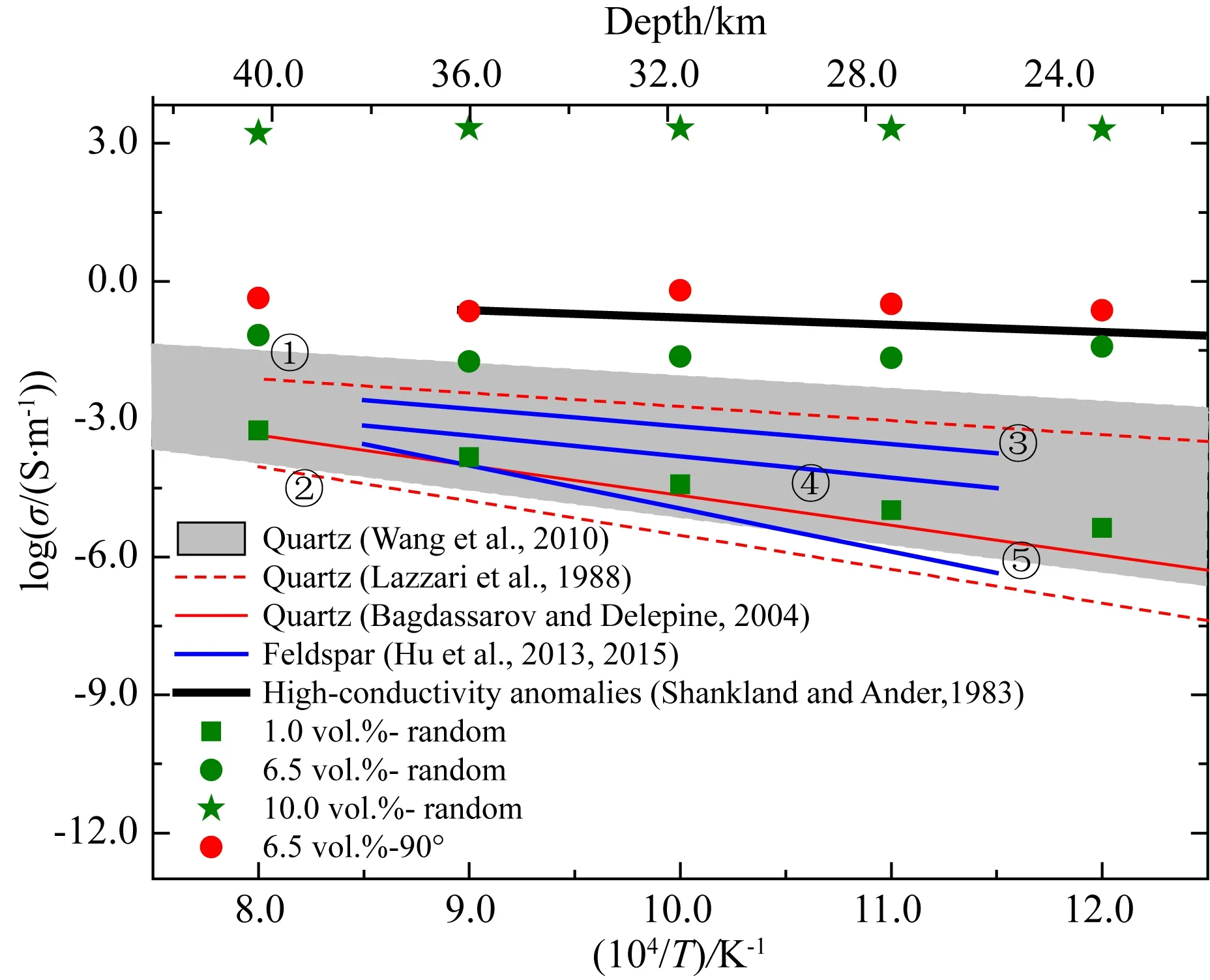
图8 长石、石英电导率及石墨-石英数值模型电导率结果与地壳高导异常的对比地温梯度采用25 ℃/km.粗实线为地壳高导异常电导率结果,灰色阴影及红色虚线为石英不同方向的电导率结果,其中①和②分别为平行和垂直于c轴的情况,红色实线为多晶石英样品测量结果.蓝色实线为长石的电导率实验测量结果,其中③、④、⑤分别为钠长石、钾长石和钙长石.绿色图标为片状石墨随机方向分布的电导率结果,方形、圆形和星形为片状石墨含量分别为1 vol.%、6.5 vol.%、10 vol.%的情况,红色圆形图标为片状石墨与上、下表面呈90°(沿电流传导方向),含量为6.5 vol.%的情况.Fig.8 A comparison of electrical conductivities of feldspar, quartz, and graphite-quartz numerical model with high conductivity anomalies of the crustThe ground temperature gradient is 25 ℃/km. The thick solid line is the result of the high-conductivity abnormal of the crustal, the gray shadow and red dashed line are the result of the electrical conductivity of the quartz on different directions, ① and ② are parallel and perpendicular to the c axis, respectively. The red solid line is the result of the polycrystalline quartz sample. The blue solid lines are the experimental result of the electrical conductivities of feldspar, ③, ④, and ⑤ are albite, K-feldspar, and anorthite, respectively. The green icons are the electrical conductivities of flake graphite distributed in random directions. The square, circle and star are the flake graphite content of 1 vol.%, 6.5 vol.%, and 10 vol.% respectively. The red solid circles are the flake graphite is 90° to the upper and lower surfaces (in the direction of current conduction) with the content of 6.5 vol.%.
我们的计算结果表明(图8),当石墨-石英模型中薄片状石墨随机分布且含量为1 vol.%时,模型电导率比地壳及上地幔顶部高导异常区的(0.028~0.67 S·m-1;Shankland and Ander, 1983;Shimojuku et al., 2012)低约3~4.5个数量级;当石墨含量为6.5 vol.%,薄片状石墨随机方向排列时,模型电导率略低于高导异常区的电导率值,薄片状石墨沿电流传导方向定向排列时,模型电导率略高于高导异常值;当石墨含量为10 vol.%时,模型电导率则比高导异常区的高约4~4.5个数量级.这些结果表明,当地壳石英中石墨含量高于6.5 vol.%时,石墨-石英模型可以作为地壳或上地幔顶部高导异常区的一种形成机制.
6 讨论及结论
通过构建石墨-石英有限元数值模型,探讨了温度、石墨定向排列及模型孔隙度对电导率的影响.得出以下结论:
当薄片状石墨随机方向均匀地分布在模型中时,相同温度下,模型的电导率随石墨含量的增加而增大.当石墨含量达到石墨连通的阈值(θ=10时,约6.5 vol.%)时,模型电导率会发生显著的增大;当石墨含量低于阈值时,模型电导率与石英的接近,且对温度具有较强的依赖性.400 ℃的温差可造成高达3个数量级的电导率差异,但随着石墨含量的增加模型电导率对温度的依赖性逐渐减小.当石墨含量高于阈值时,模型处于高导状态,电导率随温度的增加变化不明显.400 ℃的温差几乎不会引起模型电导率在量级上的改变,与石墨的导电特征一致.当石墨含量在阈值附近时,模型电导率呈现出相对低导且对温度影响不敏感的特征.模型电导率随石墨含量增加的导电特征符合逾渗理论(Gueguen and Dienes, 1989; Wang et al., 2013; 陈进宇等,2017).
石墨排列方向的改变会导致石墨-石英模型电导率的显著变化以及模型电导率显著增大时的石墨含量阈值的改变.当石墨与电流传导方向的夹角φ从80°~90°减小到0°~10°时,模型电导率的最大增量可以达到~2个数量级,电导率发生显著增加的石墨含量阈值由约7.1~8.2 vol.%减小为约5.3~5.7 vol.%.这些结果表明薄片状石墨的排列方式对石墨的连通性有显著的影响,平行比垂直于导电方向的石墨排列方式更有利于形成沿电流传导方向上的通路.
孔隙度对模型的电导率也有较显著的影响.一般情况下,模型电导率随孔隙度的减小而增大.在石墨固定的情况下,孔隙尺寸的改变对电导率的影响较小.θ值的增大会导致模型电导率的显著增加.
在地壳活动显著的剪切断裂带区域,虽然高导流体的存在被认为是断裂带导电性的主要影响因素,但考虑到石墨存在的可能性,相互连通的石墨可能与某些断裂带的高导现象有关,而石墨的定向排列也可为断裂带电导率各向异性提供一种解释.
致谢本文在模型构建过程中得到李平恩副研究员的指导和帮助,审稿专家提出的宝贵建议对文章的改进有很大的帮助,特此致以衷心的感谢.

