平流层爆发性增温期间赤道电集流中太阴潮汐的经度变化统计学研究
郑志超, 王慧, 张科灯, 何杨帆, 高洁, 孙璐媛, 仲云芳
武汉大学电信学院空间物理系, 武汉 430072
0 引言
平流层爆发性增温(Sudden Stratospheric Warming,SSW)是发生在冬季平流层的大尺度气候现象,其主要特点是冬季极区平流层温度突然升高和平均纬向风减弱甚至转向(e.g., Andrews et al., 1987).自20世纪50年代以来,人们对该现象进行了广泛的研究,它由快速增强的准静态行星波与平均纬向环流的相互作用引起(Matsuno, 1971).虽然SSW发生在平流层高度,但相关研究表明,它对中间层和较高高度的热层也存在显著的影响(Liu and Roble, 2002).对SSW现象的研究有助于加深人们对大气层-电离层-热层耦合过程的理解.
电离层对SSW的响应一直以来是研究的热点.在SSW期间,潮汐波与行星际波的非线性耦合作用会引起电离层参数出现明显的波动,如电子密度、垂直漂移速度和赤道电集流(Equatorial Electrojet, EEJ)(Fejer et al., 2010; Maute et al., 2015; Sridharan, 2017).其中,EEJ会出现明显的半日波动,研究表明这与太阴潮汐的增强有密切关系(Fejer et al., 2010).太阴潮汐源于地球和月亮之间的引力,幅度最大的部分来自于12.42太阴时(M2),其在新月和满月时会达到极值(Thurman, 1994).20世纪40年代,人们发现太阴半日潮汐对EEJ存在调制作用,其峰值出现在冬季(Bartels and Johnston, 1940).后来的研究证实了这一发现,并揭示出太阴潮汐的增强与北半球冬季平流层爆发性增温有关(Fejer et al., 2010; Stening, 2011; Park et al., 2012).SSW期间太阴潮汐的增强与背景条件的变化有关,背景风场的分布导致大气的Pekeris共振峰周期偏移到了12.42太阴时,这与太阴半日潮汐频率接近(Forbes and Zhang, 2012).在此基础上,人们进一步研究了SSW对EEJ中太阴半日潮汐M2分量的影响.Yamazaki(2013)利用Addis Ababa地磁台站数据进行统计学研究发现,有SSW发生的冬季EEJ的太阴潮汐M2分量的幅度大约是没有SSW发生冬季的3倍.利用时序叠加分析方法,Siddiqui等(2015)发现秘鲁扇区EEJ的太阴半日潮汐M2分量的峰值要提前于高纬度平流层温度的峰值.在一些SSW事件中,EEJ的太阴半日潮汐幅度可以与太阳半日潮汐相当 (Sathishkumar and Sridharan, 2013;Siddiqui et al., 2018).并且,EEJ中太阴半日潮汐M2分量的幅度存在太阳活动、极区涡流类型和准两年振荡(quasi-biennial oscillation,QBO)相位依赖性,EEJ的太阴潮汐M2分量在东相QBO(eQBO)时的强度要大于西相QBO的(wQBO)(Siddiqui et al., 2018).
EEJ的经度变化的研究十分重要,有大量的工作来说明和解释EEJ的经度结构(Lühr et al., 2008; Wang et al., 2020).EEJ中太阴潮汐本身也存在经度变化,而且经度结构与EEJ不同(Yizengaw and Carter, 2017; Yamazaki et al., 2017).所以研究EEJ中太阴潮汐的经度变化,对我们加深对EEJ的理解具有重要意义.虽然目前对SSW期间EEJ中太阴潮汐变化的研究很多,但对其经度变化的研究较少.Siddiqui 等(2017)基于地磁台站和卫星数据,分析了SSW期间EEJ中太阴潮汐的经度变化,结果显示秘鲁扇区太阴潮汐的强度要比印度扇区强,并认为经度变化产生的原因可能与风发电机区动力学过程有关.目前缺乏EEJ中太阴半日潮汐经度变化的统计学研究,为更全面地了解SSW中EEJ的太阴半日潮汐的变化特征,本文利用印度和秘鲁地区数十年的地磁数据,并结合CHAMP卫星和SWARM卫星的磁场数据,首次对SSW期间EEJ中太阴半日潮汐的经度变化进行了统计学分析,揭示了不同经度带SSW期间太阴潮汐的定量特征,并对有关经度差异进行了解释.
1 数据和方法
1.1 数据
本文使用的EEJ地基数据来自于地磁台站测量的水平磁场数据,计算EEJ的原理是用位于磁赤道地磁台站的水平磁场数据减去相同经度的非磁赤道低纬度地磁台站的水平磁场数据(Anderson, 2004).印度扇区EEJ可以根据Tirunelveli(简称TIR, 8.7°N, 77.8°E, 磁纬度0.59°N)、Trivandrum(简称TRD,8.48°N,76.9°E,磁纬度0.29°N)和Alibag(简称ABG, 18.6°N, 72.9°E, 磁纬度13.67°N)地磁台站的水平磁场数据计算得到.根据Huancayo(简称HUA,-12.05°N, 75.3°W, 磁纬度0.59 °N)和Fuquene(简称FUQ, 18.11°N, 66.2°W, 磁纬度17.06°N)地磁台站水平磁场数据可以计算出秘鲁扇区的EEJ.在本研究中,所用的地磁台站数据为1 h数据精度的水平磁场数据,具体计算方法可以参见Wang等(2020).
另外,在本文使用的低轨卫星观测的EEJ数据主要利用CHAMP和SWARM卫星的1 Hz的标量磁场数据反演得到.CHAMP卫星和SWARM卫星是极轨卫星,CHAMP/SWARM卫星的轨道倾角分别为87.3°/87.5°,飞行周期均为93 min.CHAMP卫星初始高度为450 km,覆盖所有地方时大概需要131天.SWARM-A和SWARM-C飞行高度约为470 km,覆盖所有地方时需要将近133 d.SWARM-B飞行高度约为520 km,覆盖所有地方时需要145 d(Reigber et al., 2002; Friis-Christensen et al., 2008).利用卫星标量磁场数据反演EEJ的方法可参考Lühr 等(2004).
在本研究中,SSW期间 30 km高度(10 hPa)上北纬60°平均纬向风和平均纬向温度的再分析数据可以从ERA-40(1958—2002)(Uppala et al., 2005)和ERA-interim(1979—2019) (Dee et al., 2011)获得,表1给出了SSW事件列表和磁场数据来源,表中的中心日期指的是SSW期间极区涡旋发生分裂或者偏移的时间.
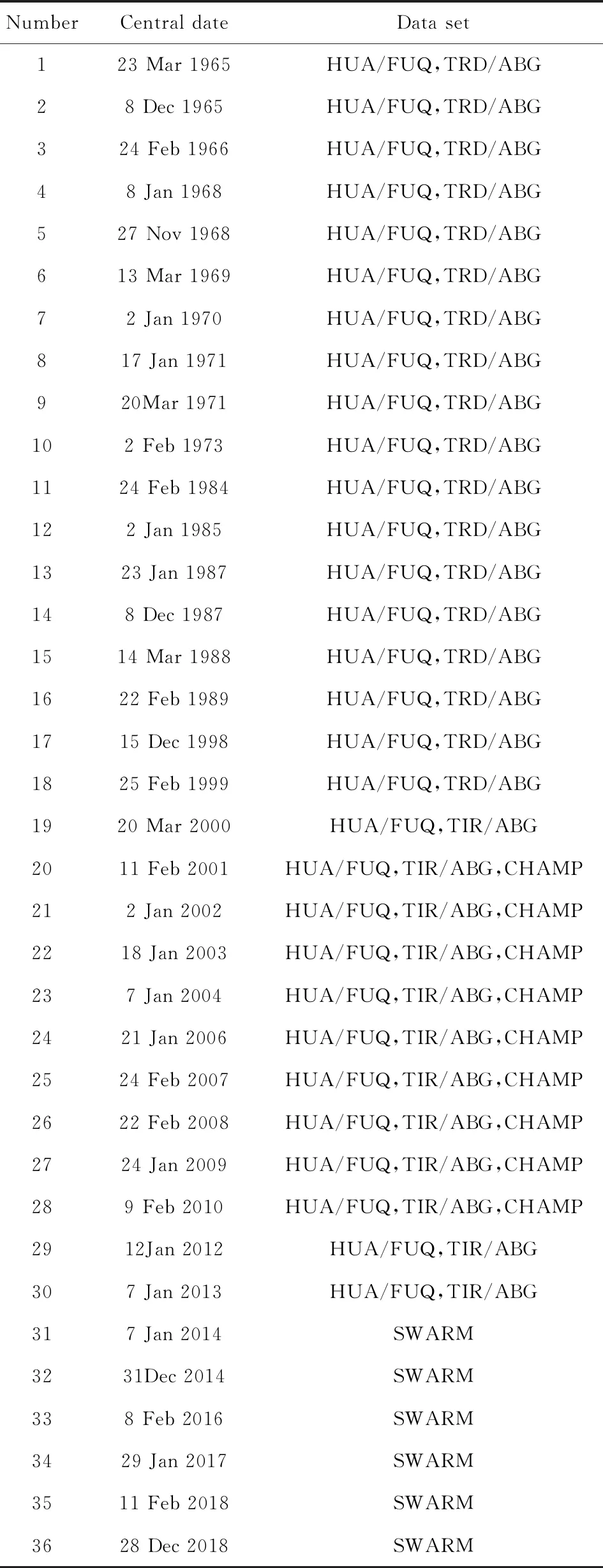
表1 SSW事件列表和磁场数据来源Table 1 The list of SSW event and data usage
1.2 从地磁台站EEJ中提取太阴潮汐的方法
太阳周日潮汐(24 h)、半日潮汐(12 h)、8 h和太阴半日潮汐(12.42 h)是EEJ中主要的潮汐分量,在提取各分量之前,应先剔除太阳活动的影响.EEJ与太阳活动可近似看成线性关系,在本研究中我们根据Alken和Masu(2007)提出的关系式对EEJ进行了归一化处理,归一化公式如下:
EEJn=4.458×10-5×(150-F10.7)+EEJobs,
(1)
公式(1)中EEJn为归一化之后的EEJ,F10.7为观测是太阳活动指数,EEJobs为EEJ观测值.得到归一化之后的EEJ后,我们采取了与Siddiqui 等(2015)相似的方法从地磁数据中提取潮汐分量的方法,提取公式如下:
(2)
sn和σn分别代表太阳潮汐对应n次谐波分量的幅度和相位,t表示太阳地方时,τ表示太阴地方时(新月对应0 h,满月对应12 h),L和λ分别代表太阴半日潮汐的幅度和相位.将观测数据代入公式(2)中,可得到EEJ强度与各潮汐分量的幅度与相位关系的方程组,再利用最小二乘拟合解方程组,就可以求解出各潮汐分量幅度和相位.
在实际的提取过程中,由于太阴半日潮汐和太阳半日潮汐的周期均在12 h附近,因此需要将他们分离开来.频率分辨率Δf可以用以下公式表示:
(3)

1.3 从卫星反演的EEJ中提取太阴潮汐的方法
卫星数据和地磁台站数据特点不同,每天可以得到16个EEJ数据,这些数据地方时基本相同,地理经度不同.正是由于其不同,卫星数据我们需要对进行地方时和太阳活动的归一化,且卫星数据只能提取太阴潮汐分量,而不能提取太阳潮汐分量,具体提取步骤如下.
EEJ对太阳活动、地方时和月相都存在依赖性,为了从卫星EEJ数据分离出太阴潮汐分量,应先将EEJ信号进行归一化处理,以去除太阳活动和地方时的影响.归一化公式如下(Park et al., 2012):
(4)
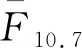
我们根据如下公式提取太阴潮汐:
(5)
公式(5)中L为太阴潮汐波,A为其幅度,d0太阴潮汐相位,d为太阴日,h为地方时,Tmoon太阴周期(29.53天).其中h和d存在如下关系:
(6)
公式(6)中,d1为任意相位,TCHAMP为261 d.整理公式(5)和公式(6),可以得到CHAMP卫星数据中,太阴半日潮汐的提取公式如下:
(7)
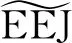
2 统计结果
图1a给出了1960—2013年冬季北半球平流层增温期间(总事件数30)太阳活动指数F10.7变化的统计结果,其中0时刻为表1中事件列表时间,实线两侧阴影部分为平均均方根误差.如图所示,在这30个事件中,太阳活动指数的均值在120左右,SSW发生前后变化不大.
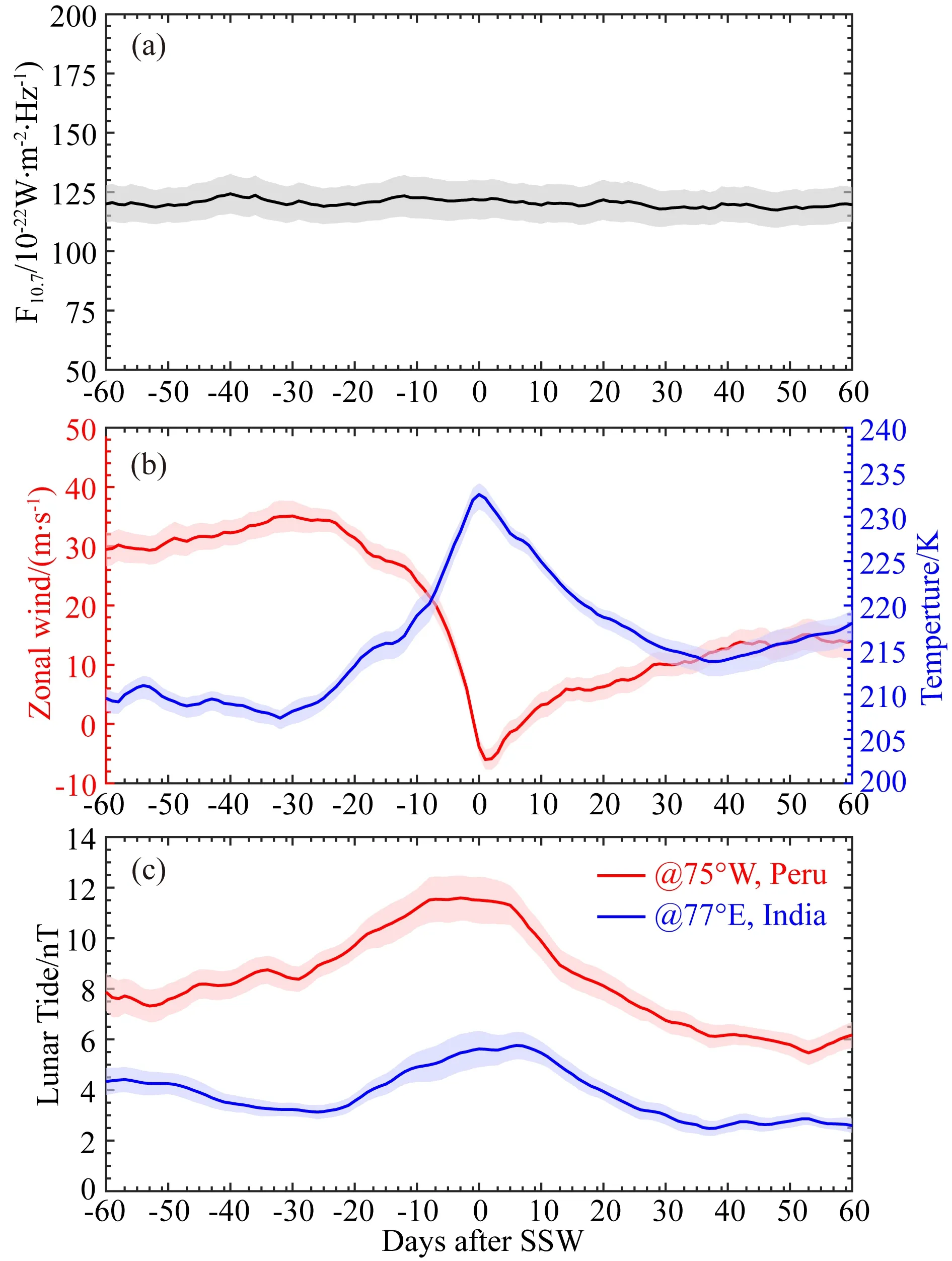
图1 SSW期间太阳活动指数F10.7(a)、60°N处10 hPa高度平均纬向温度(蓝色)和平均纬向风(红色)(b)、秘鲁扇区(红)和印度扇区(蓝)EEJ中太阴半日潮汐幅度(c)随时间变化图Fig.1 Daily variations of the solar activity index F10.7 (a), zonal mean temperature (red curve) and zonal mean wind (blue curve) at 60°N, 10 hPa (b) and lunar semidiurnal tidal amplitude in EEJ (c) based on Peruvian (red curve) and Indian (blue curve) station during SSW
图1b为SSW期间10 hPa高度上60°N处平均纬向风(东向为正)和平均纬向温度随时间的变化,其中红色表示平均纬向风,蓝色表示平均纬向温度.从图中可以看到,在-30天之前平均纬向风和平均纬向温度的变化比较稳定,纬向风接近30 m·s-1,温度约为210 K.从-30天开始,平均纬向温度逐渐升高,在0时达到峰值,峰值在230 K左右,之后逐渐下降,在35日左右趋于稳定,接近215 K.同时,东向平均纬向风从-30天开始减弱,在0时左右转为西向,3天后达到西向最强(-6 m·s-1),随后开始西向减弱,在40天左右达到稳定(15 m·s-1).
图1c为SSW期间EEJ 中M2分量的变化图,红色代表秘鲁扇区,蓝色代表印度扇区.在SSW期间,秘鲁扇区和印度扇区EEJ中M2分量均有明显增强.秘鲁扇区EEJ中M2分量在-60 d到-30 d期间在7~8 nT附近波动,之后开始上升,在第1 d达到峰值(11.6 nT),之后逐渐减弱,在40 d左右稳定.与印度扇区相比,在-60 d—到-25 d期间,EEJ中M2分量在3~4 nT附近波动,明显低于秘鲁扇区.然后在第5 d达到极值(约5.6 nT).随后开始减弱的过程,在35 d左右趋于稳定,幅度在2.7 nT左右.图中的虚线为大尺度变化趋势线,可以通过线性拟合得到.虚线和实线的对比可以看出,SSW期间太阴半日潮汐有明显的增强.
与图1类似, 本研究还统计了2001—2018年北半球SSW期间印度和秘鲁经度扇区卫星EEJ数据中M2分量的变化,共计15个事件,其结果如图2所示.图2a是SSW期间太阳活动指数F10.7的变化图,可以看出SSW期间太阳活动相对稳定,保持在110 s.f.u附近.

图2 格式与图1类似,但EEJ由CHAMP和SWARM卫星磁场数据得到Fig.2 The same as Fig.1, but the EEJ data from CHAMP and SWARM satellite
图2b显示在10 hPa高度上60°N的平均纬向风(东向为正)和平均纬向温度的变化,其中红色为平均纬向风,蓝色为平均纬向温度.平均纬向温度在-30 d之前,大约在205°附近,之后开始明显上升,在第2 d达到最高值231 K,之后开始降温,在35 d后趋于稳定.平均纬向风从第-25 d左右开始减弱,在第二天达到极小值,约为1.12 m·s-1,之后开始缓慢增强,30 d之后开始达到稳定状态.图2b中,平均纬向风和平均纬向温度与图1b中的变化情况基本一致,这反映了SSW期间平均纬向风和温度变化的典型特征,虽然存在细微的差别,这种差别可能是由于事件数的不同导致的.
图2c给出了CHAMP/SWARM卫星在SSW期间飞越印度扇区和秘鲁扇区是EEJ 中M2分量随时间的变化图,红色表示秘鲁扇区,蓝色表示印度扇区.通过与图1c的对比,可以看到卫星数据结果与地磁台站数据的一致性.秘鲁扇区EEJ 中M2分量的强度始终高于印度扇区,在SSW发生之前(-60 d到-30 d),秘鲁扇区EEJ 中M2分量的幅度高于印度扇区,分别为30 mA·m-1和19 mA·m-1左右.之后,随着平流层开始增温,EEJ 中M2分量开始增强,秘鲁扇区于第2 d达到最大(39.45 mA·m-1),印度扇区于第9 d达到最大(22.63 mA·m-1).达到峰值后,两经度带的EEJ 中M2分量开始减弱.
图2c和图1c的结果存在一定差别,主要表现为印度经度带太阴半日潮汐达到峰值的时间差不同.从地磁台站数据来看,印度台站EEJ 中M2分量达到峰值的时间为第5天.从卫星数据来看,印度扇区EEJ 中M2分量达到峰值的时间是第9 d.我们认为,这个差别可能来自于两方面,一方面是两个统计所用的事件数存在差别,另一方面是卫星数据用的是50°经度宽度的数据代表某一经度,不是严格的某个经度数据.用同样的方法,我们对2000—2010年相同的SSW事件做统计(本文没有给出相关图形),发现二者的差异较小.
潮汐除了幅度变化之外,相位变化也是很重要的信息.以往的研究表明EEJ中太阴半日潮汐波的相位变化受控于太阴时(月相),而每个SSW事件中心时间所对应的太阴时不同,因此很难直接统计单个台站的相位变化(Siddiqui et al.,2018; Sathishkumar and Sridharan, 2013).因此,在本研究将秘鲁扇区的EEJ中M2分量的相位减去印度扇区,统计结果如图3所示.从图3中可以看出SSW期间两地区相位差变化很小,在0.7 h以内,这表明SSW期间M2幅度的经度差异与相位差无关.Siddiqui等(2017)在分析SSW事件中M2的相位变化时也发现,秘鲁扇区和印度扇区相位变化差异较小.卫星数据的相位差结果与地面台站类似,本文没有给出.由于SSW期间,相位差变化较小,后面的讨论中将不再做详细讨论.
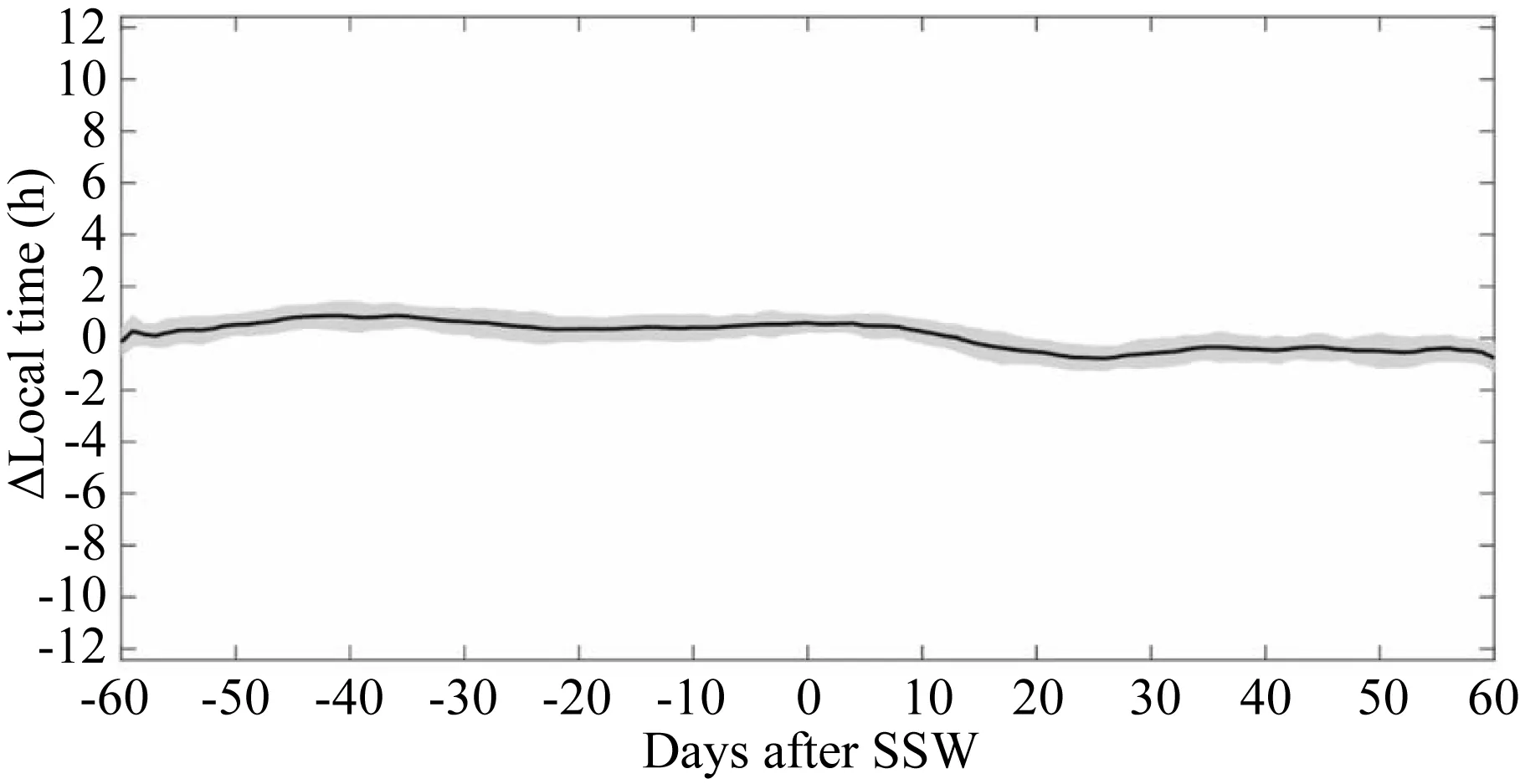
图3 SSW期间秘鲁和印度扇区地磁台站数据中EEJ的M2分量相位差的变化Fig.3 Daily variations of the lunar semidiurnal tidal phase difference in EEJ based on between Peruvian and Indian station during SSW
3 讨论
从图1和图2中可以看出SSW对印度和秘鲁扇区EEJ中的M2存在明显的调制作用,这两个扇区的EEJ中M2分量都得到了增强,并且存在明显的经度差异.首先,两个地区EEJ 中M2分量达到峰值时间不同.其次,两个地区EEJ 中M2分量的幅度不同.接下来,我们将对此进行讨论,并分析造成这些差异可能的原因.
3.1 峰值时间的经度差异
本文提取的太阴半日潮汐均为迁移潮汐,理论上应不存在经度差异.但背景大气条件(特别是纬向风)对太阴潮汐的传播有明显的影响(Stening et al.,1997).如图1c和图2c所示,印度扇区与秘鲁扇区相比,EEJ 中M2分量达到峰值的时间较晚,这一差异可能是由于两个地区的大气背景条件不同所致.直接探测印度扇区和秘鲁扇区背景大气条件的变化比较困难,以往的研究表明背景大气的改变与太阳活动和准两年振荡的相位有关(Labitzke,1987; Siddiqui et al., 2018),下面我们给出了在SSW期间EEJ的太阴半日潮汐在不同太阳活动水平和QBO相位时的变化情况.
本文对SSW期间印度和秘鲁扇区地磁台站的EEJ在不同太阳活动水平时的太阴半日潮汐的变化进行了统计,结果如图4所示,其中左图为太阳活动高年(F10.7>120 s.f.u),右图为太阳活动低年(F10.7≤120 s.f.u),相应的事件数分别为15和15.对比图4a和4b,我们可以看到太阳活动高年F10.7约为150 s.f.u,低年约为85 s.f.u,太阳活动高年和低年SSW期间平均纬向风和纬向温度的差异很小(图4c和4d).根据欧姆定律,EEJ的强度与电离层电导率成正比,而电离层电导率与F10.7指数有关(e.g.Robinson and Vondrak, 1984; Lühr et al.,2012).在图4e和4f中,虽然太阳活动高年EEJ的太阴半日潮汐幅度要强于低年,但是它的差别并没有像太阳活动指数差别那么明显,这也证实了Lühr等(2012)的理论,即EEJ 中M2分量的增强并不能完全用太阳活动指数来解释.虽然,太阳活动指数不足以解释其幅度变化,但我们可以看到,在太阳活动高年SSW期间,秘鲁扇区太阴半日潮汐达到峰值的时间是-5 d,印度扇区是5 d,秘鲁扇区要早于印度扇区.在太阳活动低年,印度扇区和秘鲁扇区的太阴半日潮汐在SSW期间增强过程明显,达到峰值的时间分别为第6和3 d.研究结果表明,印度扇区和秘鲁扇区的太阴半日潮汐在SSW期间达到峰值的时间与太阳活动有关,高太阳活动时秘鲁扇区太阴半日潮汐峰值时间要比低太阳活动时提前10 d左右,而对印度扇区的影响并不明显.综上所述,我们认为SSW期间EEJ 中M2分量达到峰值时间的经度差异与太阳活动水平有关.
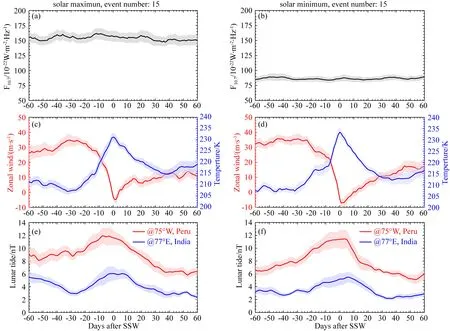
图4 太阳活动高年(左)和太阳活动低年(右)时SSW期间太阳活动指数F10.7(a,b)、60°N处10 hPa高度平均纬向温度(蓝色)和平均纬向风(红色)(c,d)、秘鲁扇区(红)和印度扇区(蓝)EEJ中太阴半日潮汐幅度(e,f)随时间变化Fig.4 Daily variations of the solar activity index F10.7 (a,b), zonal mean temperature (red curve) and zonal mean wind (blue curve) at 60°N, 10 hPa (c,d) and lunar semidiurnal tidal amplitude in EEJ (e,f) based on Peruvian (red curve) and Indian (blue curve) station during SSW at solar high activity (left) and solar low activity (right)
QBO相位影响潮汐传播不可忽视的影响因素,它不仅能影响底层大气,也能影响电离层(Yadav et al., 2019).在平流层东相QBO时,中间层的周日潮汐和半周日潮汐都会得到增强,在电离层则体现为电流和电场的增强(Davis et al., 2013; Chen et al., 2015).中间层的任何变化都可能会引起电离层电场或者电流的变化,QBO相位的改变可以引起背景风场的变化,从而影响太阴半日潮汐的向上传播过程(Siddiqui et al., 2018).为了进一步研究EEJ 中M2分量峰值时间与QBO相位的关系,我们根据Siddiqui等(2018)划分的SSW期间QBO相位类别,给出了在QBO东/西相位时,EEJ中太阴半日潮汐随时间的变化(图5).在图5e和5f中我们可以看到,东相QBO时(事件数19),印度和秘鲁扇区EEJ 中M2分量达到峰值的时间分别为第5和2 d附近,而西相QBO时(事件数11),印度扇区EEJ 中M2分量达到峰值的时间9天附近,而秘鲁扇区在-4 d.因此,我们可以认为SSW期间EEJ 中M2分量的峰值时间的经度差异可能与QBO相位有关.
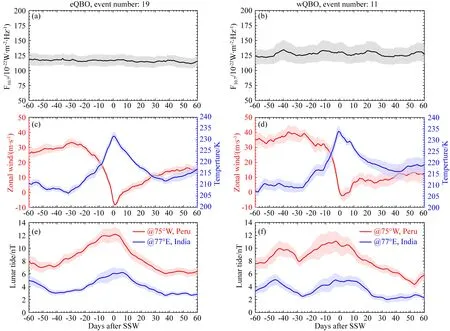
图5 格式与图4一致,但是左图为eQBO,右图为wQBOFig.5 The same as Fig.4, but SSW is classified as eQBO (left) and wQBO (right)
3.2 幅度峰值的经度差异
EEJ的经度差异通常与电离层电导率和非迁移潮汐波等因素有关(Rastogi, 1962;Doumouya et al., 2003; England et al., 2006; Lühr et al., 2008).尽管EEJ中M2分量的幅度的经度差异与EEJ的经度差异不同,但是在春秋分EEJ中M2分量的经度差异依然与背景磁场的强度存在的很好的相关性,这是由于电导率与背景磁场的强度成反比(Yamazaki et al., 2017).由于磁赤道很大一部分在海洋上,因此可利用的地磁台站数据非常有限,利用其统计SSW期间EEJ中M2分量的强度的经度变化也很困难.磁场卫星数据给我们提供了新的机会,在图1c和图2c中,卫星数据和地磁台站数据得到的结果基本一致,这意味着可以利用卫星数据来研究EEJ中M2分量的经度变化.
为了研究SSW期间EEJ中太阴半日潮汐幅度的峰值与背景磁场的关系,我们给出了IGRF磁场随地理经度的变化(图6),以及SSW期间不同经度带EEJ中M2分量的变化情况(图7).我们选取的经度带为0、75°E、140°E、140°W和75°W,分别用红色、绿色、蓝色、黑色、青色表示.由图6可知,磁场强度由强到弱分别为75°E、140°E、0°、140°W和75°W,电导率的强弱次序与背景磁场相反.如果SSW期间太阴半日潮汐的峰值强度变化与电导率一一对应,那么其峰值强弱顺序也该如此.在图7中,太阴半日潮汐峰值由强到弱分别是75°W,140°W、140°E、75°E和0°.很明显西半球的太阴半日潮汐峰值要比东半球强,磁场最弱的地方M2分量的峰值强度最强,但是在东半球太阴半日潮汐的峰值强度与背景磁强无正相关关系.图7的结果表明,太阴半日潮汐的经度差异可能与背景磁场强度有关,但也有其他影响因素.
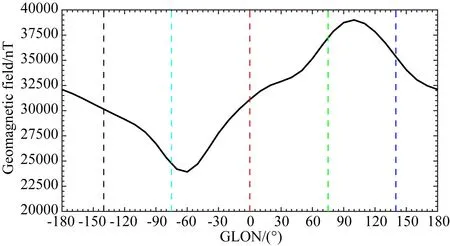
图6 IGRF磁场模型下磁赤道处地磁场强度随经度的变化,其中红、绿、蓝、黑、青色分别代表0°,75°E, 140°E, 140°W, 75°WFig.6 The longitude variation of magnetic field intensity at magnetic equator in the frame of IGRF. Red, green, blue, black, cyan represent 0°, 75°E, 140°E, 140°W, 75°W, respectively

图7 SSW期间EEJ中M2随时间变化图,其中红、绿、蓝、黑、青色分别代表0°,75°E, 140°E, 140°W, 75°W经度Fig.7 Daily variations of lunar semidiurnal tidal amplitude in EEJ from satellite data at different longitude sector during SSW. Red, green, blue, black, cyan represent 0°,75°E, 140°E, 140°W, 75°W, respectively
一般认为,太阴潮汐起源于地球与月球的相互作用,以及海洋的垂直运动.Pedatella等(2012)利用WACCM模型发现太阴半日潮汐在低纬度存在经度变化,而且认为这种经度变化是太阴半日潮汐与静态行星波的非线性作用引起的,而不是海洋潮汐运动.在太阴半日潮汐向上传播过程中,由于不同经度上背景大气条件存在经度差异,因此在E层磁赤道地区太阴半日潮汐峰值也可能存在经度差异(Siddiqui et al., 2017).还有一种解释是EEJ中太阴半日潮汐的经度差异可能与中性风和背景磁场的相互作用有关,也就是说太阴半日潮汐的经度差异可能与赤道电离层E区风发电机效应有关(Siddiqui et al., 2017).电离层电流与U×B的变化有关,Maute等(2015)利用TIME-GCM研究了磁场和中性风对SSW期间E×B的经度变化的影响,他们认为在SSW期间E×B漂移峰值时间往午后移动的经度差异主要是由中性风引起的.另一方面,非迁移潮汐波在太阴半日潮汐波的经度变化中也扮演着非常重要的作用(Yamazaki et al., 2017).利用迁移潮汐波模来激发太阴半日潮汐,很难得到太阴半日潮汐的经度结构,只有迁移潮汐波模和非迁移潮汐波模同时存在,才能够复现太阴半日潮汐的经度结构,其中在冬季电离层E区高度上SE2和SW4在对于太阴半日潮汐经度结构的形成有显著的重要性(Paulino et al.,2013).此外,太阴半日潮汐的幅度还与地理纬度有关,根据hough模的结构,从地理赤道到中纬度地区,大气半日潮汐幅度随纬度的升高而增强,而Huancayo台站的地理纬度高于Tirunelveli台站,因此秘鲁磁赤道半日潮汐大于印度磁赤道的半日潮汐.以往的研究表明冬季南半球得太阴半日潮汐幅度更强(Paulino et al., 2013; Pedatella et al., 2012).对于SSW期间EEJ 中M2分量的经度差异,我们目前很难给出具体的解释,从图6中我们可以认为,太阴半日潮汐幅度峰值的经度差异可能与背景磁场强度有关,但也有其他过程的影响,还需要进一步的研究.
4 结论
本文利用地磁台站水平磁场数据和卫星标量磁场数据,对SSW期间EEJ中太阴半日潮汐的经度变化进行了统计学研究,揭示了它们存在的经度变化,并分析了太阴半日潮汐达到峰值的时间和强度的经度差异的影响因素和可能原因,得到了如下主要结论:
(1)SSW期间,印度扇区和秘鲁扇区EEJ中太阴半日潮汐均存在明显的增强,但是达到峰值的时间和强度存在差异.
(2)SSW期间EEJ中太阴半日潮汐达到峰值的时间与太阳活动有关.太阳活动低年,印度扇区和秘鲁扇区的EEJ中太阴半日潮汐达到峰值时间的经度差异小于太阳活动高年.在印度扇区,不同太阳活动水平EEJ的太阴潮汐达到峰值时间基本不变,而秘鲁扇区太阳活动高年时EEJ的太阴半日潮汐的峰值时间比低年早.
(3) SSW期间EEJ中太阴半日潮汐达到峰值的时间与QBO相位有关.QBO东相位时,印度扇区和秘鲁扇区的EEJ中太阴半日潮汐达到峰值时间的经度差异较小于QBO西相位时.印度和秘鲁扇区QBO西相位时EEJ中太阴半日潮汐峰值时间早于QBO东时.
(4)通过对比不同地理经度磁赤道地区主磁场强度与SSW期间EEJ中的太阴半日潮汐峰值幅度的对应关系,我们发现秘鲁扇区的太阴半日潮汐的峰值强度高于印度扇区,这可能与背景磁场强度有关.但背景磁场强度并不足以解释太阴半日潮汐强度在其他经度带的差异,还存在其他的影响机制.
致谢本研究中所用的太阳活动指数可以从OMNIWeb网站获取(https:∥omniweb.gsfc.nasa.gov/form/dx1.html),平均纬向风和平均纬向温度的再分析数据可以从欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts)网站获取(https:∥www.ecmwf.int/),CHAMP卫星标量磁场数据可以从http:∥doi.org/10.5880/GFZ.2.3.2019.004 网站获取,SWARM卫星标量磁场数据可以从ftp:∥swarm-diss.eo.esa.int网站获取,而TIR、TRD、ABG和FUQ台站水平磁场数据可以从世界地磁数据中心爱丁堡站下载(http:∥www.wdc.bgs.ac.uk/data.html),HUA台站水平磁场数据有德国地学中心数据提供(https:∥dataservices.gfz-potsdam.de/portal/index.html),感谢上述机构或网站对本文的数据支持.

