生成式对抗网络在手写字的性能分析

张立，李林，郭春阳，钟小华

（广东白云学院机电工程学院，广州510450）

0 引言

随着大数据时代的到来，互联网上的数据资源越来越多，其中图片类数据资源为基于大数据集的深度学习算法提供了重要的训练样本。2012年Krizhevsky等人提出AlexNet［1］基于卷积运算的深度学习网络，在ImageNet LSVRC-2010竞赛中取得冠军，并且识别精度高于第二名10.9%，成为卷积神经网络（convolutional neural network，CNN）在图像识别领域的重要模型；之后更有VG⁃GNet系列模型［2］、Inception模型［3］、ResNet系列［4］等优秀的卷积神经网络不断刷新ImageNet数据集的成绩，更进一步推动深度卷积神经网络的发展。Ian J.Goodfellow等人于2014年10月提出了通过对抗过程估计生成模型的新框架，即生成式对抗网络（generative adversarial networks，GAN）［5］，作为一种新型无监督学习的方法。2016年Alec Radford等人提出DCGAN［6］模型，将CNN融入到GAN，从大量的无标记数据中学习特征对图像进行分类，使模型具有较强的表达能力；同年Xi Chen等 人提出Info GAN［7］模 型，将信 息 理论与GAN相结合使输入样本更具有可解释性；2017年Lon Bottou等人提出Wasserstein GAN［8］，通过裁剪判别式网络的梯度，使GAN训练起来更加容易收敛，生成模型产生的图片质量更高。目前生成式对抗网络除了应用在机器翻译，主要应用于图像生成，如超分辨率任务、语义分割、数据增强等任务。

1 GAN

生成式对抗网络是集生成模型和判别模型于一体的机器学习网络，此模型不依赖先验假设而完成，网络结构如图1所示。生成模型的核心思想是通过已知数据集训练随机噪声从而产生指定大小、风格的图片，判别模型依据真实数据对生成模型产生的新图片进行判别，生成模型尽可能的欺骗判别模型，从而形成一个动态博弈［9］的网络。生成模型生成的伪样本尽可能与真实数据相似，判别式模型通过交叉熵损失函数对伪数据和真实数据进行计算。交叉熵损失函数如公式（1）所示。

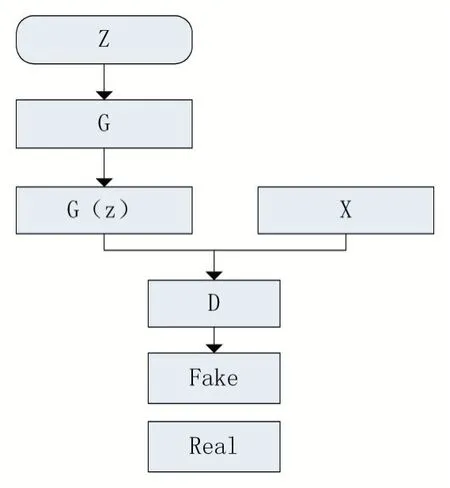
图1 GAN网络结构

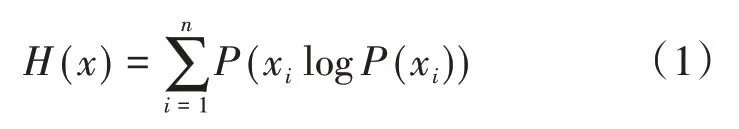
式中：P(xi)为xi事件发生的概率。

生成式对抗网络的两个模型通过损失函数联系起来，在模型训练过程中动态调整二者隐藏层的参数，将两个模型的损失函数之和作为总的损失函数进行训练。在训练过程中，D(x)判别输入数据的真伪并计算相应的概率值，生成式模型G(z)生成的图片尽可能使D(G(z))的值小，从而V(D,G)也会变得很小，使用实际梯度下降算法作为该损失函数的优化器。

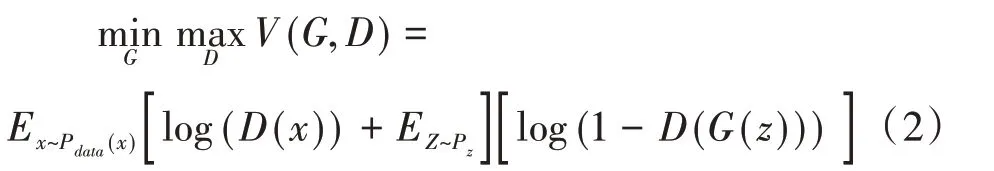
式中：D(x)为判别器，计算图片为真的概率值，G(x)为生成器，Pdata(x)服从高斯分布。

图2为GAN模型损失函数和训练生成图片，基于GAN模型生成的数据较为模糊，图片中的噪声较多；生成式模型和判别式模型的损失函数在训练过程中不稳定，迭代750~1 000次时损失函数发生较大波动。主要原因是使用交叉熵作为损失函数，不能很好的度量数据分布不一致的数据，使得迭代初期损失函数值较大，影响训练速度和效果。

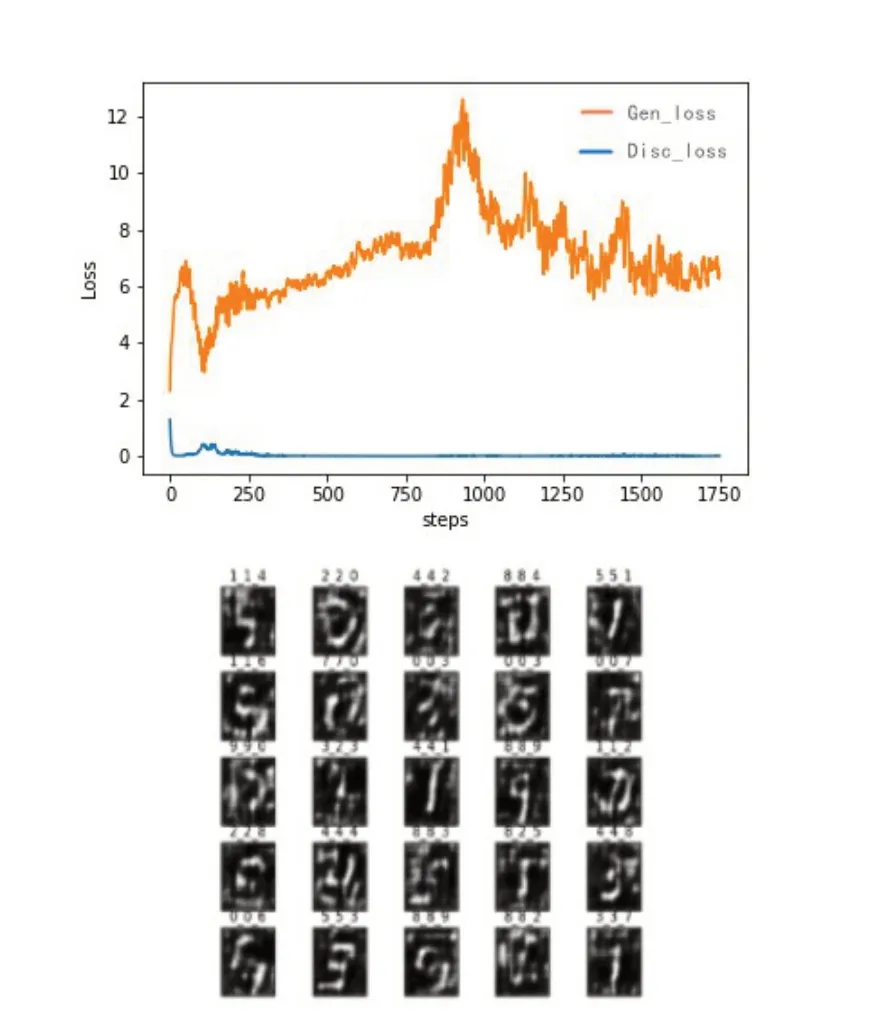
图2 GAN损失函数和生成数据

2 Info GAN

原始GAN网络通过生成器模型拟合训练集的数据真实分布，迭代过程中学习训练集的边缘、颜色等语义特征，但是随机噪声z与生成图像的特征是否相关、分布是否一致却是未知的，致使原始GAN模型不能有效的对卷积运算生成的特征进行编码。信息最大化生成对抗网络（information maximizing generative adversarial nets，Info GAN）能够学习离散数据与连续数据之间的互信息，影响生成器的输出变量。Info GAN模型把生成器的噪声分为两部分，分别是固定噪声z和隐变量c。隐变量c为先验概率分布，可以用来生成数据的不同特征。在Info GAN网络中约束隐变量c，隐变量c对于生成新的数据G（z，c）具有可解释性，则c与G（z，c）具有较高的相关性。随机噪声经过生成器输出图片，隐变量c的信息损失大小影响图片生成的质量，因此在Info GAN模型中，损失函数定义为隐变量c与生成器之间的互信息［10］，如公式（3）所示。Info GAN网络结构如图3所示。

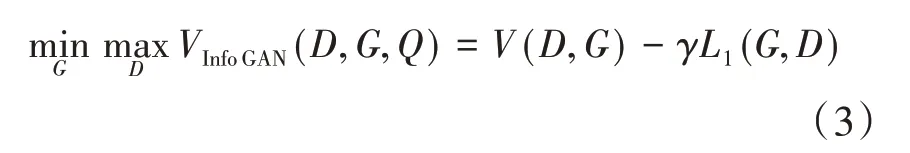
式中：G、D分别为生成器和判别器，γ为正则化系数。

图3 Info GAN网络结构

由图3可知，隐变量c与噪声z共同作为生成器的输入数据，通过变分推断思想模拟真实数据的分布，迭代计算最优互信息下界实现模拟真实数据分布，在图向量中保留更多的隐变量c，并在生成器中计算二者的互信息。生成器产生的图片与真实图片共同作为判别器的输入，从而使判别器和生成器同时更新参数，新生成的图片与真实图片更加相似。将Info GAN应用在Mnist数据集，其损失函数与生成数据如图4所示。

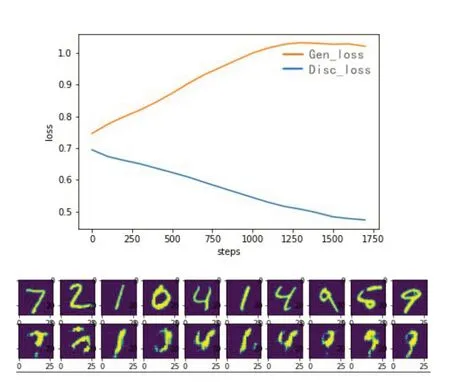
图4 Info GAN损失函数与生成数据

图4中生成式模型损失函数与判别模型损失函数随着迭代次数的增加，函数曲线没有尖锐的抖动，且有逐渐降低的趋势。生成式模型的损失值分布在0.73~0.97之间，损失值比较小，生成的新数据效果清晰、风格多样。

3 WGAN-GP

WGAN模型对GAN的损失函数进行改进，作者发现交叉熵损失函数不能衡量两个不相交部分数据的分布距离，导致GAN训练不稳定。因此作者用李普西斯条件代替交叉熵作为损失函数，将反向传播更新后的权重强制截断到一定范围内，满足李普西斯连续性条件。WGAN去掉GAN网络中的激活函数层，并且对生成器和判别器色损失值不再取对数。在一定程度上使GAN模型训练变得稳定，但是经过剪切后的权重被限制在一定的范围内，不能充分发挥深出度卷积神经网络的拟合能力，其权重分布如图5所示。

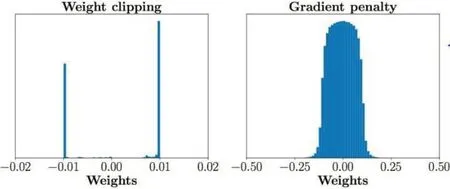
图5 裁剪后的权重分布

WGAN-GP模型与WGAN采用同样的网络结构，仅对损失函数进行改进，采用Earth-Mover（EM）距离。WGAN-GP对每一批次中的样本进行采样，计算判别器的梯度与其限制梯度k之间建立二范数损失函数，对更新后的权重进行惩罚。WGAN-GP的损失函数如公式（4）所示。

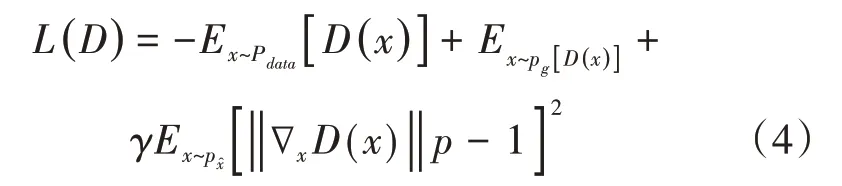
WGAN-GP通过连续性限制条件惩罚梯度，解决训练模型出现的梯度爆炸问题，比WGAN更容易收敛，增加数据分布的任意性，使生成的样本质量更高。WGAN-GP损失函数以及生成数据如图6所示。

WGAN-GP模型的损失函数曲线在迭代初期有较大的波动，随机噪声数据分布与训练数据集的分布不一致，初期损失之较大。迭代过程中出现较大的波动，迭代1500次以后，两条损失函数曲线趋向收敛，缘于在损失函数增加惩罚权重，使模型保持稳定。生成器产生新的数据较为清晰，但是部分数据训练不完整，与训练集中数据相差较大。

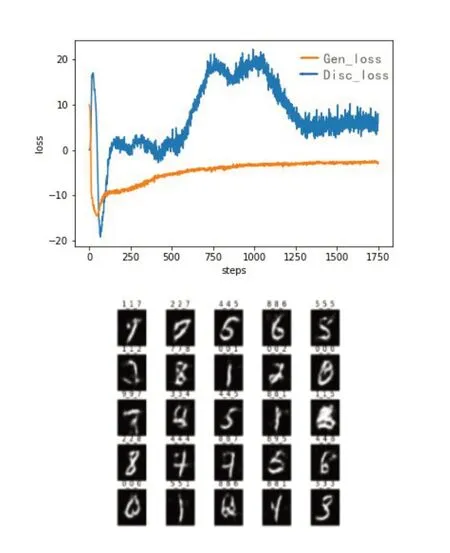
图6 WGAN-GP损失函数与生成数据

4 DCGAN

深度卷积生成对抗网络（deep convolutional generative net，DCGAN）模型采用CNN作为Gener⁃ator和Discriminator的网络骨架，以CNN作为特征提取，使模型具有更强的表达能力，有效的保留图向量的语义信息；DCGAN模型更加注重在未标注的数据集上学习有利于数据生成与识别的特征表示，生成的图片质量更佳。DCGAN网络结构如图7所示。

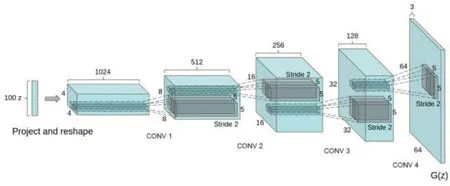
图7 DCGAN网络结构

DCGAN模型相对于GAN模型在网络结构上进行了改进，使用步长卷积代替了上采样层，卷积可以更好的提取图像特征，并且网络采用全卷积形式，舍弃全连接层而提升模型的收敛速度；生成器和判别器的每一卷积层均使用了归一化函数，提升模型的训练速度和稳定性；在训练过程中采用异步训练方法，固定判别器，模型对生成器进行训练，使得二者达到动态平衡。使用Adam优化器对损失函数进行优化，其中学习率设置为0.0002达到最好的训练效果。DCGAN的生成器和判别器分别采用ReLu和Leaky ReLu作为激活函数，减少梯度消失。ReLu和Leaky ReLu激活函数分别如公式（5）、（6）所示。

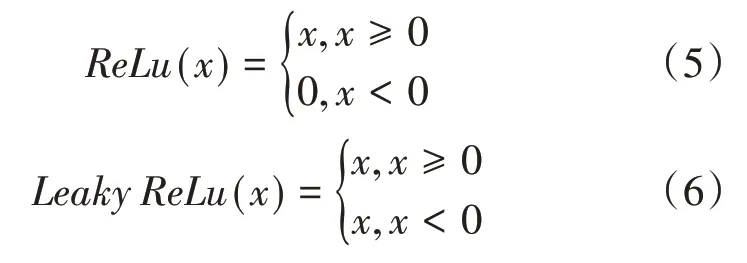
DCGAN模型在Mnist数据集的损失函数如图8所示。

图8 DCGAN损失函数与效果

DCGAN的模型判别模型和损失模型的损失函数随着迭代次数的增加而出现较大的波动、不稳定现象，损失曲线不稳定即模型未能收敛。右图为生成式模型产生的新图片，经过1750次迭代，部分图片质量较好，部分图片未能形成真正有效的新数据。

4 结语

通过对比试验发现，Info GAN模型的损失函数极值小于1.0，GAN、WGAN-GP、DCGAN等模型的损失曲线极值均大于Info GAN模型的最大值。生成式模型产生的图片，Info GAN模型产生的图片较为清晰、噪声较少，图片中的数据较为完整。四种模型产生不同效果的图片，主要源于网络结构、损失函数的不同。Info GAN通过计算隐变量与生成式模型之间的互信息，直接影响到其输出，使得模型具有可解释性，随机噪声可以模拟训练数据集的分布；其余三个模型再网络结构上较为相似，且损失函数衡量相关性较小的数据集时效果较差，导致损失值和图片质量不如In⁃fo GAN模型。因此，基于互信息的损失函数可以使模型损失函数降低，提升模型的训练效率，生成图片更清晰、完整。