一种求解n皇后问题的概率回溯复合算法
徐少飞,张立臣,李鹏
(陕西师范大学计算机科学学院,西安 710119)
0 引言
八皇后问题是指在一个8×8的国际象棋棋盘上随机摆放八个皇后[1],使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,要求求出所有的可行解。一个八皇后问题的可行解如图1所示。
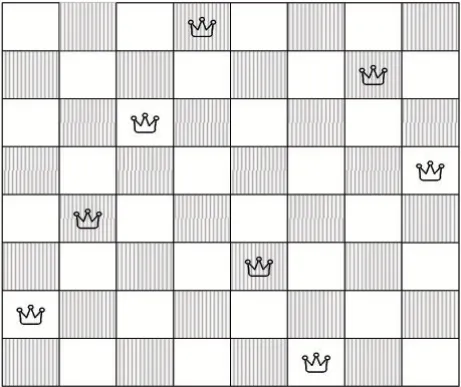
图1 八皇后问题的一个可行解
n皇后问题是八皇后问题的推广,是指在一个n×n的棋盘上放置n个皇后,使任意两个皇后不能相互攻击。我们知道,传统的回溯算法可以求解n皇后问题,但其时间复杂度是指数型的,算法效率较低。目前不少学者对传统回溯算法进行改进,文献[2]利用了n皇后问题解的对称性质对回溯法进行了改进,但优化效果并不明显;文献[3]和文献[4]利用基于位运算的回溯算法进行求解,在整个解空间中搜索,仍没有降低算法的时间复杂性。为了研究更高效、简洁求解n皇后问题一组可行解的算法,本文将传统的回溯算法与概率算法相结合,将棋盘分割为两部分,前半部分使用概率算法求解,后半部分采用回溯算法求解,并合理设置影响算法性能的分割系数和回溯方式。实验结果表明,相比于传统的回溯算法,该算法能够有效地缩短求解时间,因而可以极大拓展在规定时间内可求解问题的规模。
1 n皇后问题求解模型的建立
约定第i个皇后放在棋盘的第i行,设其所在的列为xi(i=1,2,3,…,n),这样问题的解就是n个皇后所在列的序号组成的一个n元一维向量(x1,x2,x3,…,xn),解空间是从1到n的全排列。约束条件是这n个皇后在棋盘上的位置(1,x1),(2,x2),(3,x3),…,(n,xn)不在同一列和同一对角线上。
即对于任意两行i和j上的皇后,需要满足的约束条件有两个:①不在同一列:xi≠xj;②不在同一对角线上:abs(xi-xj)≠abs(i-j)。
2 回溯法求解n皇后问题
2.1 算法思想
回溯法的基本思想是,按照顺序依次确定每个皇后的位置,首先将第一个皇后放置在满足约束条件的第1个位置,即x1=1,然后再为下一个皇后确定合适的位置,以此类推,直到确定了所有皇后的位置。在这一过程中,可能会出现这样的情况:即无法为第n个皇后找到满足约束条件的位置。这说明其前面已放置皇后的位置需要进行调整,因此可以先考虑将第n-1个皇后移至下一个满足约束条件的位置,如果第n-1个皇后无法寻找到下一个满足约束条件的位置,则可以进一步向前调整第n-2个皇后的位置,以此类推。之后再为第n个皇后寻找满足约束条件的位置。以这样的方式进行下去,最终可以保证所有皇后在互不攻击的情况下放置在棋盘中。
2.2 算法求解
2.2.1 递归回溯算法
递归回溯算法的思想是基于深度优先搜索策略[5]。对于n皇后问题,递归的回溯算法采用递归的方式依次确定每个皇后的位置,若一个皇后的所有位置都不满足约束条件,算法将回溯至前一个皇后。
算法1运用递归回溯法解决n皇后问题伪代码描述


2.2.2 非递归回溯算法
求解n皇后问题的非递归回溯的算法同样采用深度优先搜索策略,并在不符合约束条件时及时回溯[6-7]。相比于递归的回溯算法,非递归回溯算法不需要频繁地调用系统堆栈,而是在一个数组中进行回溯的,从而节省了系统资源。
算法2运用非递归回溯法解决n皇后问题伪代码描述


2.3 算法分析
回溯法基于深度优先搜索的策略在整个解空间中进行搜索,并在不满足条件时及时进行剪枝操作。在解决n皇后问题的过程中,若不进行任何的剪枝操作,最坏情况下,其时间复杂度可达O(nn),属于指数级别。相比于一般的穷举法,回溯算法虽然避免了一些不必要的搜索,并可将最坏情况下的时间复杂度优化至O(n!),但其时间复杂度仍然较大,性能不好。
3 拉斯维加斯概率算法求解n皇后问题
3.1 算法思想
拉斯维加斯(Las Vegas)概率算法的基本思想是用生成的随机序列代替有次序的穷举,然后判断基于该随机序列所产生的结果是否为符合问题约束条件的正确解[8]。拉斯维加斯概率算法非常适合于在一个问题解空间中寻找一个可行解的场景。但是,该算法同时具有一定的缺点,即存在无法找到可行解的情形。事实上,出现这种情况的可能性不大,而且我们可以通过增加算法执行次数的方式进一步提高找到可行解的概率。
我们知道,当程序重复执行的次数越多,运行时间越长时,利用拉斯维加斯概率算法求得问题的一个可行解的概率也就越大[9-10]。因此,如果要使求解问题失败的概率降至任意小,可以足够多次地重复调用拉斯维加斯概率算法进行求解。
3.2 算法分类
为了表述方便,本文将拉斯维加斯概率算法分为拉斯维加斯循环算法和拉斯维加斯一般算法。
拉斯维加斯循环算法的成功率是100%,它将循环执行,直到找到一组可行解时退出程序。
拉斯维加斯一般算法的成功率不是100%,它将设定一个最大循环次数k,然后再进行有限次数的循环,直到找到一组可行解或当循环次数>k时,结束程序。
3.3 算法求解
对于n皇后问题,我们目前无法确定每个皇后放置的具体规律,因而无法快速地放置这些皇后,这使得我们可以采用随机放置的方式。这种随机放置的思想与拉斯维加斯概率算法相同。该算法依次随机地放置每一个皇后,直到所有的皇后均已在满足约束条件的情况下放置好。在放置当前皇后的过程中,需要保证:新放置的皇后与前面已放置好的所有皇后不冲突。
本文将选择拉斯维加斯循环算法来解决n皇后问题,确保其正确率达到100%,方便后续进行各种算法运行时间的比较分析。
算法3运用拉斯维加斯概率算法解决n皇后问题伪代码描述
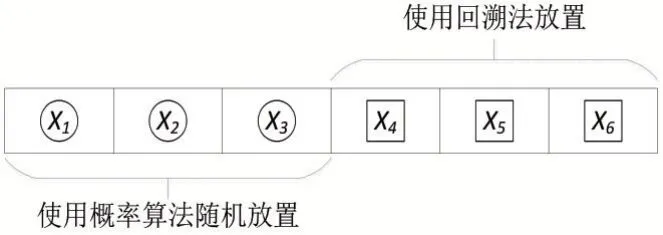
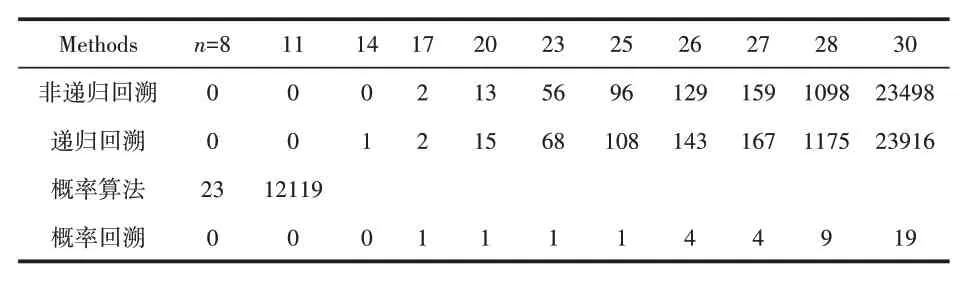
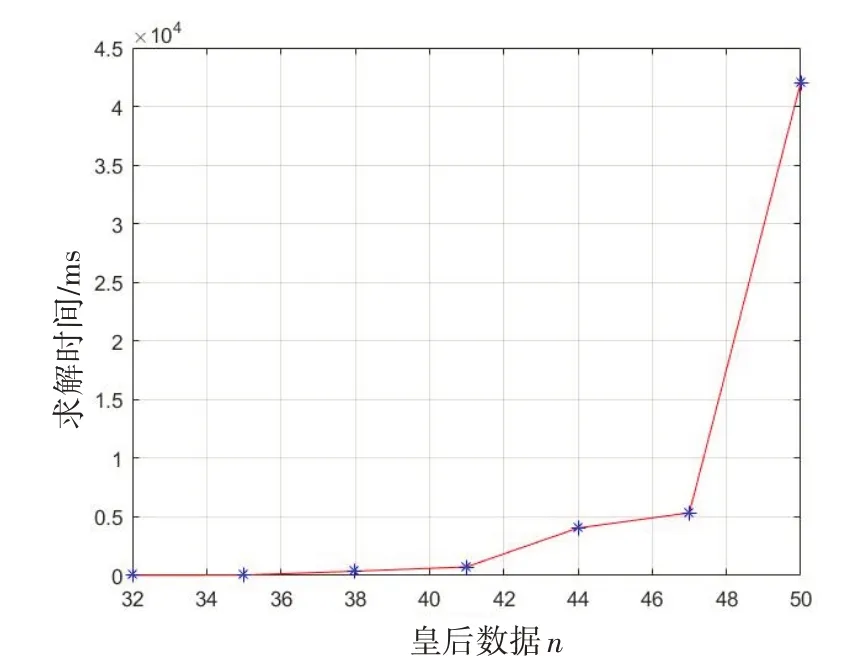
Input:开始进行概率算法的行序号star(t0 对于拉斯维加斯概率算法,假设一共要排列n个皇后,每一行的皇后平均要进行k次测试才能找到合适位置,LV函数的算法时间复杂度为O(n),在Probability函数中,LV函数将被执行k次,因此,最终该算法的时间复杂度应为O(n×k)。 分析上文中概率算法和回溯算法的特性可知,概率算法在问题规模较小时可以快速得到一个可行解;而回溯算法则可以利用其回溯的特性保证能够求得问题的一个可行解[11-12]。因此,我们可以将二者的优势相结合,提出一种概率回溯复合算法。该算法具体为:先将整个棋盘分为两部分,然后在前一部分采用拉斯维加斯概率算法随机地放置皇后,在后半部分使用回溯算法放置剩余的皇后,直到所有皇后都被放置完毕,如图2所示。 图2 概率回溯复合算法示意 设皇后数量为n,d为分割系数,用于分割棋盘,floor为向下取整函数。在棋盘的前floor(n×d)行采用拉斯维加斯概率算法随机放置皇后,后续的行采用非递归回溯的算法放置其余皇后。 为了确保该算法的成功率为100%,本文将在棋盘的前floor(n×d)行采用拉斯维加斯循环概率算法进行求解,并允许后续行在使用回溯法时能够回溯到棋盘首行。 算法4运用概率回溯复合算法解决n皇后问题伪代码描述 Input:皇后数量n,分割系数d,开始进行概率算法的行序号start(0 当皇后数量为n时,则先在棋盘前floor(n×d)行使用拉斯维加斯概率算法,在后续行使用非递归回溯算法,采用概率算法的时间复杂度为O(d×n×k),使用回溯法的 时 间 复 杂度为O((d×n)!)。 本文实验环境:CPU,Intel Core i5-8265U;内存容量,8.00 GB;硬盘,1 TB;PF使用率,47%~50%;集成开发工具,Eclipse 4.12.0。 输入数据为皇后的数量n,这也决定了棋盘是一个n×n大小的。本实验将n分别取为8、11、14、17、20、23、25、26、27、28、30,概率回溯复合算法的分割系数d取为0.5,然后测试四种算法的运行结果及运行时间。在特定输入规模n的情况下,每一种算法运行20次,运行时间取这20次实验运行时间的平均值。 分别对n皇后问题递归回溯、非递归回溯、拉斯维加斯概率、概率回溯复合算法的算法规模和执行时间进行仿真。四种算法的成功率为100%,其求解时间如表1所示。 表1 四种算法求解时间(单位:ms) 当n>11时,拉斯维加斯概率算法的求解时间就已经超过了10000 ms,因此不再统计概率算法后期的求解时间。 从表1中可以直观地看到四种算法的求解时间对比,当n从27变到28时,两种回溯算法的求解时间的增长速度很快,当n从28变到30时,其求解时间更是呈指数形式增长。相比之下,概率回溯复合算法的求解时间一直都较短,并且随输入规模n增加而增长的速度也十分缓慢。 传统的回溯算法在n=30的时候求解时间就已经很长了,考虑到计算机的算力瓶颈,后面只观察随着n值的继续增大,概率回溯复合算法求解时间的增长情况。 图3 概率回溯复合算法求解时间(n值:32~50) 图3是当n值从32变化到50的过程中,概率回溯复合算法求解时间的变化情况。当n值达到41后,算法的求解时间就增长的比较快了,当n值从47到50的时候,算法的求解时间增长得最快,在n=50时,算法求解时间就已达到了42047 ms。这可能是由于前半部分的概率算法和后半部分的回溯算法需要花更多的时间去寻找每个皇后的合适位置。 对于概率回溯复合算法,当在前若干行使用完拉斯维加斯概率算法之后,后续行会使用回溯法继续放置剩余皇后。当回溯法需要进行回溯操作时,回溯范围有两种,一种是截止到开始使用回溯算法的那一行;另一种是截止到首行。可通过实验验证的方式对比这两种范围对算法性能的影响。皇后数量n将分别取为7、10、15、18、20、23、25、26、27、28,其概率算法部分采用成功率非100%的拉斯维加斯一般概率算法,最大循环次数k选为10000,这样便于研究不同参数分别对概率算法部分和回溯算法部分的影响情况。 表2 回溯截止到首行的求解情况 表3 回溯截止到开始回溯的那一行的求解情况 表2和表3分别是回溯截止到首行的求解情况和回溯截止到开始回溯的那一行的求解情况。通过两种回溯方式的对比实验,可以知道,采用回溯到首行的方式,算法整体求解的正确率要更高一些。 概率回溯复合算法中的分割系数d表示前floor(n×d)行使用拉斯维加斯概率算法,其中,floor()函数是下取整函数。因此,分割系数d的选取对该算法的性能有重要影响。本次实验,规定采用回溯至首行的策略,概率算法部分采用成功率非100%的拉斯维加斯一般概率算法,设置分割系数分别为0、0.2、0.4、0.6、0.8、1,测试其在n=30的情况下算法连续运行50次能成功求解的概率,图4是求解正确率随分割系数d变化的折线图,测试结果如图4所示。 图4 求解成功率随分割系数d的变化情况 分析图4可知,当分割系数d增大时,算法的求解成功率明显下降。当d=1时,概率回溯复合算法退化为回溯算法,当d=0时,概率回溯复合算法变为拉斯维加斯概率算法。 分割系数除了对算法成功率有很大影响外,还影响算法的求解时间。图5测试在n=30时,算法求解时间随分割系数的变化情况。分割系数d分别取0.2、0.3、0.4、0.5、0.6、0.7、0.8,采用回溯到首行的方式,概率算法部分采用成功率为100%的拉斯维加斯循环概率算法,这样能更合理地统计算法求解时间。 图5 求解时间随分割系数d的变化情况 从图5可知,在分割系数从0.2增加到0.8的过程中,算法的求解时间是一个先减少后增加的过程,在d=0.4时,算法的求解时间最短。在分割系数为0.7和0.8时,程序的运行时间已超过规定的最大时限5 min,因此不再进行计算。 由此可见,选取合适的参数可以使概率回溯复合算法的性能得到很大提升。 本文通过对比实验,发现传统的回溯算法在n=30的时候就需要两万多毫秒才能得到结果,而相比之下,分割系数为0.5的概率回溯复合算法在n值接近50的时候才会消耗相同的时间,这极大地拓展了规定时间内算法可计算和求解的范围。此外,本文还深入研究和分析了回溯方式、分割系数等参数条件对概率回溯复合算法成功率及求解时间的影响,得出了在合理设置这些参数的条件下,概率回溯复合算法在求解n皇后问题一组解上的表现要优于其他算法的结论。这对今后研究与应用该算法以及分析和研究其他NP问题具有较好的指导意义和参考价值。
3.4 算法分析
4 概率回溯复合算法求解n皇后问题
4.1 算法思路
4.2 算法求解

4.3 算法分析
5 仿真实验与分析
5.1 实验环境
5.2 输入数据
5.3 实验结果分析
6 概率回溯复合算法的进一步研究
6.1 回溯范围对算法性能的影响
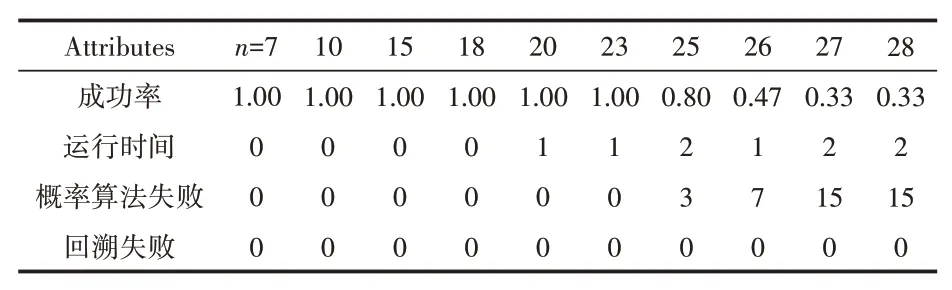
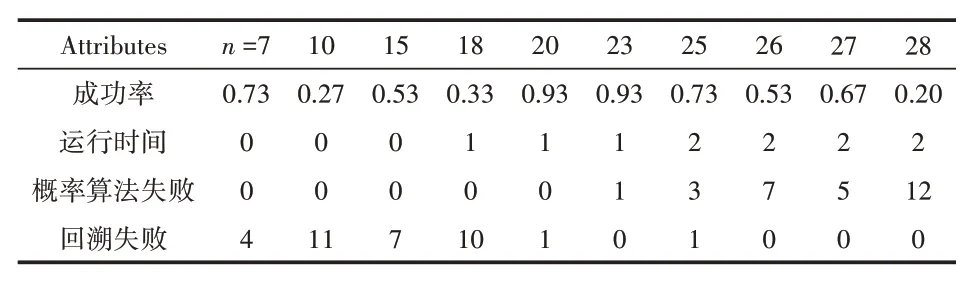
6.2 分割系数对算法性能的影响
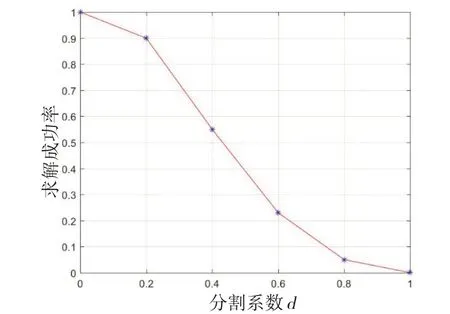
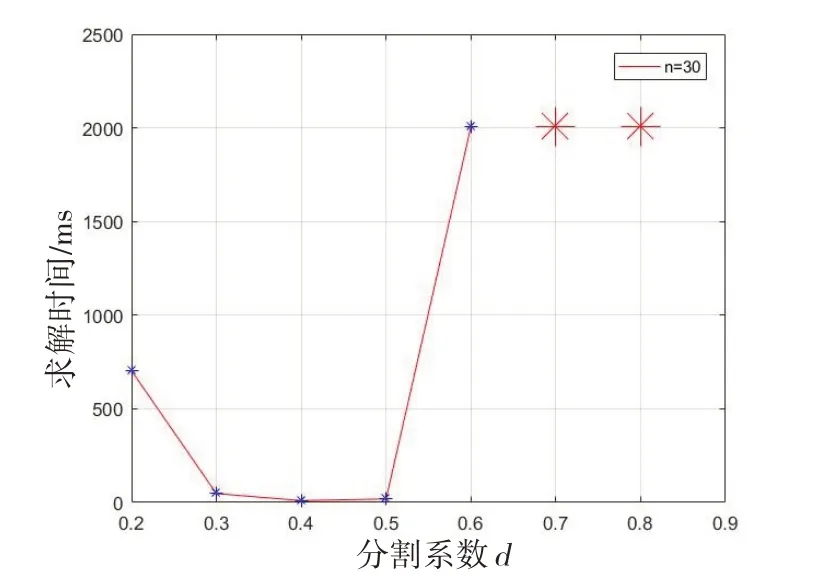
7 结语

