毫米波MIMO 系统中基于自适应梯度算法的混合预编码

张煜，张治，董晓岱

（1.北京邮电大学信息与通信工程学院，北京 100876；2.维多利亚大学电子与计算机工程学院，维多利亚 V8W 3P6）

1 引言

作为5G 及未来移动通信网络的主要技术之一[1-3]，毫米波通信能够提供较宽的带宽，满足高速数据传输需求。然而，高频率、短波长的电磁波具有严重的路径损耗和较差的绕射性能[4-5]，导致通信范围有限。幸运的是，多输入多输出（MIMO,multi-input multi-output）技术可以利用大规模天线阵列来补偿严重的衰减，延长信号的传输距离。

传统的全数字MIMO 架构通常是基于数字预编码器实现的，其中所需射频（RF,radio frequency）链的数量等于天线的数量。射频链通常由混频器、功率放大器和数字-模拟转换器等器件构成。对于毫米波系统，由于过高的功耗和硬件成本[6]，部署全数字预编码具有挑战性。借助毫米波信道的稀疏特性，文献[7]提出了一种混合数字-模拟预编码架构，使用较少的射频链实现低维数字预编码器和高维模拟预编码器的连接，其中模拟预编码器采用模值恒定、相位可调的模拟移相器实现；同时把混合预编码等效为压缩感知中的稀疏信号恢复问题，并使用正交匹配追踪（OMP,orthogonal matching pursuit）算法求解，最终达到了降低功耗和硬件成本的目标。鉴于OMP 算法的计算复杂度较高，有些文献提出了改进算法，包括并行索引选择-忽略矩阵求逆的同步正交匹配追踪（PIS-MIB-SOMP,parallel-index-selection matrix-inversion-bypass simultaneous OMP）算法[8]、基于顺序迭代最小二乘的广义正交匹配追踪（ORLS-gOMP,order-recursive least squares-based generalized OMP）算法[9]、基于正交性的匹配追踪（OBMP,orthogonality-based matching pursuit）算法[10]等。另外，文献[11]根据天线阵列响应矩阵的相关性生成模拟预编码矩阵备选集，有效降低了OMP 算法搜索空间的大小。针对码字搜索问题，文献[12]提出了基于傅里叶变换码本的低复杂度码本搜索方法，降低了搜索复杂度。总体而言，文献[7-11]所提算法都是基于码本的混合预编码方法，所实现的频谱效率还有很大的提升空间[12]。

为了接近最优的频谱效率性能，学者们研究了非码本的混合预编码方案，将混合预编码视作恒模约束下的矩阵分解问题，基于交替最小（AltMin,alternating minimization）算法迭代设计数字预编码器和模拟预编码器。具体地，数字预编码器通过最小二乘准则计算，模拟预编码器的最优解则分别通过共轭梯度（CG,conjugate gradient）[13]、内点法[14]、Barzilai-Borwein 梯度[15]、梯度投影（GP,gradient projection）[16]等算法获得。尽管文献[13-16]提出的非码本混合预编码方案在频谱效率性能上接近全数字预编码，但实现复杂度均较高。虽然文献[13]也提出了一种通过求解正交Procrustes 问题（OPP,orthogonal Procrustes problem）获得混合预编码器的低复杂度算法，但需要假设数字预编码器满足比例酉性质。由于该假设仅在数据流的数目等于射频链的数目时有效[17]，因此当射频链的数目大于数据流的数目时，OPP 算法所实现的频谱效率在一定程度上会有所降低。

上述研究主要针对单用户场景。为了解决多用户场景下的混合预编码问题，文献[18]提出了两阶段混合预编码方案，即基站（BS,base station）首先和移动台（MS,mobile station）联合设计最优的模拟预编码器和组合器以使信道增益最大化，然后设计迫零（ZF,zero-forcing）数字预编码器以减少MS间的干扰。文献[19]提出了一种混合最小均方误差（MMSE,minimum mean-squared error）预编码方法，即每个MS 首先独立配置模拟组合器，然后由BS为所有MS 设计模拟预编码器和数字预编码器。文献[20]提出了一种混合块对角化（BD,block diagonalization）预编码方法，该方法首先设计模拟预编码器和组合器以最大化阵列增益，然后在等效基带信道上应用BD 方法设计数字预编码器。然而，文献[18-20]所提方案获得的频谱效率与全数字预编码相比尚有很大的差距。另一方面，文献[13-16]中的CG-AltMin、BB-AltMin、GP-AltMin 等非码本混合预编码方案同样也可应用于多用户场景，但复杂度较高的问题依然存在。

近年来，深度学习在混合预编码问题中的应用受到了广泛关注[21-28]。从所采用网络模型的角度，基于深度学习的混合预编码方案分为基于实数神经网络的混合预编码[21]、基于复数反向传播（BP,backpropagation）神经网络的混合预编码[22]和基于复卷积神经网络的混合预编码[23-28]三类，其中文献[21]将实数神经网络应用于混合预编码器的设计，文献[22]提出了基于复数BP 神经网络的混合预编码方案，文献[23-28]分别提出了基于ComcepNet、等效信道-卷积神经网络（CNN,convolutional neural network）、CovNet、CNN-MIMO、HPNet 和深度学习量化相位网络模型的混合预编码机制。

进一步地，还可从学习方式的角度，将上述基于实数神经网络的混合预编码和基于复卷积神经网络的混合预编码归纳为线下学习方案，将基于复数BP 神经网络的混合预编码归纳为在线学习方案。线下学习方案分为线下训练和线上测试2 个阶段，在线下训练阶段，随机生成大量信道训练样本，以信道参数为网络输入，以每个信道条件下相应的最佳模拟预编码器或组合器为网络输出，执行训练过程获得网络配置参数；在线上测试阶段，将信道测试样本输入配置好的网络，获得该信道条件下相应的最佳模拟预编码器或组合器，然后，数字预编码器通过对等效信道进行奇异值分解或运用ZF 准则获得。

在训练好网络模型之后，线下学习方案能够快速响应信道参数，获得相应的最佳模拟预编码器或组合器。然而，为了获得最佳的网络配置参数，线下训练阶段往往需要庞大的训练样本，以提高精确度。另外，训练好的网络模型往往针对具体的参数设置，在单用户场景下是具体的发射和接收天线数，在多用户场景下是基站的天线数和用户数。当天线数或用户数发生变化时，需要重新训练以保证网络模型的准确性，这会造成较大的训练开销和较长的训练时间，使算法效率降低[29]。

与线下学习方案形成鲜明对比的是，在线学习方案所需训练样本较少，能够根据信道条件的变化实时地调整网络权值，最佳的数字预编码器和模拟预编码器从网络权值中提取。研究线下学习方案的文献相对较少，以文献[22]为主要代表，其针对多用户场景，提出了基于复数BP 神经网络的混合预编码方案，以最优ZF 数字预编码器和实际混合预编码器之间的最小均方误差为损失函数，采用动量梯度下降（GDM,gradient descent with momentum）算法对网络进行训练，获得的权值即混合预编码矩阵的组成元素。然而，文献[22]没有考虑模拟预编码器的恒模约束，通过训练得到的和模拟预编码器对应的权值没有归一化为统一的模值，这与实际的硬件设计不符。当考虑模拟预编码器的恒模约束时，文献[22]采用的算法收敛速度较慢。

受上述讨论的启发，为了降低现有的传统非码本混合预编码方案和在线学习方案的复杂度，本文针对毫米波大规模MIMO 系统，分别提出适用于单用户场景和多用户场景的低复杂度在线学习混合预编码方案，所需训练样本较少，训练速度较快。本文所提混合预编码方案具体如下：在单用户场景下，提出一种新颖的等效神经网络架构，将数字预编码器和模拟预编码器的每个元素视为单隐藏层神经网络的参数，并将混合预编码器的求解视作该神经网络的参数训练过程；进一步地，设计适用于该等效神经网络的参数训练方法，提出一种基于自适应梯度反向传播（AG-BP,adaptive gradient backpropagation）的混合预编码算法，以最小化损失函数为目标，通过迭代最终获得单用户场景下的最优混合预编码器；最后将所提算法扩展至多用户场景，获得多用户场景下的混合预编码方案。仿真结果表明，在单用户场景和多用户场景下，所提算法实现的频谱效率均接近全数字预编码，且复杂度低于现有的基于交替最小算法的混合预编码方案和基于GDM 的在线学习混合预编码方案。

2 系统模型

本节首先给出单用户场景下的系统模型，多用户场景下的系统模型将在3.5 节给出。考虑一个单用户毫米波MIMO 系统，设该系统中发射机配置Nt根天线、个射频链，接收机配置Nr根天线、个射频链，它们之间通过NS路数据流进行通信。

毫米波传播过程中过高的路径损耗造成散射体有限，毫米波信道通常采用基于扩展Saleh Valenzuela 模型的簇信道模型，信道矩阵H被描述为Ncl个簇的组合，每个簇包含Nray个射线[7]。因此，H可表示为

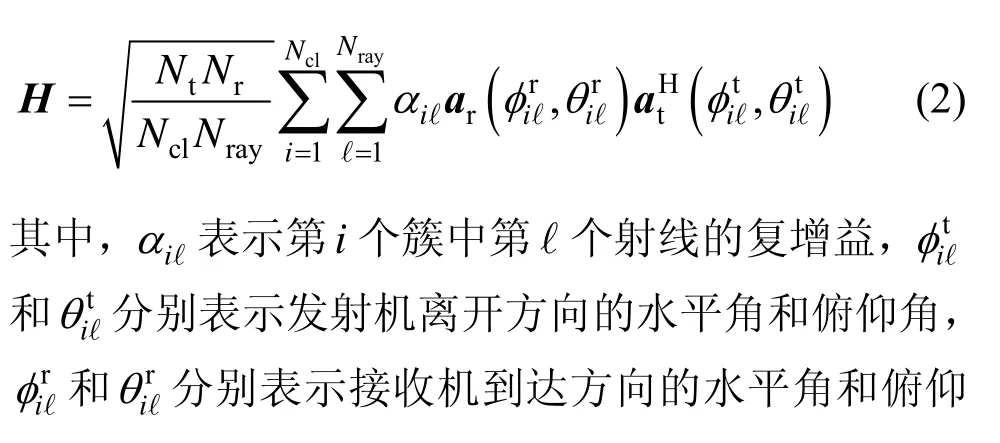
其中，λ为载波波长，d为相邻天线间距离，ny=0,…,Ny-1和nz=0,…,Nz-1分别为天线单元在y轴和z轴的索引，N=Ny Nz为天线总数。

假设发送信号s服从高斯分布并且满足，其中ρ为平均发送功率。则该毫米波通信系统的频谱效率为

为使如上的系统频谱效率最大化，可对FBB、FRF、WRF和WBB进行联合优化，即

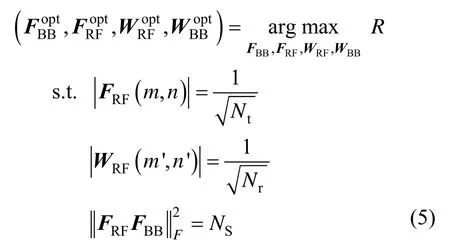
然而，鉴于FRF和WRF的恒模约束，式(5)是不可解的。通过分开设计混合预编码器和组合器，式(5)可以解耦为2 个可解的子问题[7]。最优的模拟预编码器和数字预编码器可以通过求解以下问题获得[13]

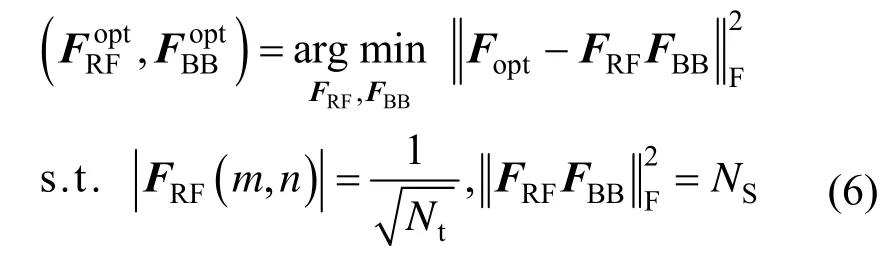
其中，Fopt表示Nt×NS维无约束全数字预编码器，由H的NS个最大奇异值对应的NS个右奇异向量组成。假设H可通过相应的信道估计方法[30]预先获取，定义H的奇异值分解为H=UΣVH，则Fopt=V(:,1:NS)为V 的前NS列元素。

3 算法设计

本节针对单用户场景，首先提出一种描述混合预编码的等效神经网络架构，分析其与传统神经网络架构的不同；然后给出训练数据集的产生方法，并推导出损失函数的表达式；接着以最小化损失函数为目标，提出基于AG-BP 的混合预编码机制；最后针对多用户场景，将所提算法进行扩展，获得多用户场景下的混合预编码方案。

3.1 等效神经网络架构

重新考虑混合预编码式(6)，假设s经过混合预编码处理的信号为那么混合预编码问题可以等效为确定s与y之间的映射关系，即M:s→y。

映射M包含2 个线性组合，即FBB和FRF。因此，混合预编码架构可视为一个单隐藏层神经网络，如图1 所示。

图1 混合预编码的等效单隐藏层神经网络架构

NS路发送信号、个射频链、Nt根发射天线可分别类比成NS个输入层神经元、个隐藏层神经元、Nt个输出层神经元，则输出层信号可以重写为

图1 所示网络的权值dq,u和ap,q（p=1,…,Nt，q=1,…,，u=1,…,NS）与FBB和FRF的每个元n素相对应，可通过训练获得。因此，可以利用神经网络的学习算法[31]来设计混合预编码器。

神经网络的学习过程意味着调整相邻神经元之间的权值以及每个功能神经元的阈值以使网络最优。但本文所提出的混合预编码等效架构与传统的神经网络存在几点不同：1)FBB和FRF的元素均为复数；2) 在混合预编码架构下不存在功能神经元；3) 偏置全为0 且激活函数为恒等函数；4) 最重要的一点是隐藏层和输出层之间连接权存在恒模约束，这使通用的神经网络训练算法不适用于混合预编码器的设计，因此有必要设计混合预编码器专用的权值训练算法。

3.2 训练数据集和损失函数

3.3 基于AG-BP 的混合预编码

在复数神经网络的训练过程中，通常将复数的实部和虚部分别进行更新，然后合并[31]。用字母r和i分别表示复数的实部和虚部，则发送符号权值dq,u和ap,q可写成

第p个输出层神经元的输出为

累积平均误差可重写为

对于ap,q，其增量Δap,q可以写为实部增量Δarp,q和虚部增量Δaip,q相加的形式，即

根据梯度下降法，Δarp,q和Δaip,q沿负梯度方向更新，即

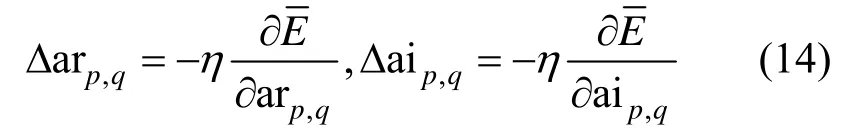
其中，η表示学习率。

根据链式准则，有

将式(15)代入式(13)和式(14)可得

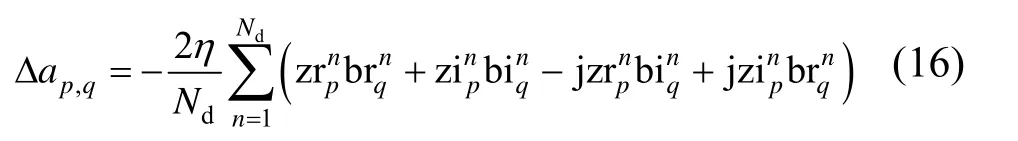
更新ap,q为

为了加速收敛，避免损失函数到达局部极小值，权值增量可基于自适应梯度（学习率）计算[32]，沿负梯度方向的搜索步长与之前所有迭代的梯度值有关，即

其中，δ>0为一个足够小的数值以保证数值稳定性。

考虑到ap,q的恒模约束，重构ap,q为

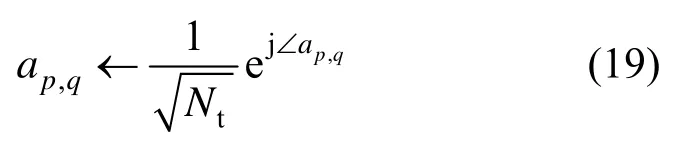
其中，∠ap,q表示复数ap,q的相位。

FRF的每个元素与ap,q一一对应，即

dq,u也可采用与ap,q相似的更新规则。但为了降低计算复杂度，dq,u可直接根据最小二乘解获得

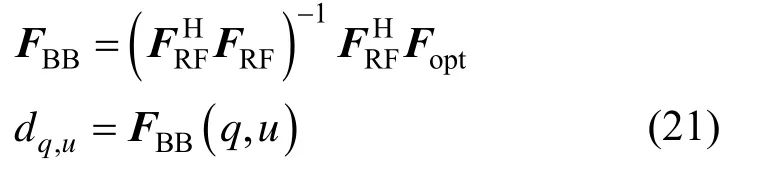
对ap,q和dq,u迭代更新，直到满足以下条件

其中，ε>0为一个足够小的正值；或者当迭代次数超过预定义的最大值tmax时，迭代更新也将停止。最后，更新FBB以满足功率约束

基于AG-BP 的混合预编码算法如算法1 所示。

算法1基于AG-BP 的混合预编码算法

给定无约束全数字预编码器Fopt、训练数据集大小Nd、学习率η和最大迭代次数tmax

接下来，分析算法1 的复杂度。算法1 中每一步操作的复数乘法和除法个数如表1 所示，其中

表1 算法1 每步操作所需复数乘法和除法个数

表示利用初等行变换对m×m矩阵进行求逆所需的复数乘法和除法个数。算法1 和对比算法的计算开销如表2 所示，其中，分别表示内部迭代的总数和外部迭代的个数。对于CG-AltMin、BB-AltMin 和GP-AltMin，为所有外部迭代所需内部迭代个数的累加值。

表2 算法1 与对比算法的计算开销

3.4 基于AG-BP 的混合组合器设计

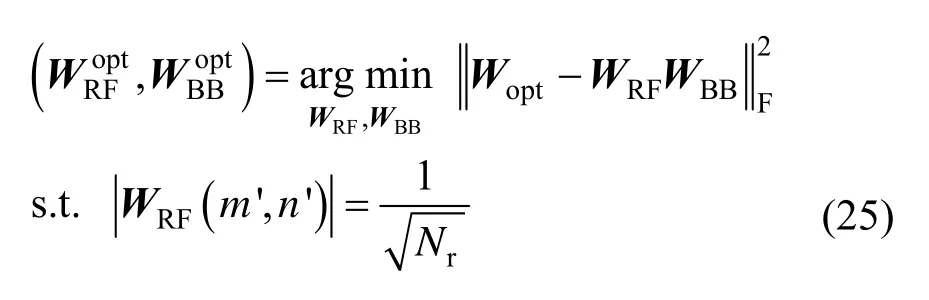
其中，Wopt表示Nr×NS维无约束全数字组合器，由H的NS个最大奇异值对应的NS个左奇异向量组成，即Wopt=U(:,1:NS)。

显而易见，除了功率约束，式(25)和式(6)有相同的形式。因此，可通过把Fopt、FRF和FBB替换成Wopt、WRF和WBB并运用算法1 对式(25)进行求解。

3.5 多用户场景

本节在上述工作的基础上，将所提算法扩展至多用户场景。设配置NBS根天线的BS 同时和U个MS 进行通信，每个MS 均具有NMS根天线。假设每个MS 仅采用模拟预编码架构，即每个MS 仅有一路数据流，则BS 总共有NS=U路数据流。不失一般性，可假设BS 使用NRF个可用数据链中的U个数据链对这U个MS 进行服务，且NRF≥U。在BS 侧，U× 1维发送符号s=[s1,…,sU]T依次经过U×U维数字预编码器FBB=[fBB,1,…,fBB,U]和NBS×U维模拟预编码器FRF的处理，其中，su表示发送给第u个MS 的信号，fBB,u表示与第u个MS 相对应的数字预编码向量。第u个MS 经过NMS× 1维模拟组合器wu处理后的接收信号可表示为

其中，Hu为NMS×NBS维信道矩阵，且与式(2)有相同的表达式；为NMS× 1维高斯噪声向量。则第u个MS 可实现的速率为

其中，ρ表示平均发送功率。

与单用户场景下类似，多用户混合预编码设计的优化目标是最大化所有MS 的和速率，即其中，F和W分别表示模拟预编码向量和模拟组合向量的可能取值所组成的码本。式(28)是一个混整数规划问题，它的解需要搜索整个FU×WU空间的所有FRF和的可能组合。因此，和速率最大化问题的直接解决方案既不实际也不可行。为此，本文提出一种两阶段法，将混合预编码矩阵和模拟组合向量分开进行设计。

具体地，在第一阶段，每个MS 设计各自的模拟组合向量，以最大化信道增益，即

4 仿真分析

本节使用MATLAB 软件对所提算法的性能进行详细的仿真与评估，所用处理器的型号为Intel(R)Core(TM) i5-4210M，主频2.60 GHz，机带RAM 8 GHz。首先考虑单用户场景，设仿真中的发射机和接收机分别具有64 根和16根天线；发射机和接收机射频链个数相等，统一用NRF表示；数据流个数NS=2。毫米波信道的实例依据式(2)和式(3)进行生成，其中簇个数Ncl=5，每个簇的中心到达角和离开角均匀分布在[0,2π)内；每个簇有Nray=10个射线，到达角和离开角服从角度扩展为10°的拉普拉斯分布；第i个簇中第 ℓ 个射线的复增益为，其中表示第i个簇的平均功率。设天线间距d为半波长，噪声功率为1。信噪比（SNR,signal-to-noise-ratio）定义为。ε、δ和tmax分别设置为10-3、10-6和500。以下分析将在随机产生1 000 个信道实例的情况下，将本文算法与传统的OMP[7]、OPP[13]、CG-AltMin[13]、BB-AltMin[15]、GP-AltMin[16]等算法和基于GDM[20]的在线学习方案进行对比。在GDM 中，最大迭代次数和动量因子α分别设置为2 000 和0.9，为区别于本文算法，学习率用μ表示，另外，获得的模拟预编码器通过式(19)进行模值归一化处理。

图2 为NRF=4、SNR=0 时，不同学习率情况下本文算法和GDM 的可实现频谱效率与训练数据集大小Nd的关系。对于BP 神经网络，网络输出与输入的映射关系为非线性函数。对于非线性函数，训练数据集越大，函数的拟合效果越好，训练得到的网络模型才最接近真实函数。

图2 不同学习率情况下频谱效率与训练数据集大小的关系

从图2 可以看到，频谱效率随着Nd的增加而增加，对于本文算法，Nd=3时频谱效率趋于最大值；对于GDM，Nd=4时频谱效率趋于最大值。由此可见，本文算法仅需较少的训练数据集即可达到较满意的结果。在本文算法中，每个权重的搜索步长与之前迭代的一阶导数的平方和有关，仅利用了一阶导数信息即可起到与二阶方法和模拟退火相同的性能，将会使频谱效率收敛到一个稳定值。因此，给定Nd和学习率时，本文算法的频谱效率性能优于GDM。，从图2 中还可以看出，在给出的几个学习率中，η=0.5时本文算法的频谱效率最大，μ=0.9时GDM 的频谱效率最大。

图3 为Nd=3、SNR=0 时不同学习率的收敛情况对比。本文算法的收敛结束条件是式(6)和式(25)中的优化目标趋于最小，等价于使优化式(5)中的频谱效率趋于最大，因此迭代次数会收敛于频谱效率。对于本文算法，η=0.5时的收敛速度较快（平均迭代次数为192，平均收敛时间约为0.131 4 s），且实现的频谱效率较高，平均约为14.58 bit/(s·Hz)；对于GDM，μ=0.9时的收敛速度较快，且实现的频谱效率较高。给定学习率时，本文算法的收敛速度远远快于GDM。从图2 和图3 可以看到，当Nd=3、η=0.5时，本文算法性能最好；当Nd=4、μ=0.9时，GDM 性能最好。因此在后续仿真中，对于本文算法，均令Nd=3、η=0.5；对于GDM，均令Nd=4、μ=0.9。

图3 不同学习率的收敛情况对比

图4 为NRF=4时不同算法的性能对比。根据式(4)，随着SNR 的增加，所有算法可实现的频谱效率均增加。在给定SNR 的前提下，本文算法可实现的频谱效率均高于参与对比的算法，最接近无约束全数字预编码的性能。在本文算法中，经过收敛，模拟预编码矩阵与数字预编码矩阵的乘积FRFFBB接近无约束全数字预编码矩阵Fopt，模拟组合矩阵和数字组合矩阵的乘积WRFWBB接近无约束全数字组合矩阵Wopt，因此所实现频谱效率会接近无约束全数字预编码。

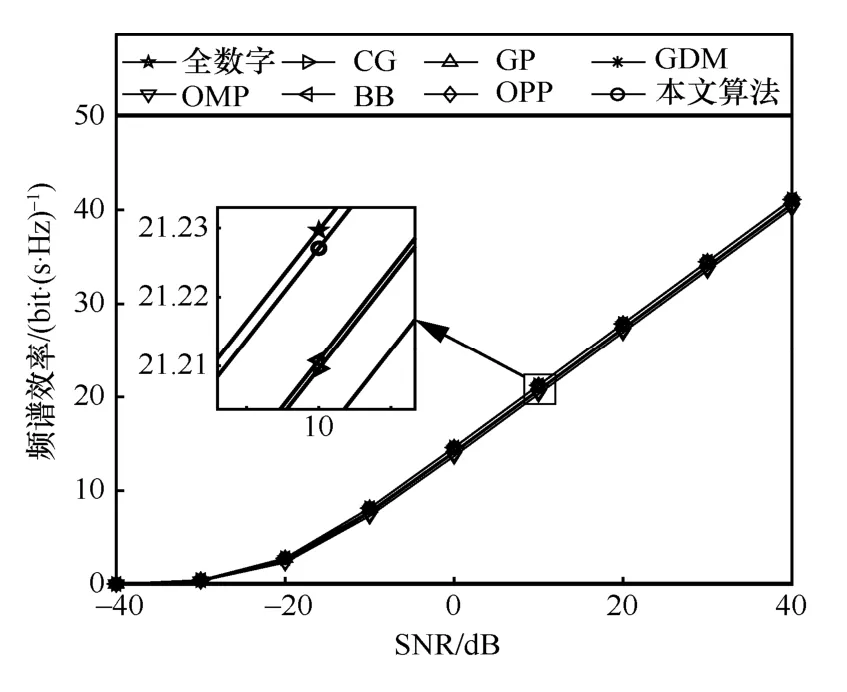
图4 NRF=4时不同算法的性能对比

图5 为不同算法可实现的频谱效率随NRF的变化情况。随着NRF的增加，本文算法、OMP、CG-AltMin、BB-AltMin、GP-AltMin 和GDM 可实现的频谱效率均增加。在给定NRF的条件下，本文算法可实现的频谱效率高于其他算法，且在NRF=4时接近无约束全数字预编码的性能。文献[33]证明，在混合预编码架构下，NRF≥2NS是实现无约束全数字预编码性能的充分条件，图5 的仿真结果也证实了这一结论。尽管OPP 相比上述算法具有较低的复杂度，但可实现的频谱效率随着NRF的增加几乎不发生变化。这是由于OPP 假设FBB满足比例酉性质，但这一假设仅在NRF=NS时成立。因此，当NRF>NS时，OPP 所实现的频谱效率在一定程度上会有所降低。

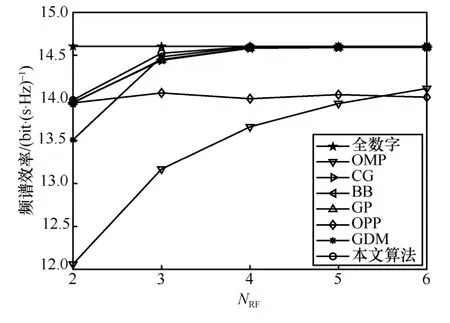
图5 不同算法可实现的频谱效率随NRF的变化情况

为了比较不同算法的复杂度，表3 列出了本文算法、CG-AltMin、BB-AltMin、GP-AltMin 和GDM在不同NRF时的平均迭代次数。将表3 的数据代入表2 的公式中，得到不同算法的计算开销随NRF的变化曲线，如图6 所示。从图6 中可以看出，本文算法的复杂度明显低于CG-AltMin、BB-AltMin、GP-AltMin 和GDM，且在NRF>3时随着NRF的增加而降低。因为表3 的数据显示，当NRF>3时，随着NRF的增加，本文算法的迭代次数Niter不断降低，将Niter代入表2 的公式中，Niter降低的幅度大于复杂度仅在NRF作用下增加的幅度，Niter和NRF的联合作用造成复杂度的降低。而参与对比的交替最小算法和GDM 算法的迭代次数尽管也随着NRF的增大而减小，但减小的程度远不如本文算法，因此没有出现复杂度随NRF增加而降低的情况。

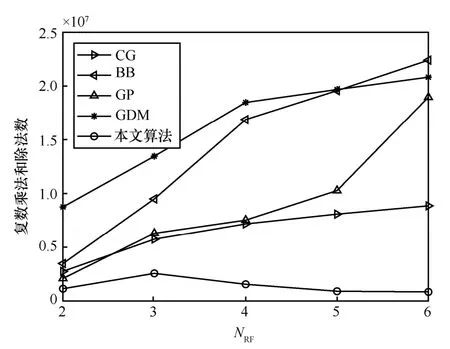
图6 不同算法的计算开销随NRF的变化曲线

表3 不同算法的平均迭代次数

最后，评估多用户场景下不同算法的性能。设配置64 根天线的基站同时和U个用户进行通信，每个用户均具有16 根天线。每个用户与基站间毫米波信道实例的产生方式与相应参数的设置与单用户场景一致。以下在随机产生1 000 个信道实例的条件下，将本文算法与 ZF[18]、MMSE[19]、CG-AltMin[13]和GDM[22]进行对比分析。

图7 为U=4时不同算法的和速率与SNR 的关系。根据式(27)，随着SNR 的增加，所有算法可实现的和速率均增加。从图7 中可看出，本文算法实现的和速率高于其他算法，这是因为本文算法设计的混合预编码矩阵最接近理想情况下的ZF 全数字预编码矩阵。

图7 U=4时不同算法的和速率与SNR 的关系

图8 为SNR=0 时不同算法的和速率与U的关系。随着U的增加，所有算法实现的和速率均增加，但U的增加会造成每个用户所受干扰的增大，因此和速率增长的趋势会变缓。在给定U的前提下，本文算法实现的和速率与GDM 基本相同，且均高于ZF 和MMSE。与CG-AltMin 相比，当U≤ 4时，本文算法实现的和速率与之相同；当U>4时，本文算法实现的和速率更高；且随着U的增加，本文算法和CG-AltMin 所实现和速率的差值不断增大。

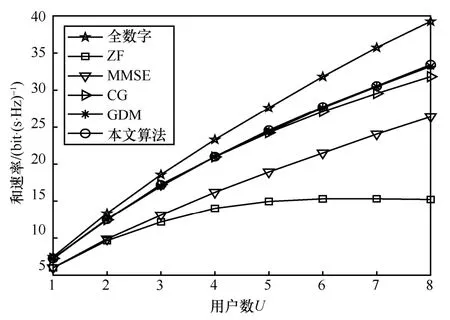
图8 SNR=0 时不同算法的和速率与U 的关系

综上所述，在单用户场景和多用户场景下，本文算法可实现的频谱效率均高于现有的算法，接近全数字预编码的性能。而在算法复杂度方面，与基于交替最小的次优算法和基于GDM 的在线学习方案相比，本文算法的复杂度明显降低。

5 结束语

本文针对毫米波大规模MIMO 系统，分别提出了适用于单用户场景和多用户场景的低复杂度混合预编码方法。首先针对单用户场景，提出了一种等效的单隐藏层神经网络架构，将混合预编码的设计问题等效为该网络架构下的权值训练过程。然后以最小化损失函数为目标，提出了基于AG-BP 算法的混合预编码机制。最后将所提算法扩展至多用户场景。仿真结果表明，所提算法可实现的频谱效率高于现有的算法，接近全数字预编码的性能，且复杂度低于基于交替最小的次优算法和基于动量梯度下降的在线学习方案。