针对工业控制拓扑的确定性局部多点故障检测方法

梁若舟，赵曦滨，万海

（清华大学软件学院，北京 100084）

1 引言

时间敏感网络（TSN，time-sensitive networking）是一种确定性传输网络。它确保了可靠、确定和实时的网络数据传输，满足了工业控制应用对实时性、确定性的需求。TSN 根据预先计算的调度表传输实时数据。调度表是根据网络拓扑结构和应用数据传输要求获得的。当网络发生故障（如链路故障）时，网络拓扑会发生改变，从而导致调度表失效，引起实时数据传输服务的降级。当网络发生故障时，为了重新计算调度表，TSN 需要对发生故障的链路或节点进行定位，以获得最新的网络拓扑。调度表的重新配置将中断实时数据传输。因此，需要在确定的时间内尽快获得最新的网络拓扑。

工业场景下的故障检测是一类非常重要的问题，其中包括过程层的异常检测[1]和网络层的故障检测。过程层的异常检测主要关注工业生产过程中的数据是否正常。Wuest 等[2]使用有监督机器学习的方法检测异常。由于工业过程数据具有高维、复杂和非线性等性质，Huang 等[3]提出使用核字典学习的方法解决这一问题。针对真实工业场景中标签较少的问题，Huang 等[4]使用半监督字典学习方法为过程监控提供有效模型。网络层的故障检测主要关注网络中的链路故障的发现和定位。对于网络故障检测目前已有很多研究。主流的方法可分为两类。第一类采用局部状态感知技术。网络设备向其邻居发送链路层发现协议数据（LLDPDU,link layer discovery protocol data unit）以获取其他设备的状态，然后将收集到的状态信息发送到网络的控制器节点。第二类采用检测流进行故障检测。一组检测包从端节点发送，通过预定义的路径覆盖网络中的每个链路，最后到达控制器节点。控制器节点再根据每个检测包的到达状态（到达或丢失）来推断每个链路的状态。第二类方法又可以细分为以下3 种。1) 基于概率的检测方法。通过发送多轮检测包来计算每条检测路径的丢包率，进而推断每条链路的拥塞概率[5-7]，文献[8]采用基于概率的贝叶斯网络检测方法来定位故障链路。2) 基于布尔观测模型的方法[9-13]，称为布尔网络测绘。布尔网络测绘模型如图1 所示，针对图1(a)的网络拓扑，生成了4 条检测流p1～p4。检测流对应的检测矩阵如图1(b)所示。矩阵的每一行代表一条检测流，行中元素为1 代表该条流覆盖对应边，为0 则代表该条流未覆盖对应边。例如，p1覆盖边A 和B，未覆盖C、D 和E。对应行则为(1,1,0,0,0)。检测矩阵的列代表对应边的故障编码。例如，边B 的故障编码为(1,1,0,0)，表示若边B 发生故障，则通过路径p1和p2的包会丢失（列元素为1 表示包丢失），通过路径p3和p4的包会顺利到达（列元素为0 表示包未丢失）。3) 针对特定拓扑结构的方法。例如，针对环形拓扑的多点故障检测方法[14]。

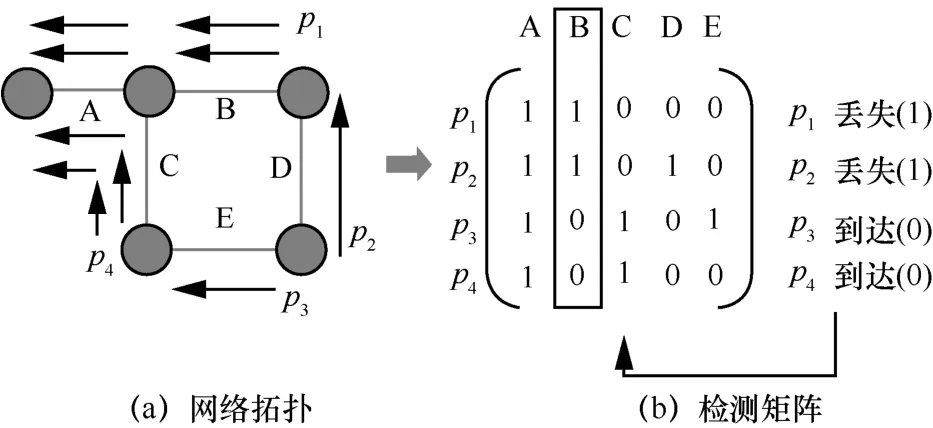
图1 布尔网络测绘模型

Duffield[15]提出的方法是检测网络故障的经典方法。它通过检测不同端到端路径的状态来推断单个链路是拥塞还是失败。文献[16]提出了一种应用于一般网络拓扑中布尔网络测绘问题的经典方法，主要分为两类：非自适应检测和自适应检测。非自适应检测[17-19]在链路故障检测过程中并行地发送所有数据包。自适应检测[10,20-22]根据已经获得的检测数据包的结果依次建立检测路径。

如何优化检测路径集也是研究热点。一些研究的目的是寻找最小检测路径集。这是一个NP-hard问题。Zeng 等[23]提出了一种网络故障自动检测系统ATPG（automatic test packet generation），通过读取路由配置和拓扑结构来生成一组最小的数据包。但由于其迭代检测策略，无法实现时间确定性检测。Bai 等[10]提出了一种利用二元观测模型进行网络监测的两阶段方法，但它只适用于单点检测。Chan等[19]提出了一种针对不同拓扑结构的非自适应组测试，并行发送最小数量的预先确定的数据包。但是该方案对拓扑的连通性有严格要求，例如，为了识别s个故障，网络拓扑的边连通度需大于或等于2(s+1)。

此外，K点可检测（K-identifiable）性质也是一个研究热点。文献[17]讨论了识别最多d个缺陷项所需的最少m条路径数的基本界问题，介绍了4 种不同场景的随机路径构造。文献[13]考虑给定m条检测路径、网络拓扑、路由方案和路径长度约束的最大可识别项目数的上界。这些文献旨在证明K-identifiable 性质，但并没有给出一种实用、有效的检测路径集的构造方法。

布尔网络测绘通过求解布尔代数中的一组线性方程组，通过端到端测量推断链路拥塞状态。一些研究集中在如何高效、准确地求解布尔代数中的模型。Chen 等[5]开发了一个学习估计方案来推断网络中的拥塞链路。文献[6]考虑了利用链路时延变化的多路径路由方案，提出了一种贪婪算法求解拥塞路径，同时兼容时延方差。类似地，文献[7]提出了一个扩展的状态空间模型，通过自上而下的贪婪算法来识别拥塞链路。然而，上述算法是对拥塞链路的概率估计，并不能确定性地识别链路故障。

在工业控制拓扑的应用场景中，一种理想的链路故障检测方法应具有以下性质。

1) 确定性检测。此处的确定性有两层含义：①拓扑发现所用的时间是有界的；②方法检测到的链路状态是确定性的，而不是概率性的。

2) 网络负载优化。检测方法应使用尽可能少的检测包，以减少带宽消耗。

3) 多点故障检测。检测方法应尽可能多地发现故障。

4) 适用于工业控制拓扑。工业控制拓扑具有局部连通度高、整体连通度低的特点。例如，在图2所示的工业控制拓扑中，在路径S0—S1—S8—S12—S16—S20—S24中只能实现单点故障检测，但在局部如Car1中可以实现多点故障检测。

图2 一种工业控制拓扑

目前的方法并不能完全满足工业控制拓扑链路故障检测的上述4 个性质。具体而言，它们具有以下不足之处。

1) 检测时间不确定。基于概率的检测方法[5-7]预测链路失效或拥塞的概率，不能满足确定性检测的要求。基于布尔网络测绘的方法[9-13]需要多轮迭代检测，存在检测时间不确定的问题。

2) 未对网络负载优化。当前方法未对生成的检测包数量进行优化，影响性能。

3) 无法应对多点故障检测场景。Bai 等[10]提出的基于二元观测模型进行网络监测的两阶段方法只能应用于单点故障检测。

4) 无法适应工业控制拓扑特点。当前方法未针对工业控制拓扑整体连通度低、局部连通度高的特点进行优化，降低了对于局部高连通度部分的检测能力。

针对以上不足之处，本文提出了一种针对工业控制拓扑的确定性局部多点故障检测方法。该方法的基本思路如下。

首先，根据当前网络拓扑结构，识别网络中连通度较低的主干部分和连通度较高的簇，对主干部分使用单点故障检测方法生成检测流，对簇使用多点故障检测方法生成检测流。然后利用检测流优化算法减少检测流的数量。每个检测流从某个节点开始，经过指定的路由，最后到达TSN 控制器。

其次，为每个检测流分配一个传输周期和最坏时延，并在此基础上生成检测流的TSN 调度表。当网络运行时，每个检测包从起始节点按照预定的时间周期与检测流一起周期性地发送，并到达TSN 控制器。当故障发生时，一些检测包将无法到达TSN控制器。TSN 控制器定期收集每个检测包的到达或故障状态信息，并使用拓扑发现算法获得链路状态和网络拓扑。

此外，为了保证整个故障检测过程的时间确定性，检测流需要在确定的时间范围内到达控制器。本文将检测流实现为TSN 数据流，从而实现了检测流传输的时间确定性。IEEE 802.1Qav 标准中阐述了队列及转发协议能够确保传输时延控制在一定的范围内；IEEE 802.1Qbv 标准中使用了时间感知整形器，保障业务流消息的传输时延是确定的；IEEE 802.1Qch 标准中引入了周期性排队与转发机制。上述3 个标准可以保证检测流在确定的时间内到达控制器节点。IEEE 802.1 Qca 标准定义的路径控制和保留，以及IEEE 802.1CB 标准定义的帧复制和消除可以控制每个检测流的路由。

本文贡献总结如下。

1) 基于工业控制拓扑的场景，本文提出了一种基于布尔网络测绘的确定性局部多点故障检测方法。本文提出的检测框架可以针对工业拓扑主干连通度低、局部连通度高的特点，生成近似最优的检测路径集，实现局部多点故障检测。利用TSN 的确定性传输机制，该检测过程时间上界是确定的。

2) 本文进行了全面的实验来评估所提检测方法。与已有的故障检测方法相比，所提方法能够在确定的时间内准确地识别出多个故障链路，生成的最小检测路径集优于随机游走法和 NACGT（non-adaptive combinatorial group testing）[18]法。

2 系统模型与问题定义

2.1 网络模型

网络拓扑被定义为一个无向图G(V,L)。所有交换机和端节点的集合由顶点表示。所有物理链路的集合由边表示。

所有通过物理链路连接的顶点都可以直接通信，并且物理链路是全双工的。链路连接节点vi∈V和节点vj∈V。因此，物理链路也可以表示为本文假设交换机和节点不会发生故障，仅物理链路可能发生故障。链路有2 种状态：故障链路和正常链路。所有故障链路的集合称为故障链路集，表示为F⊆L。

检测路径由一系列相邻的链路组成，并且不包含环，定义为p。检测路径表示为路径所经过的物理链路集。如果链路lj被检测路径pi经过，则lj∈pi。如果∃lk∈pi,lk∉pj，则pi≠pj。

因此，本文的目标是通过一组检测路径P={pi|i=0,1,2,…,z} 来识别故障链路集F，其中z表示检测路径的数目。

2.2 布尔测绘图和检测矩阵

用布尔形式来表示物理链路的状态，xi=0 表示链路正常，xi=1 表示链路故障。因此，物理链路li的状态可定义为

用一个布尔状态向量来表示整个网络的链路状态，链路状态向量为x=(x1,x2,…,xm) ∈{0,1}m。

用一个布尔状态向量来表示所有检测流的状态，检测路径的状态向量为y=(y1,y2,…,yz)∈{0,1}z。

相应地，可以得到链路状态向量和检测路径状态向量之间的关系为

其中，∨是逻辑或运算。

布尔检测矩阵可以根据一系列检测路径P有效地推断链路的状态x（故障或正常）。布尔检测矩阵R是一个z×m的矩阵。如果链路lj被检测路径pi遍历，则Ri,j=0。布尔检测矩阵R的第i行表示一个检测路径pi，而第j列表示链路lj的二维编码向量。式(3)转换成矩阵形式为

2.3 K-identifiable 性质

本节讨论一个检测矩阵R可以识别最多K个故障链路的充要条件。

假设网络中有K个故障链路。不失一般性地，给定链路状态向量x，其中，则检测路径状态向量y可以表示为

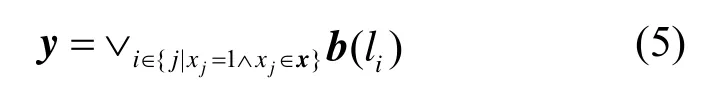
也就是说，对所有在故障链路集合中的链路li的二维编码向量b(li)（li∈F）执行逻辑或运算。

布尔检测矩阵R满足K-identifiable 性质，它的含义是：如果网络中最多有K个故障链路，则由式(4)计算的所有y的结果都是不同的。这个结论可以描述为定理1[11]。

定理1给定一组检测路径P和一个链路li∈L，如果对于任何 2 个故障集F1和F2，F1∩{lj}≠F2∩{lj}，且Fi≤K(i∈{1,2})，满足

则称li相对于P满足K-identifiable 性质。

扩展定理1 来研究单点故障识别问题，考虑K=1，则得到引理1。

引理1链路li相对于P满足1-identifiable 性质，当且仅当b(li) ≠0，且∀li≠lj,b(li)≠b(lj)。即其二维编码不为空，且与任何其他链路的二维编码不同。

对于一个满足K-identifiable 性质的检测矩阵，如果存在不超过K条故障链路，那么所有故障链路都可以通过z条检测路径进行准确识别和定位。

2.4 局部K 点可检测性质

在工业控制网络中，由于全局网络的边连通度较低，不满足K-identifiable 性质，但局部网络往往具有较高的边连通度。因此，更常用的情况是一个网络满足局部K点可检测（local-K-identifiable）性质。

也就是说，对所有在簇内故障链路集合中的链路li的二维编码向量执行逻辑或运算。

如果一个簇C满足local-K-identifiable 性质，它的含义为，如果簇内最多有K个故障链路，则由式(7)计算的所有ycr的结果都是不同的。通过引申定理1，该结论可以描述为引理2。

则称li在簇cr内相对于P满足local-K-identifiable性质。

2.5 问题定义

由于全局网络的边连通度较低，可能不满足K-identifiable 性质。这会使一些网络仅可以进行单点故障检测。但事实上，网络的稠密是不均匀的，局部比较密集的网络可以实现多点故障检测。可以将这些比较稠密的局部网络识别为簇，对每个簇进行多点故障识别。因此，需要设计一种有效的检测矩阵构造方法，使用尽可能少的检测路径，使每个簇满足local-K-identifiable 性质。该约束优化问题定义为

其中，C表示网络中簇的集合；表示检测簇cr的局部检测矩阵；Rc表示检测非簇链路的局部检测矩阵；表示簇cr中最多有K个故障链路的所有故障链路集合；z表示布尔检测矩阵R的总行数，z也是检测流的总数量，它等于各个分簇的检测流与非簇检测流的数量之和。

3 确定性多点故障检测机制

本节详细介绍确定性多点故障检测方法，方法流程如图3 所示。该方法分为两部分：离线检测矩阵计算和在线故障检测。

图3 确定性多点故障检测方法流程

离线检测矩阵计算的目标是构造一个检测矩阵，该矩阵在满足K-identifiable 性质的前提下，所需的检测流数尽可能少。此阶段进一步分为3 个步骤。

步骤1基于马尔可夫链（MC,Markov chain）采样算法，提出了改进的基于马尔可夫链的采样算法，以得到一组初始检测路径（用P0表示）。由初始检测路径P0所构成的检测矩阵被表示为初始检测矩阵R0。

步骤2检查R0是否满足K-identifiable 性质。如果是，则转到步骤3；如果不满足，则使用构造性算法使其满足。本文提出了一种构造性算法，称为矩阵修补算法。该算法的原理是：构造新的检测路径并将其添加到P0，直到检测矩阵满足K-identifiable 性质。通过该步骤获得的一组检测路径被表示为P1，其相应的检测矩阵被表示为R1。

步骤 3本文采用一种迭代策略，在保持K-identifiable 性质不变的情况下，安全地删除P1中的检测路径，然后用更少的路径得到满足定理1 的一组近似最优检测路Popt和近似最优检测矩阵Ropt。

在线故障检测在得到近似最优检测矩阵Ropt后，沿着从Ropt派生的路径，并行地周期性发送检测包，根据一定时间内检测包到达控制器的状态来获得路径状态向量y，并使用式(5)求解链路状态向量x。在实际的检测过程中，只需要将向量y存储为Key，而将向量x对应的故障链路集合F设置为Value，即可在线性时间内找到所有的故障链路。

因此，确定性多点故障检测机制的关键算法是改进的基于马尔可夫链的采样算法（用于获取初始检测矩阵）和矩阵修补算法（基于初始检测矩获取满足K-identifiable 性质的检测矩阵）。

3.1 改进的基于马尔可夫链的采样算法

本文提出的检测方法需要得到一个可以直接满足K-identifiable 性质的检测路径集。一个简单的思想是采样。由于不可能枚举所有合法的检测路径，因此传统的基于概率的采样方法（如高斯分布抽样）是不适用的。一种实用的方法是随机游走采样。随机游走采样的本质是一阶马尔可夫链，因此本文将其记为MC-采样（Markov chain sampling）。

MC-采样不能以高概率直接获得满足K-identifiable 性质的初始检测矩阵。因此，需要一种具有引导性的随机游走抽样方法。该方法能以较大的概率获得满足K-identifiable 性质的初始检测矩阵。

如果链路l1被大量的检测路径经过，那么l1发生故障，这些路径都将受到影响。如果检测路径之间的重叠度太大，则一条链路发生故障，将降低其他检测路径的检测能力。因此，每个链路通过的路径数应该相对平均，并且每个检测路径之间的重叠应该降低。本文提出的Weighted-MC 采样算法如图4 所示。

图4 Weighted-MC 采样算法

每个状态跳转到邻居节点、跳回父节点或停留在其自身的概率与候选邻居链路的通过检测路径数有关。如果该链路已经通过大量检测路径，则其跳转的概率将降低。设当前节点i共有t个邻居节点，对这t条边按照通过的检测路径数目降序排列，当前节点到相邻节点的概率为

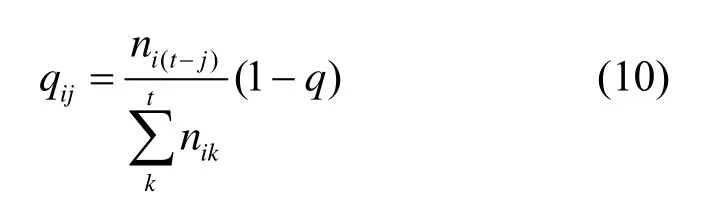
其中，qij表示节点i到节点j的转移概率，nik表示通过以i和k为节点的边路径数量，q表示节点到自身的转移概率。图4 中，当前状态si对应节点vi，其父节点是vi-1，邻居节点是vi+1和vi+2。

3.2 矩阵修补算法

当2 个链路状态向量x通过检测矩阵R0映射到同一路径状态向量y时，初始检测矩阵R0不能满足K-identifiable 性质。解决该问题的一个方法是添加新路径。本节阐述了一种矩阵修补算法，通过构造新的检测路径，使初始检测矩阵满足K-identifiable 性质。

定理2假设在(K+1)-边连通图中构造了满足K-identifiable 性质的检测矩阵R，如果存在2 个不同的链路状态向量x和x′，它们被检测矩阵R映射到相同的检测路径状态向量y，则可以构造一个新的检测路径来区分x和x′。

证明假设由x和x′表示的故障链路集是Fi和Fj，Fj≥Fi。Fi和Fj之间有3 种关系：Fi⊂Fj，Fi∩Fj=∅，Fi∩Fj≠∅,Fi⊄Fj。

1)Fi⊂Fj。由于检测矩阵最多能识别K个故障链路，因此≤K。对于任何一个故障链路l∈Fj-Fi，l至少有一条新的路径可以路由到控制器而不经过Fi中的链路。因为在消除了Fi中的所有链路之后，整个网络的边连通度仍然为1。通过引入一条新的检测路径，被x映射的检测路径状态向量变为[y,0]，而被x′映射的检测路径状态向量变为[y,1]。由此，可以区分Fi和Fj。

2)Fi∩Fj=∅和Fi∩Fj≠∅,Fi⊄Fj同理可证。

因此，本文提出矩阵修补算法，如图5 所示，枚举所有链路状态向量x，根据初始检测矩阵R0将链路状态向量映射到检测路径状态向量y，然后对具有相同映射关系的每对向量，构造新的检测路径来区分它们。构造新的检测路径的方法如下：首先寻找一条链路l，l只属于x对应的故障集Fi或者l只属于x′对应的故障集Fj，若l∈Fj，则从控制点v0开始进行广度优先搜索，找到一条从v0到l的路径p，p上所有边均不属于Fj；若l∈Fj，则从控制点v0开始进行搜索，找到一条从v0到l的路径p，p上所有边均不属于Fj。矩阵修补算法得到的检测路径p即为满足要求的新的检测路径。

图5 矩阵修补算法

4 确定性局部多点故障检测机制

并不是所有的拓扑都满足K-identifiable 性质，一些拓扑整体的边连通度不高，可能仅能满足1-identifiable 性质，但局部具有较高的边连通度，可以形成一个局部的簇，如列车通信网络。针对这种拓扑，如果仍使用确定性多点故障检测机制，则会将问题降级为单点故障检测问题，损失了整个网络故障识别的能力。本文提出的方法能够在网络中连通度较高的局部使用确定性多点故障检测，在连通度较低的主干网络实现单点故障检测，提升了网络整体的故障检测能力。

本文将这种网络抽象为图6 所示的网络拓扑。整个网络抽象为边连通度较低的树干和边连通度较高的簇。图6 中的×表示该链路发生故障。如果链路li发生故障，则无论簇内的链路状态如何，经过簇内的检测路径均会被li影响，不能到达控制器。因此，整个网络降级为单点故障检测。

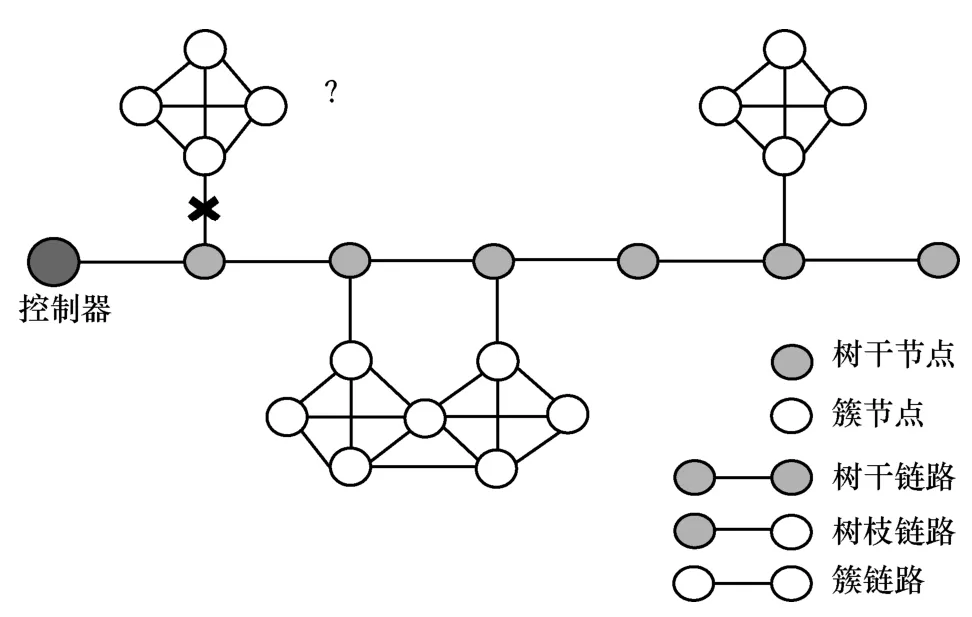
图6 连通度不均匀的网络拓扑

本文的目的是设计一种确定性局部多点故障检测机制，降低K-identifiable 性质对该拓扑的约束，从而满足树干单点检测、簇内多点检测的性质，即满足local-K-identifiable 性质。基于此，将网络中的节点分为两类，链路分为三类具体描述如下。

1) 树干节点vtree，指一系列边连通度较低的节点。树干节点可以理解为一个网络的交通枢纽，会以较高的流量被检测路径所经过。

2) 簇节点vnon-tree，指一系列边连通度较高的节点。本文将一个网络中的非树干节点都看作是簇节点。

3) 树干链路ltree，树干节点和树干节点相连的链路称为树干链路。

4) 树枝链路lbranch，树干节点和簇节点相连的链路称为树枝链路。

5) 簇链路lcluster，簇节点和簇节点相连的链路称为簇链路。

与全局性确定性多点故障检测机制相同，该机制主要分为两个阶段：离线检测矩阵计算阶段和在线故障检测阶段。

离线检测矩阵计算的目标是构造一个检测矩阵，使在同一个簇内的链路满足local-K-identifiable性质，不在任何簇内的节点满足单点故障检测性质，同时，其所需的检测流数目尽可能少。此阶段进一步分为以下步骤。

步骤1对网络拓扑进行预处理，通过基于流量的树干节点识别算法识别出所有的树干节点，然后对剩余的节点进行分簇，形成r个簇C={c0,c1,…,cr}，使具有较高连通度的节点们被分到一个簇内。

步骤2对包含树干链路、树枝链路的簇外链路进行检测矩阵的生成。将生成的检测矩阵称为簇外检测矩阵。该检测能满足对簇外链路的单点故障识别（K=1）。

步骤3对簇外检测矩阵中的每一条连接簇的检测路径，利用针对簇的随机游走采样算法，对簇进行延伸检测，生成若干新的检测路径，称为初始簇检测路径（用表示）。由初始簇检测路径所构成的检测矩阵被表示为初始簇检测矩阵。

步骤4计算该簇的边连通度为K+1，检测是否满足local-K-identifiable 性质。如果满足，则跳转至步骤3。如果不满足，则使用针对簇的矩阵修补算法对该簇进行修补，通过构造新的检测路径并将其添加到直至该簇满足local-K-identifiable 性质。将通过该步骤获得的检测路径表示为，相应的检测矩阵表示为。

步骤 5采用迭代策略，在保持该簇local-K-identifiable 性质不变的前提下，安全地删除中的检测路径，获得一组路径数量更少的近似最优簇检测路径和近似最优簇检测矩阵。

步骤6重复步骤3～步骤5 直至对所有的簇完成构造，通过合并所有的检测路径，得到最后的检测矩阵Ropt。

4.1 网络预处理

本节对网络拓扑进行预处理，区分所有的树干节点、簇节点、树干链路、树枝链路和簇链路。然后针对簇链路和非簇链路分别生成检测路径。该过程分为两步：首先识别出所有的树干节点，然后对剩余的节点进行分簇。

分簇可以利用图论的理论知识，将整张图进行分割。例如，统计出节点与节点之间的边连通度，用二维矩阵表示，再利用相似度原理进行分割。但节点与节点的边连通度计算本身具有较高复杂度，相似度分割也会使问题变得复杂。需要找到一个更加简便高效的树干识别和分簇算法。因此提出基于流量的树干节点识别算法和分簇算法。

4.1.1基于流量的树干节点识别算法

基于流量的树干节点识别算法如图7 所示。簇内的节点如果想与控制器通信，必须经过树干节点。因此，树干节点具有较高的流量。一个简便可行的方法是基于概率的原理，以任意节点为起始节点，利用广度优先搜索（BFS,breadth first search）算法寻找其到控制器节点的一条检测路径，并将路径上经过的节点流量均加1。生成W条检测路径后，将所有节点按照被经过的次数降序排列，选取前|V|δ个节点作为树干节点，其中，|V|表示拓扑中节点个数；δ表示选出节点的比例，是取值范围为(0,1)的超参数。

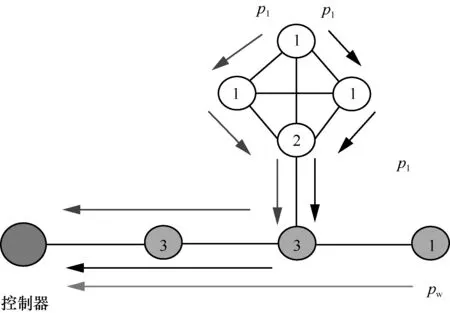
图7 基于流量的树干节点识别算法

4.1.2分簇算法

本节利用分簇算法对剩下的节点进行分簇，识别出所有的簇。分簇算法的思想很简单，将所有连通的簇节点划分为一个簇。因此，只要对所有的非簇节点遍历，利用BFS 算法进行划分即可。

所有的非树干节点被分簇，标记每个簇的ID后，接下来对链路进行分类。链路的分类很简单，只需要遍历所有链路，确定该链路所连接的2 个节点的类型即可。连接树干节点和树干节点的链路被划分为树干链路，链接树干节点和簇节点的链路被划分为树枝链路，链接簇节点和簇节点的链路划分为簇链路。

4.2 离线检测矩阵的计算

对所有的链路进行分类后，即可以生成检测矩阵。检测矩阵的生成步骤与确定性多点故障检测机制相似，不同的是，需要对不同的链路分别进行检测矩阵的生成。首先，利用簇外检测矩阵生成算法对所有的树干链路和树枝链路进行检测矩阵的构造，使其满足单点故障检测性质。然后，利用针对簇的随机游走采样算法，针对簇的矩阵修补算法和针对簇的矩阵优化算法对簇链路进行检测矩阵的生成，使每个簇满足local-K-identifiable。

4.2.1初始检测矩阵生成

树干链路和树枝链路会形成类似树的结构。则该问题转化为用最少的检测路径对一棵树进行单点故障检测。簇外检测矩阵生成算法拓扑转化如图8 所示。对每个树枝链路进行检测，需要生成一条以树干链路为始的检测流；同时，存在一些树干链路无法被区分。因此，该问题的实质是以每个叶子节点和单个子节点为出发节点，生成检测路径。在图8 中，虚线圈出的节点为需要生成检测路径的出发节点。

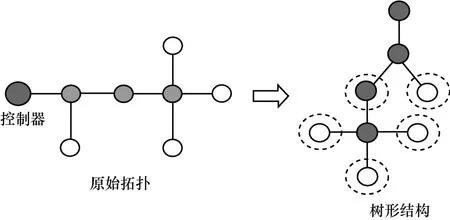
图8 簇外检测矩阵生成算法拓扑转化示意

基于上一步生成的簇外检测矩阵，可以再对每一个簇的簇链路进行检测路径的构造。构造的方式与确定性多点故障检测机制相同，构造马尔可夫链，在簇内采用随机游走的策略，对检测路径进行采样，使其以较大的概率满足local-K-identifiable性质。

4.2.2簇检测矩阵修补和优化

4.3 在线故障检测

在生成了近似最优检测矩阵Ropt后，将检测矩阵转化为检测流，在网络中周期性地由终端节点发送至控制器节点，控制器节点通过收集一定时间内检测报文的到达情况生成路径状态向量y。接着可以根据y，反推出链路状态向量x，进而得出故障链路集F。在确定性多点故障检测机制中，根据式(4)，任何检测路径状态向量y对应于检测矩阵Ropt中任意（k k≤K）个二维编码b(li)的“或”操作。但是，在确定性局部多点故障检测中，由于Ropt是由簇外检测矩阵（单点故障检测）和各个簇检测矩阵（多点故障检测）组成的，部分路径状态向量y是不存在的，因此不能直接反推出x。

本节提出离线含簇故障定位算法，枚举所有可能的链路状态向量x，通过Ropt映射得到所有合法的路径状态向量y，并将y存储为Key，链路状态向量x所对应的故障链路集F存储为Value。

步骤1簇外矩阵满足单点故障检测性质。因此遍历所有的树干链路和树枝链路，用表示，假设该链路故障，则所有包含该链路的检测路径均失败，将检测路径对应的位数表示为1，从而得到其对应的路径状态向量y0。同时，将该链路放入故障链路集F中。该链路发生故障后，其相关联的簇内链路状态无法进行检测，因此将与之相关联的簇内链路均视为故障链路，放入故障链路集合F中，如图9 中的虚线圈内链路所示。若所有的树干链路和树枝链路均未发生故障，则路径状态向量y0表示为全零向量，故障链路集表示为空。

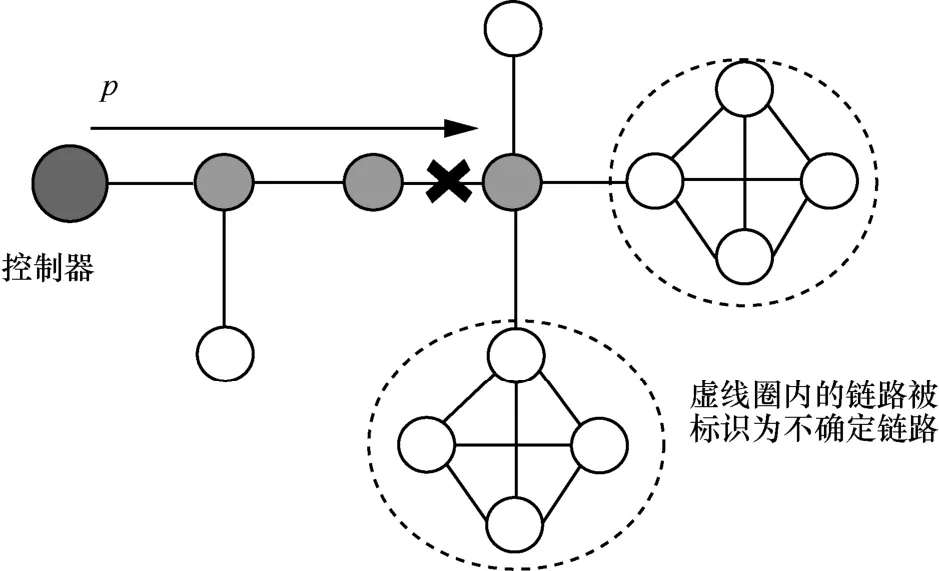
图9 离线含簇故障定位算法步骤1

步骤2各个簇满足local-K-identifiable 性质。因此，需要检查各个簇是否发生多点故障，如图10所示。对每个簇，假设该簇内的任意（k k≤K）个链路发生故障，将这些链路加入故障链路集F中，并将包含该k个链路的检测路径均视为失败，更新路径状态向量y0中这些检测路径相应的位数为1，得到新的路径状态向量yupdate和Fupdate。遍历所有簇（不包括步骤1 中的簇）后，即可得到最终的路径状态向量y和F。

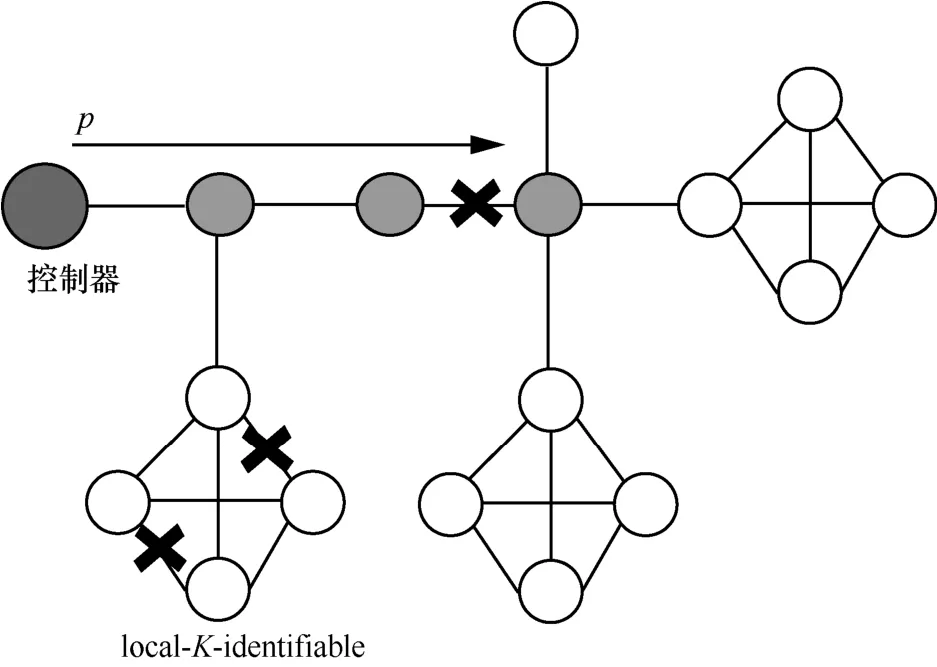
图10 离线含簇故障定位算法步骤2

5 系统验证

本文进行了一系列实验来验证本文方法的以下优势：1) 在不同的工业控制拓扑中，与基线方法相比，本文方法生成的检测路径数量更少；2) 随着链路数量的增加（即网络规模增大），本文方法能产生合理数量的检测路径。

5.1 仿真实验

本文仿真实验使用Java 语言实现，并将网络抽象为节点、链接等对象；使用二元连通矩阵来表示拓扑结构，作为整个网络的输入，同时控制采样数、采样方法等变量，对最小检测路径数z和最大可识别故障K指标进行了评价。

5.2 基线方法

本文采用以下算法作为基线方法。

1) 随机游走。文献[17]介绍了一种随机游走构造方法来构造检测矩阵。其目标是设计一个最小行数的m×n布尔检测矩阵。从本质上说，这是MC-采样的概念。将这种方法应用到本文的实验场景中，只需要保持采样直到满足K-identifiable 或local-K-identifiable。

2) NACGT[18]。NACGT 适用于2K+1 边连通度的网络拓扑来检测至多K个故障。其思想是具有2K+1 边连通性的网络至少有K+1 个边不相交的生成树。因此，至少有一个生成树不包含故障链路。使用树作为“跳板”来访问树外的链路。假设生成树完好无损，当且仅当树外链路为故障链路时时，该检测包才会失败。

5.3 几种典型的工业控制拓扑

为了验证该方法在工业控制领域的通用性和正确性，本文在2 种不同的应用场景下进行了仿真。这些应用场景包括一种典型的工业网络——列车通信网络（如图2 所示）、星形拓扑网络（如图11所示）和规模较大的工业控制网络。设置采样数为5m，m表示网络拓扑中链路的数量，转移迭代步长为50。列车通信网络由于拓扑关系，最多只能实现全局1-identifiable，而NACGT 方法不适用于这3 种拓扑。

图11 星形拓扑网络

列车通信网络的实验结果如表1 所示。随机游走方法对应的最大K值为1，表示该方法只能适用于检测故障数量为1 的情况，而本文方法最大K值为2，表示本文方法可检测故障数量为1 或者2 的情况，所以相较于随机游走算法，本文方法能够适用于更多检测场景，有更强的检测能力。而本文方法最少检测路径多于随机游走，是由于本文方法检测了更多情况。实验结果证明了本文方法能够实现多点故障检测，同时也证明了本文方法针对整体连通度低但局部连通度高的情况，有更强的检测能力。

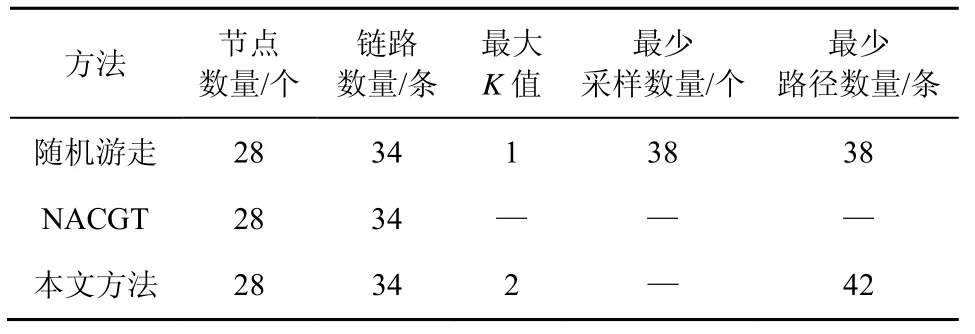
表1 列车通信网络的实验结果

针对星形拓扑网络的实验结果如表2 所示。随机游走于本文方法对应的最大K值都为2，但是本文方法生成的最少路径数量小于随机游走。实验结果证明了本文方法生成的检测流具有更高的效率，能够更好地满足网络负载优化的要求。

表2 星形拓扑网络的实验结果

工业控制网络的实验结果如表3 所示。随机游走于本文方法对应的最大K值都为4，但是本文方法生成的最少路径数量小于随机游走。实验结果证明了本文方法具有更高的效率，能够更好地满足网络负载优化的要求。

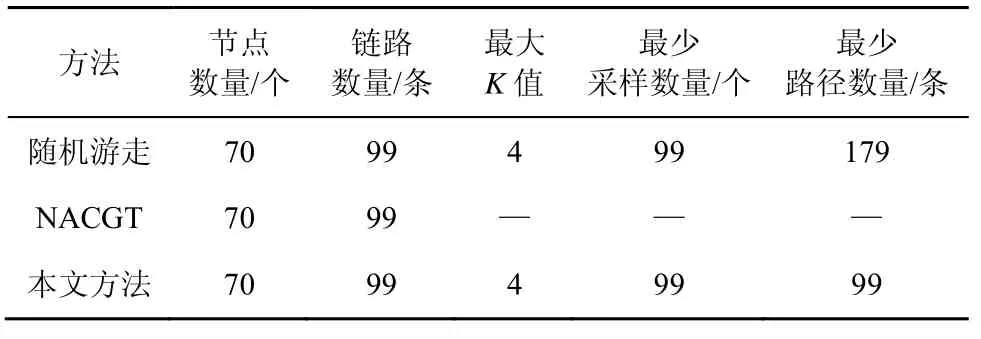
表3 工业控制网络的实验结果

5.4 网络规模性能对比

本节研究最少检测路径数随链路数的增加而变化的趋势。本文使用具有不同车厢数的列车通信网络，设置采样数为5m，m表示网络拓扑中链路的数量，传输迭代步长为50，车厢数为7～11（对应的链路数为35～55 条），每节车厢的连通度设置为2，实验结果如图12 所示。随着链路数的增加，优化的近似最优矩阵的最小数目，即最少测量路径数线性增加。

图12 最少检测路径数与链路数关系（连通度为2）

设置车厢数为7～11（对应的链路数为56～88 条），每节车厢的连通度设置为3，实验结果如图13 所示。随着链路数的增加，优化的近似最优矩阵的最小数目仍线性增加。

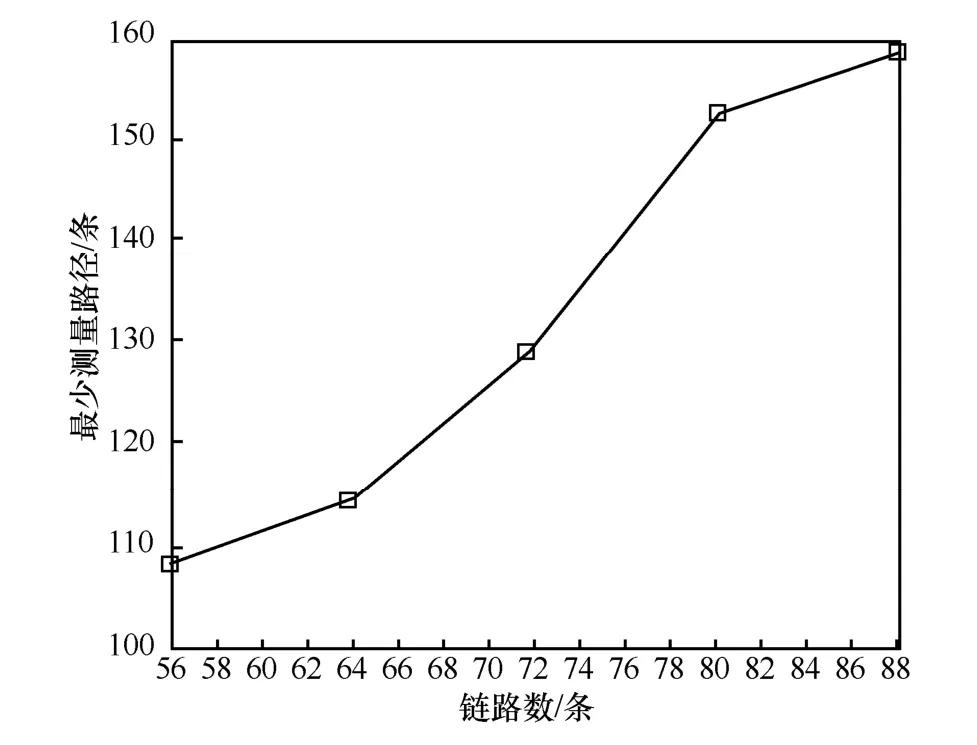
图13 最少检测路径数与链路数关系（连通度为3）

6 结束语

故障检测一直是研究的热点问题。它对于可靠和实时的数据传输尤其重要。基于TSN 提出了故障检测方法的要求：确定性检测、网络负载优化、多点故障检测机制和适用工业控制网络。然而，现有的故障检测方法都不能很好地满足上述要求。本文设计了一个多点故障确定性检测方法来寻找近似最优的最小检测路径。本文方法能够弱化拓扑约束，将单点故障检测功能升级为局部多点故障检测。算法分为离线检测矩阵计算阶段和在线故障检测阶段。离线检测矩阵计算阶段，预先生成检测路径集；在线故障检测阶段，控制器采集并检测检测包的到达状态，并基于布尔网络测绘模型进行故障检测和定位。最后通过仿真实验验证了本文方法的优越性。