纳米改性再生骨料混凝土单轴受压疲劳性能

罗素蓉，承少坤，肖建庄，游 帆,4

(1. 福州大学土木工程学院，福州 350116；2. 福建省建筑设计研究院有限公司，福州 350001；3. 同济大学土木工程学院，上海 200092；4. 福建江夏学院工程学院，福州 350108)

随着再生骨料混凝土静力力学性能和耐久性能研究的广泛进行[1-6]，近年来，再生骨料混凝土的疲劳性能研究也在逐步开展[7-8]。Thomas 等[7]研究了不同再生粗骨料取代率和水灰比的普通混凝土和再生骨料混凝土的受压疲劳性能，在相同水灰比和强度条件下，再生骨料混凝土的模量损失较大，且模量损失与疲劳寿命成反比。而肖建庄等[8]开展的再生骨料混凝土轴压疲劳性能试验表明，再生骨料混凝土的疲劳寿命比普通混凝土高；这和再生骨料混凝土配合比中的水泥用量比普通混凝土高有关。由于再生骨料来源和废混凝土工程服役情况的复杂性，导致再生骨料混凝土的性能比普通混凝土表现出更明显的离散性[9]，这种离散性在重复荷载作用下更加明显。而目前再生骨料混凝土受压疲劳性能的相关研究中，试验样本数量少，未能建立高可信度的再生骨料混凝土疲劳寿命概率方程，限制了其在工程上的应用。与此同时，再生骨料表面老砂浆的存在，增加了混凝土内部界面过渡区的种类和数量[10]，引入了更多的初始缺陷。

Saito[11]、鞠扬等[12]通过对混凝土疲劳机理探究发现，水泥石内部以及界面过渡区处的微裂纹、微孔隙是疲劳损伤开始发展的部位，疲劳对初始缺陷较为敏感，而纳米二氧化硅的火山灰活性、填充效应和晶核效应，均能有效改善混凝土的孔隙结构[13]，改善混凝土品质，徐晶和王先志[14]从宏观和微观角度对混凝土早龄期界面过渡区的性质进行研究，发现纳米二氧化硅的掺入使混凝土的宏观弹性模量得以提高，界面过渡区的致密性也明显增强。而目前纳米二氧化硅改性的再生骨料混凝土轴压疲劳性能的研究却鲜有报道，故本文采用纳米二氧化硅改性的再生骨料混凝土进行轴压疲劳试验，探究其对再生骨料混凝土轴压疲劳性能的影响。

1 试验概况

1.1 试验原材料及配合比

采用P·O42.5 普通硅酸盐水泥，密度为3150 kg/m3，比表面积为352 m2/kg；粉煤灰为Ⅱ级粉煤灰，密度为2300 kg/m3，比表面积为386 m2/kg；天然粗骨料为5 mm～20 mm 粒径的碎石，再生骨料为粒径5 mm～20 mm 的Ⅱ类再生骨料，砂浆附着率为30%；粗骨料的基本性能见表1。天然细骨料为天然河砂，细度模数为2.13，表观密度为2705 kg/m3；纳米SiO2为YD-12 型纳米SiO2分散液，指标见表2。

表1 粗骨料性质Table 1 Properties of coarse aggregate

表2 纳米SiO2 分散液性质Table 2 Properties of Nano-SiO2 dispersion

普通混凝土配合比设计目标为C40，以普通混凝土为基准设计其余三组配合比，再生骨料混凝土中的再生骨料等质量取代天然骨料；基于课题组的前期相关研究结果[15]，纳米SiO2的质量掺量(占胶凝材料和纳米SiO2的质量总和的比值)采用最优掺量，为1%；各组配合比的砂率为0.42。混凝土配合比、抗压强度及弹性模量值见表3。

表3 混凝土配合比及基本力学性能Table 3 Mix proportion and basic mechanical properties of concrete

1.2 疲劳试验

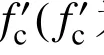
图1 1000 kN 疲劳测试系统Fig. 1 1000 kN fatigue test system

1.3 纳米压痕试验

纳米压痕技术能够测试水泥基材料中不同微观物相的力学性能、形态特征等，目前已成为先进的定量表征水泥基材料微观力学性能的测试手段[16]。试验采用Hysitron Ti Premer 纳米压痕测试系统，试样经过打磨抛光处理后，测量了改性前后再生骨料混凝土三种界面过渡区的压痕模量。将骨料-新砂浆界面过渡区称为ITZ1，骨料-老砂浆界面过渡区称为ITZ2，老砂浆-新砂浆界面过渡区称为ITZ3。纳米压痕试验采用矩阵打点的方式，选用的矩阵大小必须满足包含整个界面过渡区，在三类界面过渡区中，ITZ1和ITZ2的界面过渡区选取一样的压痕矩阵，均为100 μm×100 μm 的正方形矩阵，每两个压痕点之间的间距为10 μm，即压痕为11×11 的点阵，如图2(a)所示。新砂浆和老砂浆的界面过渡区由于宽度较大，而且不容易区分定位，所以为了确保压痕区域包含整个界面过渡区，选取150 μm×100 μm 的长方形区域，每两个压痕点之间的间距也为10 μm，即为16×11的压痕点阵，如图2(b)所示。

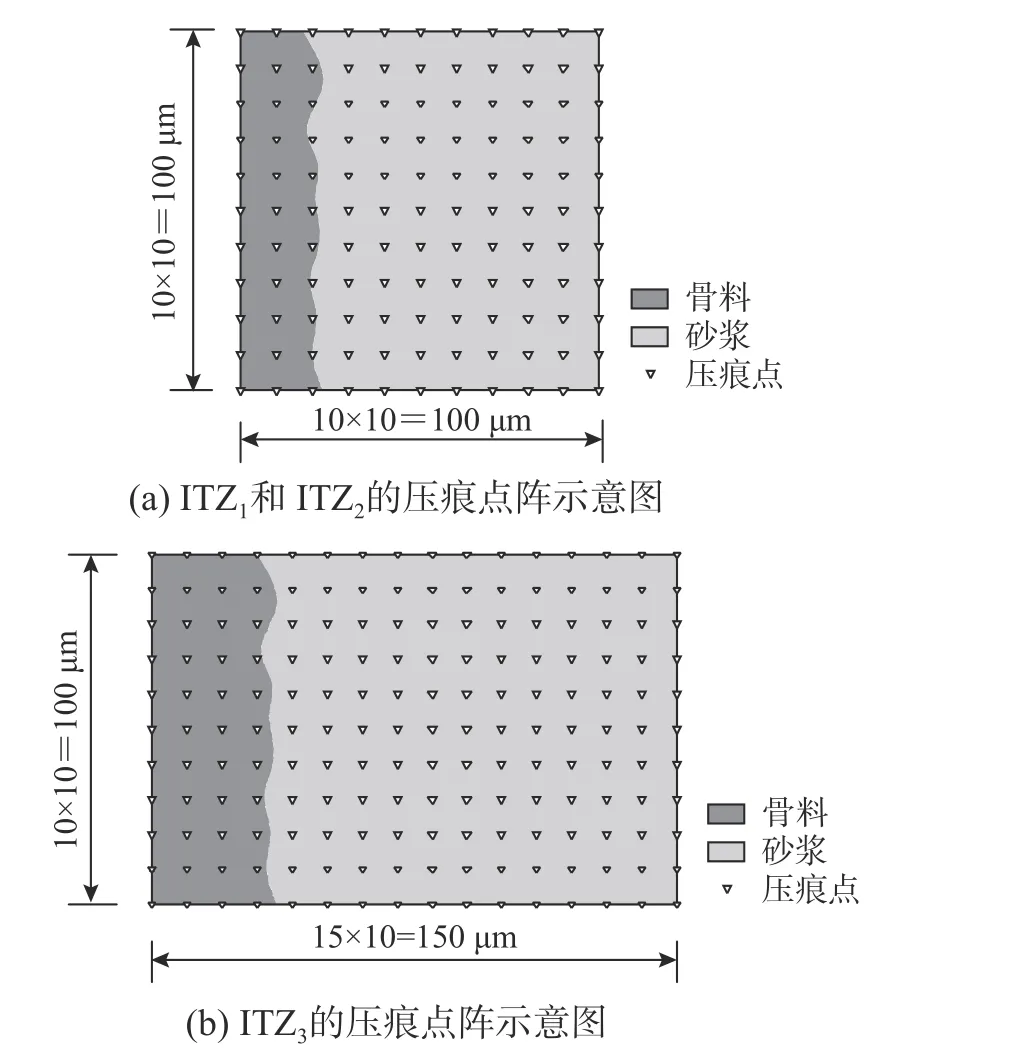
图2 再生混凝土多重界面过渡区压痕点阵示意图Fig. 2 Lattice diagram of indentation in multi interface transition zones of recycled aggregate concrete

2 试验结果和分析

2.1 疲劳破坏现象

普通混凝土疲劳破坏时，表现出明显的脆性破坏特征，各部分破坏体四处崩散，破坏面上残留一些相对摩擦产生的粉末，从破坏面观察可知，较少出现天然骨料破坏的现象，多在骨料和水泥石的接触面上破坏。再生骨料混凝土疲劳破坏特征与普通混凝土相似，但再生骨料混凝土疲劳破坏面上存在较大比例的再生骨料的破坏，见图3。

图3 疲劳破坏面Fig. 3 Fatigue failure surface

掺入纳米SiO2的再生骨料混凝土的破坏过程和最后的破坏模式与未掺纳米SiO2的再生骨料混凝土基本相同，也表现出较大的脆性破坏特征。相比未掺入纳米SiO2的再生骨料混凝土，破坏面从再生骨料穿过的比例增大。

破坏模式与应力水平关系不大，主要分为剪切破坏，锥形破坏和混合型破坏。破坏模式见图4。

图4 混凝土疲劳破坏模式Fig. 4 Failure failure modes of concrete

2.2 疲劳寿命

疲劳寿命是指试件在循环荷载作用下，从开始加载到发生断裂所经过的时间或者疲劳破坏时试件所能承受的最大循环次数，本试验采用疲劳破坏时试件所能承受的最大循环次数定义疲劳寿命。疲劳寿命结果见表4。

表4 疲劳试验结果Table 4 Results of fatigue tests

图5 为各组平均疲劳寿命随应力水平的变化曲线，应力水平S对疲劳寿命N的影响非常显著，各试验组的应力水平从0.75 增加至0.85，每提高0.05，疲劳寿命相比前一应力水平下的疲劳寿命折减大概80%～90%。疲劳寿命在应力水平从0.75 升至0.8 应力水平时，疲劳寿命绝对值骤减，从0.8 应力水平升至0.85 应力水平时，疲劳寿命绝对值减少较小。0.80 和0.85 应力水平下，各组的疲劳寿命平均值相差不大。在0.75 应力水平下，RAC50 和RAC100 的疲劳寿命平均值为NC疲劳寿命平均值的42.8%与71.25%；RAC100-NS的疲劳寿命平均值是NC 疲劳寿命平均值的107.8%，增加7.8%。

图5 平均疲劳寿命N 与应力水平S 关系Fig. 5 Relationship between average fatigue life (N) and stress level (S)

2.3 疲劳寿命的概率统计分布

为了准确地描述疲劳寿命结果，也希望能在工程实际中得到应用，需要对试验数据进行可靠度理论分析，用概率统计方法进行研究，本文采用两参数的威布尔分布函数进行验证，数据更加安全，且便于计算。

采用两参数威布尔分布函数推导出来的保证率p与疲劳寿命之间的关系为：

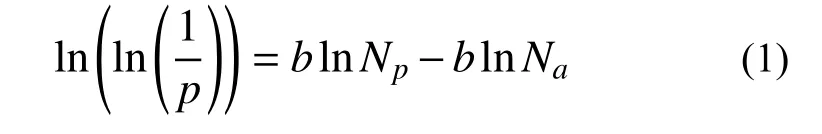
式中：N0为最小寿命参数；Na为特征寿命参数；b为威布尔形状参数；NP为具有保证率p的疲劳寿命。

如果ln[ln(1/p)]与lnNp为线性关系，则可判定样本符合两参数威布尔概率分布。样本疲劳寿命Np对应的保证率p用平均秩来表示，见式(2)。然后确定ln[ln(1/p)]与lnNp是否符合线性关系，并通过拟合曲线得到威布尔分布参数。

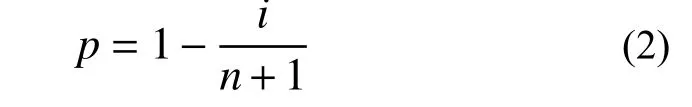
式中：i为由小到大的排列“序数”；n为样本数目；p为第i个样本值xi的保证率估计量。

回归分析得到各试验组lnN-ln(ln(1/p))的关系，限于篇幅，仅列出部分拟合曲线图，见图6。各试验组各应力水平下lnN与ln(ln(1/p))线性关系明显，其线性表达式采用ln(ln(1/p))=blnN+a，表5列出了各组的a与b值，其中a=-blnNa，b为威布尔分布函数的形状参数，Na为威布尔分布函数的特征寿命参数，R为它们之间的线性相关系数。R2表示样本符合威布尔分布的契合程度，由表5可以看出，大部分试验组的相关系数在0.85 以上，具有明显的威布尔分布特性。

表5 威布尔分布参数及R2Table 5 Weibull distribution parameters and R2

图6 lnN-ln(ln(1/p))关系图[RAC100-NS]Fig. 6 lnN-ln(ln(1/p)) diagram [RAC100-NS]

由以上分析可知，采用两参数威布尔函数描述疲劳寿命分布较为准确，因此可采用威布尔分布函数得到考虑保证率p的疲劳寿命。各试验组各应力水平下，设定四个保证率数值，即90%(0.9)、80%(0.8)、70%(0.7)、60%(0.6)，分别计算对应的ln(ln(1/p))结果，代入前面拟合得到的ln(ln(1/p))-lnN方程，即可得到相对应的疲劳寿命，计算见式(3)，考虑保证率p的疲劳寿命见表6。

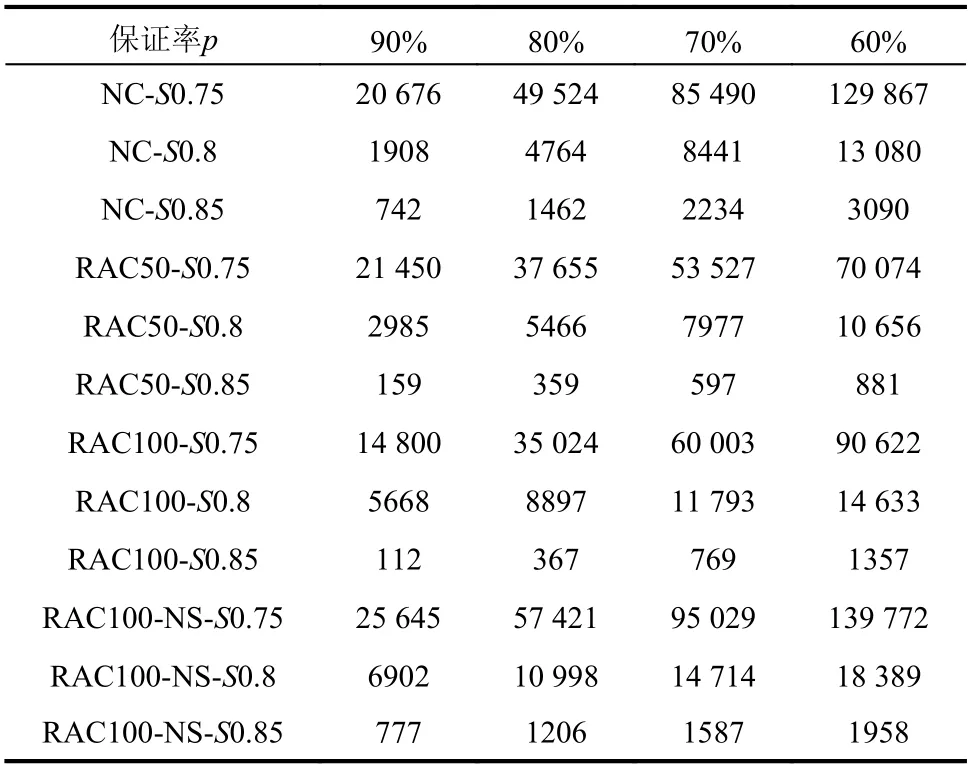
表6 一定保证率下的疲劳寿命Table 6 Fatigue life at certain guaranteed rates

各试验组各应力水平下的疲劳寿命随着保证率的提高而减小，随着保证率的提高，疲劳寿命折减较多。0.75 应力水平，90%保证率下，RAC100-NS 的疲劳寿命比RAC100 和NC 分别高出73%和24%，纳米SiO2对再生骨料混凝土疲劳寿命的提升效果显著。在0.75 应力水平下，采用两参数威布尔分布得到的具有保证率的疲劳寿命，以50%保证率为基准，保证率每提高10%，疲劳寿命降低15%～20%。该关系对0.80 和0.85 应力水平，也较符合。

2.4 疲劳方程及S-N 曲线

S-N曲线或疲劳曲线是疲劳寿命N与应力水平S之间的关系曲线。将一组不同应力水平下承受等幅循环荷载的试件加载至破坏，记录试件的疲劳寿命N，应力水平S与疲劳寿命N的关系曲线，为材料的疲劳曲线。应力水平S是以比值形式定义的无量纲量，可消除混凝土强度、养护条件、加载龄期等条件的影响，采用S-N曲线可较精准地表征材料的疲劳特性，S-N曲线对应的函数方程即疲劳方程。

建立起S与lgN的单对数方程，拟合曲线见图7。各组回归分析得到的疲劳方程的表达式采用S=AlgN+B，疲劳方程及参数见表7，表中R为线性相关系数。

图7 S-N 曲线Fig. 7 S-N curves

表7 单对数疲劳方程及R2Table 7 Single logarithmic fatigue equation and R2

相同的应力水平(相同的纵坐标值)下，函数的横坐标数值越小，疲劳寿命就相应越小，疲劳性能也较差，故图中右上方函数图像对应的试验组，其疲劳性能较好。根据图6，疲劳寿命的排序为NC＞RAC100-SiO2＞RAC100＞RAC50。

由于复杂的界面过渡区、存在缺陷的再生骨料及骨料表面附着的低活性粉末，再生骨料混凝土比普通混凝土的原始缺陷增多，因而相同应力水平下再生骨料混凝土的疲劳寿命比普通混凝土低。王博等[17]在再生骨料混凝土钢筋粘结滑移研究中发现，当再生骨料与天然骨料共存时，由于它们之间的“耦合作用”，随着再生粗骨料掺量的增加，混凝土的初始损伤呈不同程度的增加，其力学性能并非单调变化。本文之所以得到再生粗骨料掺量100%的试验组比50%的试验组疲劳寿命高，这和再生骨料混凝土的疲劳性能比普通混凝土表现出更明显的离散性有关[18]。

图8 对比了Arora 和Singh[19]、肖建庄等[8]和本文中再生粗骨料100%取代的再生骨料混凝土的受压疲劳方程，发现文献[19]的再生骨料混凝土的受压疲劳性能明显较差。各试验中再生骨料的性质如下，文献[8]采用的再生粗骨料表观密度和压碎指标分别为2520 kg/m3、15.2%；文献[19]中再生粗骨料的表观密度和压碎指标分别为2460 kg/m3、25.6%；本文中再生粗骨料的表观密度和压碎指标分别为2669 kg/m3、11%。故文献[19]的疲劳性能差距很可能是薄弱的骨料性质导致的。

图8 RCA100 的S-N 曲线对比Fig. 8 S-N curve comparison of RCA100

由以上分析知，再生骨料混凝土的轴压疲劳性能受再生骨料性质影响较大。再生骨料的掺入对混凝土单轴疲劳性能有两方面影响：再生骨料的掺入对混凝土单轴疲劳性能有两方面影响：当再生骨料表面附着的旧砂浆含量少，压碎指标低，则骨料品质较好，在疲劳加载时，损伤在混凝土非主要破坏面上发展，耗散能量，则表现出好的疲劳性能；若再生骨料压碎指标高，品质较差，混凝土引入缺陷较多，其损伤发展就较快速。而这两者之间的平衡以及相互作用的效果仍需深入探讨。

综合文献[8]与本文疲劳试验数据，得到RAC100的疲劳方程见表8。

表8 单对数疲劳方程及R2Table 8 Single logarithmic fatigue equation and R2

2.5 S-P-N 方程及轴压疲劳强度

2.5.1S-P-N方程

单对数形式的S-N曲线及对应的疲劳方程是没有考虑失效概率的中值疲劳方程，保证率为50%。混凝土疲劳性能具有比其他力学性能更离散的性质，可采用数理概率统计得到的疲劳寿命Np建立与应力水平S间的疲劳方程。

回归分析得到的S-P-N方程表达式采用S=AlgN+B，A与B的数值大小见表9，各保证率下不同试验组的S-P-N曲线见图9。

表9 S-P-N 曲线方程参数及R2Table 9 S-P-N equation parameters and R2

图9 S-P-N 曲线Fig. 9 S-P-N curve

2.5.2 轴压疲劳强度

疲劳强度为材料在无限次交变荷载作用下不发生破坏的最大应力，又称疲劳极限。实际中，材料不会一直承受交变荷载而不发生破坏，试验一般取200 万次作为材料不发生破坏的标准，即材料承受交变荷载的次数超过200 万次，就认为该试件在该应力水平下平下不会发生破坏。

基于S-P-N曲线及疲劳方程得到各试验组的轴压疲劳强度。S-P-N曲线是不同保证率条件下，应力水平S与疲劳寿命N之间的关系曲线，而疲劳强度为材料疲劳寿命为2×106周对应的应力大小。结果见表10。

表10 N=2×106 周时的应力水平S 及轴压疲劳强度Table 10 Stress level S and Uniaxial fatigue strength at 2×106 cycles

50%保证率下，RAC100-NS 的轴压疲劳强度比RAC100 提高9.4%，比NC 低6.2%。对比90%保证率下，各试验组轴压疲劳强度的关系：再生骨料掺量为50%和100%的RAC50、RAC100 的轴压疲劳强度比普通混凝土NC 的疲劳强度降低了1.3%、6.6%。掺入纳米SiO2的再生骨料混凝土RAC100-NS 的轴压疲劳强度比RAC100 提高3.3%；RAC100-NS 的轴压疲劳强度比普通混凝土疲劳强度低3.5%。

2.6 疲劳加载的应变演化曲线和疲劳剩余强度

2.6.1 疲劳加载的应变演化曲线

受压疲劳试验中试件的疲劳应变和残余应变是其内部损伤演化的宏观表征，应变曲线能真实反应试件的损伤规律，可用来评估材料的性能和估计材料的疲劳寿命。通过IMC 动态数据采集仪对试件的应变值进行实时采集，最后得到荷载最大力和最小力时刻对应的疲劳应变和残余应变。图10 中“ εr”为残余应变，“ εmax”为疲劳应变。

图10 残余应变与疲劳应变曲线Fig. 10 Residual strain and fatigue strain curves

图10(a)为再生骨料混凝土(RAC50 与RAC100)与普通混凝土(NC)0.85 应力水平下的疲劳应变与残余应变，再生骨料混凝土与普通混凝土的疲劳应变和残余应变随着循环比的变化并无太大差别，基本相似。虽说再生骨料混凝土与普通混凝土随循环比的应变增长基本同步，但再生骨料混凝土疲劳寿命小，在相同的循环周次的条件下，再生混凝土的应变增长更快。

图10(b)为RAC100-NS 与RAC100 在0.85 应力水平下的疲劳应变和残余应变对比图。应变曲线中第二阶段的斜率主导试件整个应变增大过程的速率，掺入纳米SiO2的再生骨料混凝土第二阶段的斜率变小，应变增大较慢，应变增加速率第一阶段和第三阶段较快，但第二阶段的比例也有所增加，疲劳寿命较大。

2.6.2 疲劳剩余强度

损伤的累积是导致材料宏观力学指标衰减的内在原因，疲劳剩余强度是描述疲劳加载损伤的一种方式。

本文将加载周次设定为各试验组0.8 应力水平下，具有50%保证率的疲劳寿命(即采用5 个试件疲劳寿命的平均值)的20%和70%。各加载周次分别加载3 个试件，按照混凝土轴心抗压强度方法测定试件疲劳剩余强度。各试验组疲劳剩余强度平均值见表11。

表11 疲劳剩余强度平均值Table 11 Average fatigue residual strength

采用较能够反映混凝土强度衰减规律实际情况的剩余强度模型[20-22]对试验结果进行验证，如图11；拟合曲线式(4)，拟合参数见表12。

表12 疲劳剩余强度模型参数Table 12 Residual strength model parameters

图11 剩余强度模型曲线Fig. 11 Residual strength model curve

从图11 可以看出，疲劳剩余强度模型曲线的形状往右上角凸出，但程度稍有不同，凸出程度越小，说明其强度衰减的规律越接近线性，随着循环比的变化，剩余强度的衰减较均匀；凸出程度越大，强度衰减的阶段性可能越突出。而曲线的这种形貌特征与方程中的ν值相关联的，ν值大，凸出明显。对比表12 中的ν值，NC 的ν值稍大于RAC50 和RAC100，但相差不大。掺入纳米SiO2的再生骨料混凝土随着循环比的强度衰减具有较大的不均匀性，后期的强度衰减更加迅速。

2.7 界面过渡区的纳米压痕分析

纳米SiO2改性再生骨料混凝土前后的界面过渡区压痕点阵模量分布云图，如图12～图14 所示。通过统计压痕数据可以得出界面过渡区的界面弹性模量平均值，如表13 所示。

表13 混凝土的界面过渡区参数Table 13 Parameters of ITZ of concrete

图12 ITZ1 的模量分布云图 /GPaFig. 12 Modulus distribution nephogram of ITZ1

图13 ITZ2 的模量分布云图 /GPaFig. 13 Modulus distribution nephogram of ITZ2

图14 ITZ3 的模量分布云图 /GPaFig. 14 Modulus distribution nephogram of ITZ3

从图12～图14 和表13 可以看出，再生骨料混凝土经纳米SiO2改性后，多重界面过渡区的弹性模量均得到了提高；相较于RAC100，RAC100-NS的ITZ1、ITZ2、ITZ3压痕模量分别提高了约3.7 GPa、1.4 GPa、3.0 GPa。主要的原因是纳米SiO2粒径小，活性高，可填充混凝土孔隙，密实浆体结构，与Ca(OH)2发生反应可降低其含量并增加水化硅酸钙(C-S-H)凝胶量，加强浆体与骨料间的界面粘结[13]。因此，掺入纳米SiO2能够有效改善再生骨料混凝土三种界面过渡区的性能，提高界面过渡区的压痕模量。多重界面过渡区性能的改善，减少了再生骨料混凝土的初始缺陷，提高了其疲劳寿命。

3 结论

通过对比纳米二氧化硅改性前后再生骨料混凝土的疲劳性能及其多重界面过渡区细观力学性能，可得到以下结论：

(1)再生骨料混凝土以及纳米SiO2改性的再生骨料混凝土的轴压疲劳破坏均为脆性破坏。

(2) 与普通混凝土相比，再生骨料混凝土的受压疲劳寿命低，而纳米SiO2的掺入可显著提高再生骨料混凝土的受压疲劳寿命，RAC100-NS 疲劳寿命平均值比RAC 提高了7.8%。

(3) 对比轴压疲劳应变曲线、残余应变曲线及轴压疲劳剩余强度模型曲线，发现掺入纳米SiO2的再生骨料混凝土表现出更快速的第三阶段损伤。RAC100-NS 的剩余强度后期衰减较大，非线性规律明显。

(4) 纳米压痕分析显示，纳米二氧化硅的掺入提高了多重界面过渡区的压痕模量。相较于RAC100，RAC100-NS 的ITZ1、ITZ2、ITZ3压痕模量分别提高了约3.7 GPa、1.4 GPa、3.0 GPa。

(5) 再生骨料混凝土的单轴受压疲劳寿命服从两参数的威布尔概率分布，基于威布尔概率分布得到S-P-N单对数方程及轴压疲劳强度，可供工程应用参考。