卡尔曼滤波短时交通流预测普通国省道适应性研究*

申雷霄 陆宇航 郭建华▲

（1.江苏省徐州市公路管理处 江苏 徐州221002；2.东南大学智能运输系统研究中心 南京210018）

0 引言

伴随经济的快速发展，交通设施的供给愈来愈难以满足快速增长的交通出行需求，导致许多亟待解决的问题，如交通拥堵、交通安全、能源消耗和环境污染等。普通国省道是我国综合交通体系的重要组成部分，对满足我国地面交通运输需求具有重要的意义。我国普通国省道建设周期长、成本高，改扩建不易，所以，在不扩大普通国省道建设规模的前提下，如何有效地提高普通国省道的服务能力，满足日益增长的交通需求，成为当前普通国省道交通运行管理和控制的重点工作和未来发展方向。

智能运输系统（intelligent transportation system，ITS）在普通国省道的交通管理中具有广泛的应用前景。ITS是在传统的交通运输系统基础上，采用先进的计算机、信息、通信、人工智能等高新技术，扩展和丰富交通运输系统的内涵，形成实时、高效、准确的新型运输系统[1]。短时交通流预测能够预测未来的交通流状况，可帮助出行者规划出行，降低个人出行时间和费用，并以此为依据指导交通管理者制定合理的交通管制方案，以缓解交通拥堵，减少交通事故的发生，提高路网运输效率，使交通管理控制由被动转向主动，是提高智能运输系统可靠性、安全性的关键所在，也是智能交通系统建设中必不可少的基础性技术。

长期以来，短时交通流的预测技术领域取得了诸多的研究成果与方法，包括线性模型、非线性模型、混合模型和其他模型等[2]，并在特定的情境下得到了验证，如高速公路环境、城市道路环境等。然而，对普通国省道而言，其分布地域广，往往与港口、枢纽、风景区、工业园区等重要设施相连，周边情况复杂，导致交通流特征与水平具有显著的差异。这就要求短时交通流预测方法具有良好的适应性，能够针对不同地点、不同时间的交通流进行有效的预测。否则，若短时交通流预测方法不能适应交通流的变化，只能够在一处或几处路段进行流量预测，将会大大提升短时交通流预测算法的实施成本，降低算法的实用性和应用价值。

为此，笔者针对普通国省道交通流短时预测算法的适应性开展研究。选用自适应卡尔曼滤波算法（adaptive Kalman filter algorithm）[3]预测短时交通流的均值，给出预测区间，并对算法的适应性进行深入分析，揭示算法的自适应机制，为普通国省道的交通管理和控制措施提供技术支撑。

1 现状分析

短时交通流预测主要包括短时交通流均值预测以及区间预测，前者主要是预测短时交通流的均值，而后者主要围绕预测的均值，给出一定置信水平下的预测区间。分别对短时交通流量均值和区间预测的方法进行现状分析和总结。

1.1 均值预测方法

短时交通流均值预测领域的研究较多，目前已经提出许多预测方法，常见方法有历史平均法、指数平滑法、局部加权线性回归法、神经网络法、K近邻法、随机时间序列、混合算法等。

历史平均、指数平滑、局部加权线性回归等是早期的预测算法。历史平均算法是1种简单快速的预测方法，刘静等[4]提及其早在1981年就被广泛应用于城市交通流预测，以构建动态路径诱导系统和出行者信息系统。指数平滑在城市交通流量、铁路旅客运送量等场景中应用较多，通过不同时刻流量观测值的不同权重，使预测值有效地反映预测对象的实际状况变化，郭良久等[5]研究高速公路出行在各个节假日的变化特征，通过指数平滑算法预测节假日期间的高速公路出行总量。局部加权线性回归算法考虑不同交通流参数的影响，建立过去、当前及未来交通流之间的回归关系，高洪波等[6]基于分形插值的指数平滑算法进行实际交通流预测，结果表明预测精度良好。上述算法结构简单，然而适应性较弱，难以满足不同场景下的高精度短时交通流预测需求。

神经网络和K近邻是典型的非参数预测方法。神经网络具有较强的学习能力、容错能力和自适应能力，适合求解机制复杂的问题，近年来被广泛应用于智能控制、信号处理、模式识别及预测管理等领域，如李桃迎等[7]把高速公路的交通流、天气状况等特征参数作为输入，以交通流量作为输出，实现对高速公路交通流的预测。K近邻预测算法采用相似性度量函数进行模式识别，搜索相近历史状态后对交通需求进行预测，如谢海红等[8]在使用模式距离搜索方法上改进K近邻算法进行短时交通流预测，提升了预测精度；Meng等[9]通过优化K近邻预测算法的搜索时间预测未来的交通流，有效提高了实时搜索速度。上述算法具有一定的自适应特性，预测精度相对较高。

随机时间序列是经典的预测算法，如差分整合自回归移动平均（autoregressive integrated moving average，ARIMA）模型等。该算法能够有效地运用历史数据推测对象的发展趋势，也可考虑偶然因素导致的随机性，高效易行、精度较高。B.Williams等[10]依据Wold分解原理，建立了短时交通流均值预测的季节性差分整合自回归移动平均（seasonal autoregressive integrated moving average，SARIMA）模型。基于SARIMA模型，Guo等[3]应用状态空间分析及实时滤波理论，提出了自适应卡尔曼滤波算法，同时，Guo等[11]分析了交通流时间汇集间隔的影响，发现随机时间序列的预测精度会伴随时间间隔的增加而逐渐提高。韩超等[12]采用ARIMA（p，d，0）模型结构的时间序列分析方法，构建了1种短时交通流实时自适应预测算法。

混合预测算法也得到了广泛的关注。刘钊等[13]提出了1种K近邻算法和支持向量回归混合预测模型，研究表明该模型优于单一预测模型。冯微等[14]提出了1种基于受限玻尔兹曼机-深度置信网络的混合预测方法，预测精度高。梅朵等[15]提出1种时空遗传粒子群和支持向量机混合预测模型，相对误差稳定且预测精度有所提升。上述混合预测算法同样具有一定的自适应特性，预测精度相较于单一预测方法较高。

1.2 区间预测方法

和短时交通流均值预测方法相比，短时交通流量区间预测方法研究较少，主要有广义自回归条件异方差（generalized autoregressive conditional heteroscedasticity，GARCH）模型、模糊信息粒化算法和随机波动（stochastic volatility）模型。

GARCH模型源于R.E.Engle[16]提出的ARCH模型，由T.Bollerslev[17]扩展为GARCH模型。该模型起初在金融时间序列分析中得到广泛应用，后续逐渐应用在交通领域，在估计交通流序列方差的基础上进行区间预测。首先，针对交通流的不确定性，Guo等[18]提出了1种综合异方差检验方法，通过实际交通流数据分析，发现交通流时间序列的条件方差随时间变化而发生明显变化，条件异方差性显著，在此基础上，Guo等[3,19]分别针对交通流速度序列和交通流量序列，建立分层卡尔曼滤波预测算法，实时处理GARCH模型，实现了预测区间在线计算，并提出了预测区间的评价标准。模糊信息粒化方法采用模糊逻辑和信息粒化的方法提取并压缩时间序列中的信息，是1种建立在模糊理论上的区间预测方法。王晓全等[20]在虑了交通流时间序列的异方差性的基础上构建ARIMA-GARCH-M组合模型，大幅提升了交通流预测精度。凌墨等[21]构建SARIMA+GARCH模型分析交叉口交通流的不确定性，得到不同交通流不确定下的交叉口信号配时方案。

和广泛应用的GARCH模型相比，模糊信息粒化方法和随机波动模型也得到了应用。Guo等[22]通过模糊信息粒化方法，将短时交通流均值预测的问题转化为区间预测问题，即把交通流时间序列粒化为区间序列，采用常规的K近邻预测算法、BP神经网络模型和支持向量机算法，分别对区间的上限和下限进行预测，进而构建预测区间。随机波动模型将交通流不确定性视作隐含的一阶马尔可夫模型，用以量化计算交通参数的不确定性，如出行时间[23]和行程速度[24]等。

1.3 小结

当前短时交通流预测方法已经有众多研究成果。然而，当前研究主要是针对特定场景下的预测算法性能分析，对不同场景下的性能比较和算法特征等适应性分析缺少系统性研究，难以明确研判短时交通流预测方法的适应性。因此，笔者选取自适应卡尔曼滤波算法，采用实际的普通国省道交通流数据，研究其适应性，以预测普通国省道短时交通流的变化状况，满足智能化普通国省道交通管理的需求。

2 自适应卡尔曼滤波短时预测方法

2.1 算法原理

自适应卡尔曼滤波算法将交通流时间序列的均值视作季节性变化特征和短期变化特征的叠加，并考虑交通流时间序列的随机波动特征以计算预测值的预测区间，分别用季节指数平滑模型、ARMA（1，1）和GARCH（1，1）模型表示，如下所述。

2.1.1 季节指数平滑模型

季节指数平滑模型主要捕捉交通流时间序列均值的季节性变化特征，其模型见式（1）。

2.1.2 短期变化模型

短期变化模型主要捕捉交通流时间序列均值的短期变化特征，本文采用ARMA（1，1）模型，见式（2）。

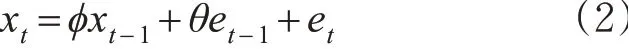
式中：xt为t时刻交通流季节状态观测值，辆/15 min；xt-1为t-1时刻交通流季节状态观测值，辆/15 min；φ为自回归参数；θ为移动平均参数；et为t时刻的交通流噪声，辆/15 min；et-1为t-1时刻的交通流噪声，辆/15 min。针对ARMA（1，1）模型，首先，可将ARMA模型参数作为待估计状态，采用随机游走模型定义状态转移方程，见式（3）。

然后，将交通流量序列作为观测过程，定义观测方程，见式（4）。

式中：wt为t时刻状态变量(φ θ)T；T为转置矩阵；Φt为状态转移矩阵为遗忘因子，本文取0.999；at为t时刻状态噪声为t时刻的观测矩阵(xt-1et-1)的转置矩阵。由此可见，联立式（3）~（4）构成短期交通流变化的状态空间方程，可以使用卡尔曼滤波方法求解。

2.1.3 随机波动特征模型

采用GARCH（1，1）捕捉交通流时间序列的随机波动特征，主要描述交通流噪声平方项的演化规律，用以构造均值预测的预测区间，模型定义见式（5）。

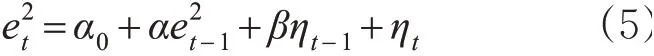
式中：α0，α，β为模型参数为t时刻交通流噪声值的平方为t-1时刻交通流噪声值的平方；ηt为t时刻波动性特征噪声；ηt-1为t-1时刻波动性特征噪声。同样，针对上述模型，可定义观测方程见式（6）。

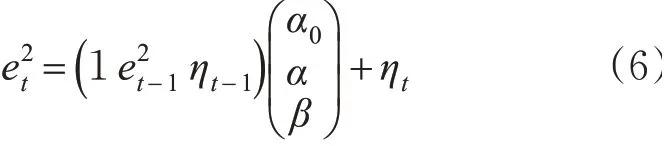
采用随机游走模型定义系统状态方程见式（7）。

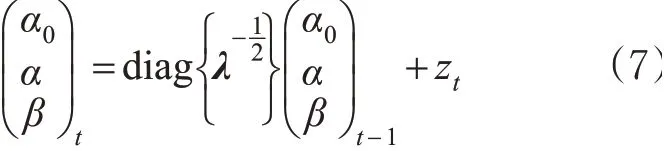
式中：zt为t时刻系统状态噪声；λ为遗忘因子，本文取0.999。这样，联立式（6）~（7），构成交通流时间序列随机波动的状态空间方程，可以采用卡尔曼滤波方法求解。

2.2 自适应卡尔曼滤波递归步骤

如前所述，可将交通流时间序列的均值视作季节性变化特征和短期变化特征的叠加，并考虑交通流时间序列的随机波动特征，得到季节指数平滑模型和2个状态空间模型，前者可实时求解，而状态空间模型可通过卡尔曼滤波求解。为提升适应交通流变化的能力，采用自适应卡尔曼滤波方法，以根据观测噪声和系统噪声对卡尔曼滤波参数进行实时调整。

针对一般状态空间方程组，有

式中：wt为t时刻状态变量(φ θ)T；Φt为t时刻状态转移矩阵；wt-1为t-1时刻状态变量(φ θ)T；at为t时刻状态噪声；Xt为t时刻的观测矩阵(xt-1et-1)；Yt为t时刻的观测值。则自适应卡尔曼滤波方法的具体步骤如下。

步骤1。先验状态估计和协方差矩阵估计。

步骤2。观测误差计算。

步骤3。观测过程协方差矩阵更新Rt。

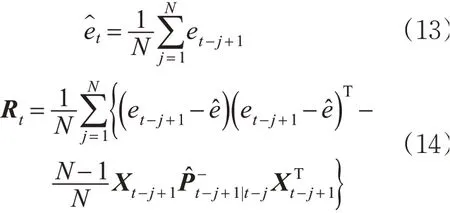
步骤4。卡尔曼增益计算。

步骤5。后验状态估计和后验协方差矩阵估计。

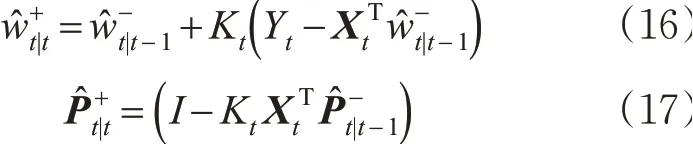
步骤6。状态误差计算。

步骤7。状态过程协方差矩阵更新Qt。

3 实验设计

3.1 数据采集

为展示自适应卡尔曼滤波算法的适应性及预测性能，需要选取普通国省道不同地理位置处的历史交通流数据进行分析和验证。以徐州市普通国省道为研究对象，截至2020年底，徐州普通国省道总计1 386.482 km，其中一级公路1 024.798 km，二级公路361.684 km。在该路网上，为掌握路网的交通运行状况，在不同的地理位置设立交通量调查站，以实时采集路网交通流数据。本文选取徐州市普通国省道上8个交通调查站作为交通流数据采集点，覆盖不同的地理位置，且交通特征各有差异。针对选定的交通调查站，获取历史交通流数据，对交通流数据进行数据清洗和汇集后，得到满足算法输入需求的交通流数据。

3.2 算法预测性能适应性分析

为展示自适应卡尔曼滤波算法的预测性能适应性，需要对算法的均值预测结果和区间预测结果进行评价。本文使用平均绝对误差（MAE）、平均绝对百分比误差（MAPE）以及均方根误差（RMSE）作为均值预测性能评价指标，使用无效覆盖率KP和宽度流量比Ri作为区间预测性能评价指标，定义见式（21）~（25）。

3.3 算法适应性机制分析

算法适应性机制分析主要包括2个方面。①针对卡尔曼滤波的参数，通过展示各个参数在预测过程中的收敛及稳定过程，体现卡尔曼滤波算法在预测过程中的自适应变化机理和过程，以满足不同地点、不同时间路段上的预测需求。②针对卡尔曼滤波的预测结果，通过展示预测结果在预测初期向稳定期的变化过程，体现算法在不同交通流水平下的预测调整和收敛过程。

4 实例分析

4.1 数据采集

数据来源于徐州市丰县S254沙河、贾汪G206江庄、沛县G518鹿楼等8个交通调查站，采集时间为2020年10月1日—12月31日，汇集度为15 min，并通过SAS 9.4软件，采用SARIMA模型对缺失数据进行补齐。各交通调查站的车道数、起始时间和终止时间等基本信息见表1，各交通调查站的地理分布状况见图1。

表1 检测地点说明Tab.1 Description of test sites

图1 交通调查站分布Fig.1 Distribution of traffic survey stations

4.2 预测性能适应性分析结果

应用所选的自适应卡尔曼滤波算法对2020年10月22日—12月31日的交通流量进行预测，得到均值预测和区间预测的性能指标见表2。需要说明的是，在计算性能指标时，为排除卡尔曼滤波算法收敛过程的影响，前3个星期的数据没有计算在内，此外，低于400辆/15min的交通流数据也排除在外，以重点关注算法在交通流水平较高时的性能。

从表2可见：对均值预测性能而言，各交通调查站的MAE、MAPE和RMSE在大部分时间段内较小，如MAPE在10.98%~15.92%之间，说明预测结果较为准确，所选算法可以较好的预测交通流的均值。对区间预测性能而言，各交通调查站的KP在5.21%~6.15%之间，表明大部分交通流预测值落在95%置信度的区间，同时宽度流量比Ri值很小，表明预测区间较为准确。因此，整体看来，所选算法能够适应不同地点交通流预测的需求。

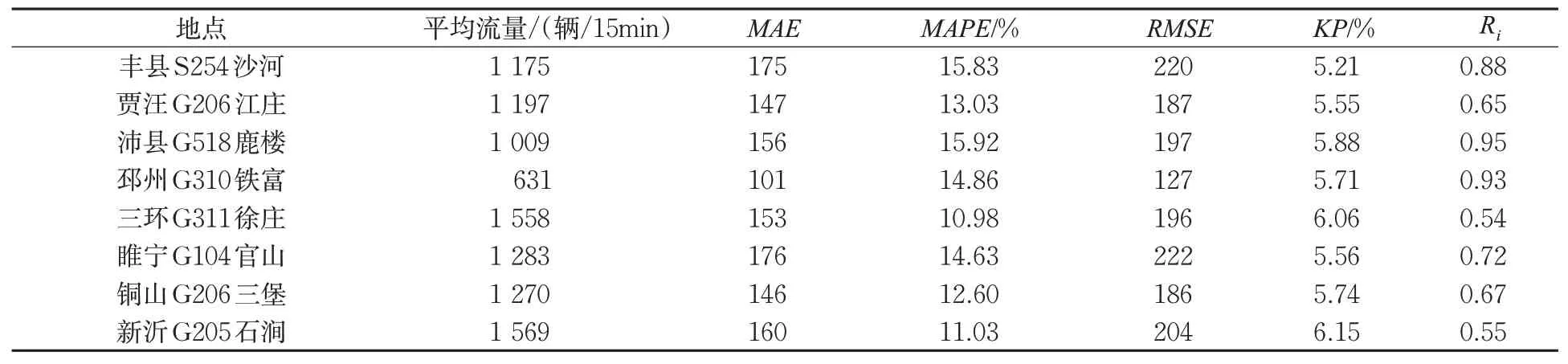
表2 性能指标结果Tab.2 Results of performance indices

为进一步说明所选的自适应卡尔曼滤波算法的预测效果，展示各交通观测站2020年12月31日的交通流短时预测均值和预测区间结果，见图2。

从图2可见：对均值预测而言，8个交通调查站的均值预测值曲线和观测值曲线的趋势和波动都保持一致。如图2（a）丰县S254沙河的交通流量预测图中，观测值在08：00早高峰附近存在较大的流量变化，预测值也能够快速反映趋势变化，而在12：00—16：00交通流量平稳时，预测曲线和观测曲线趋势也能保持一致。此外，与图2（a）中的高流量水平不同，图2（d）邳州G310铁富的交通流量水平偏低，而各个时间段的均值预测值曲线和观测值曲线趋势同样能保持一致，实现实时追踪变化。这表明所选算法能适应不同流量水平的均值预测需求。

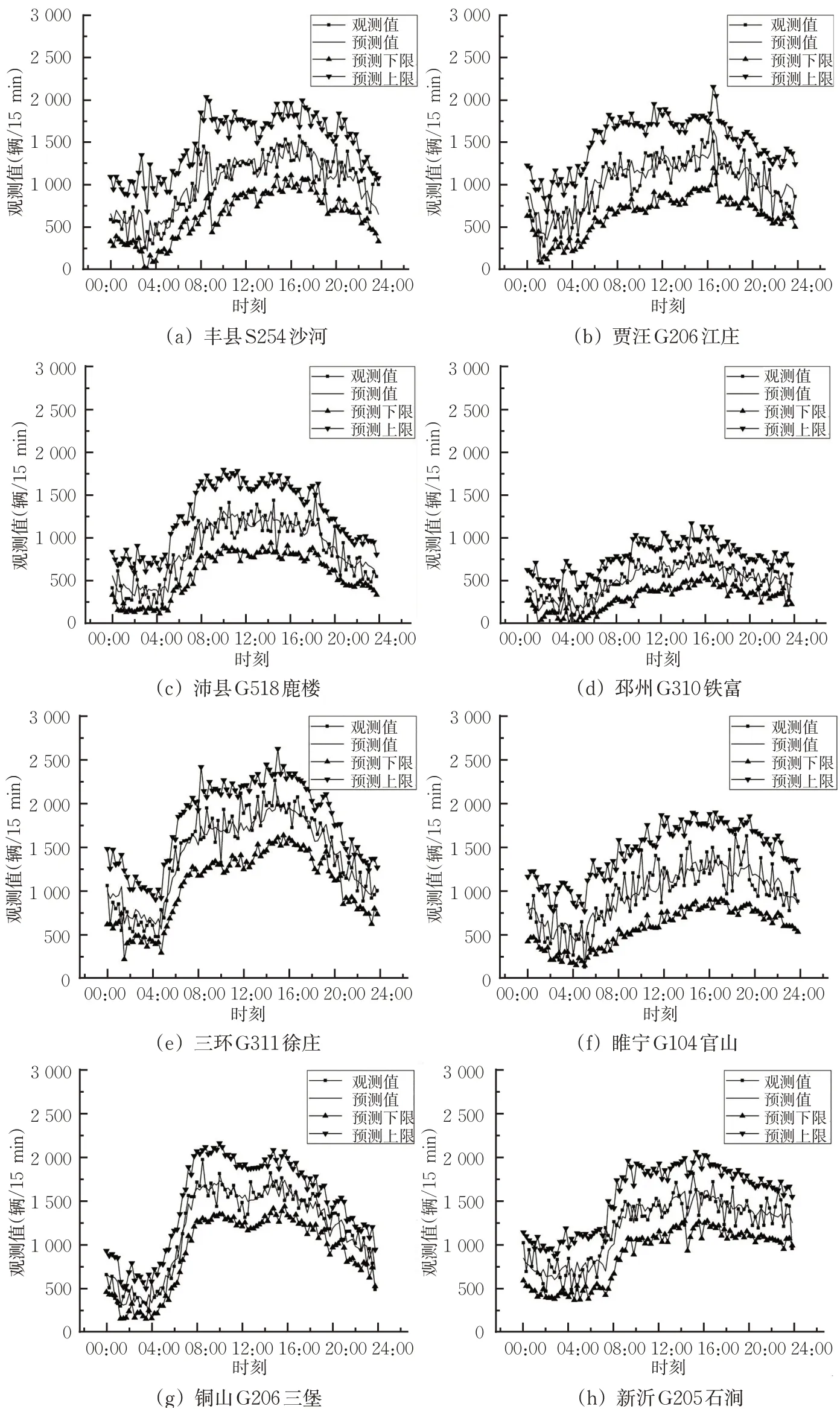
图2 交通流预测图Fig.2 Forecasting of traffic flows

对区间预测而言，在不同时间、不同流量水平下，8个交通调查站的预测下限曲线和预测上限曲线所形成的预测区间可以包围观测曲线，且同样能够在不同观测站点、不同时间、不同流量水平下跟踪交通流量的变化趋势。这表明所选算法能够适应不同流量水平的区间预测需求。

综上所述，所选的自适应卡尔曼滤波算法均值预测和区间预测都表现出良好的性能，且同时体现出算法具备流量趋势追踪能力，表明所选算法的普通国省道短时交通流预测适应性良好。

4.3 算法参数适应性机制分析

通过展示预测过程中算法参数的变化状况，进一步分析算法的适应性机制。选取丰县S254沙河和贾汪G206江庄2个交通调查站，绘制参数变化曲线见图3。

从图3可见：首先，同一地点的不同参数在预测过程中都在不断调整变化。如丰县S254沙河交通流量预测过程中，算法参数φ首先保持初始值0.8，然后从2020年10月8日—11日间急剧波动调整，在2020年10月11日后稳定在0.5附近小幅波动。同样可见，算法参数θ首先保持初始值0.2，然后从2020年10月8日后快速下降至-0.42，并持续调整，体现出不同的参数变化模式。

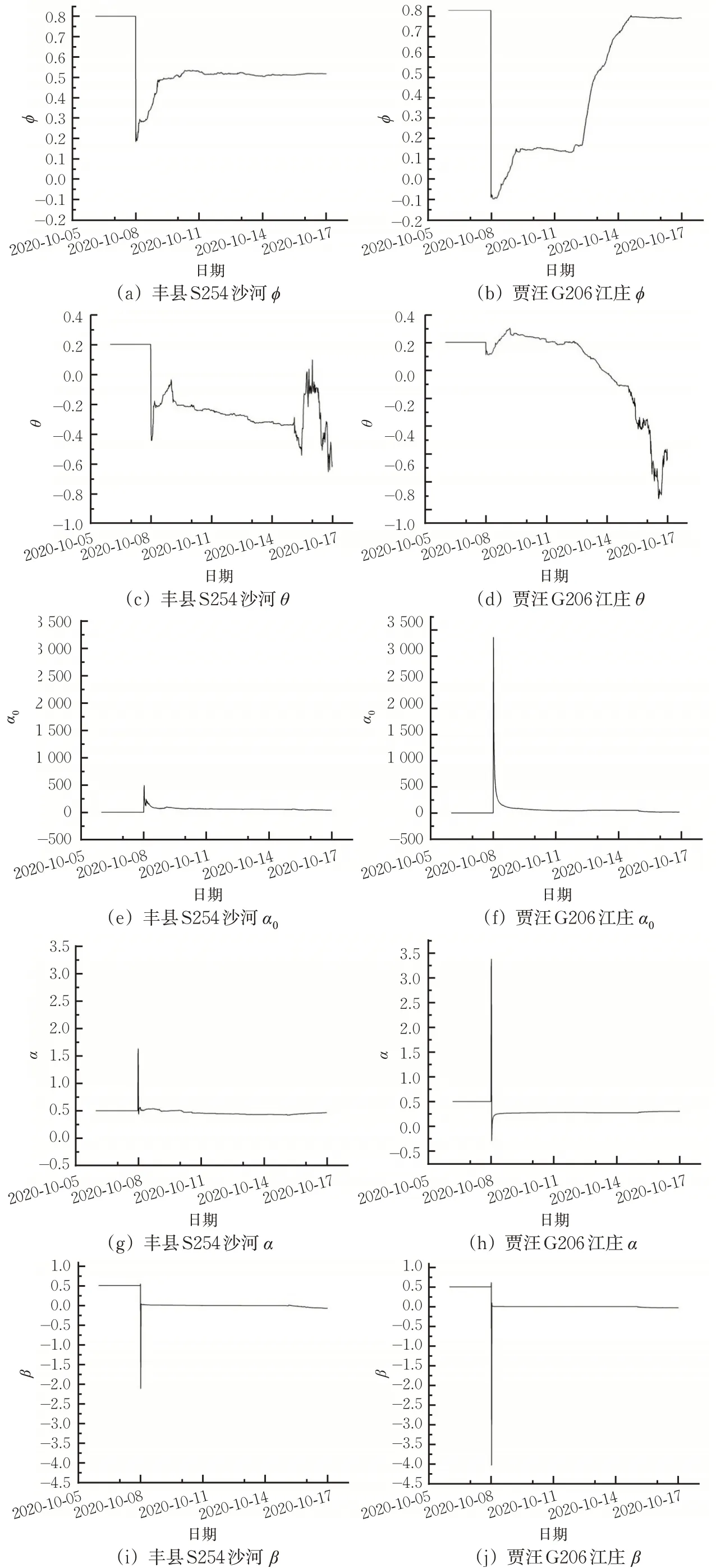
图3 参数变化特征曲线Fig.3 Characteristic curves of parameter change

其次，不同地点的同一参数在预测过程中变化状况也不相同。如算法参数α0在丰县S254沙河交通流量预测过程中，由初始值0.5开始，迅速变到峰值489，再快速降低至40附近波动，而同一参数在贾汪G206江庄交通流量预测过程中，由初始值0.5开始，变到峰值3 346，然后再快速降低至16附近波动。同样可见，算法参数α在丰县S254沙河交通流量预测过程中，由初始值0.5变到峰值1.6，再快速降低至0.45附近波动，而同一参数在贾汪G206江庄交通流量预测过程中，由初始值0.5变到峰值3.4，再快速降低至-0.3后，上升至0.3附近波动。

最后，需要说明的是，对8个交通调查站序列而言，各个相同参数的初始值都相同，而在预测过程中，各参数又都呈现出不同的变化规律，并收敛到不同参数波动水平，表明所选算法能够有效学习不同地点的交通流变化特征，并反映在参数的变化规律之中。

4.4 算法预测初始期自适应收敛分析

4.3展示了所选算法参数的自适应变化特征，为进一步分析所选算法在预测初期的自适应收敛过程，展示各交通观测站在预测初期的观测值与预测均值的变化状况，见图4。

从图4可见：各交通调查站初始预测值和观测值都偏差很大。如对图4（a）丰县S254沙河而言，在预测初期可以看出预测曲线和观测曲线的偏差明显，其中第1个15 min的观测值为922辆/15 min，而预测值为3 776辆/15 min，偏差巨大。随着时间的推移，预测值和观测值在不断接近。如对图4（a）丰县S254沙河交通调查站，至2020年10月9日，可看出预测曲线和观测曲线基本重叠交织。上述观察表明，所选算法通过自适应调整后，预测值可不断趋近观测值。

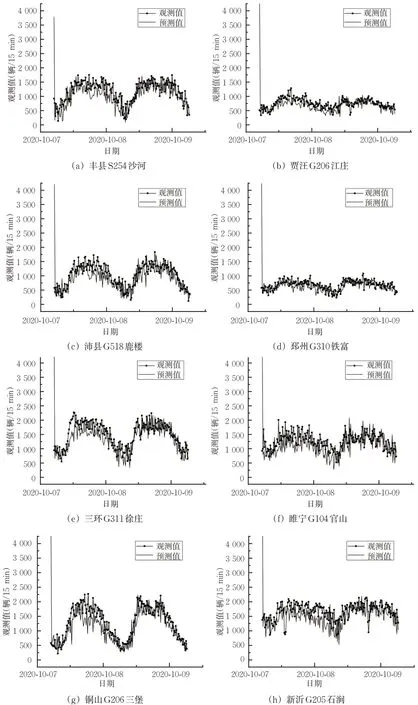
图4 预测结果变化特征曲线Fig.4 Characteristic changing curves of forecasting result

同样，对流量水平偏低的图4（d）邳州G310铁富交通调查站可见同样的规律。对该交通调查站，第1个15 min的观测值为587辆/15 min，而预测值为4 535辆/15 min，且第1 d内预测偏差都较为明显，然而，伴随算法的自适应调整，至2020年10月9日后同样达到预测曲线和观测曲线的交织重叠，实现了二者趋势的一致变化。

综上所述，预测初期的预测曲线收敛变化特征表明，在不同交通流水平下，所选算法的预测性能可进行有效的自适应调整，并最终达到和观测值变化保持一致的状态，体现了算法的自适应性。

5 结束语

普通国省道具有分布地域广、情况复杂的特点，要求短时交通流预测算法具有适应性。为此，笔者选择1种自适应卡尔曼滤波短时流量预测算法，选取江苏省徐州市普通国省道交通观测站，获取实际历史交通流数据，进行系统性的算法适应性分析，得到以下结论：①所选算法具有良好的适应性和预测性能，算法所给出的交通流均值预测值及预测区间能够和实际的交通流变化趋势保持一致，可满足普通国省道的短时交通流预测的要求；②所选算法的自适应性来源于算法参数在预测过程中的不断调整，不同地点同一参数及相同地点不同参数的分析发现，参数调整变化的规律和幅度都不相同，表明所选算法可有效学习不同条件下的交通流变化规律，体现了算法的自适应性；③所选算法在预测初期可实现有效的预测调整和收敛。

短时交通流预测算法众多，本文仅针对特定算法进行了适应性研究，后期可对其它交通流短时预测算法展开适应性研究。同时，可对所选算法开展实际应用和优化，以更好的满足普通国省道智能化交通管理的需求。