基于ADMM-GBS的智能电网多供电商多用户实时定价策略

杨楚越

(上海理工大学 管理学院，上海 200093)

0 引 言

随着日益增长的用电需求、设备老化、不可再生能源的浪费与减少等一系列亟待解决的问题，都在迫切推动着传统电网改进[1]。智能电网采用自动化信息与通信技术，有效提高电力生产和传输效率，较传统电网更高效、更可靠、更经济、更具可持续性[2-3]。需求响应是智能电网的主要管理手段之一，有助于电力市场供需平衡，为需求侧提供低成本、高质量、个性化的服务[4-5]。实时电价是一种根据实际供需情况，连续反映电力边际值的定价机制，理论上是最合理的定价机制。在需求侧安装的智能电表，能够代表用户参与到电力市场竞争中，在各定价时段给出及时的反馈信息[6]。

基于需求响应的用电优化策略研究，按研究对象可分为用户侧和供电商侧两类；按照研究目的又可分为以社会福利最大化、社会福利均衡、用户或供电商成本最小化等多种目标。

文献[7]针对社会福利最大化模型，研究了模型中最小发电量的作用，得到了去掉最小发电量约束的等价模型。文献[8]在将用户分为家庭、工业、和商业3类的基础上，使用多类效用函数，模拟不同用户的用电偏好，打破了以往仅考虑单一效用函数的局限。文献[9]以最小化电网峰谷差为目标，考虑在线电量波动，利用同步扰动随机逼近算法，求解实时定价问题。文献[10]用马尔可夫决策过程表示电器与可再生能源的发电量，引入权重因子作未知变量，平滑用户用电效用与支付成本，构建了用户福利最大化模型。文献[11]考虑用户新能源发电的不确定性，同时定义用户用电量在相邻时段的联系，以社会福利最大化模型为目标，进行实时定价问题的求解。

文献[12]基于传统单供电商多用户情形下拉格朗日对偶及分布算法，考虑多供应商多用户系统中用户侧的电器分类具有时间耦合性，将原问题分解为单一时隙单一供电商情况下的多个子问题。在此基础上，文献[13]将用户家用电器细分为3类，建立多供电商多用户的社会福利最大化模型，但事实上该模型并未实现不同供电商不同电价，不属于严格意义上多供电商问题。

交替方向乘子法(alternating direction method of multipliers, ADMM)[14]综合了乘子法的良好收敛性与对偶上升法的可分解性，在解决分布式凸优化问题上简单有效。算法在智能电网中的研究与应用多集中于解决电网优化调度问题。

现有文献中，鲜有将ADMM算法应用于解决多供电商的电网调度及定价等问题中，对于电力系统，也未考虑用户侧在每日用电中的心理电价限制与每日总电费限制。为此，本文考虑电网系统的多供电商情况，将ADMM-GBS算法应用于实时定价中。模型考虑将家用电器分为必运行电器、弹性电器以及半弹性电器3类，并对电器添加根据用户心理电价变化的启停变量；同时考虑用户的每日总电费限制；在用户配备蓄电池与可再生能源装置发电的情况下，构建以全天多时段的社会福利最大化为目标的模型。通过对原问题的3层分解，将原问题分解为各用户与各供电商各自需求解的子问题。在单个时隙，用户与供电商之间仅需传递电价、用户侧总购电需求信息；在求得各时隙最优供电商发电量、电价、用户用电策略的同时，有效地保证了供需两侧的信息安全性、隐私性，达到了降低电网负载、平滑负载曲线、削峰填谷的目的。

1 系统模型

1.1 用户电器分类

将用户家用电器依据使用时间与电价敏感性分为必运行电器、弹性电器与半弹性电器。

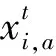
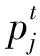
∀i∈N,∀t∈T,∀a∈Ai,2

(1)

(2)

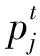
(3)

(4)

1.2 用户蓄电池与可再生能源发电

(5)

(6)

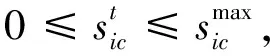
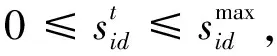
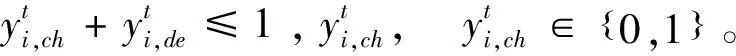
∀i∈N,∀t∈T

(7)

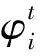
1.3 用户每日预期电费

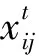
(8)

用户i在时隙t需从各供电商处购买的总电量与自身用电需求之间的关系如式(9)：

(9)

1.4 简化约束条件

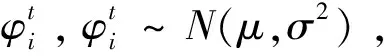
其中，η与ε为极小的正数，表明用户i在时隙t时，弹性电器的用电量大于上限的概率极小。带入切比雪夫不等式推导可得：

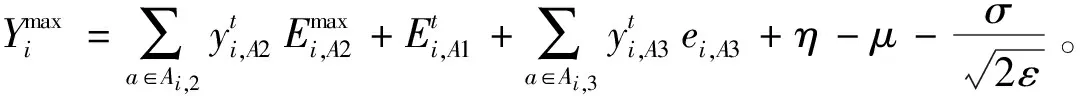
(10)

(11)

其中：

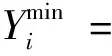
2 社会福利最大化模型

采用二次效用函数来描述用户用电满意度与用电量的关系。

用户效用函数U(x,ω)是非减函数，且边际效用时非增函数。其中，x表示用户的用电量水平，参数ω表示用户不同时刻的用电偏好。

对于供电商，C(L)为其成本函数，其中L是供电商的供电量。C(L)成本函数是增函数且为严格凸函数。不考虑供电商发电有功平衡、爬坡速率、运营成本等约束，供电商成本函数用二次函数表示为：

C(L)=aL2+bL+c

其中，a>0，b,c≥0为预设参数。

考虑多供电商环境，对供电商存在统一调度管理，其供电商之间不存在竞争关系。将一天多时段的社会总福利值表示为用户总效用与供电商总成本的差值，以最大化社会福利值为目标函数：

(12)

社会福利最大化模型可表示为：

(13)

s.t.(7)(8)(10)(11)(12)

其中，约束(7)描述了用户蓄电池从初始状态至时隙t的总充放电量与电池容量、初始电量的关系；约束(8)描述了用户的每日总电费不超过一个上限；约束(10)和(11)确保用户每天购买电量，能够满足家用电器、蓄电池的最低需求，并限制了用户各时隙总购电、充放电量范围；约束(12)为用户购电量与供电商发电量供需平衡约束，是该优化问题的主要约束。约束(7)、(8)、(10)均为关于时间耦合的约束，体现了变量随时间累计的特点。

对于上述优化问题，其目标函数(13)为连续可微的严格凹函数。根据约束条件，其可行域为非空闭凸集，该优化问题为严格凸规划问题，存在唯一全局最优解。

3 分布式实时定价算法

3.1 松弛时间耦合

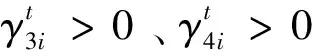
(14)

s.t.(11),(12)

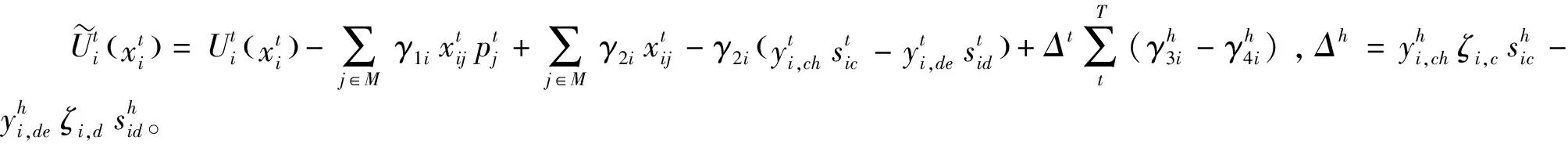
拉格朗日乘子按如下迭代式进行更新：

(15)

(16)

(17)

(18)

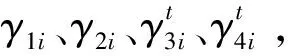
(19)

s.t.(11),(12)

是一个单时隙上的多用户多供应商问题。

3.2 松弛供电商耦合

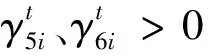
s.t.(12)

其中:

(20)

(21)

拉格朗日乘子按如下迭代式进行更新：

(22)

(23)

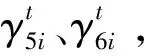
(24)

3.3 ADMM-GBS分布式算法求解单时隙上子问题

考虑更一般形式的带线性约束的可分离凸规划问题：

xi∈Xii=1,…,m

其中，θi(xi)是闭凸函数，Xi是闭凸集。对于上述变量多于两个(m≥3)的凸规划问题，ADMM算法无法保证其结果的收敛性。

ADMM-GBS算法(ADMM based on Gaussian back substitution)是基于ADMM算法提出一种带回代的交替方向收缩算法，以解决此类具有多个分离算子的凸优化问题。主要思想是采用高斯回代过程对ADMM算法的结果进行修正，以产生一次新的迭代[15]。算法包含预测和修正两个过程，预测结果由ADMM算法产生，修正任务由高斯回代过程完成。

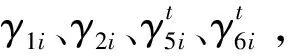
(25)

(26)

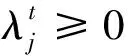
根据ADMM-GBS算法，定义非奇异下三角矩阵与正定对角矩阵如下：

其中，r1,r2,…,rN+1≥ρ。有：

是对角线为1的上三角矩阵。

对(25)进行ADMM-GBS算法的预测及修正过程如下：

3.3.1 预测

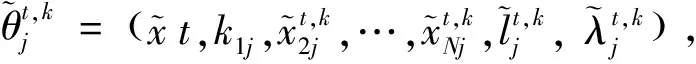
(27)

(28)

(29)

其中，对于i=1,2,…,N，有：

(30)

(31)

3.3.2 修正

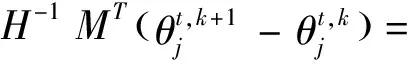
(32)

(33)

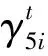
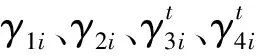
(34)

(35)

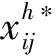
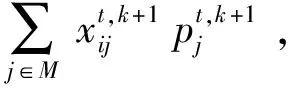
3.4 分布式算法

算法1用户侧

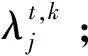
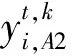
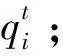
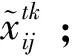
(7)根据(17)、(18)、(22)、(23)、(34)、(35)更新用户侧的协调参数；

算法2供电商侧

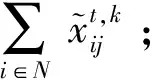
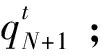
(5)将预测发电量与预测电价发送至控制中心；

算法3控制中心

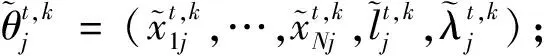
算法4在线需求响应

(1)在一天所有时隙中，对于当前及过去时隙h=1,…,t，采取实时电价计算社会福利之和；对于未来时隙h=t+1,…,T采取前一天同一时刻的对应数据代替计算社会福利之和；

(2)在时隙h=t时，用算法1～3求解下列在线需求响应问题：

s.t.(7)(8)(10)(11)(12)

(4)令h=t+1；

(5)终止条件：h>T。

对于外层目标函数多时隙社会福利模型，未来时隙变量采用前一天相应时隙相应变量值替代，遵循前文算法依次求解单时隙上子问题，进而更新最外层模型，直到更新遍历一天所有时隙，得到一天多个时隙的社会总福利值。

4 仿真模拟

将一天分为T=24个时隙，考虑系统中有M=2供电商，N=5家庭用户，每个用户配有家用蓄电池(48V，50Ah，充电效率0.8，放电效率0.8)及可再生能源发电装置(μ=0.2，σ=0.05)。用户所有必运行电器在各时段耗电量小于0.2 kwh；除用户4有1弹性电器与1半弹性电器外，其余用户均配有2弹性电器与2半弹性电器。用户电器启停的心理电价分别为[0.45,0.43,0.55,0.35,0.60]，每天总电费心理上限为[4.00,4.50,5.00,3.58,5.50]。

使用Matlab R2018b进行仿真，所得数据结果由Origin2018绘制。

如图1、2所示，迭代开始，供电商1处的电价远低于供电商2所提供的电价，用户倾向于从供电商1处购买自身大部分所需电量，以用作蓄电池充电与必运行电器使用(由于此时电价均高于用户的心理价位，用户不选择启用弹性或半弹性电器)。由图2可以看到，供电商1处的发电量迭代，在此时出现了一个高峰。随后随着供电商2处电价迅速下调，用户将部分用电需求转移至供电商2，供电商2分担了1处部分发电负担，供电商1处的发电量逐渐与用户在该处的总购电量收敛至相当水平，达到供需平衡状态。

图1 用户3购电量与供电商电价迭代

图3展示了两个供应商一天各时隙的发电情况与电价情况。通过实时电价的调控，可以有效使用户转移峰时用电至谷时，进而平滑发电端的发电曲线。结合图4、5、6、7、8可以看出，实时电价与用户的用电行为密切相关。电价低时，用户倾向于选择在此时对蓄电池进行充电，同时若电价低于心理价位，且在电器使用时段内，用户会选择在此时开启弹性电器与半弹性电器。待系统中总负载增加，电价升高，用户使用蓄电池电量应对部分电器所需，很大程度上降低了用户的购电需求，减少了供电商在用电高峰时期的发电量。由图4可以看到，用户的蓄电池与可再生能源发电，有效地承担了用户生活所需部分负载，减少了用户的购电需求，进而降低了用户购电成本。

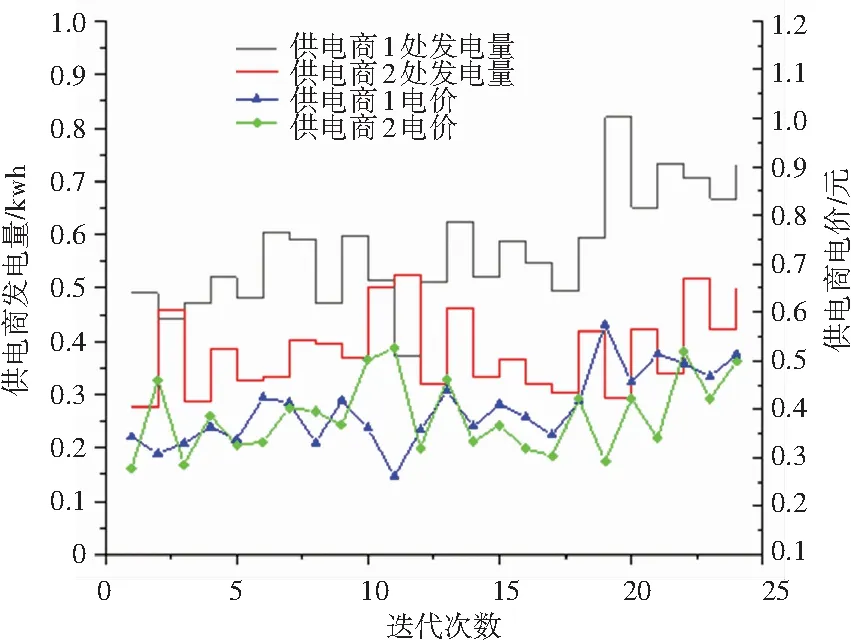
图3 供电商1一天发电量与电价

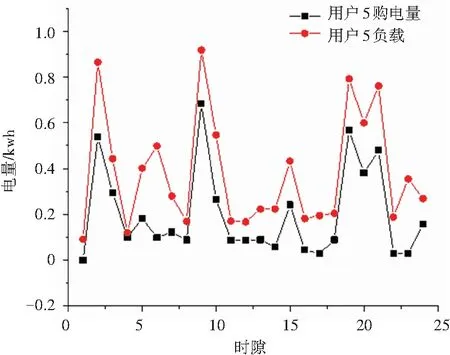
图4 用户5一天各时隙购电量与负载

表1中3种情形分别为：情形一为本文所提模型与算法；情形二为用户未配备4.80蓄电池与可再生能源装备，所有用电需求从电网购电来满足，采用本文提出的实时定价算法；情形三为不考虑用户蓄电池与可再生能源，同时采用分时定价(峰时：8:00-21:00,电价0.558 3元/kwh；谷时：21:00-次日8:00，电价0.358 3元/kwh)。分别计算这3种情形下，各用户的当日总电费，并与当日总电费上限作比较。由表1中结果可以看出：本文所提出的实时定价算法相较分时定价，能明显降低用户的当日总电费；同时当用户配备有家用蓄电池与可再生能源发电装置时，也能承担一部分家庭用电消耗，从而进一步降低用户当日从电网中购买电力所需花费。

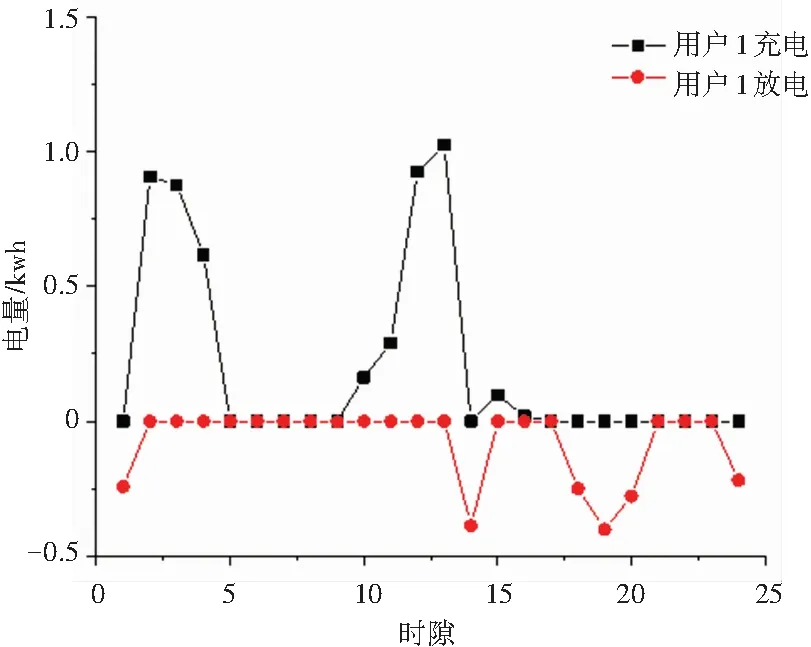
图5 用户1蓄电池充放电情况

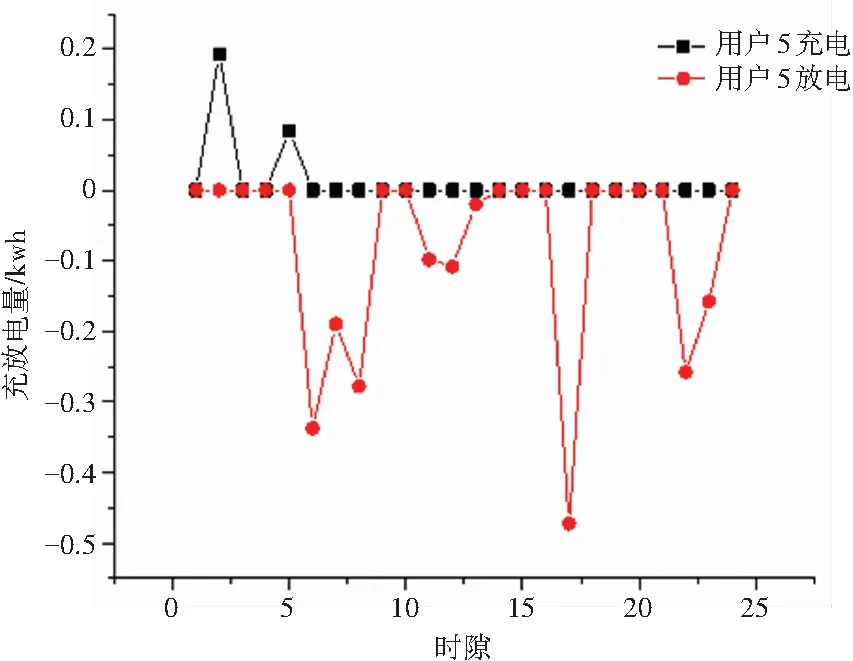
图6 用户5蓄电池充放电情况

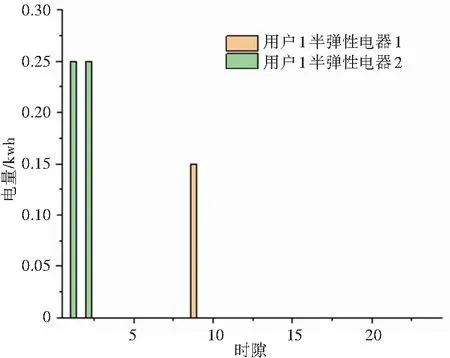
图7 用户1半弹性电器使用策略

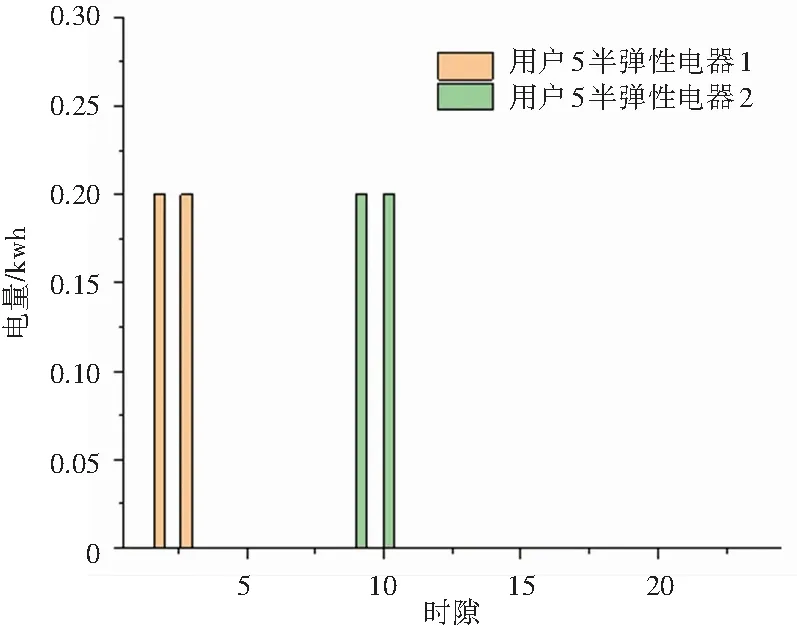
图8 用户5半弹性电器使用策略

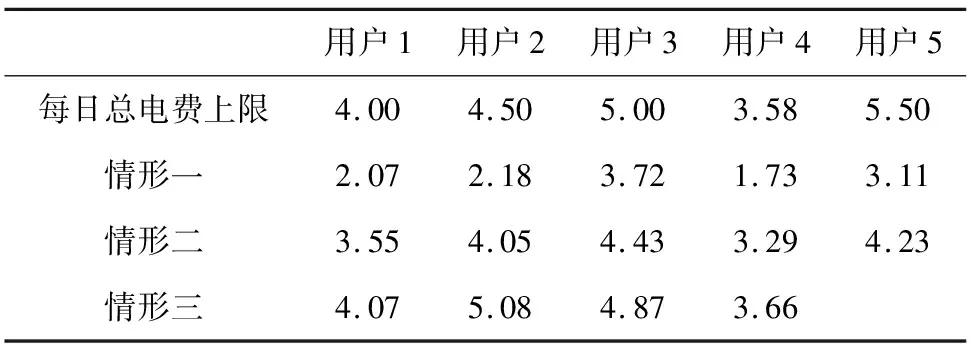
表1 3种情形下用户的当日总电费

5 结束语

本文在多供电商多用户的背景下，以社会总福利最大化为目标，建立智能电网实时定价策略模型。主要创新有：

(1)在构建模型时，将用户电器分为3类，为弹性电器与半弹性电器的启停增加用户心理价位限制；为每位用户增加当日总电费上限限制，使得模型更贴合用户日常实际用电心理与日常用电情况，有利于协助用户更合理地进行用电策略安排。

(2)针对多供电商多用户的社会福利最大化模型，提出一种基于ADMM-GBS的分布式实时定价算法，目的在于充分利用ADMM算法收敛快、且由于惩罚项的存在对目标函数可微限制温和的优点。

(3)在对时间耦合约束对应乘子迭代时，对迭代式中未来时隙的变量，选取前一天相同时段的相应变量值替代，以实现模型在线实时定价的目的。

仿真结果表明：本文所构建模型，贴合家庭用户实际用电心理与用电情况，所提算法能够有效地为用户规划实时电价用电策略，在满足用户需求的同时，减少用户购电成本。算法仅需供需双方交换少量的用电信息(所有用户在该供电商处的购电需求与供电商提供的电价信息)，避免个人及公共用电习惯等隐私的泄露。同时蓄电池与可再生能源的加入，有效改善电网系统中的资源分配，减少用户对不可再生能源的需求，降低系统中不可再生能源发电量，削峰填谷，平滑发电曲线，对节约能源、优化资源配置有所贡献。