基于代价模型的多平台分析任务流调度优化

徐超一，刘晓清，顾 淼，王 巍

(1 复旦大学 计算机科学技术学院，上海 200441；2 新浪，北京 100193)

0 引 言

数据量爆炸式增长的同时，数据分析的重要性也日益凸显。多年来，数据分析的各类需求日益旺盛，人们对数据分析的要求也不再局限于更强的数据处理能力，多个计算(分析)平台共同进行一个分析任务流的需求也随之而生。

现实中，人们经常根据数据分析需求的不同，来确定分析任务所使用的执行平台，甚至一个分析任务流中的分析算子，也可能运行在不同的计算平台上。分析任务流在不同平台之间的调度成为人们关注的一个重要问题。

RHEEM[1]是卡塔尔大学开源的跨平台数据处理系统，其支持在一个任务流中自动调用多种平台，来优化处理时间和处理性能。RHEEM借由内部的优化器，通过代价模型自动为任务流中的算子选择平台，获取最优的执行计划。Apache Beam[2]为开源的统一编程模型，用于进行跨平台的大数据分析处理。Beam是基于Google 的Dataflow Model[3]论文的一种实现。通过对数据分析的多维度规范和总结，构成了一套编程范式，实现了不同平台间的统一，但并没有关注任务流的调度问题。Kumar等人基于Actors模型[4]研发了一个带图形界面的任务流系统Amber[5]。但Amber的研究侧重于任务流执行过程中的实时调试，而不关注任务的调度顺序。而目前针对单个任务流调度的研究已经趋于成熟，HEFT[6]、CPOP[7]、PETS[8]等算法，以较高的调度效率被广泛接受。但其都需要知道每个算子的时间、资源开销以及算子间的传输开销，并且都没有考虑多平台的条件。

为此，本文研究了多平台环境下，数据分析任务流的调度和优化问题。具体研究内容包括：根据多平台的特性，提出了一种基于启发式规则优化的拓扑调度算法，来完成任务流调度；针对SQL算子加入了代价模型，能对任务流的SQL分析开销做出估计；训练了GBDT树，为用户动态选择机器学习任务的运行平台并确定开销；通过实验，验证了调度算法的优化性能和代价模型的准确率。

1 问题描述

通常来说，一个大任务可以拆分成一个子任务的集合(不同的子任务间存在一定的依赖关系)。此时，可以通过一个有向无环图DAG(Directed Acyclic Graph)的形式来表示这些关系，形成了任务的DAG模型。因此，任务流的调度问题就转化为DAG的调度问题。显然，当考虑任务调度时，首要满足的是子任务之间的依赖关系。

1.1 拓扑排序

拓扑排序，是指对一个有向无环图G进行排序。对于图中边的集合E(G)，若存在边∈E(G)，则在排序序列中，顶点u一定出现在顶点v之前。可见，拓扑排序的特性可以很好地契合子任务之间的依赖限制。通过对DAG做拓扑排序就可以得到一个满足任务流依赖关系的执行顺序。

Kahn算法[9]是进行拓扑排序的常见算法，由Kahn在1962年提出。其中心思路是：每次取出一个没有先驱节点(即入度等于0)的节点，将其放入排序序列中，然后将这个节点的所有后继节点的入度减一，重复这一过程直至排序完成。该算法的时间复杂度为O(E+V)。但需要注意的是：有效的拓扑序列并不是唯一的，每次使用Kahn算法得到的拓扑序列也不一定是一致的。

1.2 拓扑排序的局限性

如图1所示，给出的一种存在两个不同平台算子的任务流。从A算子读取输入后，分别通过后续的其它算子计算，直至结束。对于这样一个任务流，其拓扑序列显然不唯一。可能的序列有(A,B,C,D,E,F,G,H,I,J,K,L),(A,B,D,F,C,E,G,I,J,K,L,H)等等。在非常多的可能序列中，再次考虑两种比较极端的调度序列。第一种是序列L1(A,B,C,D,E,J,F,G,K,I,L,H)，第二种是序列L2(A,B,D,F,C,E,G,H,I,J,K,L)。显然，序列L1和序列L2都是满足拓扑排序的序列，但序列L1的调度效果是一个平台P1的算子和平台P2的算子交错运行。而序列L2的调度效果是优先将满足依赖的同平台算子全部调度完后，再考虑调度其他平台的算子。

图1 多平台任务流示例

对于序列L1来说，频繁的平台切换会带来额外的切换开销。更关键的是在进行平台切换的同时，需要将之前的计算结果保存，又会带来额外的内存开销。而过多的中间结果缓存会在一定程度上影响后续节点的计算速度。以Spark平台为例，过多的中间结果被缓存，会导致可用内存不足。此时，在读入当前节点数据时，需要进行GC和内存置换，从而会降低任务的处理速度。另一方面，如果一个平台内的算子操作可以连续进行，那么计算的中间结果可以用平台的内部结构表示，不仅使得整体的运算速度变快，也使整个流程的类型十分安全，可以应对复杂的计算流程，大大提高系统的鲁棒性。而例如Spark这样的平台，其原生数据结构还使得运算结果的展示具有极高的灵活性。

可以想象，当任务流的复杂度提升，或是任务流中平台数量增加，这两种调度序列所带来的开销差别是巨大的。

1.3 问题定义

朴素的拓扑排序可以解决任务流的调度问题，但在任务流的整体开销上，普通的拓扑排序是存在一定问题的。由于拓扑序列是不唯一的，对于一个给定的任务流J，使用不同的拓扑序列对其进行调度，最终整体的内存和时间开销是不同的。

因此，该问题的描述是给定一个有向无环图G(V,E)，图中节点E表示系统中不同平台的算子，图中有向边V表示算子之间的依赖关系。在满足依赖关系约束的情况下，本文希望找到一种节点序列，使得通过该顺序执行任务流时，较少的其它中间结果被缓存，且进行的平台切换最少，从而能优化整体的时间开销。

2 算法描述

针对这一问题，如果预先将所有的拓扑序列求出，再一一进行比较，选出最优解，算法的复杂度会过高。所以本文选择通过启发式规则来求解。

2.1 基于启发式规则的拓扑调度

本算法思路：先将输入节点置入结果序列，然后将其指向的节点入度减1，每次选择下一个节点(入度为0的节点)时，遵循三条规则：

(1)总是优先选择与之前节点同平台的节点；

(2)如果有多个同平台的节点，优先选择当前节点的后继节点；

(3)如果不存在同一平台的节点，则选择任意满足依赖约束的节点。算法伪代码如算法1所示。

算法1基于启发式规则优化的拓扑调度算法

输入有向无环图G=(V,E),S为入度为0的节点集合

输出调度序列L

L={}

WhileSis not empty do

//启发式规则优化

ifShas the same-platform-node with tail ofL

ifShas the successor of the tail ofL

remove the successornfromS

addntoL

else

remove the same-platform-noden’ fromS

addn’ toL

else

remove another nodekfromS

addktoL

for each node m with edge e fromntomdo

remove edgeefromG

ifmhas no other incoming edges then

insertmtoS

returnL

仍以图1为例，序列L1(A,B,C,D,E,J,F,G,K,I,L,H)和序列L2(A,B,D,F,C,E,G,I,H,J,K,L)。其中序列L2为本算法得出的调度序列。输入算子A与后继算子的切换不计入考量，L1序列总共切换了8次平台，L2序列总共切换了2次。同时可以看出，L1序列中，在计算大部分节点时，都有无关的中间结果被缓存。如在计算G节点时，节点F和节点G的结果缓存，则增加了内存和时间开销。而在L2序列中，基本保证了任务能够以一种近乎深度遍历的方式执行，减少了与当前计算无关的中间结果的缓存。

如算法1所示，本算法对图中的每个节点和每条边都会进行一次遍历。因此，本算法的复杂度为O(E+V)，其中E为图中的节点数，V为图中的边数。

2.2 代价模型

本文主要考虑的任务流算子为SQL类算子和机器学习算子，这些算子的主要运行平台是Spark和Python。因此，本文针对这两种情况分别加入相应的代价模型。

2.2.1 针对SparkSQL的代价模型

代价模型涵盖了3个基本的SQL操作：Projection、Selection和Join。

首先，系统收集一些SparkSQL相关的物理参数。参考Baldacci[10]等人的工作，系统收集的物理参数见表1。

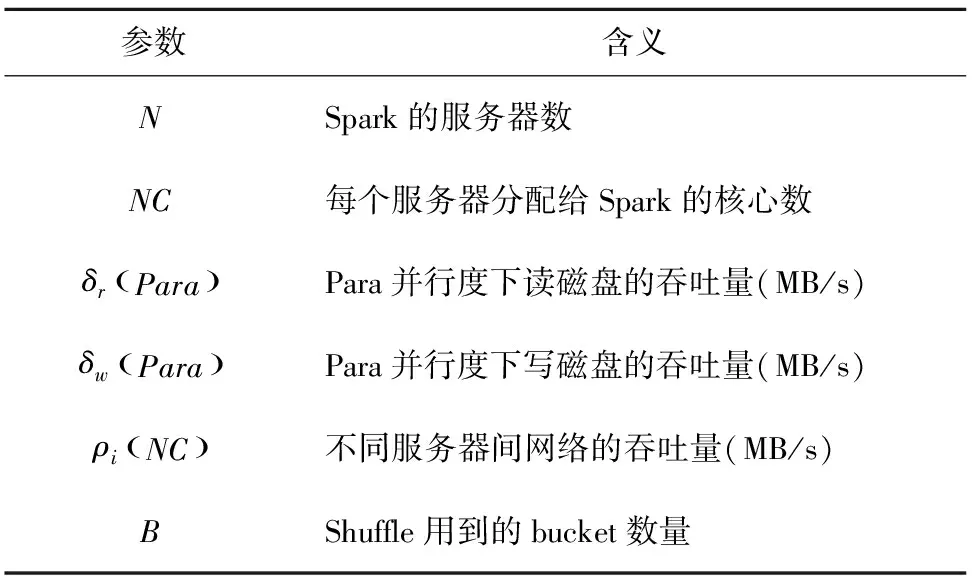
表1 物理参数收集表

根据表1可以初步得到公式(1)和公式(2)：

(1)

(2)

其中，Read(RSize)为根据读入大小得到的读入时间，Write(WSize)为根据写出大小得到的写出时间。

计算执行开销最简单的方式就是将其运行一遍，但这样就失去了代价模型的意义。事实上，代价模型不需要知道一个精确的代价，而只需要一个估计值。所以，代价模型可以对结果的数据量进行估计，再通过数据量的估算值来推断执行的代价。

在查询语句中，用户常常会使用一些过滤条件(即本文中提到的Filter操作)，在SystemR[11]中对过滤条件的估算只考虑到了数据连续且分布均匀的情况。但现实中的数据往往不是连续均匀分布的。所以考虑数据的分布情况，对数据量的估计是至关重要的。

其中，直方图是一种能够表示数据分布的统计方式。其通过分桶策略对数据做出划分，从而得到大致的分布情况。本系统选择了等深直方图来了解数据分布情况。与普通的等宽直方图不同，等深直方图尽可能的保证桶的深度相同。Piatetsky-Shapiro[12]的研究指出，等深直方图的鲁棒性更强。

直方图的构建需要有序数据。考虑到数据量增大后导致的排序开销，所以本系统使用蓄水池采样，采样后再进行排序和直方图的构建。

系统将过滤条件分为3类：单列的范围查询、单列的等值查询、多列查询。下面将分别介绍3种情况的估计方法。

(1)单列范围查询。对于单列的范围查询，可以通过等深直方图来进行估计。对于给定的一个范围查询，只需要知道其覆盖范围内的所有桶的深度即可。如果遇到桶的范围与查询范围有部分交集的情况，可以交集占桶大小的比例再做一次估算。此时，需要假设数据的分布是均匀且连续的。对于其它类型的数据，一般是将其映射成数字后再计算比例。

(2)等值查询。对于等值查询，需要知道记录出现的频率。对于一般情况下频率的计算，人们倾向于使用HashMap来统计。而当数据量非常大时，一则要求的内存非常大，二则当HashMap的冲突很高时，时间复杂度的上升，导致无法满足实时性的需要。

本系统使用了Count-Min Sketch[13]算法，其是一种可以处理等值查询的方法，可以提供很强的准确性保证。该算法的基本思路是维护一个初始为0的D×W大小的数组。对于数据中出现的每一个值，分别用D个独立的哈希函数进行映射和计数。查询频率时，依旧对其进行D次哈希，找到每一行中对应的计数值，再取其中的最小值作为估计值。

Count-Min Sketch可以看作布隆过滤器在统计方面的一个变形。其缺点是估计值总是大于等于真实值。

(3)多列查询。本系统假设不同列之间是相互独立的，只需要把不同列的过滤结果相乘即可。

综上，可以得到一个函数Filter(cols,type)。

其中,cols表示过滤的列，type表示过滤的种类。可得对Project操作的估计，如公式(3)所示：

(3)

其中，projCols表示被选中的列；all表示表中所有列；attr.Size表示该列的平均大小。

接下来可以考虑就可以完成代价模型，本文考虑3种任务。

第一种任务类型是全表扫描任务，记为SCAN。SCAN任务可以包含Filter、Project和Aggregate操作。在SparkSQL中，Filter操作和Project操作被Spark的优化器Catalyst，通过谓词下推和列值剪裁来优化执行，减小无用的元组和列对整体开销的影响。此时，数据大小的估计如公式(4)所示。

WSize=RDDSize·Project(projCols,all)

·Filter(projCols,type)

(4)

若不存在聚合操作，则整个任务可以在一个管道中边读入，边写出，整体开销如公式(5)所示。而存在聚合操作时，任务的写出必须在所有数据被读入后才能进行。此时，整体开销如公式(6)所示。

Write(WSize))

(5)

Write(WSize))

(6)

(7)

其中，TableSize为表大小，RDDSize为Spark的RDD分区大小。若不存在写出操作，Write(WSize)取0。

如果涉及Join操作，SparkSQL将根据不同情况，使用以下几种不同的Join方式：

(1)Broadcast Hash Join应用于小表(默认阈值为10 MB)和大表之间的Join。使用Broadcast的方式来完成Join操作，牺牲空间换取时间。此时，通过将小表广播到每个运行节点上，避免了Shuffle带来的大量时间开销。

(2)Shuffle Hash Join适合较小表和大表之间的Join。如果小表的大小大于10 MB，此时将小表广播出去会造成较大的数据冗余和带宽内存消耗，使得运行节点的压力较大。所以，SparkSQL转为使用Shuffle Hash join，通过Join的key将两张表进行分区，即Shuffle操作。集群内的每个工作节点都会参与Shuffle操作，每个工作节点处理每个Bucket的一部分，然后对每个分区内的记录进行Hash Join的操作。

(3)Sort Merge Join则适合两张大表之间的Join。Hash Join的方法是将其中一张表完全读入内存中，然后使用哈希的方法对另一张表进行探测和连接。而当两张表都较大的情况下，使用哈希方法对内存的压力过大。此时SparkSQL通过Join Key将两张表进行Shuffle分区，以便后续的分布式处理，然后分别对每个分区进行排序和合并。

第二种任务类型是Broadcast Join任务。该任务的开销可以用函数BJ()表示。在进行Broadcast Join时，大表仍然通过一个SCAN任务读入，而小表要进行广播，所以不需要写操作。Broadcast过程的开销，参考文献[10]的研究，得到公式(8)。

(8)

由于整个Broadcast Join是在内存中，通过Hash的方式来完成，速度非常快，瓶颈主要体现在最后写出的速度上。所以Broadcast Join的开销函数如公式(9)所示：

(9)

其中，PartitionNum为Spark中设置的分区数。

第三种任务类型是Shuffle Join。因为Shuffle Hash Join和Sort Merge Join的开销瓶颈都是Shuffle阶段，所以其开销都可以通过Shuffle Join任务来描述。该任务的开销可以用函数SJ()来表示。在进行Shuffle Join时，显然Shuffle的过程是瓶颈所在。另外，Shuffle Join只有在整个分区的数据都被读入后才能进行，不能边读边写。但是在第一阶段的Shuffle过程中，数据是一边被分配到分区，一边被读取的。Shuffle阶段的开销如公式(10)所示：

(10)

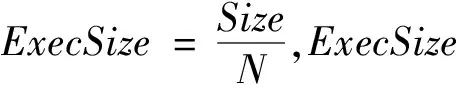
对于Shuffle Join阶段的开销如公式(11)所示：

(11)

综上所述，不同任务的开销可以通过上述3种函数的组合来计算。

2.2.2 针对机器学习任务的代价模型

由于本文考虑的机器学习任务的运行平台包括Spark和Python(Scikit-Learn)，因此会在确定运行平台后完成对机器学习任务的开销估计。

在确定了运行平台之后，就可以根据硬件信息、平台选择、任务种类(分类、聚类、回归)和训练数据的维度、数量等信息估计出这个机器学习分析算子的大致时间开销，可通过一个回归任务来完成这一开销估计。考虑到GBDT(Gradient Boosting Decision Tree)的本质是回归树，且具有很强的泛化能力，因此本文使用GBDT回归树来完成对机器学习算子时间开销的估计。

3 实验结果与分析

本文在 Spark 集群上进行实验，其中包括 1 个 master 节点和 2 个 worker 节点。节点的硬件配置如下: Intel(R)Xeon(R)Silver 4208@2.10 GHz,24核；64 GB 内存；8 TB硬盘。软件配置为:Linux Ubuntu 18.04、Spark-2.3.1、Python 3.6.8版本。

用于数据分析流程的训练数据为Numpy随机生成。而用于文本分析流程的数据，来源于新浪公司CMS内容管理系统真实发布的新闻文章(为2019.01.01～2019.04.22发布在新浪新闻娱乐频道的所有新闻文章)，去重后共有2 172 925篇。实验时先根据关键词筛选出1 000篇文章进行训练。

第一组实验：测试调度算法的优化对系统性能的影响。

实验比较了朴素拓扑调度和基于启发式规则优化的拓扑调度在任务流调度中的开销差异。

本文首先通过Numpy生成了12 GB的训练数据，并限制系统内存为10 GB，模拟复杂任务下的情况，并使用多种不同的算子组合构成任务流，进行实验。其中一种任务流如图2所示。实验结果见表2。

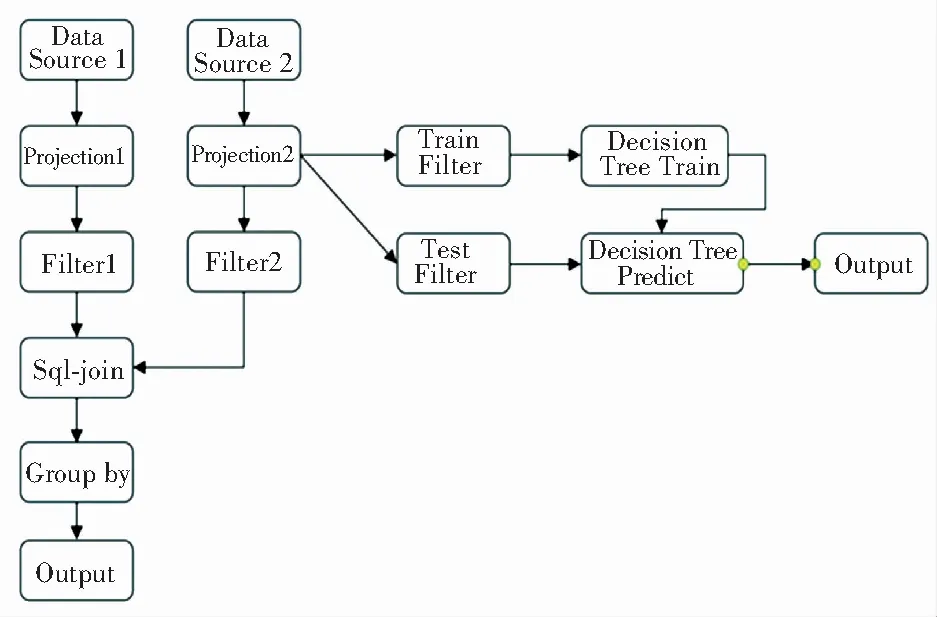
图2 实验任务流示例

表2 调度性能测试

第二组实验：测试代价模型的准确率。

本文在TPC-H的标准下，生成了12 GB的表数据。分别测试了不含Join操作的简单SQL和包含了Broadcast Join或Shuffle Join操作的稍复杂SQL的实际执行时间，并将之与代价模型给出的预估时间进行对比。实验结果见表3。

表3 代价模型准确性测试

误差率的定义如公式(12)所示：

(12)

由表3中可以看出，Join操作带来的复杂性提升，使得不含Join的简单SQL的估计更加准确，对带Join的SQL的开销估计则稍微有所下降。而在两种Join类型之间，由于Shuffle Join涉及两张表的分桶和更多的数据传输，其过程更加复杂，使得这种类型下的平均误差率最高，达到了33%。但3种情况下，代价模型的误差控制在35%以内，达到了预期。

4 结束语

针对多平台条件的任务调度问题，本文提出了基于启发式规则优化的拓扑调度算法，并且结合代价模型完成了对SparkSQL任务和机器学习任务的开销估计。通过实验证明了调度算法的有效性。在后续工作中，可以结合历史运行数据，通过一个端到端的机器学习模型完善和改进系统的代价模型。