基于时频分析和卷积神经网络的微地震事件检测
盛 立, 徐西龙, 王维波, 高 明
(中国石油大学(华东)控制科学与工程学院,山东青岛 266580)
水力压裂是非常规油气资源勘探开发领域的一项重要技术[1-3]。水力压裂过程中大量的高压流体被注入目标储层,导致地层岩石破裂,产生微地震事件[4]。通过处理分析微地震事件监测数据,可以解释压裂区域和裂缝发育方向等信息,进而评价压裂效果[5]。微地震事件检测的目的是剔除噪声干扰信号,因此快速、准确地检测微地震事件是后期数据处理的基础。面对海量的微地震监测数据,人工识别微地震事件的方法难以满足实际需求[6],而常规方法处理微地震数据的有效性依赖特征提取类型和阈值设定,如何建立高效的微地震数据分析模型,是解决事件检测问题的新思路。近几年,卷积神经网络(CNN)凭借权重共享和稀疏连接的特性在语音识别、自然语言处理等领域广泛应用[7-8]。最近,卷积神经网络作为特征提取工具被用于地震数据处理领域中。Ross等[9]建立卷积神经网络分类器实现南加州地区地震事件的震相和噪声识别。张国印等[10]将卷积神经网络与频谱分解结合挖掘地震数据信息进行岩性储层预测。冯其红等[11]用卷积神经网络建立对抗神经网络框架预测气窜方向。笔者利用时频分析方法能够有效体现微地震信号时频域综合信息的优势,利用S变换对微地震时域信号进行处理,建立时频谱样本数据集,建立深度卷积神经网络进行训练测试,实现时频谱中抽象特征的自动提取。同时,考虑阵列式地面微地震监测的特性,提出根据波形相关性综合模型的分类结果判别微地震事件。
1 原理介绍
1.1 S变换
微地震监测数据大都属于非平稳信号,而时频分析方法在处理非平稳信号时具有独特的优势。S变换是由Stockwell等[12]提出的一种时频分析方法,克服了一般方法中窗函数固定不变的问题,可以反映信号真正的时间频率谱,完整地描述信号特征[13]。考虑到S变换优越的时频特性,利用该方法对微震数据进行二维时频谱提取,经S变换后得到的时频谱定义如下:
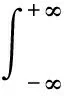
(1)
(2)
式中,x(t)为待转换信号;w(τ-t,f)为高斯窗口;t为时间;f为频率;τ为控制高斯窗口在t轴位置的时移参数。
1.2 卷积神经网络
卷积神经网络是一种具有深度结构的前馈神经网络,其网络特性显著降低了模型的复杂度,减少了训练参数的数量[14-15]。典型的卷积神经网络通常由卷积层、池化层、全连接层和输出层组成。
卷积神经网络可以处理不同维度的输入信号,其中卷积层通过使用卷积核遍历输入信号,对输入的局部区域进行卷积运算[16],计算公式为
(3)

池化层在卷积层之后,通过下采样压缩输入的数据矩阵。经过多个卷积层和池化层的交替叠加,全连接层将提取特征进行非线性组合,之后传递给依据任务设定的输出层。训练过程中,卷积神经网络采用梯度下降算法最小化损失函数,以更新模型参数。本文中损失函数根据标签向量与模型预测的概率向量构造,使用的是softmax交叉熵,定义为
(4)

2 事件检测模型构建
2.1 数据集构建
本文中数据主要来自于川渝地区LG172油井水力压裂地面微地震监测数据,这是一口常规储层直井。观测数据通过高灵敏度检波器(采样频率1 000 Hz)采集所得,均使用垂直分量波形。由于有效微地震事件信号在整个监测波形数据中占据比例非常小,直接使用会导致正负样本分布不均匀,使得神经网络无法有效学习。因此截取有效波动在内的1 000个数据点(采样时间1 s)为预备正样本,只含背景噪声的数据为预备负样本。
原始微地震监测数据均为时域波形信号,并不包含频域信息,直接输入网络可能影响模型的识别精度。因此需要对预备样本进行时频变换,以充分展现信号的时频特征。经过S变换处理,一段时域信号的时频谱正/负样本如图1所示。将正/负样本标注为1/0,为了使交叉熵损失函数计算更为合理,使用One-Hot编码。样本类型1和0编码分别为01和10。
本文中数据集共包括40个微地震事件,共有950条微地震事件监测波形数据。经过上述处理后,得到含微震事件的时频图样本850个,含背景噪声的时频图样本900个。其中随机抽取1 225个样本作为训练集,525个样本作为测试集。
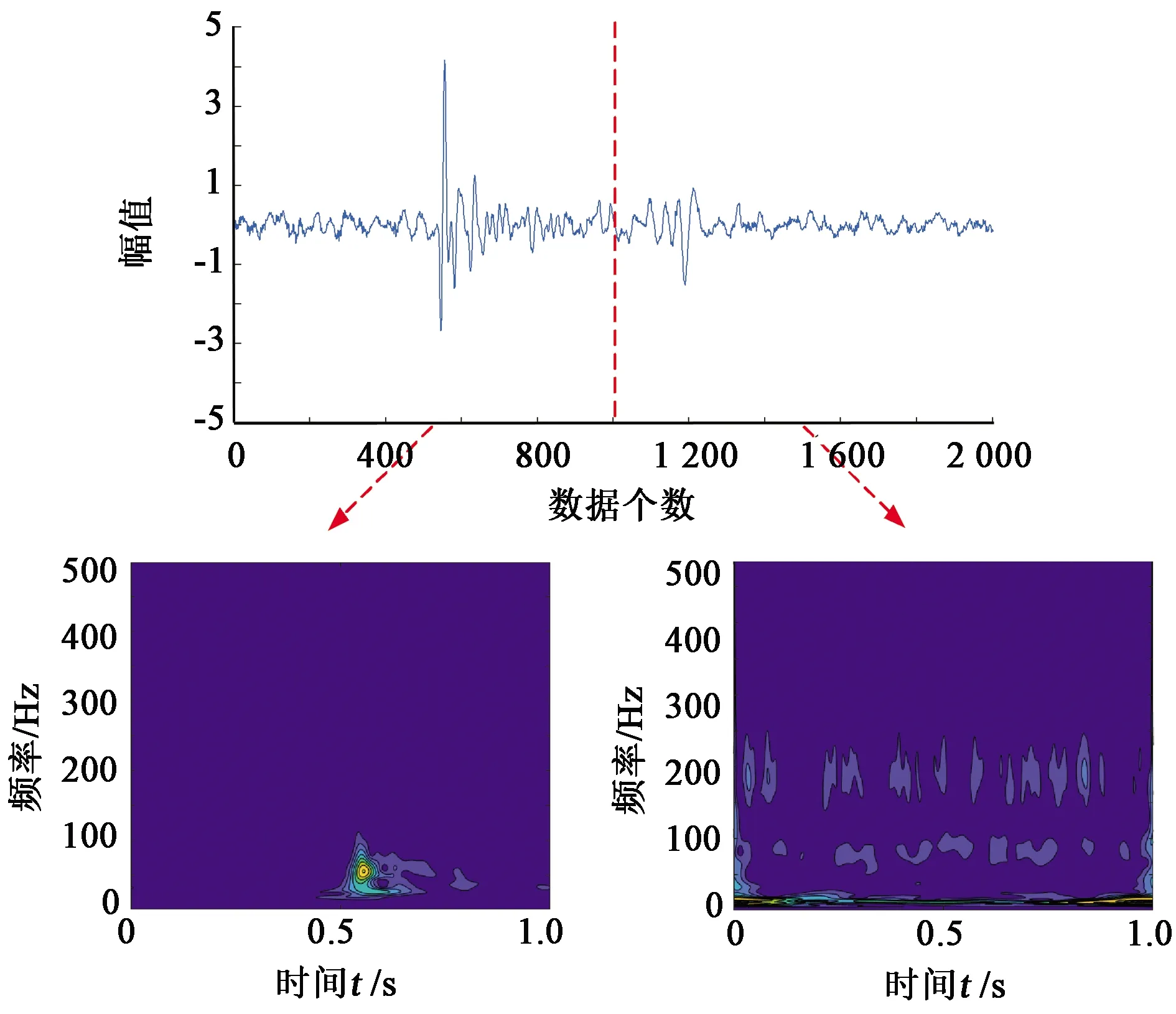
图1 时频谱正/负样本Fig.1 Positive/negative samples of spectrum
2.2 深度卷积神经网络模型构建
建立如图2所示的深度卷积神经网络模型,其中,输入数据具体形式为RGB格式的时频谱样本,可用 100×100×3的张量表示。本文中将网络输入通道设为3,因此可用二维卷积处理。图中C2层为利用32个大小为5×5×3、步长为1的卷积核和2×2的池化区域对输入图像进行处理后的特征映射,C3层、C4层、C5层、C6层分别使用64、128、256、512个5×5×32、3×3×64、3×3×128、3×3×256卷积核以相同步长和相同大小池化区域对前一层的特征映射进行处理,经过10个交替排列的卷积层和池化层提取特征后,输入至C7、C8全连接层进行特征一维化处理,最后采用softmax分类器作为网络的输出层,将抽象特征输出为对应原始时频谱样本所属分类的概率值,从而完成样本分类。
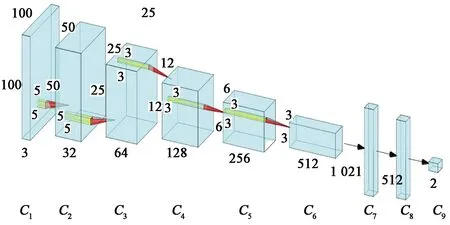
图2 深度卷积神经网络模型Fig.2 Model of deep convolutional neural network
2.3 相关性分析
水力压裂过程中微地震事件发生时,通常会触发多个地面监测站点的检波器采集波形数据,因此监测数据存在有效信号被多站点接收且到时接近的波形相关性。对于由背景强噪声造成的低信噪比信号,利用单一站点的监测波形数据来判别是否存在微地震事件容易误判。因此可以利用卷积神经网络对各站点监测数据进行检测,在此基础上根据波形相关性进行微地震事件的自动识别。同一事件各站点待检测数据样本可能被卷积神经网络分类识别为包含有效信号,也可能被识别为背景噪声,在此基础上若有一定比例(该比例可根据实际信号质量情况而定)以上的站点被分类识别为包含有效信号,则可确定为微地震事件,否则为背景噪声。
2.4 微地震事件检测流程
基于时频分析和卷积神经网络的微地震事件检测方法主要分为数据处理、模型训练和事件检测3部分。如图3所示,原始数据经过时频变换等一系列预处理操作后分为训练集和测试集。将训练集样本导入卷积神经网络模型进行训练,训练完成后将测试集样本输入到网络中进行模型性能评估。由于训练集样本和测试集样本没有重复,因此可以模拟模型实际部署之后的情况。如果模型性能良好,则保存模型参数。事件检测时将待检测数据经过类似预处理后按批输入至保存的模型中,然后对模型输出各站点数据检测结果进行相关性分析,从而实现微地震事件的判别。

图3 微地震事件检测流程Fig.3 Flow chart of microseismic event detection
3 深度卷积神经网络模型训练
实验在深度学习框架Tensorflow上进行,计算机基本配置为CPU Intel Core i5-7400处理器、3.0 GHz主频和8 GB运行内存。训练过程采用ADAM优化算法,学习率为0.001,同时为了抑制过拟合加入Dropout调整策略。在训练过程中,卷积层层数以及卷积核的数目和尺寸、池化层层数和尺寸、失活率和迭代输入批次等结构参数都不同程度影响模型的检测结果。因此为了优化模型结构,以提高模型对事件的识别性能,本文中考虑准确率和训练时间两个指标,选取卷积层层数、池化区域、输入批次和失活率4个关键参数,进行多次实验对比,结果见图4。

图4 模型参数选取Fig.4 Selection of model parameters
可以看出,不同参数的选取对于模型的训练结果有较大影响。通过分析对比,确定了4个参数的较优值,分别选取卷积层数为13、池化区域为2×2、输入批次为30、失活率为0.5,其余参数凭经验设定。在确定模型的基本结构后,分别将卷积神经网络结合S变换(CNN+ST)与直接输入时域信号(CNN),卷积神经网络结合短时傅里叶变换(CNN+STFT),卷积神经网络结合小波变换(CNN+CWT)等方法进行对比。通过选取不同形式的数据集输入至同一模型中,分别为时域信号(1 750段),经短时傅里叶变换后的时频谱,经连续小波变换后的时频谱,经S变换后的时频谱(各1 750张)。
将不同数据集输入模型中,在输入样本的过程中引入小批量mini-batch(训练设置为30个样本)来加快网络训练速度。每次训练输入一个小批次样本,循环训练所有批次,将所有数据遍历一遍称为一个迭代周期。经过50个迭代周期(约2 000步迭代),各方法测试集准确率如图5所示,各方法在不同迭代周期数值下的测试集损失函数值如图6所示,各方法训练所需时间以及识别单个样本所需时间如表1所示。

图5 4种方法的准确率Fig.5 Accuracy of four methods
由图5可以看出,CNN方法的效果不理想,测试集准确率仅约为76.4%,这可能是由于数据集中包括许多低信噪比微地震事件,仅凭时域信息难以判别所致;CNN+STFT方法的效果有明显改观,测试集准确率最后稳定在约93%;CNN+CWT的效果较好,测试集准确率约为96%;CNN+ST的效果最好,测试集准确率最终约收敛于99%。可见将时域信号经过处理转换为时频谱后的检测结果要普遍优于直接输入时域信号。这说明相比于时域信号,时频表达更能表现数据的变化特征,其中以S变换后得到的时频谱为数据集效果最佳。
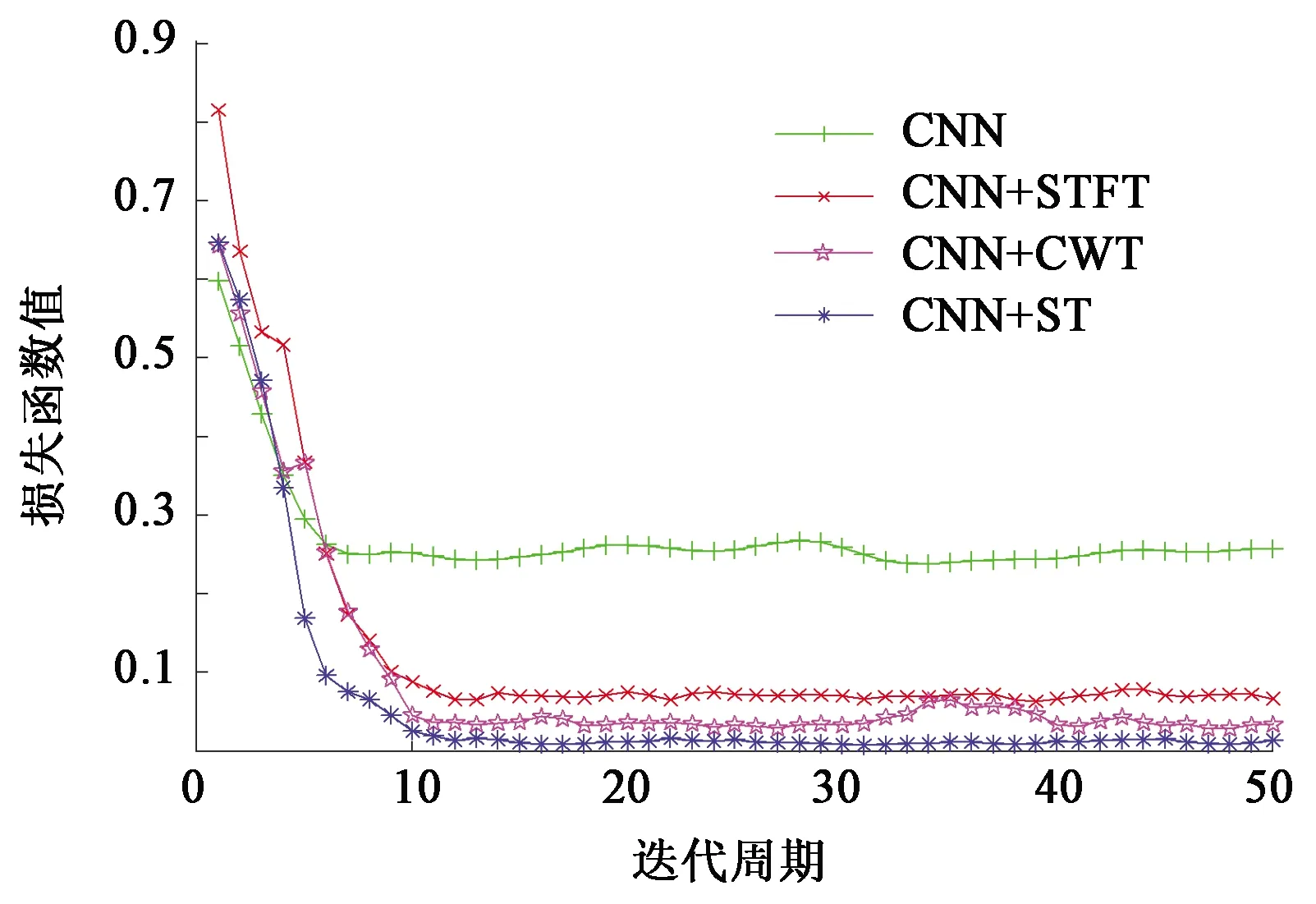
图6 4种方法的损失函数Fig.6 Loss functions of four methods
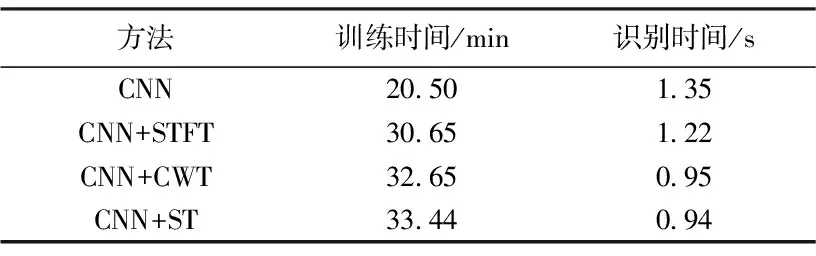
表1 4种方法的时间效率
由图6可以看出,随着迭代周期的增加,各方法的测试集损失函数值不断下降,最终趋于稳定。其中CNN方法的收敛速度最快,在迭代周期为7时损失函数值就趋于稳定,但相比于其他方法,损失函数值明显较大。其余时频特征图结合卷积的方法收敛速度几乎相同,均在迭代周期为13时才趋于稳定。其中CNN+ST方法的损失函数值明显小于其他方法。由表1可以看出,4种方法在训练时间上存在一定差异,其中以CNN+ST方法训练耗费时间最长,而CNN+CWT和CNN+STFT训练时间略小,但都明显大于CNN方法训练时间。这是由于时频谱较时域信号包含信息更丰富,而且分辨率越高的时频谱包含信息越详细,导致模型提取特征耗费时间越久,收敛速度越慢。不过在模型训练完成以后,各种方法对单个样本识别时间差距不大,时频分析与卷积神经网络组合的方法识别速度甚至更快。
为了降低随机因素的影响,每组实验重复5次,4种方法的比较结果如图7所示。
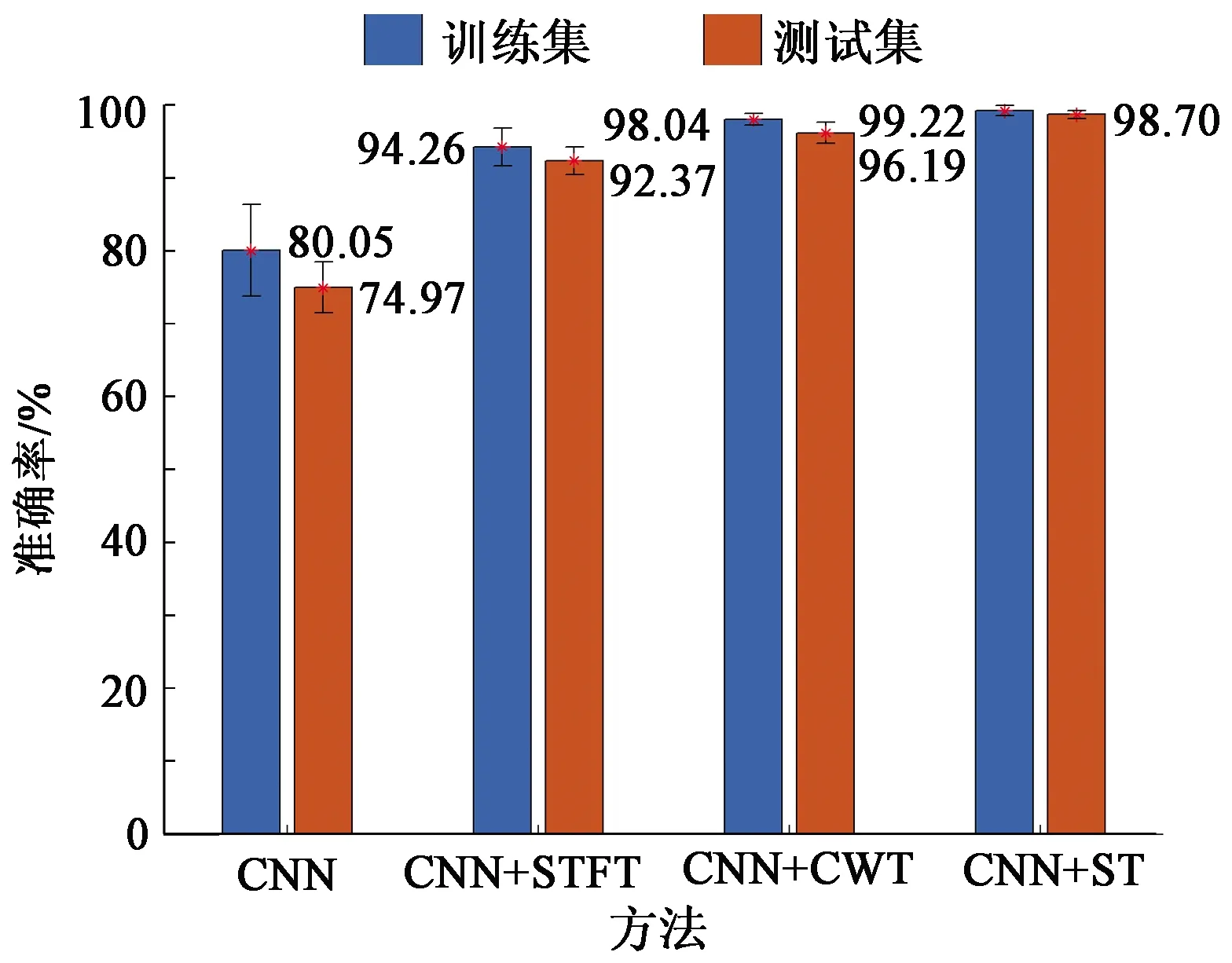
图7 重复实验下4种方法的准确率Fig.7 Accuracy of four methods under repeated experiments
由图7可以看出,无论是训练集或测试集,CNN、CNN+STFT、CNN+CWT和CNN+ST方法所得到的平均准确率都是递增的,与图5分析类似。其中CNN+ST方法的平均测试准确率比效果最差的CNN方法和效果较好的CNN+CWT方法分别高23.73%和2.51%。同时,CNN+ST方法的训练集和测试集标准差明显较小,这意味着该方法具有较高的稳定性。
综上,CNN方法具有较快的收敛速度和训练时间,但是其正确识别率及识别性能稳定性较差。这是由于时域信号包含变化信息较少,特征提取不充分。相比之下,由于时频谱包含时频域的综合信息,具有更加丰富的变化特征,所以CNN+STFT、CNN+CWT、CNN+ST的方法收敛较慢,训练时间长,但是也具有更好的识别准确率和识别稳定性。在3种卷积神经网络结合时频谱方法中,CNN+ST方法最佳,不仅具有较优的收敛速度,较高检测效率和准确率,而且识别性能稳定性更好,因此选用该方法。
4 应用结果
分别对微地震合成信号和实际的微地震监测数据进行事件检测。其中模拟微地震的合成信号是通过假设LG172井某个震源点发生破裂释放地震波,根据理论时差合成。实际数据则选用模型训练中未使用的LG172井部分时刻的典型监测数据。
4.1 检测低信噪比事件可行性分析
为了测试S变换应用于低信噪比信号的有效性,分别对低信噪比的合成信号和实际监测信号进行时频变换。选用一段初至清晰的微地震监测数据为初始信号,在此基础上叠加高斯白噪声,得到低信噪比的合成信号,之后对初始信号和低信噪比合成信号进行S变换,得到时频谱如图8所示。同时选取一段水力压裂过程中的微地震监测数据(图9(a))进行变换,得到时频谱(图9(b))。
由图8可以看出,对于信噪比较高的初始信号,无论是时域信号还是时频谱,对于有效信号(波动部分)均有很高的辨识度,而对于图8(c)中叠加噪声的合成信号,其信号质量较差,有效信号几乎被噪声淹没。对于经过S变换得到的时频谱,虽然噪声污染严重,但是有效信号的局部特征清晰,仍可确定该信号包含微地震事件。由图9(a)可以看出,该段低信噪比数据有效信号部分(图中标识处)几乎被淹没在噪声中,较难观察。但是在经S变换后的时频谱中局部特征明显,时域信息和频域信息均能显著反映。综上,相比于时域信号,低信噪比信号的有效信号部分在时频谱中具有更高的可辨识度,因此利用卷积神经网络提取时频谱的抽象特征以检测低信噪比微地震事件具有可行性。
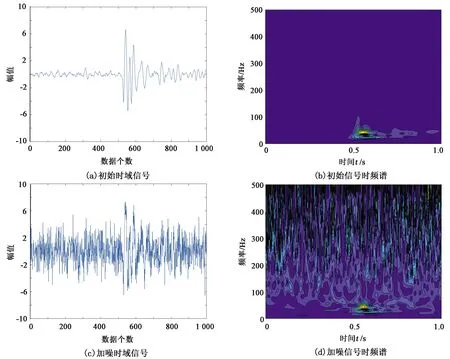
图8 低信噪比合成信号可区分度对比Fig.8 Comparison of distinguish ability of synthetic signals with low signal-to-noise ratio
4.2 合成数据检测结果
地面微地震监测系统应用于实际压裂过程中时,数据采集一般是埋设在地表浅层土壤的检波器阵列完成的,不可避免地受到各种干扰的影响。为了便于量化分析,使用合成数据测试模型的抗噪能力。合成数据通过假设某震源点,叠加雷克子波和高斯随机噪声生成。图10为信噪比为-6 dB和-12 dB时的合成信号,每个模拟站点的监测数据长度为3 s,图中截取了20个站点显示。可以看出,信噪比为-6 dB时合成信号初至较清晰,一些局部位置被噪声掩盖,但通过有效信号的同相轴连续性仍可辨认出微震事件,而当波形数据信噪比为-12 dB时,由于噪声污染严重,几乎所有的有效信号都被淹没在噪声中。对于这样的低信噪比微震数据,几乎无法在时域采用人工方式或常规自动识别方法判别微震事件是否存在。

图9 低信噪比实际监测信号可区分度对比Fig.9 Comparison of distinguish ability of actual monitoring signals with low signal-to-noise
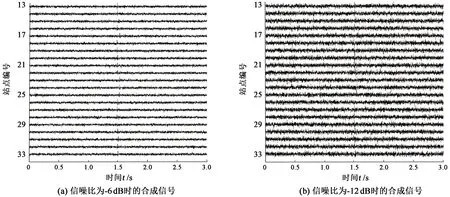
图10 不同信噪比的合成信号Fig.10 Composite signals with different sigal-to-noise ratios
合成信号中8个站点的检测结果如图11中红线标识所示(在图中表示为1~8道),其中高位值表示检测到了有效信号样本,为便于观察,图中只截取包含有效信号在内的3 000个数据点显示(在模型训练中为3个样本)。当波形数据信噪比为-6 dB时,8个站点均在1 000~2 000数据点处(第2个样本)检测到了有效事件信号(图11(a)),且没有出现误判情况。当波形数据降至-12 dB时,8个站点中有7个站点在1 000~2 000数据点处检测到了有效事件信号(图11(b)),但是在第4道的0~1 000数据点(第1个样本)处以及第6道的0~1 000数据点(第1个样本)处均出现了背景噪声样本被误判为包含有效信号样本的情况,同时在第6道处1 000~2 000数据点(第2个样本)被误判为背景噪声样本。考虑到地面微地震监测系统各站点监测数据的相关性,这些被误判的样本只被个别的监测站点包含,因此并不影响微地震事件的判别。图11中绿线标识为使用CNN方法进行检测的结果,可以看出,对于-6 dB和-12 dB的合成信号,各道数据均出现大量的样本误判情况,若在此基础上考虑各站点监测数据的相关性,易造成微地震事件的误判。

图11 合成信号部分站点监测波形数据检测结果Fig.11 Detection results of waveform data monitored at some stations of synthetic signals
4.3 实际监测数据检测结果
油气井压裂地面微地震监测信号的差异很大,这些差异主要由微地震事件对应的震源破裂规模和破裂尺度所决定。另外,由于监测站点距离井的距离、压裂设备震动强度不同,微地震波形数据受到的干扰程度也是不同的。图12为4种典型的地面站点监测数据,每个站点监测数据长度为10 s。可以看出,图12(a)为一个33站点的微地震事件,其波形数据信噪比较高,信号明显;图12(b)显示的微地震事件虽然几乎没有噪声干扰,但是其信号微弱;图12(c)中的微地震波形数据噪声污染严重,信噪比较低;图12(d)为夜间安静环境下的背景信号。

图12 LG172井地面监测站点波形数据Fig.12 Waveform data of surface monitoring station of well LG172
利用CNN方法和CNN+ST方法对上述实际监测数据进行微地震事件检测,部分站点的检测结果如图13所示,其中红绿线标识意义同合成信号检测结果。为便于显示,图中只截取包含有效信号波动在内的3 000个数据点。由图13可以看出,对于信噪比较高的微地震事件(图13(a)),CNN方法和CNN+ST方法检测效果都很好,8个站点均能检测到有效信号。对于微弱微地震事件(图13(b)),CNN方法出现了多个站点未检测到有效信号的情况,CNN+ST方法也出现了个别站点未能成功检测的情况,这可能由于部分地面监测站点所采集到的微地震波形太微弱,如第2道站点数据,其有效信号波动几乎不存在。对于低信噪比微地震事件(图13(c)),CNN方法在第1、2、6、7和8道数据均出现多个样本误判,而CNN+ST方法也存在将个别背景噪声样本误判为有效信号的情况,如第2道数据中2 000~3 000数据点(第3个样本)。但从第1道与第2道数据检测中可以看出,所提方法均能检测到几乎被噪声淹没的有效信号。对于背景噪声(图13(d)),CNN方法在第1道1 000~2 000数据点处出现样本误判情况,而CNN+ST方法在8个站点均未检测到有效事件信号,且没有出现样本的误判情况。
以上分别对低信噪比的合成信号和实际微地震监测数据进行事件检测,检测结果表明CNN方法在检测低信噪比事件和微弱事件时存在一定的局限性,而CNN+ST方法在各种情形下均能有效判别微地震事件,尽管出现部分样本误判情况,但在后续统计各站点波形分类结果时可根据地面微地震监测数据的相关性排除误判干扰,因此不会对微地震事件判别造成影响。
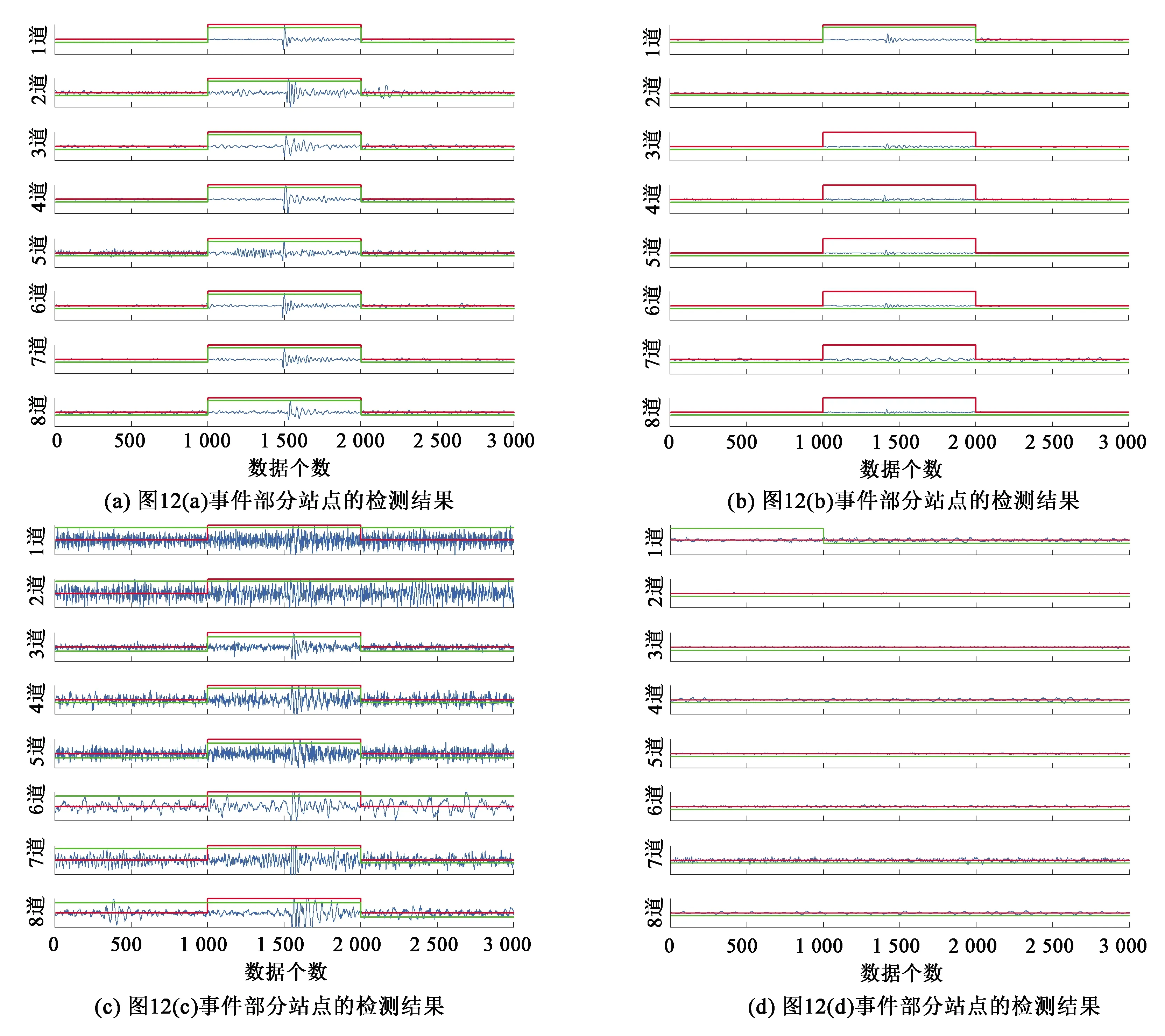
图13 LG172井监测信号部分站点的检测结果Fig.13 Detection results of monitoring signal stations in well LG172
5 结束语
利用时频分析方法中的S变换处理原始数据,建立时频谱样本数据集,通过对建立的深度卷积神经网络模型进行训练和测试,实现样本的特征提取和分类识别。相比于传统的识别方法,所提方法无需根据特定条件设定阈值,在模型训练过程中可实现特征的自动提取。通过对低信噪比的合成信号以及LG172井的典型监测数据进行事件检测,证明了所提方法具有较好的应用效果。此外,单个卷积神经网络模型不可能对于所有地区、所有类型井的监测数据的检测都有效,在后续研究中将通过改进S变换,扩展数据集容量等方法来提高模型的识别精度和应用范围。

