基于AHP-改进的模糊综合评判模型的应用
张仙凤
(朔州师范高等专科学校,朔州 036002)
在实际的销售决策中发现,传统的模糊综合评价操作比较复杂,本文基于语言分布评估,对原来的模糊综合评价进行了一些改进。改进的模糊综合评判模型,数学理论简洁却又不失完善,方法本身简单易用,能够将复杂问题简单化,最重要的是其评估结果能够与实际相匹配。
一、微信化妆品购物评价指标体系
现在的购物方式多种多样,我们可以数出很多种,如实体店购物、网上购物、电视购物等,但自从微信走进我们的生活,微信成了我们日常交流、沟通最重要的方式。哪里有人哪里就有商机,微信销售者越来越多,微信购物者也越来越多,而研究微信中消费者购物决策也成为我们常常思考的问题。
在微信平台中,购物者一般通过微商C1、微商城C2、微店C3等渠道进行微信购物,并且考虑使用效果c11、价格满意度c12、服务优劣c13等。分析这些情况构建二级评价指标体系,如图1所示。

图1 评价指标体系示意图
下面就各指标进行描述:
(一)使用效果
消费者购买化妆品,首先考虑的就是化妆品的使用效果。而对于已经体验过产品的客户来说,她们最有发言权。通过用户亲自体验产品,并将使用效果分享,以用户评价的形式对其他客户产生良好影响。
(二)价格满意度
购物者对于产品而言,并不是光考虑使用效果这单一因素的,购物者会根据自己的实际情况对价格进行考虑,并会对比不同牌子的价格,选择适合自己的品牌。由于消费水平的提高,各种消费渠道的冲击,同时现代女性更自立,购物更精打细算,价格也是购物者考虑的一个重要的指标。
(三)服务能力
服务能力包括客服的态度、沟通能力以及售后的优劣。其实,消费者有时对于自己的状况不是很了解,希望销售者或者客服能给予辨别及专业的解答,并针对自身情况给出合适的建议,所以服务对于成交来说是非常关键的。
(四)广告力度
(五)质检公开度
现在微信品牌越来越多,给人们带来极大便利的同时带来了更多选择机会,当然其中不乏鱼目混珠者。而对于好坏、优劣的辨别就变得比较困难,此时经过质监部门检测,并有检测合格证的品牌是非常有说服力的。
二、指标因素权重的确定
指标因素权重的确定是最关键的。在本文中,将调研整合的实验数据进行分析计算,确定了群组综合权值。与此同时,采用判断矩阵分析法,进而确定关联因素的比重数值,最后将得到判断矩阵。根据建立的检验模型,对其一致性进行了严格的检查验算。具体步骤如下:
第一步:构造判断矩阵(见表1)。选取S位从事微信销售的专家组,这S位专家从事微信销售时间较长,她们的评判能基本反映微信产品消费的趋势和特点。专家们对二级评价因素做了两两比较,并在此基础上,对一级评价因素做了两两比较,即可得判断矩阵C=(cij)n×n。

表1 判断矩阵标度及意义
设有n个因素集合C={C1,C2,...,Cn},现在从集合中取两个子因素Ci,Cj(i,j=1,2,…,n),Cij表示xi和xj对C的权重之比,这样我们得到n×n个数值,从而构建出矩阵C=(cij)n×n,C被叫作判断矩阵,其特点为:若xi与xj对C比较为cij,则xj与xi对C的权重比为:
第二步:计算各指标的权重值。
对C=(cij)n×n,按以下方法计算权重值。
综上所述,丝绸之路青海道在5至7世纪发挥了沟通中西方交通的重要作用,使中外交通贸易并没有在哪个大动荡时期而中断;积极联络塞北与江南、南朝与北朝的政治往来,为以后隋唐一统局面奠定了地缘基础;佛教在本土的落地生根和扩布,又为藏传佛教的再度复兴创造了丰厚的土壤条件。与此同时,青海的社会在经济、文化方面有了进步,虽然远离中原政治文化中心,但始终保持了对中原文明的强烈认同。结合文献,从出土文物重温这段历史,对于建设家园、开发青海,无不有启示与裨益。
(1)将C=(cij)n×n中一行中元素相乘,并标记为Pi。

(2)求Pi的n次方根Dni。

(3)权重计算。对向量Dni进行归一化,得到其权重值。

(4)一致性检验。偏差一致性指标CI。
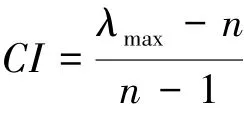
式中:λmax是矩阵的最大特征根。


式中:RI为平均随机一致性指标,随机一致性比率CR,CR=CI/RI,见表2。CR<0.1时,经判断这类矩阵是可取的,否则若不符合条件,这类矩阵就是不可取的,建议进行修正。

表2 RI值表格
第三步:确定群组综合权值。
对于S个专家的判断矩阵,我们可分别得出它们的排序向量ωk=(ω1k,ω2k,…,ωnk)T,k=1,2,…,s则ω=(ω1,ω2,…,ωn)T。用下式求出(j=1,2,…,n),式中是专家重要性的量化表示。将各位专家在微信销售从事的时间为依据,销售时间长的权值比重就要设置大点。若第k位专家在微信中销售时长为Ek年,则她的权值比重数就定为:,其中
系统权重确定后,就可以进行决策了。权重数值若比较大,则说明其对应的参考因素影响力就大。
三、微信购物中化妆品的模糊综合评判模型
根据以上得到各因素的权重,下面将结合改进的模糊综合评价法和语言分布评估群决策法对方案进行评价。具体步骤如下:
(一)建立消费者集和评价术语集。
选取在微信中购买化妆品的t组购物者ds(s=1,2,…,t),确定ds的权重,构成权重向量v=(v1,v2,…,vt)。例如,可以选取四组消费者分别为20岁以下、20—30岁、30—40岁和40岁以上的女性消费者,她们的权重可以通过其微信购物的数量确定。
消费者采用评价语言术语集S={s-2:很差,s-1:差,s0:一般,s1:好,s2:很好},对于一级评判因素,这些是会影响购物者微信购买化妆品的因素,下面将对其进行评价。
(二)对各购物者进行问卷考察,得到语言分布评估决策矩阵。
在二级因素Cj(j=1,2,3,4)下,通过调查问卷的方式,让各组消费者给出选取的化妆品(评价方案),记为xi(i=1,2,…,r),在各一级因素cj1,cj2,cj3,cj4,cj5下的评价。由此可以得到各方案在cj1,cj2,cj3,cj4,cj5下的语言分布评估评价值。构造ds组消费者的语言分布评估矩阵
(三)对Ms(s=1,2,…,t)进行集成,得各二级因素Cj(j=1,2,3,4)下的评价值。具体步骤:
设有三(二)中的二级因素Cj下一级因素cj1,cj2,cj3,cj4,cj5的权重向量ω=(ω1,ω2,…,ω5)。
第一步,利用DAWA算子将消费组ds的语言分布评估矩阵Ms(s=1,2,…,t)进行集成得到决策者ds对方案xi的评估值
第二步,利用DAWA算子对每组消费者ds(s=1,2,…,t)对方案xi(i=1,2,…,r)的综合语言分布评估值ms i进行集成,v=(v1,v2,…vs)(i=1,2,…,r)为消费者权重向量,得到
(四)进行二级模糊综合评价,得到考察的化妆品在总体微信购物中的语言分布评估综合评价值
设由三(二)得到的二级因素Cj(j=1,2,3,4)的权重向量为,利用语言分布评估加权算子得,
(五)计算各方案xi的综合语言分布评估值的,用xi的综合语言分布评估值的期望对方案进行排序,并选择最理想方案。综合评价值高的,就是理想方案。
四、结论
综上所述,本文对模糊综合评判法进行了改进,并将层次分析方法与改进的模糊综合评判法相融合,创造性地用于微信化妆品购物的评价中,构建了微信化妆品购物评判模型。为实际中消费者购物及微商推广产品提供了理论依据。

