悬挂式山药收获机设计与试验研究
赵国栋,李维华,2,杨发展*,杨云鹏,卞东超,郑凯瑞
(1.青岛理工大学机械与汽车工程学院,山东 青岛266520;2.山东省农业机械科学研究院,济南250100)
山药在我国栽培历史悠久,种植范围广、面积大。山药作为一种药食兼用性植物,不仅可入药,还可作为日常菜肴,药用和营养价值均较高,是目前具有良好市场前景和产业开发潜力的“药食同源”作物[1-2]。但在我国主要种植区,山药收获以人工挖掘或挖掘机侧边开沟辅助人工收获的方式为主,两种收获方式存在劳动强度大、效率低、成本高且收获完好率低等问题,大幅降低种植山药经济效益,严重影响农户种植积极性,制约山药产业发展[3-4]。山药收获机可完成开沟破土、振动碎土,将地下山药裸露,人工拔取即可完成山药收获,省力高效。因山药扎根较深和茎脆性较大的特点[5-6],山药收获机作业时仍存在易破损、菜土分离不完全等问题,此为我国山药机械化生产亟待解决的问题。
目前,我国科研机构针对山药收获技术开展系列理论和试验研究。日本对根茎类收获机械研究较早,已实现山药机械化联合作业(主要针对火山灰散碎土质)[3]。潍坊森海与山东农业大学联合研制佐佐木牌4USY—1山药收获机[7],适合我国多种种植模式且田间试验效果良好,但该机具对土壤要求较高,对土质适应能力较差,未能大面积推广使用。于万胜设计振动链输送带式山药收获机虽未进行田间试验,但为研究收获机开沟装置等关键结构提供理论基础[8]。宋帅帅等设计自走式麻山药收获机集开沟收获、土壤回填、平整土地等功能于一体,双行收获,并保证收获完好率,但此机具采用履带自走式底盘结构及双排麻山药收获,收获机体型较大、造价成本较高且仅专机专用,无法大规模推广和应用[9]。杨发展设计悬挂式山药收获机一代通过对振动碎土装置优化设计,碎土效果良好,田间试验收获完好率达89.2%,降低整机成本,但整机布局不够合理,开沟装置与振动碎土装置位于一侧,整机不平衡,且关于参数优化对收获质量影响研究不足[10]。
本文以自行研制悬挂式山药收获机为基础,对其关键部件作强度校核,针对山药收获完好率和收获效率低等问题,结合山药收获农艺特点和土壤失效破坏准则,通过振动碎土装置进行运动分析确定试验参数,开展山药收获质量试验研究,为明晰关键部件工作机理、优化其结构及试验参数、提高综合质量提供理论基础和数据支撑。
1 总体结构设计与工作分析
悬挂式山药收获机主要参数如表1所示,整机结构如图1所示,主要由悬挂装置、开沟破土装置、排土回填装置、振动碎土装置等组成,可同时实现对山药收获过程中破土开沟、提升排土、土壤回填及山药块茎与土壤分离等功能。

图1 悬挂式山药收获机整机结构简图Fig.1 The whole structure of the hanging yam harvester

表1 总体结构参数和关键部件工作参数Table 1 Overall structural parameters and working parameters of key components
收获机以三点悬挂方式安装在拖拉机后悬挂机构上,由拖拉机后输出轴提供动力输入。工作前,在山药垄头处挖一深坑便于振动碎土装置下摆入土,收获机通过拖拉机调整位置,保证两开沟链分别位于山药两侧并与作业路线平行。收获机工作时,两开沟链在拖拉机后输出轴带动下运转工作,开出两条具有一定宽度沟槽,由开沟链挖切提升带出的土壤通过横向排土螺旋排出并回填至上一行程产生的沟槽中,山药根茎则处于两沟槽间的土坯中,整机在拖拉机带动下前进,振动铲将土坯切断,通过振动将山药和土壤分离并部分裸露于土层表面,最后由工作人员捡拾山药完成收获。
2 传动系统原理分析
悬挂式山药收获机作业环境恶劣,其传动系统的设计应满足动力分配合理、整机结构紧凑、动力传递稳定的要求。收获机作业过程中动力主要用于整机升降、开沟破土、排土回填、碎土装置摆动以及振动碎土五个部分,因收获机体积较大、传动线路复杂,布局受限,仅通过传统机械传动无法全部实现五个部分的动力传递。因此,设计中综合利用液压传动的调节便捷和布局灵活等优点,通过多组液压缸和液压马达直接将动力传递到工作部件,增强传递系统柔性[11-12]。深度结合机械传动和液压传动的优势,有效提高收获机稳定性,简化机具结构,便于参数调节。
该收获机机械传动系统由拖拉机通过万向节传动将动力传递给动力输入轴,再通过齿轮传动和链传动将动力分别传递给螺旋排土器轴和开沟链轴,实现开沟破土和排土回填功能,机械传动系统具体配置如图2所示。液压传动系统分为两部分,一部分由拖拉机自带液压泵提供动力,通过两组液压缸实现整机升降和振动碎土装置摆动;另一部分以传送链与动力输入轴连接的液压泵提供动力,通过两个液压马达实现振动碎土功能,液压传动系统原理如图3所示。
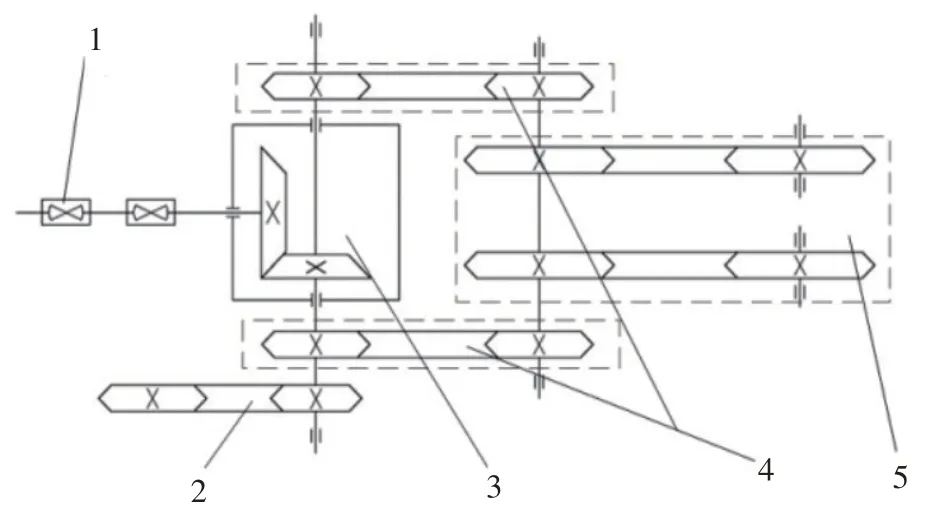
图2 机械传动系统Fig.2 Mechanical transmission system

图3 液压传动系统原理Fig.3 Schematic diagram of hydraulic transmission system
3 主要工作部件设计
3.1 开沟破土装置
山药收获时可根据山药生物学、力学特性和山药收获农艺特点获得最佳开沟深度、沟槽宽度及中间土坯宽度等作业参数,以保证山药块茎完整性并提高后续振动碎土、菜土分离质量,因此开沟破土是山药收获过程中重要一环。开沟破土装置(见图4)主要由主动链轮、从动惰轮、链条、支撑架及多种链刀等组成。其中链刀作为开沟破土装置中关键部分,可通过对链刀进行组合设计以提高开沟质量。采用三种形式链刀,分别是竖直链刀、带有一定角度链刀和圆弧杯形链刀,以两个竖直链刀,两个向内倾斜的链刀,两个向外倾斜的链刀,两个圆弧杯形链刀共4对链刀为一组,每隔一个链节安装一个链刀,交错分布,固定安装于外链板上。链刀切土分布如图4所示,a、b、c、d分别表示向内倾斜链刀对、竖直链刀对、向外倾斜链刀对以及圆弧杯形链刀对的切土范围,确保在开沟时链刀不漏切,能够将土壤完整带到排土装置中。

图4 开沟破土装置及链刀切土分布Fig.4 Ditching and soil breaking device and chain cutter cutting soil distribution
开沟破土作业中链刀会受到土壤阻力及冲击,极易遭受损坏,为保证开沟破土装置能够长时间高质量作业,对多种链刀作阻力计算并通过SolidWorks 2018作三维建模及结构静力学分析,校核链刀强度。
3.1.1 链刀切削阻力计算
链刀切削土壤阻力Ft的计算公式[13]为:
式中,Cs为土壤坚实度计的冲击次数,一般取Cs=15;δ为切削厚度,切削厚度与链刀的节距以及开沟破土装置与地面间夹角大小相关,取δ=8 mm;δc为刀片宽度,其中带角度的刀片取28 mm,竖直刀片取6 mm,圆弧杯形刀片取40 mm;φ为刀片切削角,圆弧杯形刀片的切削角与其后角相等,取12°,其余两种刀片取5°;eH为刀片尖角计算系数,取eH=0.81。经计算,竖直刀片的切削阻力Ft1=49.29 N,带有一定角度刀片切削阻力Ft2=59.52 N,圆弧杯形刀片的切削阻力Ft3=69.89 N。
3.1.2 链刀结构静力学分析
利用软件Solidworks对三种不同形式链刀进行三维建模,对链刀受力处进行分割线划分,通过Solidworks Simulation插件对三种链刀分别创建静力学分析计算,定义链刀材料属性为65 Mn[14],密度ρ=7 870 kg·m-3,泊松比μ=0.3,杨氏弹性模量E=200 GPa,屈服强度[δs]=430 MPa,其许用应力[δ]=215 MPa。对链刀两孔位置施加固定约束,将链刀受到的刀体两侧摩擦力及装填土壤重力通过切削阻力作等效处理,对链刀受到的合力施加动载系数(k=1.5)[15],按最危险情况将力均加载到链刀载荷加载面上,施加重力,采用默认方法对三种链刀作网格划分,三种链刀有限元预处理模型如图5所示。
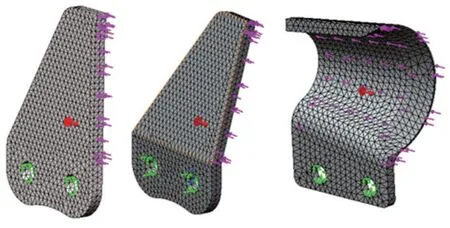
图5 链刀有限元预处理模型Fig.5 Chain knife finite element preprocessing model
由图6链刀应力云图可知,竖直刀片和倾斜刀片应力集中部位位于两孔位置处,且最大应力值为4.862和8.11 MPa,而杯形圆弧刀片的应力集中部位在刀片外侧小弧口与直板折弯处,最大应力为15.56 MPa,远小于65 Mn许用应力;由图7链刀变形云图可知,竖直刀片和倾斜刀片的最大变形位于前刀尖处,分别为0.002207和0.00312 mm,圆弧杯形刀片最大变形处位于后刀尖位置,为0.02313 mm。综上所述,三种链刀强度和刚度均满足设计要求。
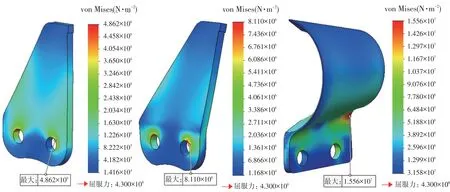
图6 链刀应力云图Fig.6 Stress cloud diagram of chain cutter
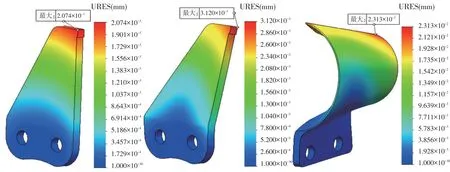
图7 链刀变形云图Fig.7 Deformation cloud map of chain knife
3.2 排土回填装置
由链式开沟装置开沟破土带至地表的土壤必须及时清除,因土壤落入沟槽造成堵塞,阻碍机具行走。目前,螺旋输送机构被认为是输送效率较高且操作简便的装置。因此,设计横向螺旋排土装置并将其安装在由链刀带出的土壤下方,使土壤能落在螺旋输送槽内,将土壤运离沟槽附近。横向螺旋排土装置结构如图8所示,规格型号选用200系列,其螺旋直径R为200 mm、螺距Pd为200 mm。设计时,横向螺旋排土装置向右侧伸出,将土壤向一侧输送至上一行程产生的沟槽中,实现土壤回填。

图8 横向排土螺旋装置结构简图Fig.8 Schematic diagram of the structure of the horizontal discharge screw device
为保证开沟装置挖掘土壤及时运走,对排土机构排土能力作校核:
开沟装置理论土壤掘出率为:

式中,H为开沟深度,取最大值H=1.3 m;lAB为开沟宽度,lAB=0.13 m;vc为机具行进速度,取作业速度最大值vc=180 m·h-1。
在实际中,开沟得到的土壤呈松散状,因此开沟装置实际土壤掘出率为:
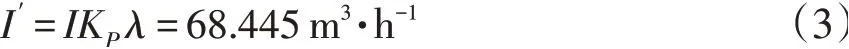
式中,KP为土壤散开系数[16],取KP=1.5;λ为与链条运动速度有关的散开系数,鉴于排土螺旋外缘速度在1.5~2 m·s-1之间,取λ=0.75。
左右螺旋输送机构的土壤输送率为:

式中,R为螺旋叶片外径,R=200 mm;r为螺旋叶片内径,r=80 mm;Pd为螺距,Pd=200 mm;n为排土机构转速,n=180 r·min-1。
可看出,开沟装置土壤掘出率小于排土机构土壤输送率,排土机构及时运走开沟装置挖掘的土壤,满足排土要求。
3.3 振动碎土装置
在山药收获机作业过程中,振动碎土装置将包含有山药块茎的土坯振动破碎,使山药与土壤分离并裸露。因此,装置设计的合理性直接影响后续挖掘收获效率、动力消耗和收获质量等,所以要对该部件进行功能和结构的精准设计[10]。振动碎土装置(见图1)主要结构包括机架、液压马达a、液压马达b、曲柄轴、格栅式振动铲、支撑梁、偏心轮、拨土连杆、拨土格栅和振动连杆等。
振动碎土装置以两套曲柄摇杆机构为基础完成设计,其中一套是由液压马达b带动的曲柄轴为主动构件,通过曲柄轴旋转带动振动连杆运动,带动作为摇杆的格栅式振动铲上下摆动,实现对中间土坯的切断和振动碎土功能。一套由液压马达a带动偏心轮转动,以偏心轮为主动构件带动拨土连杆运动,带动作为摇杆的拨土格栅左右摆动,能够去除表层土壤,实现山药块茎与土壤分离。其中,可通过调节振动连杆长度改变格栅式振动铲与水平地面间夹角,改变振动铲倾角;调节液压马达转速可改变格栅式振动铲频率和拨土格栅摆动频率,为后续性能试验提供条件。
根据常被用来计算土壤破坏的莫尔-库伦强度理论可知[17],土壤中某一处的应力状态达到极限平衡条件时会进入屈服状态濒于破坏。因此,振动碎土装置振动包含山药块茎的中间土坯,中间土坯受到振动及自身重力带来的冲击载荷,引起形变,发生相对移动使土壤间产生剪切力,当剪切力达到土壤失效力时,土壤破碎,山药块茎与土壤分离。
振动碎土装置工作时,格栅式振动铲产生的速度和加速度不断变化,中间土坯受力也不断变化,因中间土坯破碎位置不确定性,导致其运动轨迹不规则,加重土壤破碎程度。因此,可通过格栅式振动铲的运动分析,确定影响土壤受力的工作参数,控制山药块茎和土壤分离效果。
对格栅式振动铲的运动分析可通过解析法[18-19]完成。构建机构位置方程,对时间求导,即可求得机构速度和加速度方程。为便于表示格栅式振动铲位移、速度和加速度大小及方向,以曲柄轴轴心点A为原点,支撑梁轴心点D与A点连线及其垂线分别为x轴与y轴建立坐标系,如图9所示。控制格栅式振动铲振动的机构本质是简单的四杆机构,已知各杆件长度和曲柄轴角速度(ω1),将构件用矢量表示,在坐标系中作出机构的封闭矢量多边形ABCDA和机构在拖拉机带动下的行进速度(v)方向,其中E表示格栅式振动铲的铲尖。机构各矢量和为零,即机构的封闭矢量方程为:


图9 封闭矢量多边形Fig.9 Closed vector polygon
将机构的封闭矢量方程(5)改写为复数矢量形式,为:
利用欧拉公式将矢量方程的实部和虚部分离再联立求解,可以求得:
式 中,A=2l1l3sinθ1;B=2l3(l1cosθ1-l4);C=l22-l12-l32-l42+2l1l4cosθ1。
当作为原动件的曲柄轴旋转一圈,机构在拖拉机带动下行进距离S(mm)为:

式中,v为机具行进速度(m·h-1);ω1为曲柄轴转速(rad·s-1)。
则格栅式振动铲铲尖E在曲柄轴旋转一周的位移为:
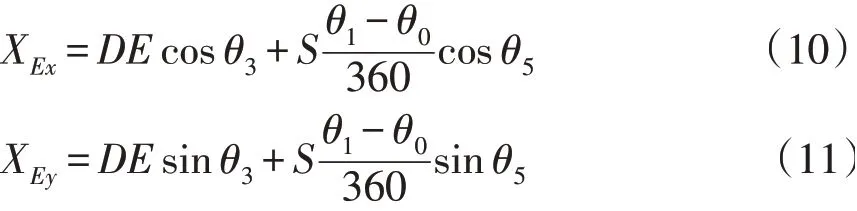
式中,DE为机构中点D、E间距离(mm);θ0为曲柄轴初始状态夹角(°)。
将封闭矢量方程的复数矢量形式(6)对时间t进行求导,可得:
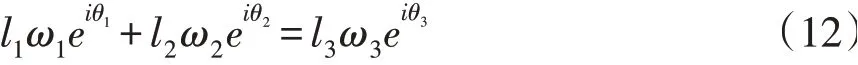
将其进行实部和虚部分离获得两分式后再联立求解,可得到构件2、3的角速度为:

格栅式振动铲绕点D摆动,则铲尖E的速度(mm·s-1)为:

因格栅式振动铲作摆动,当ω3为顺时针时,式中90°前为“+”,反之取“-”。
将式(12)对时间t进行求导,进行实部和虚部分离获得两分式后再联立求解,可得构件3的角加速度为:

则格栅式振动铲铲尖的加速度(mm·s-2)为:

其中:
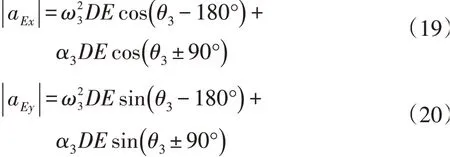
当α3为顺时针时,式中90°前为“+”,反之取“-”。
通过分析格栅式振动铲尤其是振动铲尖位移、速度和加速度,机构的四个杆件(l1、l2、l3、l4)、曲柄轴转速(ω1)及机具行进速度(v)直接影响格栅式振动铲轨迹并间接影响其速度与加速度。因此,可通过改变拖拉机行进速度改变机具行进速度v,调节振动连杆长度即格栅式振动铲倾角改变θ3,调节液压马达转速改变曲柄轴转速ω1大小,影响格栅式振动铲轨迹、速度及加速度,改变土壤受力,因此可通过试验确定最大土壤破碎效率且山药收获完好率最高的最优参数组合。
4 田间性能试验测试
4.1 试验条件与方法
试验于2020年12月2~4日在青岛平度市张舍镇潘家洼村进行。试验山药品种为白玉山药,单垄单行种植模式,垄距1 200 mm,株距250~400 mm,深为900~1 200 mm。试验地面积1 000 m2(200 m×5 m),共种植4垄山药,土壤类型为壤土。
从试验地块中随机选取30个测试区,每个测试区内有单垄山药,测试区长10 m,30次试验,收获机悬挂于拖拉机上,保持拖拉机匀速行驶,开沟深度保持恒定,实验员跟随驾驶人员在田间进行收获试验,测试仪器包括米尺、电子秤、转速传感器、位移传感器等。
4.2 性能试验
选取曲柄轴转速X1、机具行进速度X2、振动铲倾角X33项对山药收获质量影响较大的工作参数作为试验因素(见表2)。开沟深度(1 300 mm)、作业幅宽(550 mm)等其他试验参数保持不变。试验以山药收获完好率Y1、山药收获生产率Y2作为指标,进行三因素三水平响应面试验(见表3)[20-21]。

图10 田间试验现场Fig.10 Field trial site

表2 响应面试验因素水平Table 2 Response surface test factor level

表3 响应面试验设计方案与结果Table 3 Response surface test design scheme and results
4.3 回归模型建立与显著性检验
通过Design-Expert软件[22-23]对三因素三水平中数据进行多元回归拟合分析,建立Y1、Y2对X1、X2、X3的响应面回归模型:

回归方程方差分析如表4所示,完好率Y1和生产率Y2的P值分别<0.0001和0.0002,均小于0.05,且失拟项的P值为0.4919和0.3814,均大于0.05,表明这两个模型影响极显著且拟合程度较高,拟合方程决定系数R2分别为0.9835和0.9704,说明回归方程可解释97%以上的评价指标。因此,可通过这两个回归方程优化收获机工作参数。

表4 回归方程方差分析Table 4 Analysis of variance of regression equation
4.4 交互因素对性能影响规律分析
探究曲柄轴转速、机具行进速度及振动铲倾角交互作用对山药收获完好率及生产率的影响,利用Design-Expert软件绘制响应面。交互因素对山药收获完好率及生产率影响响应面曲线如图11、12所示。
图11(a)表明减小机具行进速度,适当增加曲柄轴转速可提高收获完好率,而曲柄轴转速过大减小收获完好率;图11(b)表明适当减小振动铲倾角并增加曲柄轴转速有助于提高收获完好率,振动铲倾角和曲柄轴转速过小降低收获完好率;图11(c)表明减小机具行进速度,适当减小振动铲倾角有助于提高收获完好率。图12(a)表明增加机具行进速度有助于提高生产率;图12(b)表明曲柄轴转速和振动铲倾角对生产率影响不大;图12(c)表明增大机具行进速度可提高生产率。
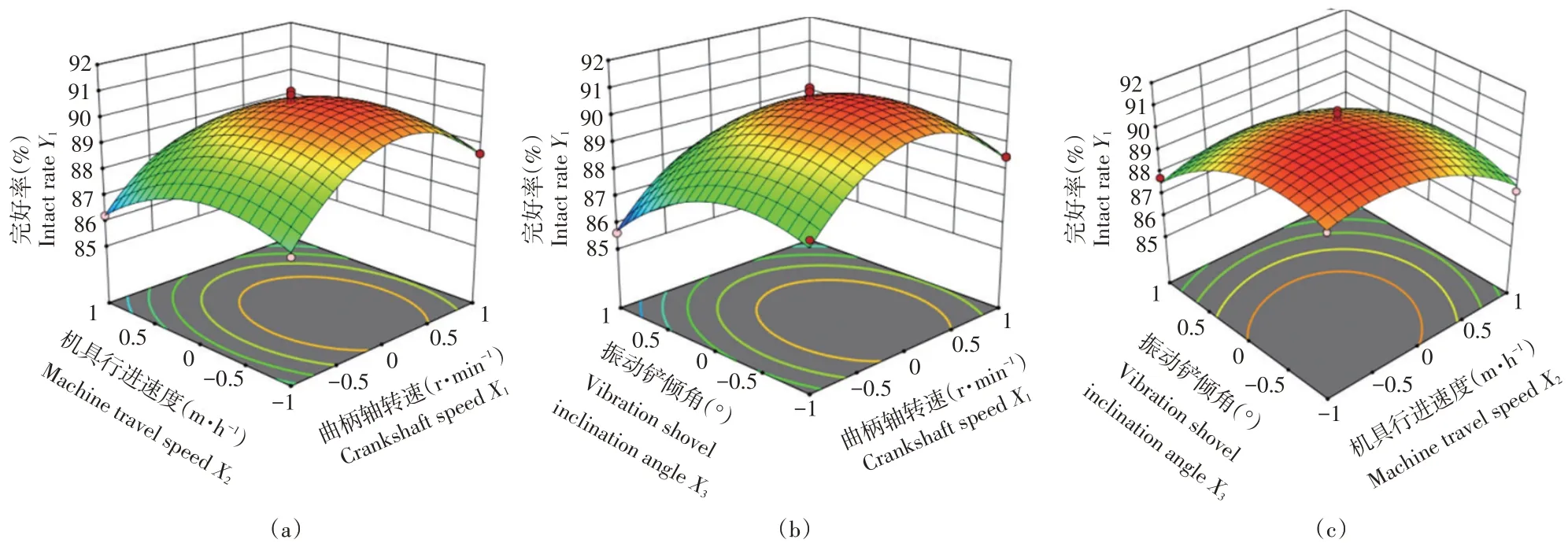
图11 交互因素对收获完好率影响的响应面图Fig.11 Response surface diagram of the influence of interaction factors on the harvest intact rate

图12 交互因素对生产率影响的响应面图Fig.12 Response surface diagram of the impact of interactive factors on productivity
4.5 试验优化与验证
山药在机械化收获过程中,其完好率是最重要指标,利用Design-Expert软件优化求解模块可以求得约束条件下最大收获完好率的最优参数组合。最优参数组合为:曲柄轴转速306.18 r·min-1、机具行进速度137.85 m·h-1及振动铲倾角-6.18°,对应收获完好率为90.984%。试验于2020年12月18日在相同地点开展验证试验,山药收获完好率为90.855%。与第一次试验收获完好率平均值对比,增加2.435%,性能明显改善。
5 结论
a.研究设计一种悬挂式山药收获机,可同时实现对山药收获过程中破土开沟、排土、土壤回填及山药与土壤分离等功能,收获完好率及生产率高,有效降低人工成本,提高经济效益。
b.在对山药收获机整机工作原理分析基础上,研究整机关键部件结构设计和参数确定。利用Solidworks软件对链刀作结构静力学分析,链刀最大应力为15.56 MPa、最大位移为0.02313 mm,满足强度及刚度要求,可确保长时间高质量开沟作业;通过土壤失效破碎理论及格栅式振动铲运动分析,确定可通过调节曲柄轴转速、机具行进速度及振动铲倾角改变土壤破碎效果,为后续提高果土分离质量试验提供理论支撑。
c.借助Design-Expert软件,选取曲柄轴转速、机具行进速度及振动铲倾角3个因素为影响因子,开展三因素三水平试验,分析各因素对收获完好率及生产率的影响并优化。结果表明,最大收获完好率最优参数组合为曲柄轴转速306.18 r·min-1、机具行进速度137.85 m·h-1和振动铲倾角-6.18°,较第一次收获完好率增加2.435%,性能改善。

