基于ARIMA 模型预测Bitcoin 价格的研究

摘要：随着数字经济的快速发展，比特币成为当代重要的金融讨论话题。比特币是一种基于区块链技术，保证整个支付体系和虚拟货币产生和使用的点对点协议，比特币具有去中心化、匿名性和内置激励性等特征，缺点是缺少信用背书、币值不稳定和发行者过多占据 “铸币税”。由于比特币主要扮演的是资产角色而非充当货币角色，其市场投机性强和币值波动性大的特点，因而和其他投资市场相比，因而比特币存在市场效率低下的现象，故研究比特币价格的预测与分析具有重要意义。本文主要选用2019年3月到2021年7月的比特币收盘价，采用了ARIMA模型，通过使用R语言对数据进行平稳化处理并进行单位根检验，对比各参数，建立合理的ARIMA模型，同时，与自动生成的ARIMA模型进行比较，选择较为优良的模型进行比特币价格的短期预测。

关键词：比特币;ARIMA模型;时间序列

引言

2008年10月，一位名为中本聪密码学者发布了《比特币： 一种点对点的电子现金系统》的文章，文内描述了一种被他称为“比特币”的电子货币及其算法。随后，中本聪挖出第一个区块，即所谓的创世区块，由此比特币正式诞生。比特币是基于区块链技术，具有分布式账本、可追溯、不可篡改、去中心化等特点，为金融创新带来了新的可能。在比特币出现后，还有以太坊、瑞波币等基于区块链技术的数字货币大量涌现。

比特币的底层技术是区块链。区块链，顾名思义是由“区块”和 “链”组成的。区块简单而言就是一个信息块，通过加密算法记录交易信息，如果区块的交易信息被认证、接受，那就可以写入链条中，并发布给所有的节点，形成区块链。所以说，区块链可以理解为一个严格按照时间顺序排列的交易信息记录簿，而且分布在所有节点上。

2009年10月，1美元相当于1309. 03比特币;2010年11月6日，第一个比特币交易所成立，1比特币相当于0.5美元;此后，比特币的价格出现飞跃式上涨，在2013年11月涨至超过1000美元的历史高点;2014年2月，当时世界最大的比特币交易所 Mt. Gox 被盗，引发虚拟货币历史上的第二次大熊市;到2020年，比特币的价格暴涨，又回到超过 1 万美元的高位。可见比特币的价格是极度波动的，而随机的、大幅的波动性，使得以比特币为载体的商业交易面临着极大的不确定性，同时比特币主要用于资产而非货币，在金融市场和投资组合管理中发挥重要作用，因此，对比特币波动性的研究具有重要的现实意义。

1.时间序列模型——ARIMA模型

假设时间序列{X_t}具有如下形式：

X_t=φ_0+φ_1 X_（t-1）+φ_2 X_（t-2）+...+φ_p X_（t-p）+ε_t-θ_1 ε_（t-1）-θ_2 ε_（t-2）-...-θ_q ε_（t-q）  （1）则称式（1）为自回归移动平均模型，记为 ARMA（ p，q） 模型，称{X_t}为ARMA（ p，q）过程，其中，E（ε_t）=0，var（ε_t）=σ_ε^2，cov（ε_t，ε_t）=0（s≠t），cov（x_s，ε_t）=0（∀s<t）

如果一个时间序列{X_t}的d次差分Wt = ∇^d X_t时ARMA（p，q）过程，

即 W_t=φ_1 W_（t-1）+φ_2 W_（t-2）+...+φ_p W_（t-p）+ε_t-θ_1 ε_（t-1）-θ_2 ε_（t-2）-...θ_q ε_（t-1）   （2）

则称上式（2）为自回归滑动平均求和模型，记为ARIMA（p，d，q）模型，称{X_t}为ARIMA（p，d，q）过程。当 d = 0，ARIMA（p，0，q） 模型实际上就是 ARMA（p，q）;当 p = 0，ARMA（0，d，q） 模型可以简记为IMA（d，q） 模型;当 q = 0 时，ARMA（p，d，0）模型可以简记为ARI（p，d）模型。

ARIMA模型是差分整合移动平均自回归模型，又称整合移动平均自回归模型，是时间序列预测分析方法之一。通常对线性趋势可以用一阶差分可以使之平稳化，对二阶曲线使用二阶差分。在实际应用过程中，可能由于过差分使数据失真，因此产生了分数阶差分来进行优化，本文使用一阶差分，因此对分数阶差分不再赘述。

2.实证分析

2.1建立时间序列

本文所使用的数据主要是2019年10月至2021年1月比特币交易平台指数的每日收盘价原始数据。这些数据在http：//www.coindesk上公开，选取数据包中的收盘价作时间序列。

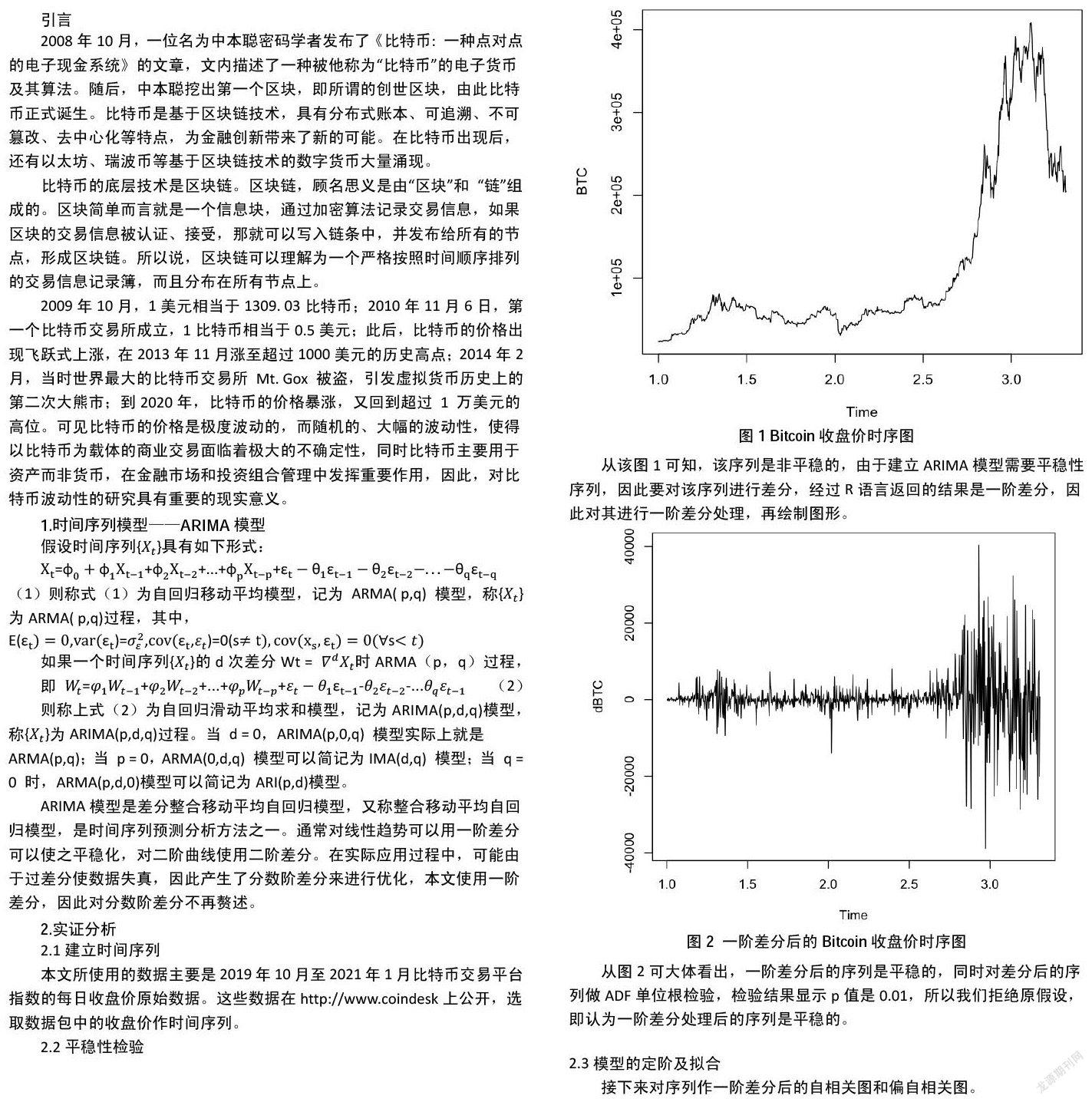
2.2平稳性检验

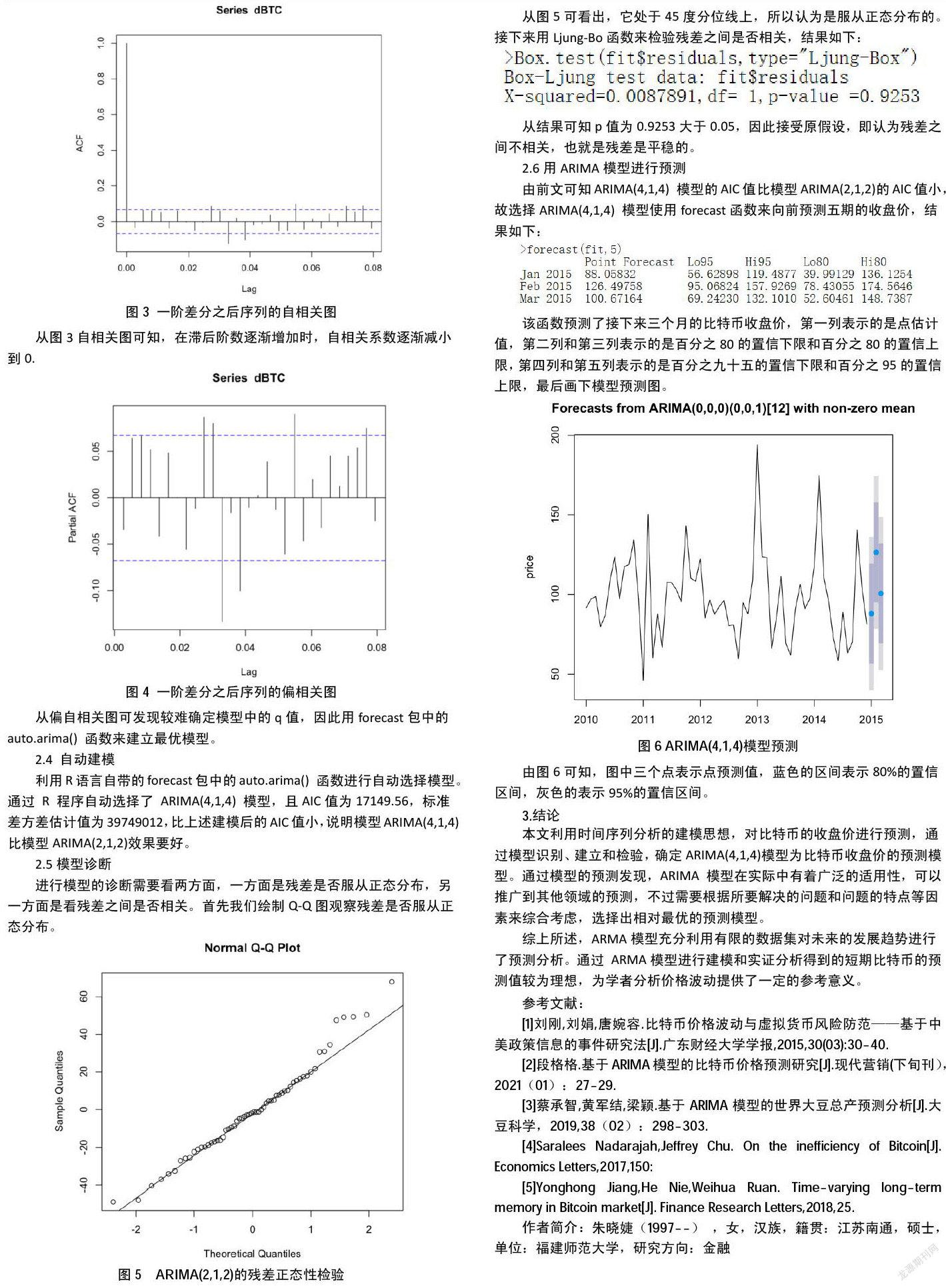
从该图1可知，该序列是非平稳的，由于建立ARIMA模型需要平稳性序列，因此要对该序列进行差分，经过R语言返回的结果是一阶差分，因此对其进行一阶差分处理，再绘制图形。

从图2可大体看出，一阶差分后的序列是平稳的，同时对差分后的序列做ADF单位根检验，检验结果显示p值是0.01，所以我们拒绝原假设，即认为一阶差分处理后的序列是平稳的。

2.3模型的定阶及拟合

接下来对序列作一阶差分后的自相关图和偏自相关图。

从图3自相关图可知，在滞后阶数逐渐增加时，自相关系数逐渐减小到0.

从偏自相关图可发现较难确定模型中的q值，因此用forecast包中的auto.arima（） 函数来建立最优模型。

2.4 自动建模

利用R语言自带的forecast包中的auto.arima（） 函数進行自动选择模型。通过 R 程序自动选择了 ARIMA（4，1，4） 模型，且AIC值为17149.56，标准差方差估计值为39749012，比上述建模后的AIC值小，说明模型ARIMA（4，1，4）比模型ARIMA（2，1，2）效果要好。

2.5模型诊断

进行模型的诊断需要看两方面，一方面是残差是否服从正态分布，另一方面是看残差之间是否相关。首先我们绘制Q-Q图观察残差是否服从正态分布。

从图5可看出，它处于45度分位线上，所以认为是服从正态分布的。接下来用Ljung-Bo函数来检验残差之间是否相关，結果如下：

从结果可知p值为0.9253大于0.05，因此接受原假设，即认为残差之间不相关，也就是残差是平稳的。

2.6用ARIMA模型进行预测

由前文可知ARIMA（4，1，4） 模型的AIC值比模型ARIMA（2，1，2）的AIC值小，故选择ARIMA（4，1，4） 模型使用forecast函数来向前预测五期的收盘价，结果如下：

该函数预测了接下来三个月的比特币收盘价，第一列表示的是点估计值，第二列和第三列表示的是百分之80的置信下限和百分之80的置信上限，第四列和第五列表示的是百分之九十五的置信下限和百分之95的置信上限，最后画下模型预测图。

由图6可知，图中三个点表示点预测值，蓝色的区间表示80%的置信区间，灰色的表示95%的置信区间。

3.结论

本文利用时间序列分析的建模思想，对比特币的收盘价进行预测，通过模型识别、建立和检验，确定ARIMA（4，1，4）模型为比特币收盘价的预测模型。通过模型的预测发现，ARIMA 模型在实际中有着广泛的适用性，可以推广到其他领域的预测，不过需要根据所要解决的问题和问题的特点等因素来综合考虑，选择出相对最优的预测模型。

综上所述，ARMA模型充分利用有限的数据集对未来的发展趋势进行了预测分析。通过 ARMA模型进行建模和实证分析得到的短期比特币的预测值较为理想，为学者分析价格波动提供了一定的参考意义。

参考文献：

[1]刘刚，刘娟，唐婉容.比特币价格波动与虚拟货币风险防范——基于中美政策信息的事件研究法[J].广东财经大学学报，2015，30（03）：30-40.

[2]段格格.基于ARIMA模型的比特币价格预测研究[J].现代营销（下旬刊），2021（01）：27-29.

[3]蔡承智，黄军结，梁颖.基于ARIMA模型的世界大豆总产预测分析[J].大豆科学，2019，38（02）：298-303.

[4]Saralees Nadarajah，Jeffrey Chu. On the inefficiency of Bitcoin[J]. Economics Letters，2017，150：

[5]Yonghong Jiang，He Nie，Weihua Ruan. Time-varying long-term memory in Bitcoin market[J]. Finance Research Letters，2018，25.

作者简介：朱晓婕（1997--） ，女，汉族，籍贯：江苏南通，硕士，单位：福建师范大学，研究方向：金融