梯形明渠流速分布及水位流速法流量测量分析
王晓风
(甘肃省武威水文水资源勘测局,甘肃 武威 733000)
水利明渠设计、建造和运行管理中,流速分布和流量测量是必不可少的水工技术指标。现有明渠流量测量方法有:(1)流速面积法,需要人工操作,虽然检测精确度很高,但是不能达到自动化需求;(2)堰槽法,可以自动化检测,操作较容易测量结果亦准确,但需部分改建明渠结构,投资较大,且明渠中的淤泥变动会影响此方法的测量精确度;(3)仪器测量法,诸如电磁流量计,多普勒法流量计等,也操作简洁,测量准确,但存在仪器价格昂贵,维护费用高,仍不能轻易满足面广量多的流量自动检测要求。(4)流量水位关系法,胜任自动检测,但测量精确度相对低,结果仍不够准确;(5)漂浮物法、稀释法、动船法、面积比降法等,操作不够简洁,测量比较粗略,更多适用于非自动小型明渠的检测。本研究针对现有明渠截面流量检测方法的短板,尝试探究一种规则截面流量自动检测的方法“水位流速法”,并通过案例干渠截面流量检测与“面积流速法”实地测量结果对比,验证“水位流速法”的检测准确性及适用性。
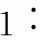
1 明渠截面垂线流速分布及验证
1.1 垂线流速分布规律
对于梯型截面垂线流速分布说来,宽深比、糙率、垂线部位是关键功效影响要素;在底部内区水深y/H与无量纲标准化流速u/V(v是垂线均流速,U是点流速)二者关系呈对数分布态,但于底部外区(水深y/H>0.6范围),会逐渐呈乘幂函数分布态势。所以用对数计算公式u/V=a+bln(y/H)和乘幂计算公式(u-us)/V=a(1-y/H)b(公式中us系表面流速,通常取us=1.05V),来分别解析梯型截面明渠底部内区、外区垂线流速分布。这比以往整个区域都用对数分布规律相对更为合理。拟合功效见图1及图2所示具体所示。

图1 底部内区流速基于对数公式的拟合图

图2 外区和表面区基于幂函数的流速拟合图
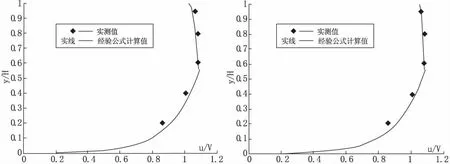
本研究在底部内区以u/V=a+bln(y/H)表达垂线流速分布,表面区及外区以(u-us)/V=a(1-y/H)b表达垂线流速分布。幂函数和对数公式当中,常数受糙率和测线距边坡的平向部距离影响较大,因明渠实际糙率通常为n=0.014和n=0.03,为简化问题,特把梯型渠的流速分布以n=0.014和n=0.03获得经验计算公式。故在糙率既定状态下,此时影响待定常数的重点要素只有B/H及Z/H。底部内区流速基于对数公式u/V=a+bln(y/H)的拟合结果见表1,底部外区流速拟合结果见表2。

表1 底部内区流速基于u/V=a+bln(y/H)的拟合结果
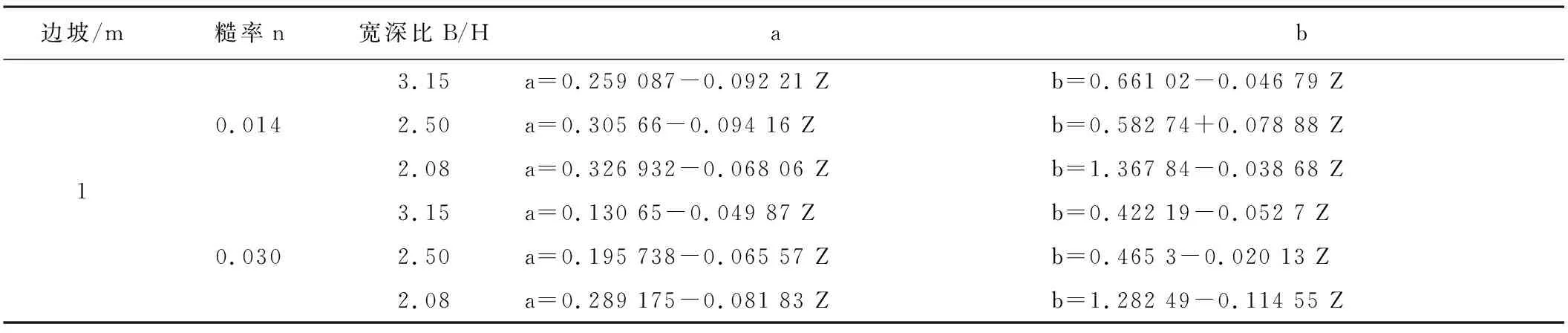
表2 底部外区流速基于(u-us)/V=a(1-y/H)b的拟合结果
1.2 垂线流速分布规律的验证
把按上述经验公式计算所得流速值跟案例外黄支(糙率系,水深系,纵坡系,边坡系)的流速实地测量值开展对比,结果如图3和表3具体所示。
Z=1.14 Z=1.93

表3 案例外黄支截面实测值与流速经验公式的模拟计算值比对
由图表发现,在用对数计算公式拟合该区流速时,流速经验公式所得值与实测值亦很接近,达到7%之内误差。当水深相对是0.4~0.6时,其计算值与实测值更接近。用式(u-us)/V=a(1-y/H)b拟合表面区和外区流速时,相对误差5%内,二者同样更接近。显示流速模拟计算经验公式可以很准确的来说明梯型明渠中实际流速分布情况。
2 垂线均流速的平向分布及验证
2.1 垂线均流速的平向分布规律
窄深梯型明渠的垂线均流速沿平向分布趋势为靠近边壁快速加增,远离则保持基本不变,故选择Vi/Vmax=p(xq/(kq+xq))计算明渠垂线均流速沿平向分布,其拟合计算结果具体见表4所示。
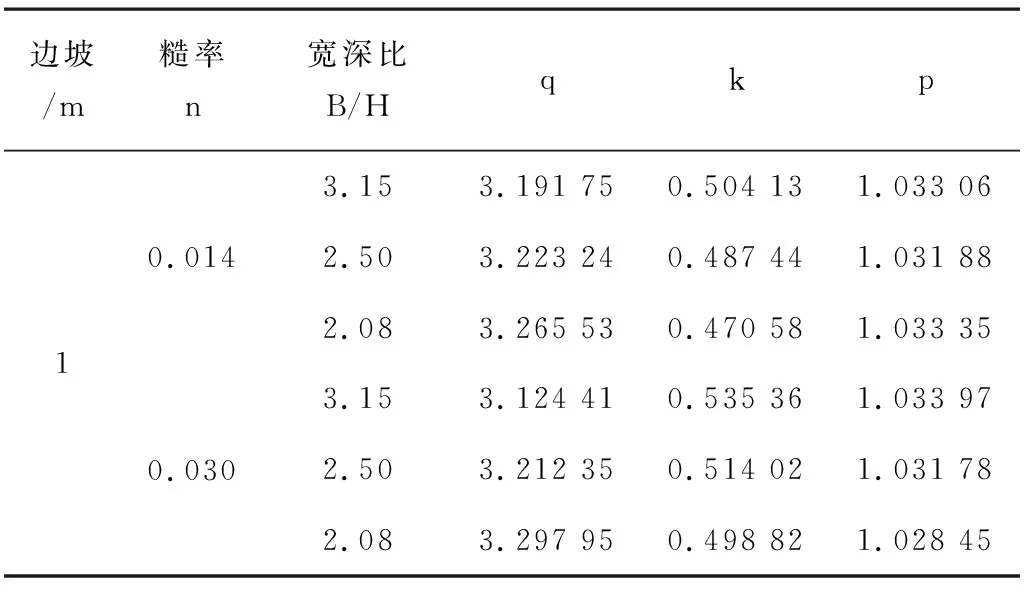
表4 垂线均流速平向分布基于Vi/Vmax=p(xq/(kq+xq))的拟合计算结果
2.2 垂线均流速的平向分布规律验证
为验证垂线均流速沿平向的分布计算公式,本研究把据经验计算公式得到的垂线均流速分布结果与案例外黄支(水深是0.8 m,纵坡是1/7 000)截面实地测量垂线均流速值开展对比,这里给出两者对比的左侧对比图具体见图4所示。

图4 经验公式计算值与现场值的比较
图4对比曲线揭示,实地测量与垂线均流速沿平向分布计算公式所得到的计算结果十分吻合,显示本研究所提出的垂线均流速平向分布规律是可靠合理的。
3 明渠截面流量的水位流速法检测
3.1 检测原理
“水位流速法”是根据明渠截面流速分布经验计算公式,测出截面某点流速、渠底泥位以及截面水位后,经过计算得到截面流量。该方法基本原理为:把截面分成数个分区(见图5具体所示),测出截面某一点(配置流速仪,此点绝对位置即被固定)的流速、渠底泥位以及截面水位后,依据截面垂线流速分布规律、水深值、测点流速以及测点部位,获得测点的垂线均流速。依据垂线均流速平向分布规律获得各分区的中垂线均流速,该中垂线均流速替代各分区均流速,求得各分区流量后再汇总获得截面总流量。

图5 水位流速测量法明渠截面流量示意
运用“水位流速法”检测明渠截面流量时,按前述基本原理,先把明渠截面均分为个分区,再计算各分区流量并汇总,获得明渠截面总流量。计算公式:
(1)
式中:Hm系截面中垂线处水深;B系水面宽度;ΔSi系第i个分区面积;vi系该区中垂线等效均流速(分区中垂线均流速是矩型截面明渠的值;梯型截面明渠,值是分区中垂线均流速Hi/Hm倍,Hi是中垂线处水深),梯型及矩型截面明渠,vi按式(5)、(2)计算。梯形截面明渠等效垂线均流速和矩形截面明渠垂线均流速平向分布规律:
V1/Vmax=p(2Zi/B)q/[kq+(2Zi/B)q]
(2)
式中:Zi系第i个分区的中垂线到左侧边壁的距离;Vmax系截面中垂线均流速;q,p,k均为常数。矩形和梯形截面明渠底部内区垂线流速分布规律为:
(3)
矩形截面明渠外区和表面区垂线流速分布规律为:
(4)
梯形截面明渠外区和表面区垂线流速分布规律为:
(5)
前述三公式中,H系水深;y系测点到渠底的高;V系垂线均流速;u系测点流速;us系表面流速,通常取us=1.05v;c、b、a均为常数。
3.2 检测过程
(1)按图5配置泥位仪、水位仪及在线流速仪,自动检测渠底泥、水位及点流速位。
(2)把所测截面分成2个相等分区,依据测出的泥位、水位及点流速,计算截面分区中垂线均流速和水深。
(3)取第i个分区为例,中垂线均流速vi计算过程如下:一是依据截面水深H和测点部位y得知测点水深, 继而确定测点系属外区或者内区;二是依据上步结果和水面宽B、糙率n及明渠边坡常数m等,借助式(3)、式(4)或者式(5)计算Vmax;三是根据Vmax及式(2)计算Vi。前述Vi计算中,隐含测点配置于截面中垂线上,且实际测量中亦通常配置于截面的中垂线上。如果测点不在截面中垂线,第2)步则应先依据式(5)、式(4)或者式(3)算出测点处的垂线均流速;再依据式(2)计算出截面中垂线均流速Vmax;依据式(2)和所得Vmax,最后求得vi。
(4)用分区中垂线均流速替代各分区均流速,依据式(1)计算出各分区流量,求其和即截面总流量。
3.3 对比验证
检验“水位流速法”检测明渠截面流量的适用性及准确性,选取案例某外黄支和西干渠首截面,依据截面检测水深、固定测点流速和流速分布经验计算公式,应用“水位流速法”,得出2截面在特定时段(检测截面流量时长)的时均流量值;再应用“面积流速法”,检测出同时段案例截面的实测流量;两者比对结果具体见表5所示。

表5 计算流量与实测流量的比较
实测流量选用“面积流速法”获得。即在测流截面上配置n+1条垂线测速,配置六个测点在各条测速垂线上,分区以测速垂线为边界,把明渠截面划分为n个分区,依据水深和实测流速,计算各分区流量,最后把各分区流量开展求和获得截面流量。
由表5数据揭示,西干渠首截面,用“水位流速法”与实测所得流量之间误差仅4.5%,外黄支截面用“水位流速法”与实测所得流量之间误差仅2.2%,显示“水位流速法”检测明渠流量是可靠准确的。
4 结语
本研究对梯形截面明渠垂线流速分布规律以及垂线均流速的平向分布规律进行了阐述验证,并在介绍流速分布经验公式基础上提出了明渠截面流量的水位流速测量方法。文中概要梳理介绍了测量原理到测量过程,并基于案例渠道截面流量测量,对“水位流速法”和“面积流速法”实测结果进行了对比,结果显示“水位流速法”计算流量与“面积流速法”实测流量相对误差低于4.5%,最小误差仅2.2%,表明“水位流速法”检测明渠截面流量是准确可行的。另因为渠底泥位、水位及点流速很容易完成在线检测,因此“水位流速法”也将具有良好的明渠截面流量自动测量的工程应用价值。

