基于模糊算法的AUV避障与姿态控制

刘 用， 杨晓飞， 夏金铭

(江苏科技大学 电子信息学院， 江苏 镇江 212003)

从古至今，人类对海洋的探索就从未停歇，广阔的海洋拥有丰富的可再生资源和矿产资源.随着科技的发展，人们对海洋的探索得到了进一步的发展，水下机器人(autonomous underwater vehicle，AUV)应运而生，水下机器人是用来对海洋开发、深海探测和水下作业的一种水下无人平台.然而，AUV控制器面临高维度、强耦合、非线性以及复杂的海水环境等重要因素导致的数学模型参数不稳定，会对AUV的避障与姿态控制变得困难.从国内外的发展现状来看，AUV的自主控制仍是一大难题.

路径规划问题作为水下机器人的基本环节，很多学者对其进行了研究.黄朝熙等[1]提出了一种利用单波束声纳的探测波束依次旋转的方法获取AUV附近的障碍物信息，成功实现了AUV躲避开角的障碍物.张汝波等[2]提出了一种运用蚁群间信息素调整准则的方法，成功应用到了AUV航路多重避障的模型中.庞师坤等[3]针对AUV在海底可能遇到的静动态障碍物问题，设计了基于零空间行为法的避障策略，在复杂障碍物环境中达到了预期的避障效果.姚鹏等[4]提出了一种高效的修正导航向量场的方法，成功应用在复杂海洋环境下的AUV避障任务.孙兵等[5]提出了一种基于粒子群优化的模糊路径规划算法，有效地对动静态障碍物进行了避障路径规划.张楠楠等[6]针对自主式水下机器人的三维避障最优路径问题，提出了一种适用于全局路径规划的改进蚁群算法，在大尺度海底环境下仿真验证了该算法的有效性.王超等[7]将速度合成的方法与人工势场相结合，克服了海流对AUV水下航行的影响.时常鸣等[8]研究了一种基于混合整数线性规划的AUV与水下移动平台对接的实时路径规划方法，在仿真试验下，验证了方法的有效性.徐言民等[9]针对水下复杂环境、障碍物不规则、规划困难等问题，提出了适用于三维空间路径规划的空间分层路径规划方法并验证了方法的有效性.付振秋等[10]提出一种粒子群融合算法，充分利用粒子群算法较强的全局搜索能力，通过仿真验证了该方法的有效性.朱大齐等[11]提出了一种基于改进模糊的全覆盖路径规划算法，使AUV能够自动避开各类静态和动态障碍物，自动逃离路径的死锁区.LIANG X.等[12]研究了欠驱动自主水下航行器在模型不确定性和时变干扰等复杂未知条件下的三维轨迹跟踪问题，在时变参考轨迹的基础上，进行了运动学上的俯仰角和偏航角的设计,通过仿真验证了所提方案的有效性和优越性.

为了实现对AUV的避障与姿态控制，笔者结合模糊算法的优点，分别设计AUV在水平面和竖直面的模糊控制器，实现AUV的避障与姿态控制.

1 AUV系统结构

AUV三维模型结构如图1所示，在AUV机体上，配置了5个声纳(图1中1-5)，分别用来探测AUV在水下航行时，上方、右方、前方、左方和下方的障碍物；配置在AUV机体上的推进器(图1中a-f)通过模糊算法，输出向左、向右和下潜加速度.

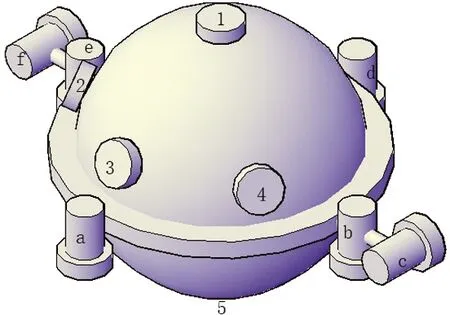
图1 AUV三维模型结构图

将AUV所在的三维平面分为水平二维平面和竖直二维平面，在水平面上，左右2个声纳与正前方的声纳的夹角均为60°，3个声纳分别用来探测AUV左、前和右方的障碍物；向左推进器和向右推进器用来控制AUV的水平方向上的前进速度和摇艏角速度；在竖直面上，上下2个声纳与正前方的声纳的夹角均为90°，3个声纳分别用来探测AUV上、前和下方的障碍物；推进器用来控制AUV的竖直方向下潜加速度.

2 基于模糊算法的三维避障决策设计

2.1 水平面避障决策的构建

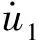
采用if-then构建的水平面模糊规则如表1所示.

表1 水平面模糊规则

使用重心法(center of gravity，COG)去模糊化，可得

(1)

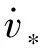
对于模糊控制器输出的AUV的左、右加速度进行积分，可得

(2)

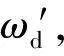
(3)

式中：L为向左和向右推进器之间的距离.

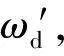
(4)

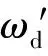
(5)

式中：kr为摇艏角速度的阻尼系数.

2.2 竖直面避障决策的构建

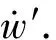
综上所述，采用if-then构建模糊规则，得到的竖直面模糊规则如表2所示.

表2 竖直面模糊规则

对于w′，系统同样不稳定，通过引入阻尼系数，可将下潜速度期望指令设计为

(6)

式中：kw为下潜速度的阻尼系数.

3 AUV姿态控制

由拉格朗日方程可得，AUV的运动数学模型为

(7)

式中：η=(x,y,z,φ,θ,ψ)T,x、y、z、φ、θ、ψ分别为惯性坐标系中的前进位移、横移位移、竖直位移、横倾角度、纵倾角度和摇艏角度；J(η)∈R6×6为转换矩阵；τ为推进器产生的力和力矩，τ∈R6；v=(u,v,w,p,q,ω)T，u、v、w、p、q、ω分别为机体坐标系中的前进速度、横移速度、下潜速度、横倾角速度、纵倾角速度和摇艏角速度；MRB为刚体惯性矩阵；MA为附加质量矩阵；CRB为科里奥利力矩阵；CA为附加科里奥利力和向心力矩阵；D(v)为阻尼矩阵；G(η)为恢复力矩阵[13].

令M=MRB+MA，C(v)=CRB+CA，可得动力学方程为

(8)

AUV在复杂海水环境中工作时遇到的干扰以及不确定性等通常体现在动力学方程不确定的参数上，因此，考虑到动力学参数的不确定性，得到新的动力学方程为

(9)

式中：ΔC和ΔD为动力学不确定参数.

将AUV的期望速度指令定义为

vd=(ud,0,wd,0,0,ωd)T.

(10)

则速度跟踪误差为

ξ=v-vd.

(11)

对速度跟踪误差求导,并结合式(9),可得含不确定参数的非线性系统为

M-l[τ-(C(v)+ΔC)v-(D(v)+ΔD)v-

(12)

令

(13)

式中： Δf(v)为未知不确定项.

由式(13)可得

(14)

式中：u=M-1τ.

选择模糊逻辑[14]逼近未知不确定项Δf(v)=(Δf1(v),Δf2(v),…,Δfk(v)).模糊推理机使用模糊if-then规则，执行从输入语言向量v到输出变量w∈R的映射.第l条模糊规则可表示为

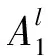
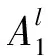
具有单变量模糊器、乘积推理机和中心平均解模糊器的模糊系统的输出可以写成：

(15)

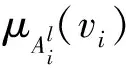
因此，Δf(v)的逼近可以表示为

(16)

通过模糊算法对不确定项进行逼近后，可据此选择合适的李雅普诺夫函数：

(17)

对式(17)求时间导数，可得

(18)

(19)

式中：k=diag(k1,k2,k3,k4,k5,k6)，k1、k2、k3、k4、k5、k6为正常数.

将式(19)代入式(18)得

(20)

因此，可以得到自适应律如下：

(21)

至此，对AUV速度的控制律和自适应律设计已完成，分别为式(19)、(21).

4 仿真与分析

设置目标在(200,200,200)m，障碍物中心分别在(0,10,110)和(140,140,190)m，半径均为25 m时，经过640 s仿真后，AUV的轨迹曲线如图2所示,AUV在遇到第1个障碍物时，从下方绕过了障碍物，之后继续向目标前进；当遇到第2个障碍物时，AUV从右方绕过障碍物，最终到达目标位置.

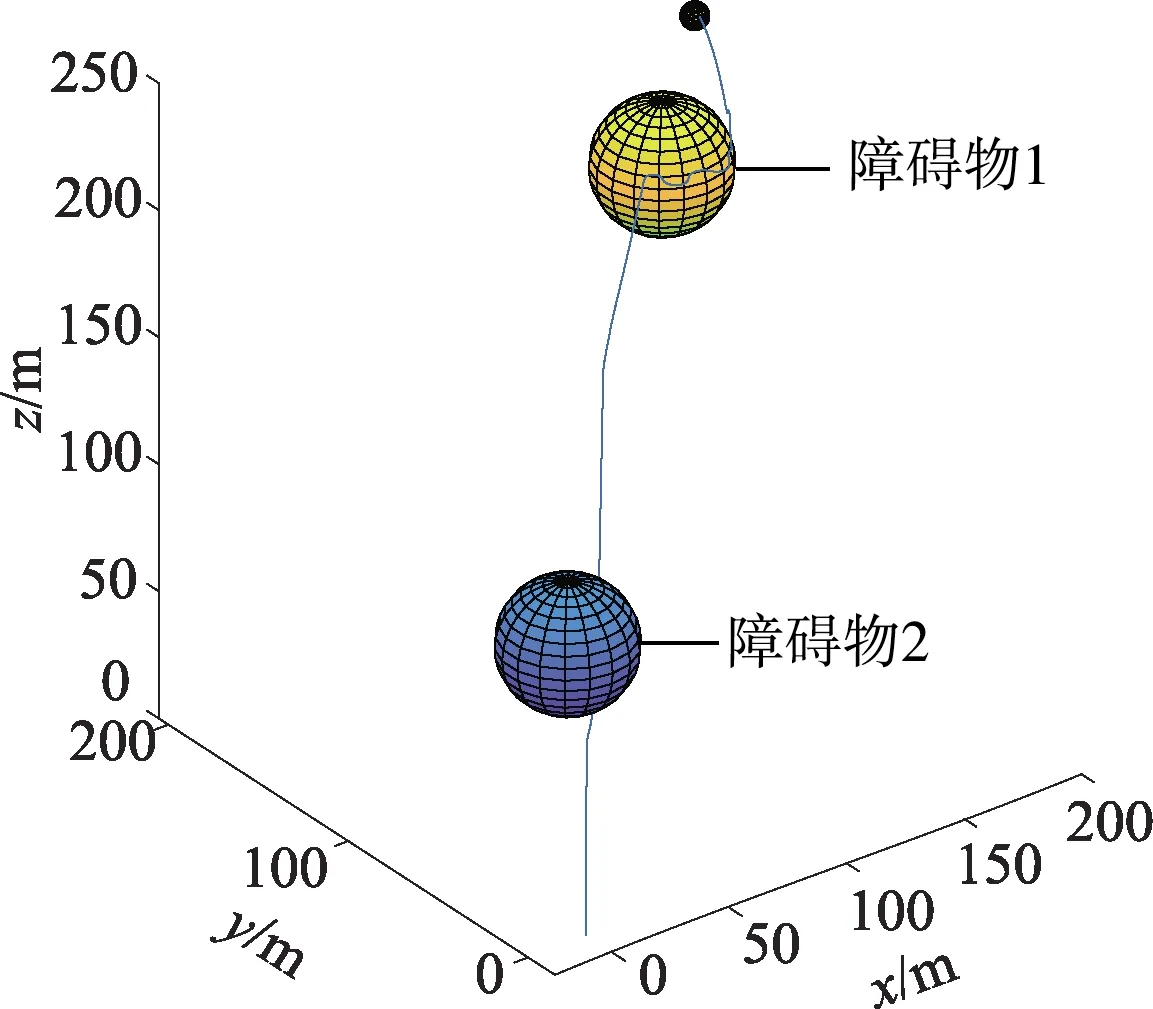
图2 AUV的轨迹曲线

AUV速度指令如图3所示.

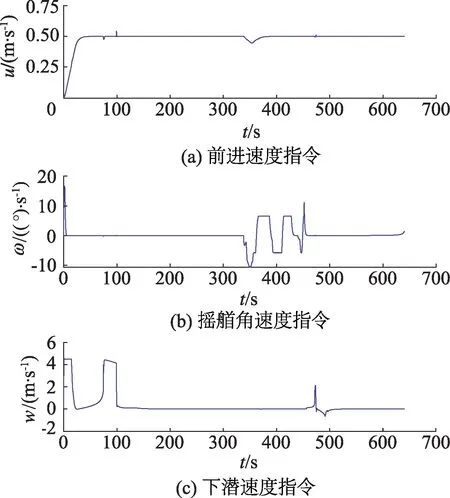
图3 AUV速度指令

从图3可以看出：AUV一直保持较稳定的前进速度；遇到第1个障碍物时，通过调整下潜速度，成功绕开了第1个障碍物，之后重新调整下潜速度；当遇到第2个障碍物时，通过调整摇艏角速度绕过第2个障碍物，最终到达目标位置.

5 结 论

针对AUV的避障与姿态控制，设计了模糊控制器，对相关公式的推导得到了控制律和自适应律，通过仿真验证了设计算法的有效性.