滇中引水工程巩树隧洞洞型分析
冯亚辉,王成言,职承杰
(1.中水北方勘测设计研究有限责任公司,天津 300202;2.长江勘测规划设计研究院,武汉 430000)
1 工程概况
滇中引水工程为Ⅰ等工程,巩树隧洞位于奔子栏~镇兰河段引水线路上,隧洞桩号为38+831~62+294,全长23463m,最大埋深为1236m。其中,进口至归达段,轴向SSW182°;归达至洛玉段,轴向SE171°;洛玉至觉挂贡段,轴向156°;觉挂贡至贡树段,轴向正S180°;贡树至出口段,轴向202°。各段之间以弧段相连。
隧洞沿线地表起伏较大,轴线地表高程2125~3300m不等,分别发育有归达、洛玉、觉挂、龙池河等较大冲沟。进口至归达段埋深浅,为54~164m,沿线地表冲沟较发育;归达至洛玉段埋深较浅,除洛玉沟埋深最浅88m外,其余埋深为268~535m;洛玉至龙池河段埋深大,除两端埋深较浅,隧洞埋深在751~1234m;龙池河至出口段埋深为120~600m,其中出口段埋深较浅,埋深多小于205m。
本次研究的泥质板岩段隧洞长度4392m,桩号41+461~45+853,占隧洞比例18.7%。洞室岩体为泥盆系下统格绒组下段(D1g1)泥质板岩,多呈微新状态,为较软岩、板理较发育,围岩为Ⅲ类。隧洞轴线与岩层走向小角度相交,易出现片帮破坏或掉块现象;另外桩号41+681、42+273发育FGS-2、FGS-3两条断层,断层带岩体较破碎,围岩为Ⅴ类。本次对不同洞型进行围岩稳定分析,提出圆形、马蹄形和城门洞型的洞型比选优化方案。
2 数值计算理论
本次分析研究采用FLAC3D软件进行数值计算。该方法是基于Cundall P.A.提出的1种显式有限差分法。FLAC方法在计算中不需通过迭代满足本构关系,只需使应力根据应力-应变关系,随应变变化而变化,因此较适合处理复杂的岩体工程问题。
2.1 运动方程
以节点为计算对象,将力和质量均集中在节点上,然后通过运动方程在时域内进行求解。节点运动方程如式(1):

将式(1)左端用中心差分来近似,则可得到:
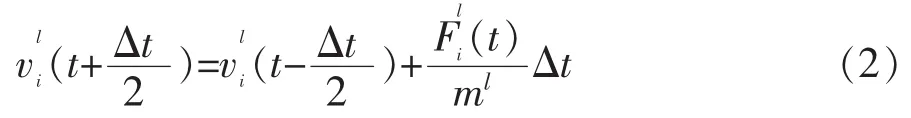
2.2 本构方程
应变速率与速度变量关系可写为:

本构关系有如下形式:

式中 k为时间历史参数;M()为本构方程形式。
2.3 应变、应力及节点不平衡力
FLAC3D由速率来求某一时步的单元应变增量,如下式:

有了应变增量,即可由本构方程求出应力增量,各时步的应力增量叠加即可得出总应力。
2.4 阻尼力
对于静态问题,在式(5)的不平衡力中加入了非黏性阻尼,以使系统的振动逐渐衰减直至达到平衡状态(即不平衡力接近零)。此时式(5)变为:

阻尼力为:
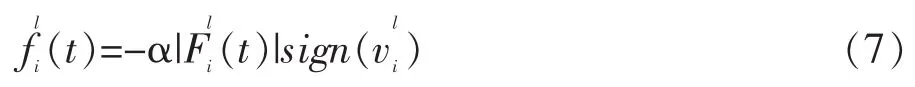
式中 α为阻尼系数。
3 初始计算条件
泥质板岩隧洞各项物理力学指标建议值的均值,作为计算采用的岩体力学参数,如表1。

表1 岩体力学参数取值
图1给出了初拟的隧洞洞型比选方案,分别为圆形断面、马蹄形断面和城门洞型断面。为方便计算对比分析,分别在每种洞型的拱顶、边墙和底板部位选定了特征点。3个洞型的比选模型,均为长×宽×高=200m×200m×200m。其中,圆形断面的计算模型共剖分155680个单元和159657个节点;马蹄形断面的计算模型共剖分154396个单元和158179个节点;城门洞型断面的计算模型共剖分了151872个单元和157662个节点。3个洞型断面计算模型,均为垂直于洞轴线方向为X向,沿洞轴线方向为Y向,Z向与铅直方向重合。计算时采用摩尔-库伦本构模型。
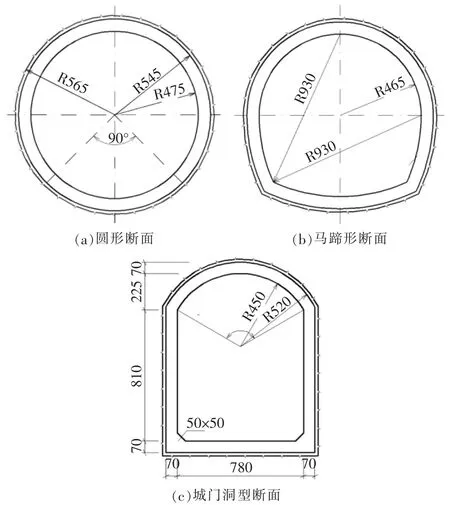
图1 对比断面示意图
4 围岩稳定分析
本次针对泥质板岩洞段,选取V类板岩力学参数和600m埋深的初始地应力选取IV类泥质板岩参数和1200m埋深的初始地应力,对比分析圆形、马蹄形和城门洞型隧洞断面的围岩稳定性,分别从围岩塑性区、塑性应变指数、形及应力4个方面进行分析。
4.1 围岩塑性区
图2给出了不同洞型条件下的塑性区分布;表2给出了不同洞型条件下洞周特征部位的塑性区深度对比;表3给出了不同洞型条件下洞周围岩的塑性区体积对比。

图2 不同洞型条件下的塑性区分布
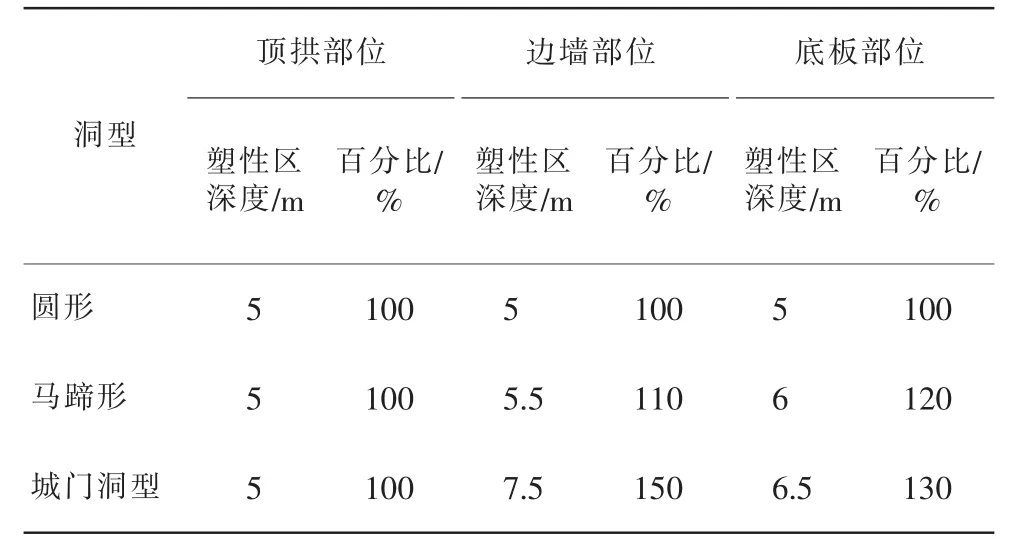
表2 不同洞型条件下洞周特征部位的塑性区深度对比
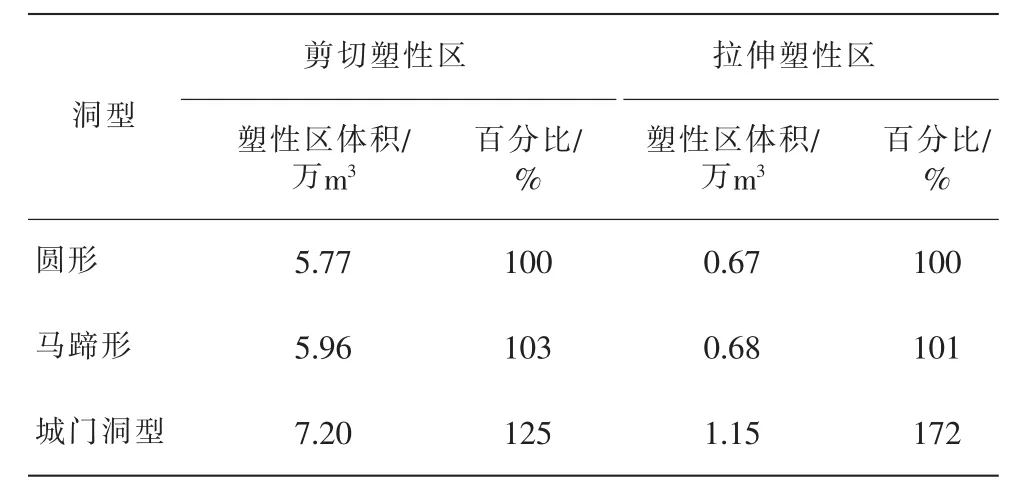
表3 不同洞型条件下洞周围岩的塑性区体积对比
(1)圆形断面的洞周各部位塑性区深度均分布在5m左右,其中剪切塑性区体积为5.77万m3,拉伸塑性区体积为0.67万m3;马蹄形断面的洞周各部位塑性区深度均分布在5~6m,顶拱部位的塑性区深度较小为5m,边墙部位稍大,为5.5m左右,底板的塑性区深度最大,为6m左右,其中剪切塑性区体积为5.96万m3,拉伸塑性区体积为0.68万m3;城门洞型断面的洞周各部位塑性区深度均分布在5~7.5m左右,顶拱部位的塑性区深度较小为5m,底板部位稍大,为6.5m左右,边墙的塑性区深度最大,为7.5m左右,其中剪切塑性区体积为7.20万m3,拉伸塑性区体积为1.15万m3。
(2)对比分析3种洞型的塑性区计算成果,圆形断面的塑性区分布范围和总体积均最小,马蹄形次之,城门洞型最大。其中,马蹄形的边墙塑性区深度为圆形的110%,底板部位的塑性区深度为圆形的120%;城门洞型的边墙塑性区深度为圆形的150%,底板部位的塑性区深度为圆形的130%。
(3)对比分析3种洞型的塑性区体积,圆形断面的塑性区体积最小,马蹄形次之,城门洞型最大。其中,马蹄形的剪切塑性区体积为圆形的103%,拉伸塑性区体积为圆形的101%;城门洞型的剪切塑性区体积为圆形的125%,拉伸塑性区体积为圆形的172%。
综合上述对比分析,可以看出,圆形断面条件下的洞周围岩塑性区深度和塑性区总体积均最小,马蹄形断面的塑性区分布范围和总体积虽然大于圆形断面,但增加的幅度较为有限,马蹄形和圆形条件下围岩塑性区分布特征相近,两种洞型条件下的围岩稳定性差别较小;城门洞型的塑性区分布范围和总体积均要显著大于圆形断面,尤其是高边墙附近的塑性区深度较大,围岩发生拉伸屈服的范围明显增加,对围岩稳定性影响显著。
4.2 围岩塑性应变指数PSI
图3给出了不同洞型条件下的塑性应变指数PSI分布,可以看出,圆形断面和马蹄形断面的洞周PSI量值基本相同,开挖面附近均在150左右,而城门洞型断面的洞周PSI量值较大,开挖面附近达到400,这表明城门洞型断面在开挖后的围岩卸荷损伤非常显著,不利于围岩稳定。
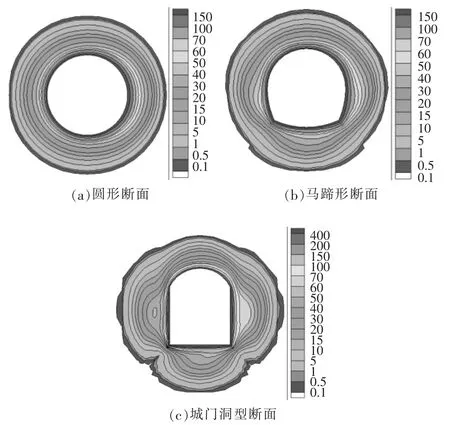
图3 不同洞型条件下的塑性应变指数PSI分布
4.3 围岩变形
图4给出了不同洞型条件下监测断面顶拱、边墙和底板监测点随掌子面推进的围岩变形,表4给出了不同洞型条件下的洞周各部位的围岩变形对比,可以看出:
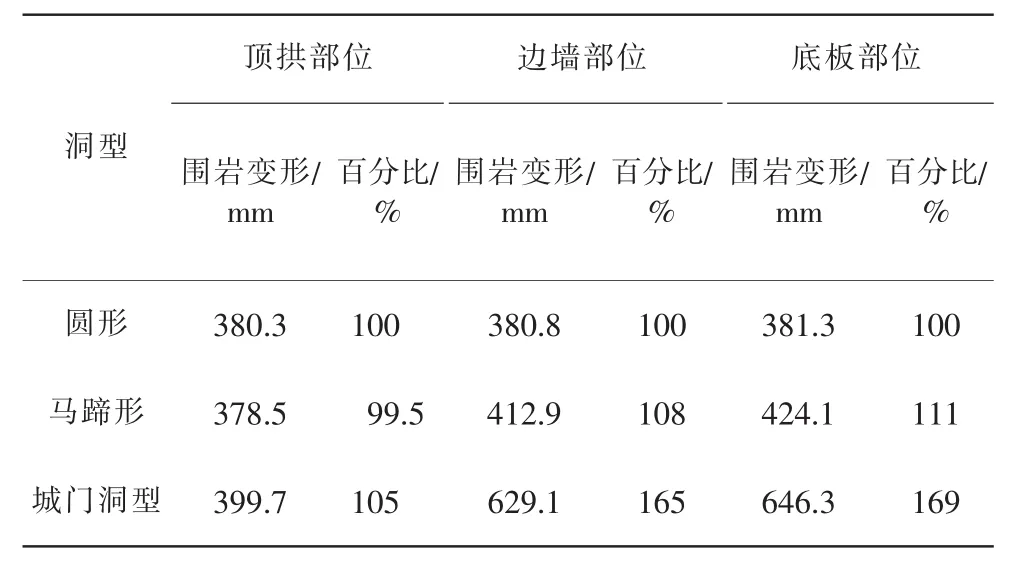
表4 不同洞型条件下洞周各部位的围岩变形对比
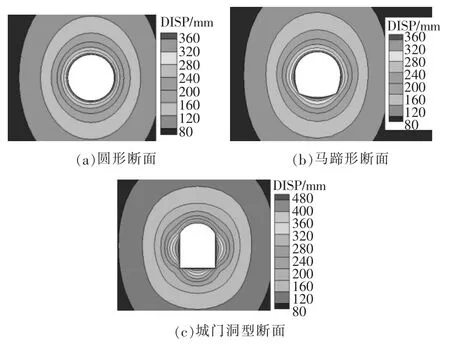
图4 不同洞型条件下的围岩变形分布特征
(1)监测断面上各监测点随掌子面推进的围岩变形变化特征。3种洞型条件下监测断面的围岩变形变化规律基本一致,均是随着掌子面不断靠近监测断面,围岩变形逐渐增长,当掌子面通过监测断面时,围岩变形增幅最为显著,当掌子面逐渐远离监测断面时,围岩变形增幅趋缓并最终趋于稳定。
(2)围岩变形分布特征。圆形和马蹄形断面的围岩变形分布均较为均匀,开挖面附近围岩没有出现局部变形明显较大的部位;城门洞型断面则在边墙和底板中部出现了较大的围岩变形,在开挖面附近的变形梯度较大。
(3)围岩变形量值。圆形断面的洞周监测点围岩变形分布在380.5~381.3mm,不同部位的围岩变形区别很小;马蹄形断面的洞周监测点围岩变形分布在378.5~424.1mm,其中顶拱部位最小,边墙次之,底板部位最大;城门洞型断面的洞周监测点围岩变形分布在399.7~646.3mm,其中顶拱部位最小,边墙次之,底板部位最大。可以看出,马蹄形断面顶拱围岩变形与圆形断面相当,边墙和底板部位的围岩变形则稍大于圆形断面,变形量值为圆形断面的99.5%~111%;城门洞型断面顶拱围岩变形与圆形断面差别较小,但在边墙和底板部位的围岩变形则要显著大于圆形断面,变形量值为圆形断面的165%~169%。这表明城门洞型断面在边墙和底板部位的变形非常显著,发生围岩变形失稳的可能性较大。
综上可以看出,圆形断面和马蹄形断面的洞型相近,不论是围岩变形分布特征还是量值均较为接近。城门洞型断面围岩的变形量值要显著大于圆形断面,尤其是边墙和底板部位的围岩变形量值较大,变形梯度也十分明显,不利于隧洞的围岩稳定。
4.4 围岩应力
图5给出了不同洞型条件下的围岩第1主应力分布,图6给出了不同洞型条件下的围岩第3主应力分布,表5给出了不同洞型条件下的洞周各部位围岩主应力对比。

表5 不同洞型条件下洞周各部位的围岩主应力对比
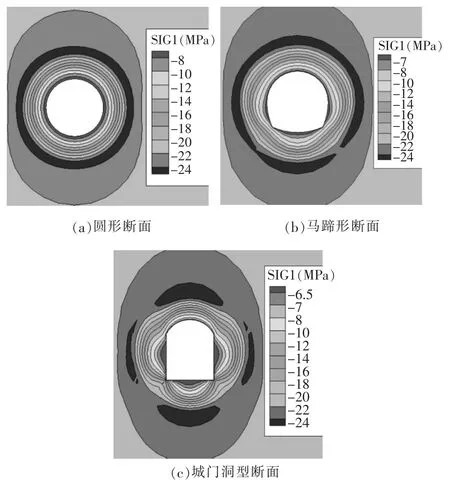
图5 不同洞型条件下的围岩第1主应力分布
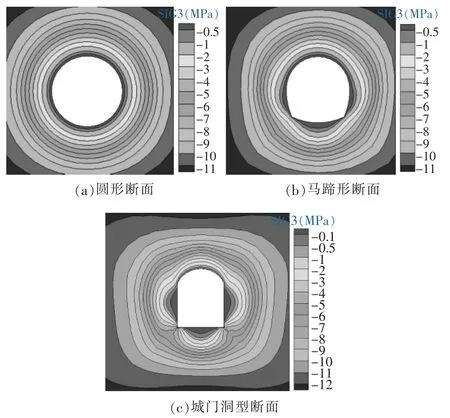
图6 不同洞型条件下的围岩第3主应力分布
可以看出圆形和马蹄形断面的洞周围岩主应力分布都较为均匀,围岩第1主应力分布在-6.6~-6.5MPa,量值差异较小。城门洞型断面的围岩在边墙和底板部位的应力量值变化较为明显,底板和边墙的交汇部位应力集中程度较为明显,第1主应力量值分布在-16~-8MPa。
5 结语
本次泥质板岩洞段隧洞,对圆形断面、马蹄形断面和城门洞型断面的围岩稳定性进行了计算分析,主要结论为:
(1)圆形断面的围岩塑性区范围和围岩变形量值均最小,围岩应力分布也较为均匀,选择圆形断面对围岩稳定性最为有利。
(2)马蹄形断面的围岩塑性区深度比圆形断面增大0.5~1m,塑性区总体积增幅在5%以内,围岩变形仅比圆形断面增大10%左右,围岩应力分布也较为均匀,选择马蹄形断面虽然围岩稳定性稍差于圆形断面,但差异不大,对围岩稳定性的影响较小。
(3)城门洞型的边墙和底板部位围岩稳定性较差,其中围岩塑性区深度比圆形断面增大0.7~2.5m,塑性区总体积增幅达30%,且边墙部位的拉伸屈服区较大;边墙和底板部位的围岩变形比圆形断面增大65%~78%,且变形梯度显著;在底板和边墙交汇部位的应力集中较为明显。相比而言,城门洞型断面的围岩稳定性最为不利,且表征围岩稳定性的各项指标均要显著差于圆形断面和马蹄形断面,发生围岩变形失稳的可能性较大。
综上,从围岩稳定性角度考虑,圆形断面最优;马蹄形断面略差于圆形断面,但差异较小;城门洞型断面最差,为保障围岩稳定,需考虑较高的支护强度。

