空间变化的二值形态算子核元的研究

段汕，张玉晓，柳倩

(中南民族大学 数学与统计学学院，武汉 430074)

数学形态学在20世纪中期由MATHERON和SERRA提出，主要利用集合、几何以及拓扑的概念对图像和信号进行分析[1]，其基本思想是利用一个称作结构元的“探针”实现对图像信息的描述和提取.形态算子的表示定理是数学形态学基础理论重要的组成部分，MATHERON通过引入核元的概念，针对形态算子建立了Matheron表示定理[2]，该定理表明所有平移不变的增性算子都可以基于算子的核元进行表示.

随着空间变化(spatially-variant，SV)形态学方法的提出，Matheron表示定理由BOUAYNAYA等人扩展到SV二值形态学的情形，并建立了SV形态算子的核表示定理[3].鉴于形态算子核表示定理具有重要的理论及实用价值[4-6]，且利用形态算子的核元可以构造等幂和自对偶形态滤波[7]，对于其构成算子表示的核元进行相关研究，不仅可以揭示核元的结构特征，而且对算子表示定理中去冗余问题也有积极的作用.

基于此，本文在平移不变二值形态学理论的基础上，对二值形态算子核元的性质进行了研究，并以此为基础，建立了SV二值形态算子核元的相关理论框架，给出在已知核元的基础上产生新核元的方法.研究结果表明：二值情况下的SV形态算子的核元保留了平移不变形态算子核元的大多数性质，此研究结果丰富了形态算子核元的理论.

1 准备工作

BOUAYNAYA等人在文献[3]中提出了SV二值形态算子的相关概念，并对其基本性质进行了研究.

在平移不变二值形态学框架中,结构元是固定不变的.将集合A沿向量x的平移记为A+x或Ax，即A+x={a+x:a∈A}.

以B为固定结构元的腐蚀和膨胀算子具有形式[9]：

基于固定结构元A,B的击中击不中算子[9]φ定义为：

φ(X)=X⊗(A,B)={x∈E:Ax⊆X⊆Bx}.

在SV二值形态学框架中,结构元是空间变化的，由θ:E→P(E)所给出的映射称为结构映射，结构映射θ的转置[3]θ′(y)={z∈E:y∈θ(z),y∈E}.

以θ为结构映射的SV腐蚀εθ(X)、膨胀δθ(X)、开Γθ(X)、闭Φθ(X)定义[3]为：

基于结构映射θ1,θ2的击中击不中算子[5]φ定义为：

φ(X)=X⊗(θ1,θ2)={z∈E:θ1(z)⊆X⊆θ2(z)}.

(1)

上述算子具有如下性质[5]：

εθ(X)⊆X⊆δθ(X)；

(2)Γθ(X)⊆X⊆Φθ(X).

2 平移不变核元的基本性质

依据文献[9],算子α的平移不变核K(α)定义为：K(α)={A:0∈α(A)}.

利用平移不变形态算子的基础知识，对于平移不变核K(α)不难建立以下性质：

性质1设X,A,B∈P(E)，则有：

(2)对于平移不变算子α1,α2，α1≤α2的充要条件是：K(α1)⊆K(α2).

(3)对于算子α1,α2，有K(α1∨α2)=K(α1)∪K(α2);K(α1∧α2)=K(α1)∩K(α2).

(4)设α为增性算子，A⊆B，若A∈K(α)，则

B∈K(α).

(5)若α为增性自对偶算子，σ=id∧αv，则

A∈K(σ)的充要条件是：Ac∈K(α)且0∈A.

(8)[11]若φ(X)=X⊗(A,B)，则：

1)K(φ)=[A,B]，其中，[A,B]表示闭区间，即[A,B]={X:A⊆X⊆B}；

运用以上形态算子核元的基本性质，可以进一步研究SV二值形态算子核元的相关性质.

3 SV核元的性质

算子α的SV核[3]Ker(α)定义为：

(2)

3.1 SV核元的一般性质

性质2[5]设α1,α2∈O，则α1≤α2的充要条件是：Ker(α1)⊆Ker(α2).

性质3对于α1,α2∈O，有：

(1)Ker(α1∨α2)⊇Ker(α1)∪Ker(α2)；

(2)Ker(α1∧α2)=Ker(α1)∩Ker(α2).

证明(1)若θ∈Ker(α1)∪Ker(α2)，则θ∈Ker(α1)或θ∈Ker(α2)，由SV核的定义(2)式，则对于任意的z∈E，有z∈α1(θ(z))∪α2(θ(z))=(α1∨α2)(θ(z))，所以θ∈Ker(α1∨α2)，故Ker(α1)∪Ker(α2)⊆Ker(α1∨α2).

Ker(α2).

性质4θ∈Ker(α)的充要条件是：θc∈Ker(αv)，其中θc(z)=(θ(z))c,z∈E.

证明充分性：由θc∈Ker(αv)，则对于任意的z∈E，有z∈α(v(θc(z)))=α((θc(z))c)=α(θ(z)),故θ∈Ker(α).

必要性：由θ∈Ker(α)，则对于任意的z∈E，有

z∈α(θ(z))=α((θc(z))c)=α(v(θc(z))),故θc∈Ker(αv).

3.2 增性算子的SV核元的性质

性质5设α∈O是增性算子，θ1≤θ2，若θ1∈Ker(α)，则θ2∈Ker(α).

证明若θ1∈Ker(α)，则对于任意的z∈E，有z∈α(θ1(z))，又α是增性算子且θ1≤θ2，所以有z∈α(θ1(z))⊆α(θ2(z))，于是有z∈α(θ2(z))，故θ2∈Ker(α).

性质6设α∈O为增性算子，若θ1∈Ker(α),θ2∈Ker(α*)，则对于任意的z∈E，θ1(z)∩

由上述性质可以得到以下推论:

性质7对于结构映射θ,θ1，有

(1)θ∈Ker(εθ1)的充要条件是：θ1≤θ；

证明(1)充分性：由θ1≤θ，则对于任意的z∈E，θ1(z)⊆θ(z)，于是有z∈{z0∈E:θ1(z0)⊆θ(z)}=εθ1((θ(z))，故θ∈Ker(εθ1).

必要性：由θ∈Ker(εθ1)知，对于任意的z∈E，有z∈εθ1((θ(z))={z0∈E:θ1(z0)⊆θ(z)}，从而有θ1(z)⊆θ(z)，即θ1≤θ.

3.3 转换算子的SV核元的性质

性质8若α∈O为增性自对偶算子，σ为与α相关的转换算子，则θ∈Ker(σ)的充要条件是：对于任意的z∈E,z∈θ(z)且z∈α(θc(z)).

θ∈Ker(id)∩Ker(αv)=Ker(id∧αv)=Ker(σ).

3.4 击中击不中算子的SV核元的性质

对于(1)式所定义的击中击不中算子φ，用[θ1,θ2]表示如下映射段：[θ1,θ2]={θ:θ1≤θ≤θ2}，则有以下性质成立：

性质9Ker(φ)=[θ1,θ2].

证明对于θ∈Ker(φ)，有任意的z∈E,z∈φ(θ(z))={z0∈E:θ1(z0)⊆θ(z)∈θ2(z0)},

所以有θ1(z)⊆θ(z)⊆θ2(z)，即θ∈{θ0:θ1≤θ0≤θ2}=[θ1,θ2]，于是有Ker(φ)⊆[θ1,θ2]，同理，对于θ∈[θ1,θ2]，有任意的z∈E，θ1(z)⊆θ(z)⊆θ2(z)，所以z∈{z0∈E:θ1(z0)⊆θ(z)⊆θ2(z0)}=φ(θ(z))，即θ∈Ker(φ)，于是有[θ1,θ2]⊆Ker(φ)，因此可得Ker(φ)=[θ1,θ2].

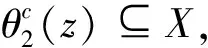
4 SV核元的产生

可以通过对已知的SV核元进行极大、极小运算、腐蚀、膨胀、开和闭以及平移运算产生新的核元.

性质11对于θ1,θ2∈Ker(α),有

(1)若α关于集合的交运算可交换，则θ1∧

θ2∈Ker(α)；

(2)若α关于集合的并运算可交换，则θ1∨

θ2∈Ker(α).

证明(1)若α关于集合的交运算可交换，由条件θ1,θ2∈Ker(α)，则对于任意的z∈E,有z∈α(θ1(z))∩α(θ2(z))=α((θ1∧θ2)(z))，于是，有z∈α((θ1∧θ2(z))，故θ1∧θ2∈Ker(α).

(2)若α关于集合的并运算可交换，由条件θ1,θ2∈Ker(α)，则对于任意的z∈E，有z∈α(θ1(z))∩α(θ2(z))⊆α(θ1(z))∪α(θ2(z))=α((θ1∨θ2)(z))，于是，有z∈α((θ1∨θ2)(z))，故θ1∨θ2∈Ker(α).

给定两个结构映射θ和θ1，用εθ1(θ),δθ1(θ),Γθ1(θ),Φθ1(θ)来表示结构映射的SV腐蚀、膨胀、开和闭，即对任意的z∈E,(εθ1(θ))(z)=εθ1(θ(z)),(δθ1(θ))(z)=δθ1(θ(z)),(Γθ1(θ))(z)=Γθ1(θ(z)),(Φθ1(θ))(z)=Φθ1(θ(z)).在此基础上，可以通过对结构元θ进行SV腐蚀、膨胀、开和闭运算来产生SV核元.

性质12对于θ∈Ker(α)及结构映射θ1，有

(3)若α是减性算子，则Γθ1(θ)∈Ker(α)；

(4)若α是增性算子，则Φθ1(θ)∈Ker(α).

证明(1)由θ∈Ker(α)，则对于任意的z∈E，有z∈α(θ(z))，所以由SV腐蚀的性质及α是减性算子可得：z∈α(θ(z))⊆α(εθ1(θ(z)))，于是z∈α(εθ1(θ(z)))=α((εθ1(θ))(z))，故δθ1(θ)∈Ker(α).

(2)由θ∈Ker(α)，则对于任意的z∈E，有z∈α(θ(z))，所以由SV膨胀的性质及α是增性算子可得：z∈α(θ(z))⊆α(δθ1(θ(z)))，于是有z∈α(δθ1(θ(z)))=α((δθ1(θ))(z))，故δθ1(θ)∈Ker(α).

同理可证得(3)、(4).

给定结构映射θ，用θa表示映射θ通过元素a∈E的平移，即对于任意的z∈E，θa(z)=(θ(z))a，则可以通过对结构映射θ进行平移运算来产生SV核元.

性质13若α为平移不变算子，则θa∈Ker(α)(a∈E)的充要条件是：对于任意的z∈E,(θ(z))a-z∈K(α).

给定结构映射θ和固定结构元B，建立新的结构映射θΘB，θ⊕B，其定义为：

(θΘB)(z)=θ(z)ΘB，(θ⊕B)(z)=θ(z)⊕B.

性质14设α为平移不变算子，

(1)若α关于集合的交运算可交换，则θΘB∈Ker(α)的充要条件是：对于任意的z∈E，任意的b∈B,θ-b-z∈K(α)；

(2)若α关于集合的并运算可交换，则θ⊕B∈Ker(α)的充要条件是：对于任意的z∈E，存在b∈B，使得θb-z∈K(α).

上述研究表明，SV形态算子的核元与平移不变形态算子核元的性质基本保持一致.

5 结语

本文在已有文献的基础上，对平移不变二值形态算子核元的性质进行了研究，实现了从平移不变形态算子核元到SV形态算子核元研究的扩展，并在已知核元的基础上研究了产生新核元的几种方法，丰富了形态算子核元的理论成果.后续可以进一步研究灰值形态算子核元的性质以及形态算子核元的应用，从而使此研究工作更加完善.