雄安新区长历时暴雨强度公式及其设计雨型推求

于长文 许启慧 杨宜昌 马贵东 高旭旭

(河北省气候中心，河北 石家庄 050021)

引言

在全球气候变化和中国高速城市化发展的背景下，暴雨洪涝、城市内涝灾害更加严重[1]，利用分钟级气象观测数据开展分区暴雨强度公式编制和设计暴雨雨型，已成为适应气候变化的城市规划中的一项重要内容[2]。设计暴雨的研究是现代城市排水工程设计的基础，对确定城市排水工程设计规模与投资具有重要影响[3]。城市设计暴雨主要包含编制城市暴雨强度公式和设计暴雨雨型[4]两部分内容，长期以来，城市暴雨强度公式指历时小于180 min的暴雨公式，亦称短历时暴雨强度公式，近年来国内已有较多研究成果[5-7]，而关于长历时设计暴雨的研究，主要集中在利用频率曲线推算设计暴雨量[8-10]，该设计雨量是在建立暴雨强度公式前期，对样本数据进行外延以获得重现期远超出实测资料年限的雨量设计值，与暴雨强度公式的计算值存在差异，不建议直接进行推广应用。在暴雨雨型设计方面，对小于180 min的短历时暴雨雨型主要采用《城市暴雨强度公式编制和设计暴雨雨型确定技术导则》[11](以下简称《导则》)中推荐的芝加哥法雨型[12-14]，统计综合雨峰位置系数，最终确定设计暴雨的时间变化过程。我国大部分地区在推求长历时设计暴雨雨型时，多采用选取典型暴雨过程，进行同倍比或同频率分时段控制缩放[15-17]，设计降雨历时通常不会超过24 h[18]，即1440 min。目前，同频率分析法是研究1440 min设计暴雨雨型较为成熟的方法，被广泛应用于城市长历时设计暴雨雨型的研究中。同频率分析法是基于最小分钟步长，统计每个步长中降雨量在其整个降雨过程中所占的比例，最终获得的是雨量时程分配比例值，还需通过暴雨强度公式计算出不同重现期各历时的设计雨量值，将其带入分配比例，最终得到长历时设计暴雨雨型。由此可见，对于1440 min设计暴雨雨型的获得，除了降雨结构，还需编制长历时暴雨强度公式，来完成设计雨量值的求解。

雄安新区的设立是千年大计、国家大事，承载着京津冀协同优化发展的历史重任，是新时代探索人类高质量发展的未来之城[19]。雄安新区地处海河流域大清河水系缓洪滞沥地区，九河下梢的低洼平原，地形开阔，水系密集，易发生暴雨洪涝灾害[20]。因此，在雄安新区建设蓝图布局伊始，有必要对当地的降雨特征进行分析，对区域内的设计暴雨进行研究，编制出该地适用于不同重现期、不同历时的综合暴雨强度公式，推求设计暴雨量随时间的变化过程，即设计暴雨雨型[21-22]，以期为雄安新区城市管网排水与区域洪涝灾害防御布局的规划设计提供可靠的基础数据支撑，对保障新区城市安全、海绵城市建设、塑造高品质宜居环境等方面具有重要的现实意义。

1 资料与方法

1.1 数据来源及处理

1.1.1 降雨特征分析数据

按照气象部门标准，本文将日降雨量≥50 mm记为一个暴雨日，将日降雨量≥100 mm记为一个大暴雨日。雄安新区内有容城(115.82°E，39.07°N，海拔高度为12.8 m)、安新(115.93°E，38.93°N，海拔高度为4.4 m)和雄县(116.12°E，39.02°N，海拔高度为10.3 m)3个地面气象观测站，其降雨量和日数的分析采用辖区内上述3个气象观测站的平均值进行统计，起止时间为1981—2020年共40 a，数据来自河北省气象信息中心。

1.1.2 分钟降雨数据

对容城、安新和雄县近40 a的降雨量、暴雨日数的对比分析可知，无论是降雨量还是暴雨日数，均为雄县最大，而且雄县气象站也是3个站中最早启用自动站单轨运行的台站(2010年，其他2站为2012年)，因此本文以雄县气象站为例，进行长历时综合暴雨强度公式的推求和设计暴雨雨型的研究。选取雄县气象站1981—2020年逐分钟降雨数据，其中1981—2004年的数据为自记纸观测，使用前通过“降水自记纸彩色扫描数字化处理系统”[23]对其进行了信息化处理，并做了审核和校验。2004年以后为新型自动气象站记录的逐分钟雨量数据。

1.2 研究方法

1.2.1 长历时综合暴雨强度公式的推求

1.2.1.1 暴雨选样

编制暴雨强度公式之前，需要对降雨数据进行选样，方法通常包括年最大值法和非年最大值法两类。根据《室外排水设计规范》(GB50014—2006，2016版，以下简称《规范》)要求[24]，年最大值法选样采用的气象观测资料年限在30 a以上，短历时暴雨雨型设计采用的资料要求亦是如此；而《导则》中明确指出，城市暴雨强度公式的编制应采用年最大值法，当样本中存在稀遇暴雨值时，应合理取舍。

在对雄县气象站分钟降雨数据进行质量控制时发现，1991年的720 min和1440 min的降雨样本数据中，存在极端特大值，该数值超出计入特大值后均值的3倍，当将其纳入理论频率曲线拟合时，该值较本地500年一遇的暴雨设计值还大，因此将其删除。最终选取1981—2020年(无1991年)共39 a的分钟降雨数据，分别以所选历时为步长，滑动选取5 min、10 min、15 min、20 min、30 min、45 min、60 min、90 min、120 min、150 min、180 min、240 min、360 min、720 min和1440 min共15个历时的逐年最大值，作为“年最大值法”选样的数据。

1.2.1.2 频率曲线分析

从概率的意义来看，暴雨属于一种随机事件，关于暴雨频率到底符合哪种分布线型，尚无统一认识[25]。由于本研究编制的暴雨强度公式是涵盖180 min以上降雨历时的综合公式，为兼顾长、短历时降雨样本的拟合优度[26-28]，最终选用P-III(Pearson-Ⅲ)型曲线对降雨数据进行频率分析，其概率密度函数为：

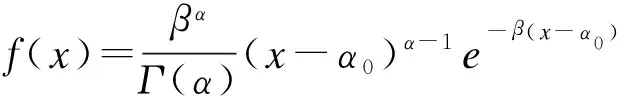
(1)

式(1)中，Γ(α)为伽马函数，α、β、α0分别为P-III型分布的形状、尺度和位置参数，详细表达式可参见《导则》附录C。求指定频率P的设计值xp为：

(2)

(3)

1.2.1.3 暴雨强度公式的型式与参数确定

不同的国家和地区采用的城市暴雨强度公式有所差异，公式的型式是编制过程中一个比较关键的问题，目前我国常用的四参数城市暴雨强度公式型式为[29]：

(4)

式(4)中，i为设计暴雨强度(单位为mm/min)，T为重现期(单位为a)，取值范围为2—100 a；t为降雨历时(单位为min)，取值范围为5—1440 min；A1、C、b、n是与地方暴雨特性有关且需要求解的参数。暴雨强度公式是一个超定非线性模型，本文基于MATLAB的高斯—牛顿法求解其参数[30]。

1.2.1.4 精度检验

精度检验分为两个阶段。第一阶段为频率拟合的精度检验，即P-III频率分布的拟合值与原始数据的误差，第二阶段为暴雨强度公式计算值与频率分布拟合值的误差，即公式计算值与T-t-i三联表中设计雨强的值。具体误差的计算公式如下：

频率拟合的平均绝对均方误差：

(5)

频率拟合的平均相对均方误差：

(6)

暴雨强度公式的平均绝对均方误差：

(7)

暴雨强度公式的平均相对均方误差：

(8)

式(5)—式(8)中，R′为频率曲线拟合暴雨量值，R为原始暴雨量值，单位均为mm；q为暴雨强度公式计算的理论暴雨强度值，q′为T-t-i三联表中的设计暴雨强度值，二者单位均为mm/min。m为历时的个数，m0为重现期。

1.2.2 同频率分析法

同频率分析法是指长降雨历时包含短降雨历时雨型，亦称“长包短”[31]，具体操作步骤如下：

(1)首先要确定雨峰位置，挑选最具有代表性的降雨过程的雨峰位置为主峰；

(2)移动所选的多场降雨过程，使其主峰对齐，在对应的位置上截取1440 min降雨过程，以5 min为统计单位，相当于288个5 min的降雨量；

(3)分别求各场降雨5 min对应位置上的分配比例，然后不分场次，求出多场降雨相同位置处、每5 min比例的平均值，总共有288个平均值；

(4)在288个平均值中找到连续的、最大的144个数的和的位置，将剩余的144个数的系列作为单位1进行各段比例分配，从而得到1440—720 min时段的分配比例；

(5)根据上述步骤依次类推，可分别求出720—360 min、360—240 min、240—180 min、180—150 min、150—120 min、120—90 min、90—60 min、60—45 min、45—30 min、30—15 min和5 min的分配比例；

(6)通过城市长历时暴雨强度公式求不同重现期各历时的设计雨量值，将其带入最终的分配比例，即可得到所需重现期下历时1440 min的设计暴雨量时程分配结果，即设计雨型。

2 结果分析

2.1 雄安新区降雨的时间变化特征

2.1.1 降雨量及暴雨日数的年内分布

1981—2020年，雄安新区多年平均降雨量为490.4 mm，其中6—9月各月的降雨量均在50 mm以上，累计降雨量占全年降雨量的78.0%。全年5—10月可监测到暴雨天气，夏季的7月和8月为暴雨的多发时段，7月多年平均暴雨日数为2.1 d，占全年的46.6%(图1)。

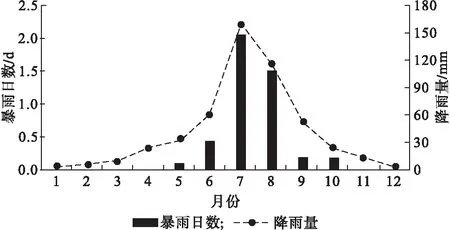
图1 1981—2020年雄安新区累年各月平均降雨量和暴雨日数变化Fig.1 Variation of monthly averaged precipitation and the number of storm days from 1981 to 2020 in Xiong′an New District

2.1.2 暴雨日数的历年变化

1981—2020年，雄安新区多年平均暴雨日数为4.4 d，年暴雨日数整体波动较大(图2)，其中1994年13 d，为历年最多，1999年0 d为历年最少；从9 a滑动平均曲线来看，暴雨日呈“升—降—升”的起伏形态，2000—2020年整体呈增多趋势，期间大暴雨的发生日数占主要贡献，这一统计结果也反映出本地区降雨极端性的增强。

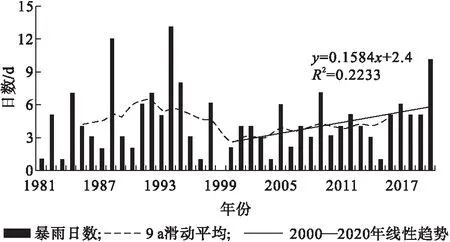
图2 1981—2020年雄安新区历年暴雨日数变化Fig.2 Variation of the number of storm days from 1981 to 2020 in Xiong′an New District

图3为不同年代大暴雨发生日数占暴雨日数的比率，由图3可见，近10 a(2011—2020年)大暴雨发生日数占比最多，达20.8%，其他各年代均不到10%，这个结果比最少的21世纪初10 a(2001—2010年)大将近7倍。2016年，该地区发生大暴雨日4 d，为近40 a最多。

图3 1981—2020年雄安新区大暴雨日数占暴雨发生日数的比率Fig.3 Proportion of the number of torrential rain days to storm days from 1981 to 2020 in Xiong′an New District

2.2 长历时暴雨强度公式推求

2.2.1 频率曲线拟合分析

基于P-Ⅲ型频率分布曲线调整选样数据资料，固定每个历时的Cs/Cv=3.5，调整各个参数使曲线拟合最优，并保证15个历时的频率拟合曲线为一簇互不相交的平行曲线(图4)，具体参数及误差检验结果如表1所示。曲线拟合值与原样本数据之间的平均绝对均方误差随降雨历时增大而减小，60 min及以上历时平均绝对均方误差均在0.055 mm/min以下。大部分历时的平均相对均方误差在10%以内。表2为重现期2—100 a间的重现期—历时—雨强表，即T-t-i三联表，由表2可见，同一重现期下，雨强随历时增大而减小，同一历时雨强随重现期增大而增大。

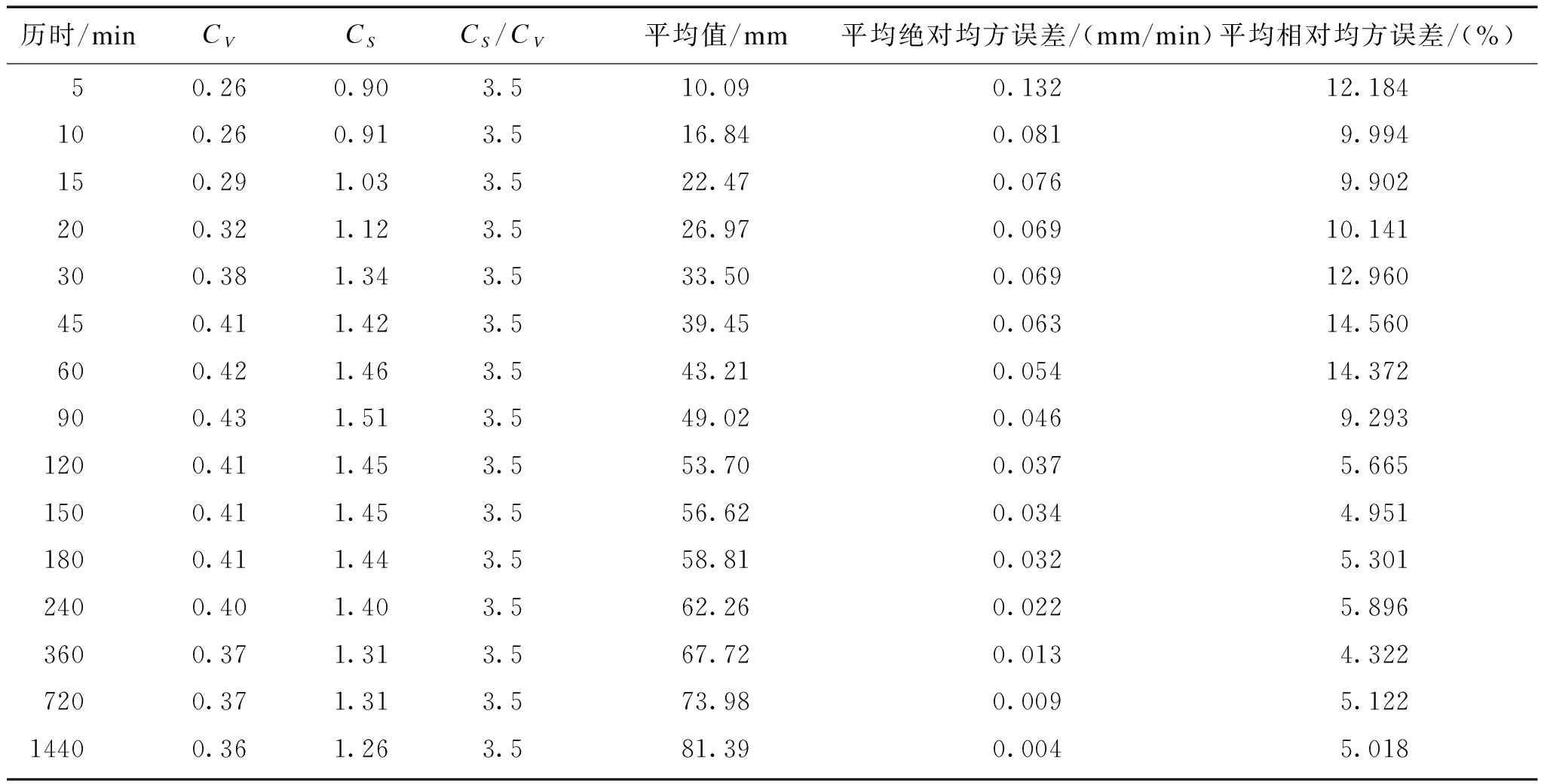
表1 基于1981—2020年雄县降雨数据进行P-III分布曲线拟合的参数值Table 1 Parameters of P-Ⅲ curve fitting of annual maximum rainstorm of different durations in Xiong country from 1981 to 2020

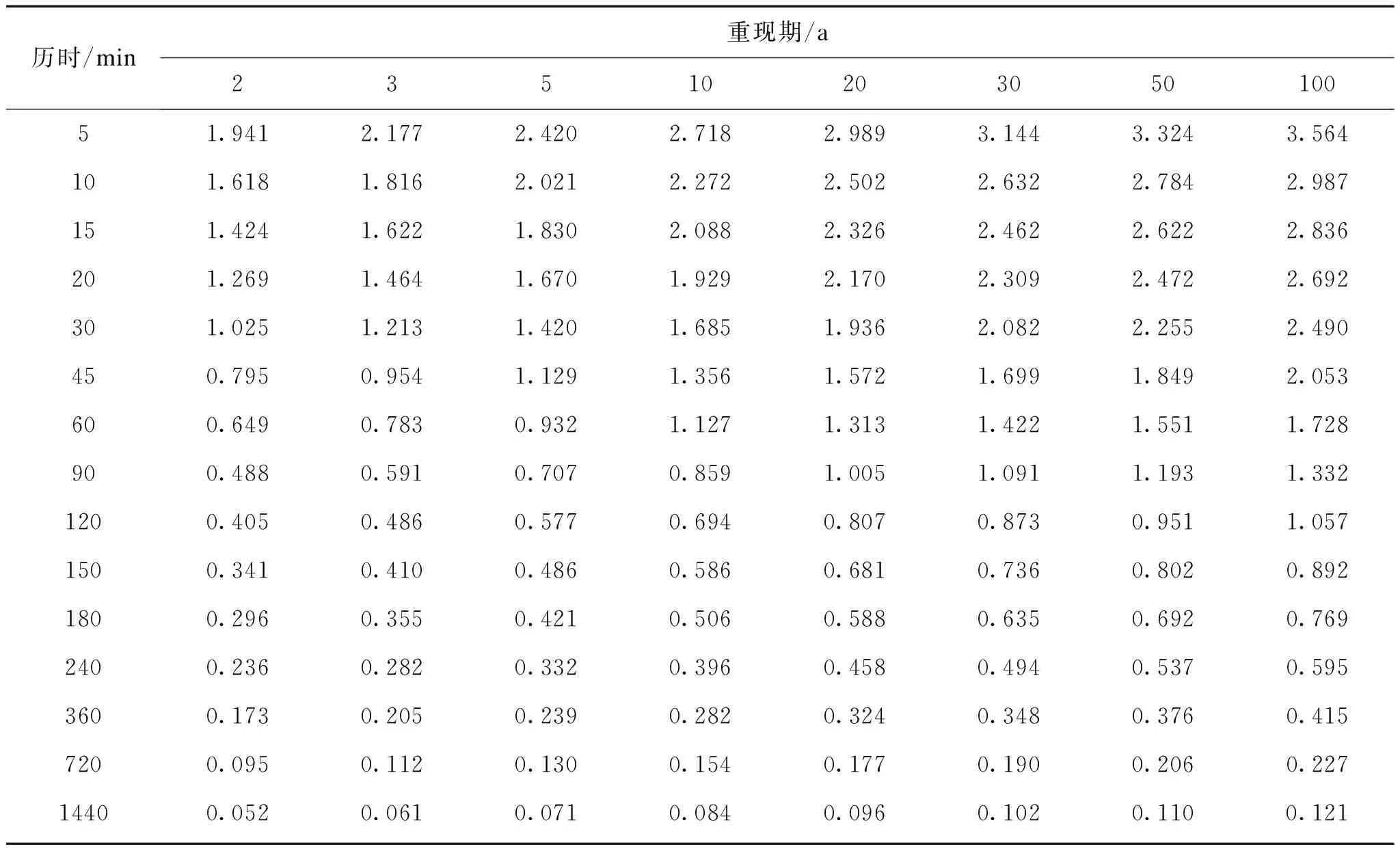
表2 雄县P-Ⅲ分布的重现期—历时—雨强表Table 2 Lasting period and its corresponding rainfall intensity for different recurrence periods of P-Ⅲ mm/min

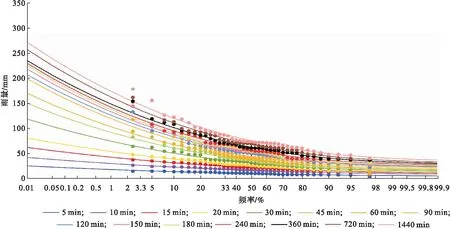
图4 1981—2020年雄县不同历时年最大降雨量P-Ⅲ分布曲线Fig.4 P-Ⅲ curve fitting of annual maximum rainstorm of different durations from 1981 to 2020 in Xiong country

2.2.2 长历时综合暴雨强度公式结果及精度检验

通过MATLAB的高斯—牛顿法求解暴雨强度式(4)中的各参数，结果得到A1=42.189，C=0.893，b=32.599，n=0.948，带入参数，即可得到雄县长历时综合暴雨强度公式：

(9)

式(9)的适用范围为：5 min≤t≤1440 min，2 a≤T≤100 a。为保证暴雨强度公式计算结果的准确性，需对其进行精度检验。对于时长小于180 min的短历时暴雨强度公式，《导则》及《规范》[24]中都要求，在采用“年最大值法”选样时，需计算重现期2—20 a区间的平均绝对均方误差和平均相对均方误差，衡量标准是以平均绝对均方误差小于0.05 mm/min，对应降雨强度较大的地区，也可采用平均相对均方误差≤5%的标准。

本文根据式(7)和式(8)计算所推求的长历时综合暴雨强度公式(9)的精度，具体结果列于表3。由表3可见，在重现期为2—100 a区间，20 min、120 min及以上历时共8个历时的绝对误差在0.05 mm/min以下，15个历时的整体平均绝对误差为0.064 mm/min，平均相对误差为5.258%；在重现期为2—20 a区间，15 min、20 min、60 min及以上历时共12个历时的绝对误差在0.053 mm/min以下，15个历时的整体平均绝对误差为0.048 mm/min，平均相对误差为5.34%。显然重现期为2—20 a区间的误差结果满足相关规定的要求，由此进一步证明了所编制的长历时综合暴雨强度公式的可靠性。

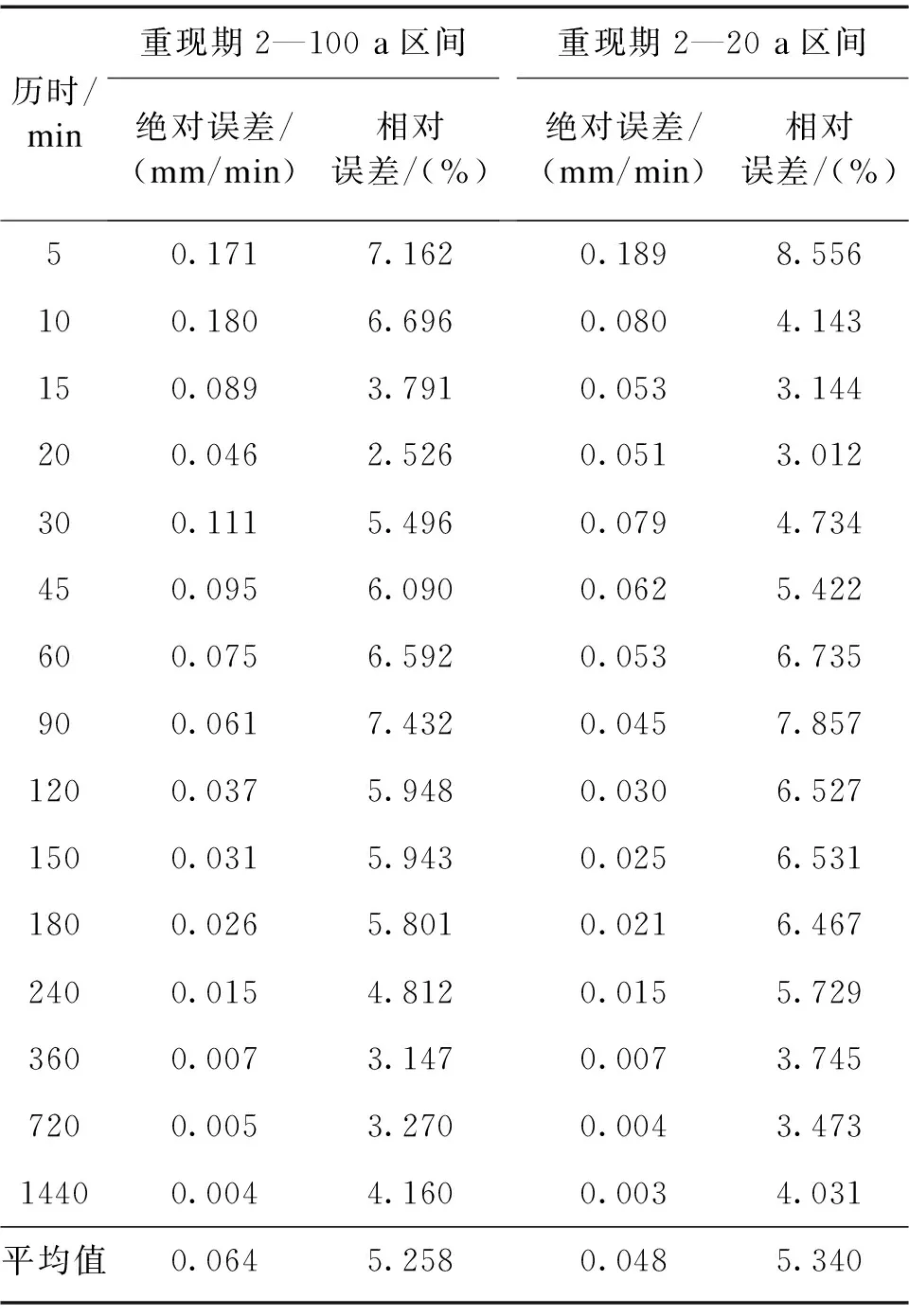
表3 雄县长历时综合暴雨强度公式的误差检验结果Table 3 Error test of the long-duration comprehensive storm intensity formula in Xiong county

2.3 历时1440 min设计暴雨雨型

同频率分析法所需要的典型降雨过程应具有明显的致灾特征，一般具有雨量大而集中、雨峰相对靠后的特点[17]。集中度越高，雨峰系数越大，积水总量的峰值越大，同一重现期下，雨峰系数越大，积水面积越大[32]，造成的灾害也就会越严重。表4为雄县在1981—2020年所选的12场典型暴雨过程，由表4可见，发生于20世纪90年代的有4场，2000年之后的有4场，其中1991年7月27日发生的特大暴雨，其日雨量为近40 a最大，发生于2007年7月30日的特大暴雨，其最大1 h雨强达80 mm以上，为所选典型暴雨过程中最大。

表4 1981—2020年雄县典型暴雨过程概况Table 4 Overview of the typical storm in Xiong conty from 1981 to 2020

根据前文同频率分析法推求长历时设计暴雨雨型的步骤，对表4的暴雨过程进行设计雨型分析，最终得到以5 min为步长历时1440 min设计暴雨雨型，如图5所示。雄县1440 min设计暴雨雨型为典型的单峰型，雨峰处于第232时段，即1160 min处，雨峰系数为0.806，峰值位置靠后，落后于整场降雨过程的2/3分位。

图5 基于1981—2020年降雨数据推求出的雄县以5 min为步长1440 min设计暴雨雨型Fig.5 The design hyetograph of 1440 min with an interval of 5 min in Xiong county base on precipitaion data from 1981 to 2020

根据式(9)长历时综合暴雨强度公式求得的雨量值分别对应带入最终分配比例，可得到指定重现期下1440 min的设计暴雨时程分配，即雨型。图6为重现期100 a的结果，分析可知，雄县重现期100 a历时1440 min的设计暴雨雨型为单峰型，雨峰时段的平均降雨强度为3.78 mm/min，在1—225时段，降雨量增加缓慢，时段降雨量均低于2 mm，累积降雨量为44.46 mm，第226—232时段，降雨量迅速增大，第232时段达到峰值，为18.9 mm/(5 min)，此时累积降雨量接近100 mm；第233—244时段，时段降雨量由14.3 mm/(5 min)快速减弱至0.66 mm/(5 min)，第245—288时段基本低于0.5 mm，此时雄县100 a重现期历时1440 min的累积降雨量达168.38 mm(图6b)。

图6 100 a重现期1440 min设计暴雨雨型(a)及累积降雨量(b)Fig.6 The design storm hyetograph (a) and accumulative rainfall (b) of 1440 min for recurrence period of 100 years

3 结论与讨论

(1)近40 a，雄安新区平均降雨量为490.4 mm，暴雨日数为4.4 d，降雨主要集中在6—9月，5—10月可监测到暴雨天气，7—8月为暴雨的多发时段，其中7月最多，占全年的46.6%；2000—2020年，暴雨日数整体呈增多趋势，期间大暴雨的发生日数增多明显，这一统计结果也反映出本地区降雨极端性的增强。2011—2020年，雄安新区大暴雨发生日数占比最多，达20.8%，较最少的21世纪初10 a(2001—2010年)大将近7倍。

(2)以雄县为例，采用年最大值法选样，为兼顾长、短历时降雨样本的拟合优度，选用P-III型曲线对降雨数据进行理论频率分析，通过MATLAB的高斯—牛顿法求解暴雨强度公式中的参数，最终得到适用于5—1440 min的长历时综合暴雨强度公式，其精度检验结果表明，2—100 a重现期内，15个历时的整体平均绝对误差为0.064 mm/min，平均相对误差为5.268%；2—20 a重现期内，15个历时的整体平均绝对误差为0.048 mm/min，平均相对误差为5.348%。公式的整体误差结果基本满足相关规定的要求，由此进一步证明了所编制公式的可靠性。

(3)利用同频率分析法得到雄县以5 min为步长，历时1440 min的设计暴雨雨型为单峰型，其峰值在第232时段，雨峰系数为0.806，落后于整场降雨过程的2/3分位。结合所编制的长历时综合暴雨强度公式，可计算出任意指定重现期下1440 min降雨过程的雨量时程分布。

城市化与气候变化是未来人类社会面临的两大挑战，二者的联系也日益紧密，在气候变化的大背景下，降水也随之发生变化[33]。为适应城市化、生态文明建设、防灾减灾和应对气候变化等，开展城市水文气象方面的科学研究与应用十分必要。雄安新区规划建设面临从农村到城市的巨大转变，新区的快速建设将使得下垫面产汇流特征发生显著变化，设计暴雨的差异将导致径流计算结果的不同，对峰值流量(尤其是硬化地面)有决定性影响。本文仅以雄县为例，对24 h及其以内的暴雨强度设计值进行了推求，后续将开展容城和安新的长历时综合暴雨强度公式及其设计雨型的研究，以期为新区的工程建设提供更加精准的科技支撑。