鄱阳湖地区零平面位移及动力粗糙度的计算

饶志娟 朱彬 汪如良 刘熙明

(1.江西省气象学会秘书处，江西 南昌 330096； 2.南京信息工程大学环境科学与工程学院，江苏 南京 210044；3.南京信息工程大学大气物理学院，江苏 南京 210044； 4.江西省气象服务中心，江西 南昌 330096；5.江西省气象科学研究所，江西 南昌 330096)

引言

大气边界层是人类生产、生活的主要空间，人类活动通过改变自然地表特征影响边界层内大气湍流运动，并对天气气候产生影响[1]。地表类型复杂且非均匀的下垫面不仅使得边界层湍流运动多变，而且对数值模式的模拟能力提出了挑战。各类大气模式的模拟效果不仅取决于气象探测数据的精度还取决于对下垫面性质的了解和湍流特征量的表征。

空气动力学粗糙度是大气边界层的一个重要概念，反映了地表状态的物理特性。空气动力粗糙度最早由Bagnold[2]提出，他通过大量的风洞实验研究气流与沙粒的相互作用，并得到了著名的空气动力粗糙度1/3定律。早期的研究基本集中在农田、海面、森林或城郊等起伏不太大的下表面[3-4]，Baldauf等[5]在中性层结和地形平坦的条件下，对任意给定的粗糙度分布z0(x，y)，提出了一种参数化的有效粗糙度长度计算方法，他考虑了空间结构分布，尤其是长度尺度的影响和气流流入的方向。近年来开展的复杂地形大气湍流结构的研究更具有现实意义。Zhong等[6]在陆面模式中发展了一种计算非均匀地表的有效粗糙度和零平面位移的新方案。黄鹤等[7]研究了渤海西岸空气动力学粗糙度特征，对比分析了风廓线法和风速标准差法的计算结果。沙敏敏等[8]利用多层风速、风向观测资料计算了北京市空气动力学粗糙度，发现地表粗糙度、零平面位移随着城市化发展皆有明显增加的趋势。

鄱阳湖是我国第一大淡水湖，是国际重要湿地，湖区呈盆状凹地，周边地形亦复杂，具有典型的非均匀下垫面特征。研究鄱阳湖地区非均匀下垫面地表粗糙度特征，对于局地天气预报、湖滨地区风能资源利用、空气污染物扩散、边界层特征数值模拟等具有重要意义[9-10]。本文利用2013年7月1日至2014年6月30日鄱阳湖东岸70 m铁塔涡动相关观测资料，计算零平面位移及粗糙度，并为本地化陆面模式提供参考，以期提高模式输出效果和预报准确性。

1 资料与方法

70 m观测塔位于鄱阳湖东岸的江西省鄱阳县白沙洲乡境内(29.16°N，116.61°E)，距离鄱阳县气象基准站18.0 km，铁塔周边地形平坦，下垫面主要为低矮灌木。观验采用的EC150开路涡动相关观测仪安装在铁塔44.0 m处，超声风速仪(CAST3，Campbell)数据采集器为CR3000 Campbell，采集数据包括风速、风向、温度、湿度以及仪器输出的摩擦速度，采样频率为10 Hz，观测时间为2013年7月1日至2014年6月30日；降水数据来源于鄱阳县气象基准站。

1.1 数据处理

对原始数据剔除降水日数据、去野点、去趋势、坐标旋转，重新计算30 min时间长度数据。

整体湍流特征(Internal Turulence Characteristics，简称ITC)是检验湍流发展的充分性的重要参数，通常认为ITC<30%时，湍流充分发展[11]。ITC的计算式为：

(1)

式(1)中，下标“ec”和“mod”分别为观测值和莫宁—奥布霍夫相似理论得到的计算值；σw为垂直风速标准差；u*为摩擦速度。Thomas和Foken[12]给出：

(2)

根据Gokede等[13]给出的湍流数据质量分级指标(表1)和Irwin[14]给出的L稳定度分类标准(表2)，QC为1—3表示质量好的数据；4—6代表质量较好的数据；7—8代表质量差的数据；9表示需要剔除的数据；A、B、C、D、E、F这6类分别对应了极不稳定、不稳定、弱不稳定、中性、弱稳定、稳定。文中对湍流观测资料进行检验(图1)，其中79.3%为质量好的数据(QC为1—3)，97.03%为质量较好数据(QC为1—6)，0.63%为需要剔除的数据。根据Gokede等[13]和Irwin[14]的分类并结合当地的实际情况，文中筛选出质量等级为1—3且为中性层结(L<-180.91或L>84.25)的数据。

表1 Gokede等(2004)给出的湍流数据质量分级指标[13]Table 1 Turbulence data quality classification index given by Gokede et al.(2004)

表2 Irwin(1979)给出的的L稳定度分类标准[14]Table 2 Classification criteria of Lstability given by Irwin (1979)

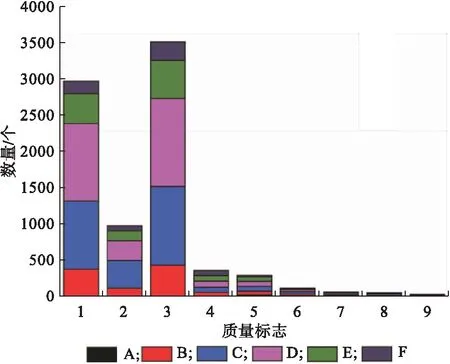
图1 湍流发展的充分性与稳定度分类统计Fig.1 Classification statistics of the sufficiency and stability for the turbulence development

Taylor[15]提出在满足某些条件的情况下，当湍流流经传感器时，可以认为湍流是被冻结的。其含义是在空间上一固定点对湍流的观测结果统计上等同于同时段沿平均风方向空间各点的观测，也称为定型湍流假设，当然湍流并不是真的被冻结，只是假设湍涡发展的时间尺度大于它被平流携带经过探头所需的时间，泰勒假设才适用。此假设中实际隐含着平稳气流和均匀湍流的条件，风速也不宜过小。为此，Willis 和 Deardorrff[16]提出以风速标准差(即湍流强度)作为使用假说的依据。湍流强度是表征湍流发展强度的量，即风速的标准偏差与平均风速之比。计算式为：

(3)

式(3)中，I为湍流强度；σ为风速标准差；u为平均风速。

图2给出了u、v、w方向的湍流强度与风速的关系。总体而言，Iu>Iv>Iw，垂直方向上湍流较弱。当风速>2 m·s-1时，湍流强度基本在0.4以下，且随着风速的增加，湍流强度减小，满足泰勒假设。当风速<2 m·s-1时，湍流强度变化值在0—1，呈显著的离散分布。随着风速的增大，湍流强度迅速减小，约在风速>2 m·s-1时趋于稳定。由此可知，风速较大时，观测的相对误差较小，湍流数据的稳定性也较强。因此，将风速<2 m·s-1的数据剔除。

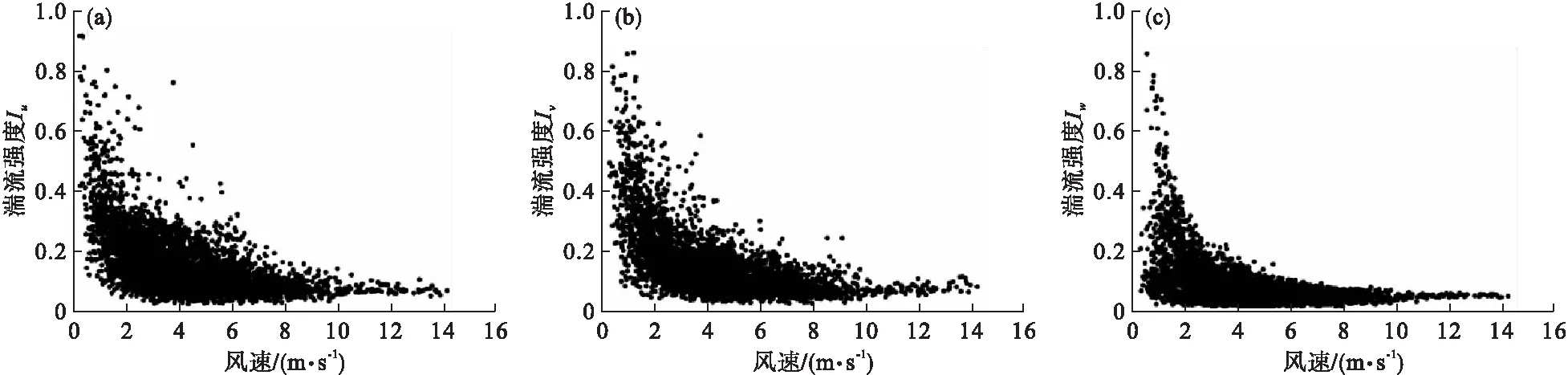
图2 u(a)、v(b)、w(c)方向的湍流强度与风速的关系Fig.2 Relationships between turbulence intensity and wind speed in u (a)、v (b) and w (c) directions

风速、温度和湿度的归一化标准差也称为湍流统计特征[17]，表征了对所有频率湍流信号进行统计分析的结果。

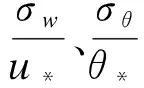
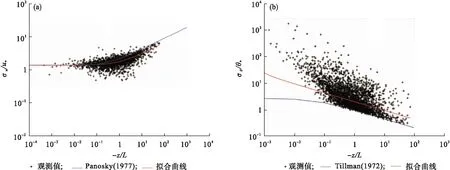
图3 归一化的垂直速度标准差(a)和温度标准差(b)Fig.3 Standard deviations of normalized vertical velocity (a) and temperature (b)

1.2 研究方法

零平面位移作为描述下垫面空气动力学特征的重要参数，常常用于边界层的湍流研究中，也是边界层参数化的重要参数之一。确定零平面位移的传统方法是利用中性近地面层风廓线进行计算，如果获得了3个或3个以上高度的风速梯度观测就可以用曲线回归求解。但是实际上该方法操作起来很难，因为首先中性层结资料的获取是十分困难的；其次也比较难于得到多个观测高度准确风速值的廓线。超声风温仪由于其测量精度高、性能稳定可靠、设计灵活等特点，是测量大气湍流数据的有效手段之一。

1.2.1 Martano方法

根据Monin-Obukhov相似性理论，风速廓线可写为：

u=(u*/k){ln[(z-d)/z0]-ψm(ζ)}

(4)

式(4)中，u*为摩擦速度；d为零平面位移；z0为动力粗糙度；k为Karman常数；ζ为稳定度；ψm(ζ)为集成了稳定度修正的函数。

文中采用Businger-Dyer-Webb[18]给出的经验公式。

(1)不稳定层结下，ζ=z/L<0

(5)

其中，x=(1-16ζ)1/4。

(2)稳定层结下，ζ=z/L>0

ψm(ζ)=-5ζ

(6)

同一高度上有多组平均量时，可用最小二乘拟合计算d和z0，计算式为：

〈{ku/u*-ln[(z-d)/z0]+ψm(ζ)}2〉=min (z0，d)

(7)

这是一个二元的非线性最小二乘问题，式(7)可以写为:

〈[S(z0，d)-p(z0，d)]2〉=min(z0，d)

(8)

其中，p(z0，d)=ln(z-d)/z0为参数。

当满足条件

〈S(z0，d)〉-p(z0，d)=0

(9)

或

(10)

式(8)可写为:

〈[S(z0，d)-p(z0，d)-〈S(z0，d)-p(z0，d)〉]2〉=min (z0，d)

(11)

由于p为参数，〈p〉=p，式(11)可写为:

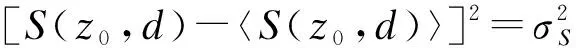
(12)

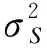
z0e=(z-d)exp〈-S〉≅(z-d)〈exp(-S)〉=〈z0〉m

(13)

1.2.2 TVM方法

Rotach[19]提出的通过测量温度脉动方差从而确定零平面位移和地表粗糙度的温度方差法，称为TVM法(Temperature Variance Method)。根据相似理论，在不稳定层结下，有下式：

(14)

在求得零平面位移和动力粗糙度后，可结合观测得到的u、L，利用式(4)计算摩擦速度u*与观测u*进行比较，其中相似性函数采用Businger-Dyer-Webb[18]给出的经验公式。

2 结果分析

2.1 季节变化

鄱阳湖地区四季分明，水域面积随季节变化明显，夏季最大、冬季最小，周边植被在春、夏季生长旺盛，秋、冬季节凋零。因此，文中将时间划分为春夏(3—8月)和秋冬(9月至翌年2月)两段，对零平面位移d进行拟合。

图4a和图4b给出了Martano方法计算的春夏和秋冬S的标准差σS随零平面位移d的变化，最小的σS对应的d为最佳值。分析可知，春夏季零平面位移d为2.6 m，对应的粗糙度z0为0.0145 m；秋冬季零平面位移d为4.3 m，对应的粗糙度z0为0.0023 m。可以看出，春夏季零平面位移要小于秋冬季，但粗糙度远大于秋冬季，为秋冬季的6倍多。这是因为春夏季鄱阳湖地区植被生长旺盛，但植被高度要小于秋冬季。可见地表粗糙度与下垫面的物理性质密切相关。

图4c和图4d给出了TVM方法计算的春夏和秋冬S的标准差σS随零平面位移d的变化。分析可知，春夏季和秋冬季的零平面位移d分别为8.0 m和7.5 m，对应的粗糙度z0分别为0.0370 m和0.0166 m，零平面位移d随季节的变化不大，但春夏季的粗糙度为秋冬季的2倍多。

图4 Martano方法计算的春夏(a)、秋冬(b)和TVM方法计算的春夏(c)、秋冬(d)S的标准差σS随零平面位移d变化Fig.4 The variations of the standard deviation σS of S in spring and summer (a),autumn and winter (b) calculated with Martano method and the corresponding values in spring and summer (c),autumn and winter (d) by TVM method with zero plane displacement d

2.2 湖面和陆面的变化

由于下垫面的不均匀，在观测塔的西边为湖面，其他方向为低矮灌木丛。文中定义270°—360°方向为来自湖面的通量，其他方向为来自陆面通量。图5a和图5b给出了Martano方法计算的来自湖面和陆面S的标准差σS随零平面位移d的变化。分析可知，湖面方向的零平面位移d为4.2 m，对应的粗糙度z0为0.0012 m；陆面方向的零平面位移d为8.6 m，对应的粗糙度z0为0.0122 m。可以看出，陆面方向的粗糙度是湖面的10倍。

图5 Martano方法计算的来自湖面(a)、陆面(b)和TVM方法计算的来自湖面(c)、陆面(d)S的标准差σS随零平面位移d的变化Fig.5 The variations of the standard deviation σS of S in spring and summer (a),autumn and winter (b) calculated with TVM method and the corresponding values in lake surface (c),land surface (d) by TVM method with zero plane displacement d

图5c和图5d给出了TVM方法计算的来自湖面和陆面S的标准差σS随零平面位移d的变化。分析可知，湖面方向的零平面位移d为3.2 m，对应的粗糙度z0为0.0034 m；陆面方向的零平面位移d为4.4 m，对应的粗糙度z0为0.0132 m。

2.3 两种方法计算结果对比分析

表3给出了Martano和TVM方法计算的零平面位移d和粗糙度z0。分析可知，用Martano方法计算的结果随季节变化较大，春夏季的粗糙度z0是秋冬季的6.3倍。而用TVM方法计算的零平面位移d春夏和秋冬季相差不大，粗糙度z0春夏季是秋冬季的2.2倍。用Martano方法计算的陆面方向零平面位移d和粗糙度z0分别为来自湖面的2倍和10倍，而用TVM方法计算的结果分别为1.4倍和3.9倍。可以看出，Martano方法对季节和方向更敏感。

表3 Martano和TVM方法计算的零平面位移d和粗糙度z0Table 3 Zero plane displacement d and roughness z0 calculated with Martano and TVM methods m

分别用不同方法计算得到年平均d和z0，代入Monin-Obukhov相似性理论的风廓线关系式(4)计算摩擦速度。图6给出了计算的摩擦速度和实测摩擦速度的线性回归。分析可知，利用Martano方法计算的摩擦速度与实测值的拟合曲线为y=1.099x，对摩擦速度造成了约9.9%的高估。TVM方法计算的摩擦速度与实测值的拟合曲线为y=1.328x，对摩擦速度造成了约32.8%的高估。由此可见，用Martano方法计算零平面位移d和粗糙度z0代入Monin-Obukhov相似性关系中计算的摩擦速度和观测值有较好的一致性。

图6 Martano(a)和TVM(b)方法计算的摩擦速度和实测值的线性回归Fig.6 The linear regressions between the measured friction velocity and that calculated with Martano (a)and TVM (b) methods

文中计算的陆面和湖面的d和z0与前人研究相比存在一定的差异。Sorbjan[20]给出的平坦下垫面z0量级在10-3m左右，Stull[21]给出的广阔水域z0量级在10-3—10-4m，Verburg和Antenucci[22]计算Tanganyika湖(世界第三大湖)的z0量级在10-5m左右。其原因可能与湖体面积及深度有关，也与大气稳定度有关。

3 结论

(1)Martano方法的计算结果随季节变化较大，春夏季的粗糙度z0是秋冬季的6.3倍。TVM方法的计算结果季节变化不大，粗糙度z0春夏季是秋冬季的2.2倍。

(2)Martano方法计算的陆面方向零平面位移d和粗糙度z0分别为来自湖面的2倍和10倍，而TVM方法计算的结果分别为1.4倍和3.9倍。

(3) Martano方法计算的摩擦速度与实测值的拟合曲线为y=1.099x，对摩擦速度造成了约9.9%的高估。TVM方法计算的摩擦速度与实测值的拟合曲线为y=1.328x，对摩擦速度造成了约32.8%的高估。用Martano方法计算的摩擦速度和观测值有较好的一致性。