宇航产品振动试验用夹具绝对传递率的问题分析研究*

杨静静，孙杰明，马小明

(1.中航富士达科技股份有限公司泰斯特实验室，西安 710077；2.西安东仪综合技术实验室有限责任公司，西安 710065)

0 引言

在振动试验中，夹具作为一个机械结构件，希望通过夹具可以将振动台的激励能量1∶1的传递给被试产品，因此考虑的并不是夹具本身如何振动[1]，而是振动台传递给夹具的激励能量是多少，夹具传递的给被试产品的激励能量是多少，以及在这种传递的过程中又会损失多少的激励能量，为此，必须分析夹具的绝对传递率。

1 单自由度有阻尼强迫振动的原理

由于在进行振动试验时，产品附带的夹具必不可少，而如果将夹具整体看作是一个惯性负载，而夹具与振动台相连的螺钉或者压板可以看成一个具有一定弹性模量的弹簧，所以被试产品和夹具可以整体看成一个等效的弹簧-质量系统，夹具在受到振动台的激励后，其运动状态符合单自由度有阻尼强迫振动的规律，很显然夹具在收到振动台的激励后，自身的响应会消耗一部分激励能量，而后将剩下的激励能传递给被试产品[2-3]，其原理如图1所示：

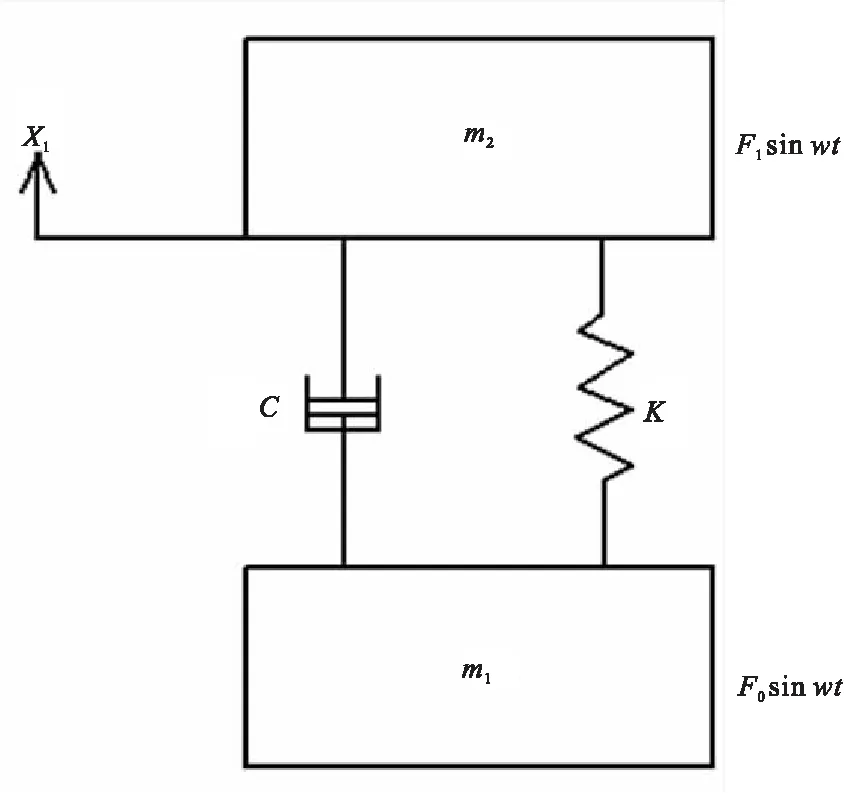
图1 夹具与被试件连接简化图

取X方向为正方向m1为一个受到振动激振力(F0sinwt)激励的惯性负载，其中K为振动台和夹具相连螺钉其弹性系数为K，而C为系统阻尼，m2为受到传递激振力(F1sinwt)激励的被试件，根据单自由度有阻尼强迫振动的规律，可以得夹具的力学二阶线性常系数非其次微分方程为：

(1)

设式(1)通解为x=x0sin(wt-φ)带入式(1)中得：

F0sinwt=-mw2x0sin(wt-φ)

+cwx0cos(wt-φ)+kx0sin(wt-φ)

(2)

将式(2)移项得：

F0sinwt=(k-mw2)x0sin(wt-φ)

+cwx0cos(wt-φ)

(3)

将F0sinwt改写为F0sin[(wt-φ)+φ]带入式(3)中得：

F0sin[(wt-φ)+φ]=

(k-mw2)x0sin(wt-φ)+cwx0cos(wt-φ)

⟹F0sin(wt-φ)cosφ+F0cos(wt-φ)sinφ

=(k-mw2)x0sin(wt-φ)+cwx0cos(wt-φ)

⟹(k-mw2)x0sin(wt-φ)-F0sin(wt-φ)cosφ

+cwx0cos(wt-φ)-F0cos(wt-φ)sinφ=0

⟹[(k-mw2)x0-F0cosφ]sin(wt-φ)

+(cwx0-F0sinφ)cos(wt-φ)=0 (4)

从式(4)可知在t为任意值时都应满足式(4)，因此有：

(k-mw2)x0=F0cosφ

cwx0=F0sinφ

(5)

由式(5)可以得出：

(6)

(7)

2 绝对传递率

从式(7)及图1可知此时被试件m2所受到的激振力仅仅是弹力和阻尼力的合力F1即：

(8)

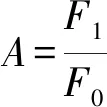
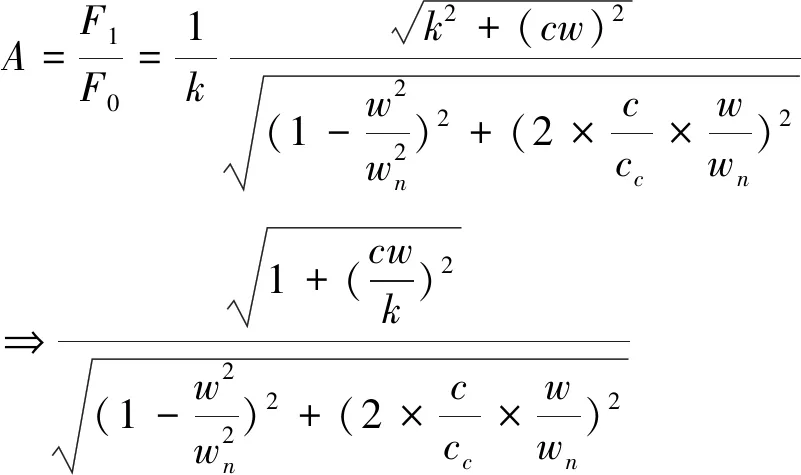
(9)

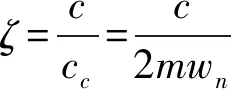
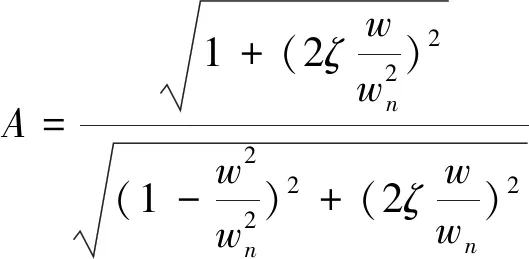
(10)

其中wn为系统有阻尼自由振动的临界频率，ζ为无因次相对阻尼系数，则从式(10)中可以看出夹具的绝对传递随着系统振动频率的变化分为以下几种状态：

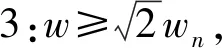
状态4：w=wn，此时传递率与无因次阻尼系数ζ成反比。

由此可知，在振动试验解决的传递率是与夹具自身的动态特性有关，且当振动频率与夹具自身的谐振频率比值小于1.414时，振动的输入激振能量，只要很少的一部分消耗在被试件的夹具上，而更多的激振能量传递到了被试件上[4-6]。在当振动频率与夹具自身的谐振频率比值大于1.414时，传递效率会非常的差，大部分的激励能量都损耗在夹具自身的响应，而传递到被试件的激励能量则非常的少，从式(10)可以看出，w/wn的比值越大，消耗于夹具振动的能量就越多，通过夹具传递给试验件的能量就越少。因此，在设计夹具时，作为多自由度弹簧质量系统，夹具的整体谐振频率应高于最高振动频率的0.7倍。

3 半功率带宽法测定相对阻尼因数

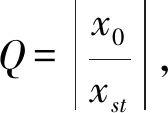
(11)

而其最大静位移可以表示为：

xst=F0/K

从式(11)可知在系统发生谐振时，w=wn，此时的谐振峰值为：

(12)

则Q、Qmax分别为：

(13)

(14)

根据式(13)和式(14)的结论可得：

(15)

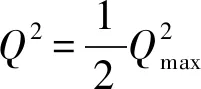
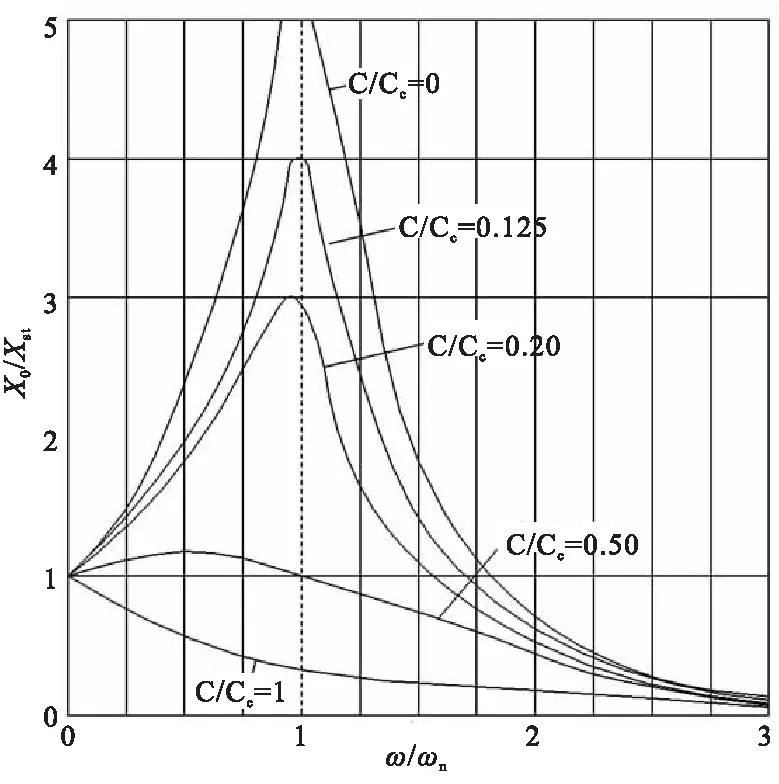
图2 单自由度有阻尼振动强迫振动幅频特性

如图2所示在有阻尼的情况下，振动系统在发生谐振时的振动频率其实并不发生在w/wn=1时，因此，对式(15)中w进行微分可得：

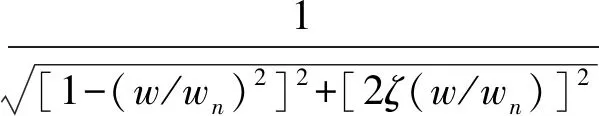
(16)

则：-4(1-λ2)λ+8ζ2λ=0

⟹-4(1-λ2)λ+8ζ2λ=0

⟹-(1-λ2)λ+2ζ2λ=0

⟹-(1-λ2)+2ζ2=0

(17)

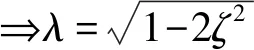
(18)

(19)

对式(19)取倒数，同时去根号进行化简得：

(20)

(21)

在实际的振动试验中相对阻尼因数较小因此ζ2可以忽略，则：

(22)

因此w对应的两个频率点为：

(23)

将上式相减得：

(24)

则式(23)计算的结果可以表示为：

(25)

其中fa，fb为半功率带频率点如图3所示。

在振动试验中如果能测得如图所示的响应曲线，就能够利用式(25)的相对阻尼系数，在使用式(25)计算相对阻尼系数时，虽然有误差，但是非常的实用。

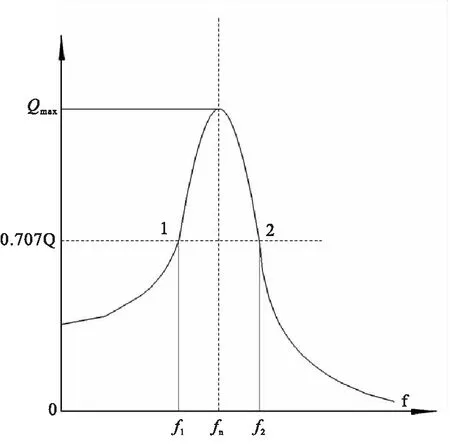
图3 半功率示意图

4 结论

在实际的振动试验中，由于振动台的限制，试验参数的限制，在进行试验时，希望尽可能的将振动台的激励能量1∶1的传递给被试产品[11]，但是因为夹具的存在(夹具又限制于材料及现有加工工艺的影响)，这个理想的结果往往很难实现，在产品振动的同时，夹具的自身的响应，不可避免的会消耗激励能量，在这个过程中，通过对夹具的设计和分析，尽可能的让总的激振能量尽可能多的传递给被试产品，通过公式推导出无因此阻尼系数、绝对传递率计算公式，可以让这种传递关系、数字化、量化的表示出来，虽然有误差，但是在工程测量中这个误差是可以被允许的[12]。通过公式的计算，可以让实验操作人员明确被试件与夹具之间的能量转化关系，同时可以让产品设计人员和夹具设计人员更好的明确产品在试验过程中的薄弱点，以及产品的危险频率。对后续的振动试验，提供数据以及技术指导，这在实际工程计算中有着重要的意义。