钢结构建筑物稳定性分析
王成 中铁十七局集团有限公司勘察设计院
1 前言
一般而言,依据钢结构建筑物的失稳性质对失稳现象进行划分的话,主要可以分为枝点、极限点和跳跃失稳3大类别,其中,枝点失稳又可以被叫作平衡分岔失稳。具体见图1。
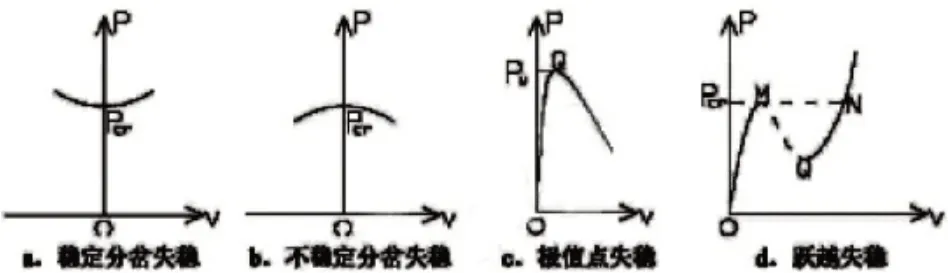
图1
2 线性特征值屈曲分析
特征值屈曲分析实际就是结构的弹性稳定性分析,详细论述为:原来平衡基础上,结构受到载荷作用从而产生的第二种平衡状态。通过软件的特征值屈曲分析,计算得到屈曲模态及各个模态对应的屈曲荷载系数,荷载系数是非常重要的,因为屈曲荷载系数乘以外加荷载为屈曲荷载。
特征值计算公式:
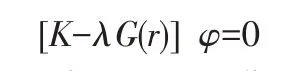
K——结构的刚度矩阵;λ——屈曲因子;G(r)——某种荷载所引起的几何刚度;φ——屈曲模态所组成的阵型矩阵。
3 非线性屈曲分析
非线性屈曲分析需要充分的对材料的非线性、结构最初状态下的几何缺陷等进行全面考虑,在此基础上,进行模拟分析结构的几何大变形非线性状态。最为常用的是“一致缺陷模态法”来开展结构非线性屈曲分析中初始几何缺陷的引进应用,换而言知为:通过应用结构最易发生的屈曲模态实现对结构初始缺陷分布情况的模拟。
4 工程概况
山西某集团拟新建一座大跨度封闭防尘罩。防尘罩屋面采用单层彩色压型钢板,防尘罩内设置自然采光带。防尘罩效果图详见图2。

图2 防尘罩效果图
防尘罩横向跨度约为80m,纵向长度约为168m,防尘罩高度为27m,矢跨比f/l=0.3375,两端采用固定铰支座,每隔两端施加平面外约束模拟次桁架。12m是榀拱桁架的标准布置间距,图3为立体结构布置示意图。

图3 结构布置图
5 模型设计参数
结构拟建在曲沃地区,根据《抗规》2010版,该区域地震设计为第一组,基本地震加速度数值设计为0.20g,抗震设防烈度为8度。场地类别为三类,地震影响系数在多遇地震下最大值为αmax=0.16,Tg=0.45s为其的特征周期值,钢结构阻尼比取ξ=0.02,设置50年为结构设计基准期。
Q235B级钢材是拱桁架模型所应用的材料,采用3d3s进行截面设计,经设计截面型号为:
上弦杆:φ219×10;下弦杆:φ219×12,φ219×10;
腹杆:φ180×6,φ140×8,φ140×6,φ114×8,φ114×4,φ89×4,φ83×6,φ76×4。
计算模型如图4所示。

图4 标准几何模型
6 拱桁架的稳定分析
稳定分析中,模拟均布荷载,将荷载等效为节点荷载施加在结构的上弦节点上,如图5所示。

图5 恒载显示
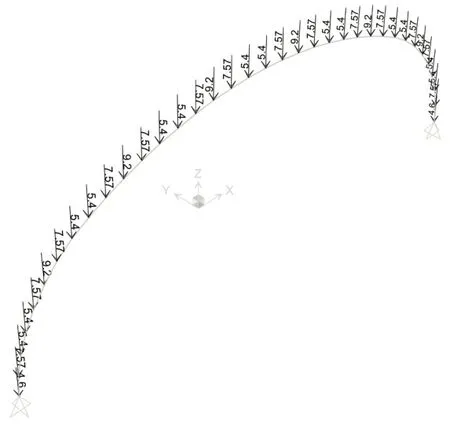
图6 活载显示

图7 左半跨活荷载显示

图8 右半跨活荷载显示
6.1 特征值屈曲分析
针对球面网壳的全面分析中,可以依据JGJ 7—2010《空间网格结构技术规程》第4.3.3条规定采用满跨均布荷载开展分析,在充分考虑椭圆抛物面和圆柱面网壳的满跨均布荷载基础上,还需要对分布的半跨活荷载情况进行全面考虑,同时,还需要对半跨活荷载影响进行充分考虑后,进行网壳全过程分析。通过采取结构最低阶屈曲模态进行初始几何缺陷分布情况的分析,可以依照网壳跨度的1/300进行缺陷最大计算值的取值。
①将满跨竖向荷载作用在上弦节点,其前6阶屈曲因子见表1。
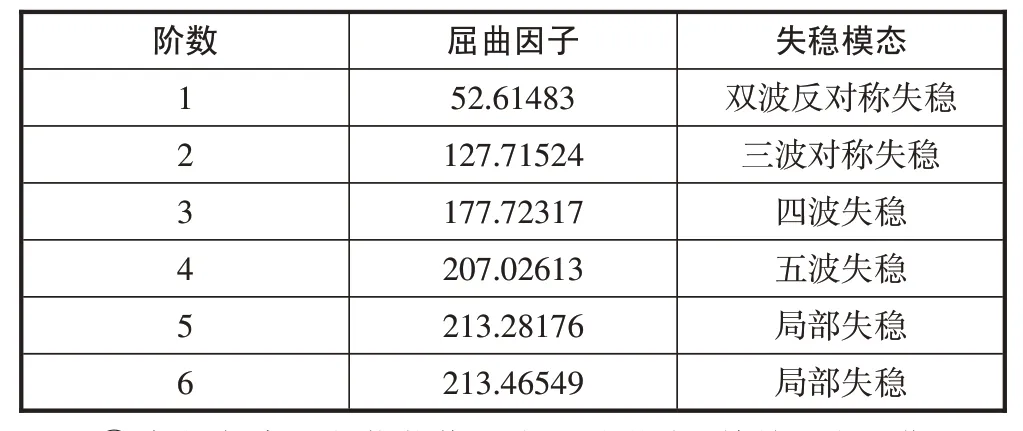
表1 满跨竖向荷载作用下特征值屈曲因子
②将右半跨竖向荷载作用在上弦节点,其前6阶屈曲因子见表2。

表2 半跨竖向荷载作用下特征值屈曲因子
该模型加载满跨竖向荷载作用时前四阶失稳模态为整体失稳,第五阶屈曲荷载远远大于第一阶屈曲荷载,数值大约是其的4.05倍,由此可以认定,该结构的局部稳定性较大。
前三阶失稳模态在加载半跨竖向荷载作用下呈现出整体失稳状态;后三阶均为局部失稳,与第一阶屈曲荷载相比较的话,第四阶屈曲荷载是其的3.45倍,由此可以认定,在加载半跨竖向荷载时,该结构局部稳定性较小。
6.2 几何非线性稳定性分析
结构相应的临界荷载在竖向全跨及半跨荷载作用下,初始阶段节点荷载较小时,位移与荷载呈线性关系,由此可以认定,结构此时刚度较大;荷载进一步持续增加,位移迅速增大;最终,结构达到临界荷载时,结构发生整体失稳破坏。
7 结束语
(1)大跨度拱桁架应考虑几何非线性对拱桁架的稳定性影响,以保证结构安全性。
(2)钢管拱桁架受到(满跨和半跨)的不同荷载作用方式下,其的临界荷载呈现出显著差异性,其中,临界荷载以半跨竖向荷载作用下最小。因此,需要全面考虑多种荷载的作用方式对大跨度钢管拱桁架的稳定性开展分析。

