立足于数学本原 提高数学抽象素养——一道解析几何题的探讨与推广

江苏省泰州市罗塘高级中学 赵允星

文章通过对一道高三模拟题的思考，层层递进地设计出一系列具有高度思维价值的问题，定位于高考考查的重难点，立足于数学的本原，更有利于培养学生分析问题和解决问题的能力。

《普通高中数学课程标准》提出了高中数学六大核心素养，即：数学建模、数学运算、直观想象、数据分析、逻辑推理、数学抽象。从数学发展的角度来看，要求学生会用数学的眼光观察问题、会用数学的思维思考问题、会用数学的语言表述问题。因此，培养学生的数学抽象思维是数学教学的核心。而如何培养学生的数学抽象素养是当今绝大多数老师思考的问题。常见的数学教学有三种模式：一是以情境创设为开篇，逐步引导学生认识新知识，再以例题讲解加以巩固；二是以知识点为主线，以点带题，层层深入；三是以例题为载体，将知识点串联起来。然而在日常的教学过程中，很多老师都会遇到这样的问题：学生在遇到一些有难度的题目时往往观察不出问题的结构，以致无法关联相关的知识。笔者在一道高三模拟题研究的基础上进行推广探究，这样可以实现知识的类比联系，以提高学生的数学抽象素养。

一、问题呈现

例题：如图所示，F为抛物线C：y2=8x的焦点。过点F的直线l与抛物线C交于M、N两点。试确定在x轴上是否存在点P，使得PM、PN关于x轴对称？若存在，请求出P点的坐标；若不存在，请说明理由。

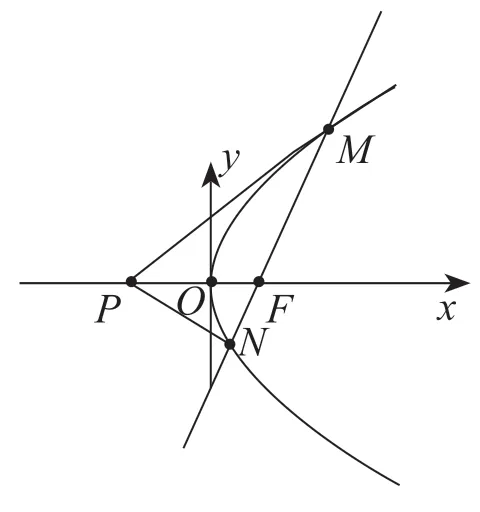
解法探究一：若存在点P，使PM、PN关于x轴对称，则kPM=-kPN，由此求得P点坐标。

由kPM+kPN=0 得a=-2，此时P（-2，0）。

所以，当直线l垂直于x轴时，此时P为除F的一切点；当直线l不垂直于x轴时，P点坐标为（-2，0）。

解法探究二：若存在点P，使得PM、PN关于x轴对称，由对称性可知，点N关于x轴的对称点N1为PM与抛物线的交点，可以证明直线MN1过定点P。

解答：（1）若直线l垂直于x轴，此时P为除F的一切点。

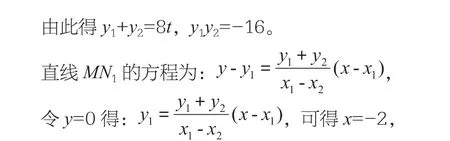
即点P坐标为（-2，0）。

所以，当直线l垂直于x轴时，点P为除F的一切点；当直线l不垂直于x轴时，P点坐标为（-2，0）。

针对本题，若只是通过常态的教师展示讲授，可能导致学生对于题目的理解和把握仅仅停留在机械的记忆和模仿层面，缺乏思考与探究，更不能灵活地整合知识、迁移知识，无法解决类似的问题。这显然与新课程理念不相符。笔者希望学生能将这道例题的研究方法和思维形式化为思维习惯，从而使学生能够触类旁通，进而提升学生的数学综合素养。在有了类似的解题经验之后，根据数学抽象可以将已有数学命题进行整合类比，进而推广到更一般的情形中，能够在新的情境中选择和运用数学方法来解题，以达到触类旁通的效果，这正是数学抽象素养的内涵要求。

二、推广探究

PM，PN关于x轴对称？

解法探究：若存在点P，使得直线PM，PN关于x轴对称，由对称性可知，点N关于x轴的对称点N1为直线PM与椭圆的交点，可以证明直线MN1过定点P。

解答：设M（x1，y1），N（x2，y2），则N关于x轴的对称点为N1（x2，-y2）。

三、反思与结语

本文立足于数学的本原，采用特殊到一般的数学思想，通过“例题+推广探究”的形式，让学生体会从一个问题到一类问题的归纳过程，从而抓住圆锥曲线中定值定点问题的本质，同时学会用数学的眼光处理结构→提取特征→关联知识思想方法→生成解法→解决问题，这是数学抽象素养的内涵，也是落实数学抽象核心素养的要求。