基于特征值分解的多阵元空频抗干扰技术研究

丁 可，康 博，张新帅，李 军，沈 磊，肖永丽

(1.四川九洲电器集团有限责任公司，四川 绵阳 621000；2.四川九洲北斗导航与位置服务有限公司，四川 绵阳 621000)

0 引 言

随着北三组网，我国北斗卫星导航系统已在各行各业得到广泛的应用，成为不可或缺的一部分。但由于卫星轨道距离地面十分遥远，接收到经过空间衰减后的北斗卫星信号功率很低，远小于环境噪声，因此容易被无意或有意的干扰信号所影响，造成定位精度下降甚至完全失效，因此需要增加抗干扰处理，对干扰信号进行滤除。目前主要的抗干扰方法主要有时域抗干扰技术、频域抗干扰技术、空域抗干扰技术、空时抗干扰技术和空频抗干扰技术等[1-2]。其中时域抗干扰技术和频域抗干扰技术只能针对带宽较窄的干扰信号抑制，对宽带干扰信号无效；空域抗干扰技术对窄带和宽带干扰信号均能进行抑制，但由于其同等阵元数情况下自由度低，抗干扰性能较差；空时抗干扰技术和空频抗干扰技术通过多域联合，提升了自由度，具备良好的抗干扰性能。空频抗干扰技术与空时抗干扰技术相比，运算复杂度相对较低，且随着频域观测维度的增加，能够减小信号失真导致的伪距和载波相位误差[3-4]。

随着电磁环境越来越复杂，要求可抗干扰的数量也随之增大，导致天线阵元增多，自相关矩阵求逆计算量急剧增大，因此需要在不影响抗干扰性能的情况下对自相关矩阵求逆进行变换处理，降低复杂度，便于实际工程上的应用。用基于特征值分解的空频抗干扰技术对自相关矩阵进行特征值分解，利用其Hermitian矩阵的特性，通过特征值和特征向量得到自相关矩阵的逆矩阵，从而避免了高阶矩阵直接求逆，降低了计算难度，便于工程实现。本文对其进行了仿真分析及实物测试验证，证明了基于特征值分解的空频抗干扰技术的有效性。

1 空频抗干扰技术

空频抗干扰技术通过快速傅里叶变换(FFT)将阵列天线接收到的每路信号在频域上等分为N个子带，之后通过空域抗干扰技术对每个子带内的干扰信号进行滤除[5]，结构如图1所示。

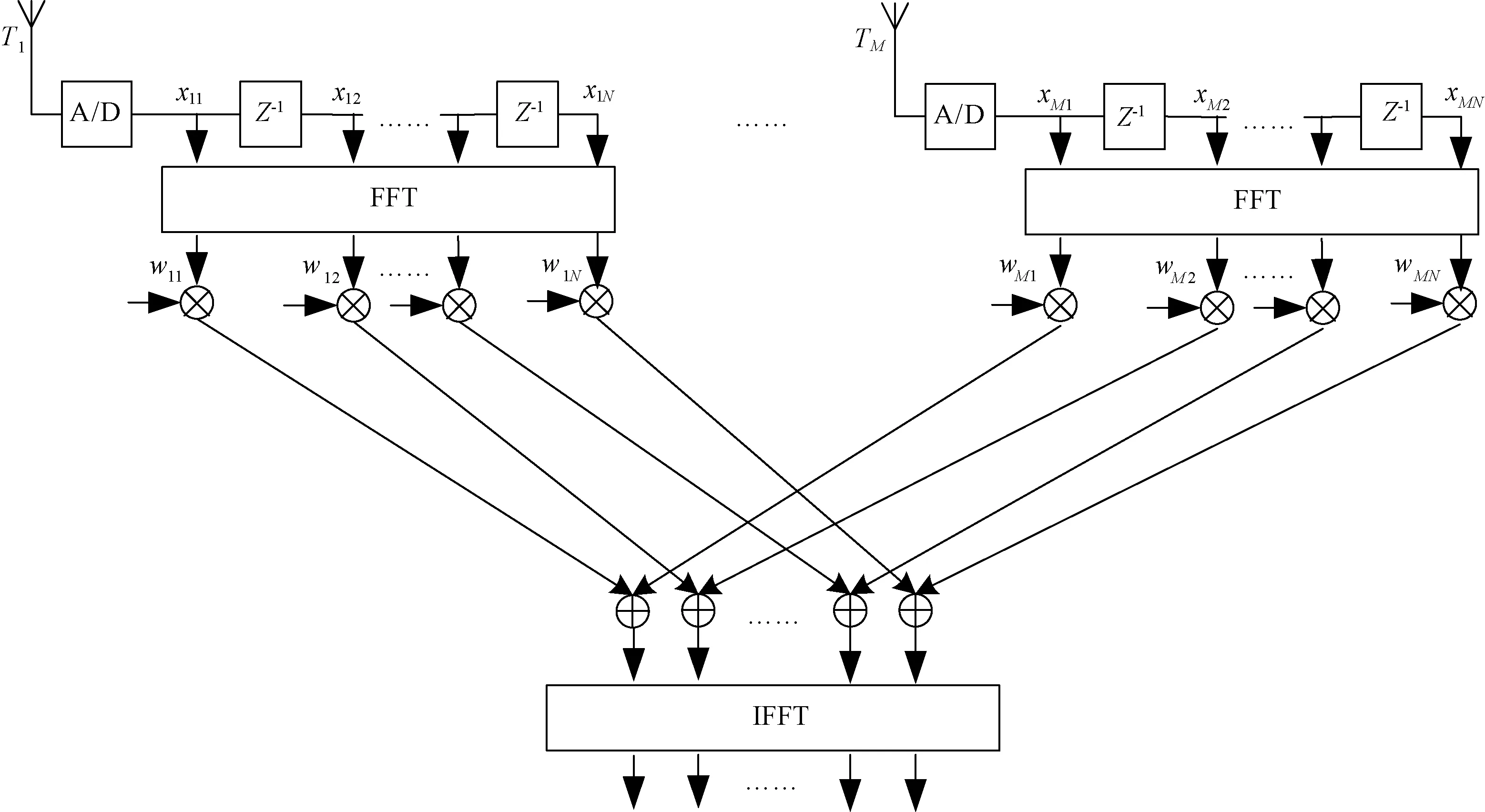
图1 空频抗干扰处理结构

设M为天线阵元个数，N为需FFT的点数(即模/数转换(ADC)连续采样的N个数据)，每N个数据经过FFT之后划分的N个子带可以表示为：

F={F1,F2,…,FN}

(1)

第n个子带数据Fn表示为：

Fn=[f1n,f2n,…,fMn]T

(2)

权值矢量W表示为：

W={W1,W2,…,WN}

(3)

第n个子带权值Wn表示为：

Wn=[w1n,w2n,…,wMn]T

(4)

每个子带均可采用最小方差无失真响应准则：

(5)

式中:RFnFn表示每个子带的自相关矩阵；Sn表示导向矢量。

每个子带的最优权值Wnopt可以表示为：

(6)

实际应用中，阵元数M随着要求在逐渐增大，导致自相关矩阵直接求逆变得难以实现。

2 基于特征值分解的空频抗干扰技术

每个子带的自相关矩阵RFnFn采用JACOBI法(JACOBI法此处不再详细叙述，其中涉及的三角函数运算可通过CORDIC旋转法进行求解)进行特征值分解：

(7)

式中:qin表示第n个子带自相关矩阵的第i个特征向量;λin表示表示第n个子带自相关矩阵的第i个特征值。

利用Hermitian矩阵特性，RFnFn的逆矩阵可以表示为：

(8)

将上式代入式(6)可得：

(9)

采用功率倒置，导向矢量Sn=[1,0,…,0]T，上式可简化为：

(10)

式中：*表示共轭；qi1n表示第n个子带第i个特征向量的第一个元素。

3 仿真试验

3.1 基于特征值分解的空频抗干扰性能仿真

仿真条件：均匀圆阵，阵元数M=7，有用信号入射方向(俯仰角25°，方位角100°)，信噪比-25 dB；6个干扰信号入射方向分别为(-20°，30°)、(-5°，65°)、(10°，120°)、(50°，200°)、(62°，270°)、(80°，330°)，干信比均为80 dB；FFT采样点数为1 024；子带过多，不便于观察每个子带的零陷图，通过抗干扰前后频谱性能对比，仿真结果如图2、图3所示。

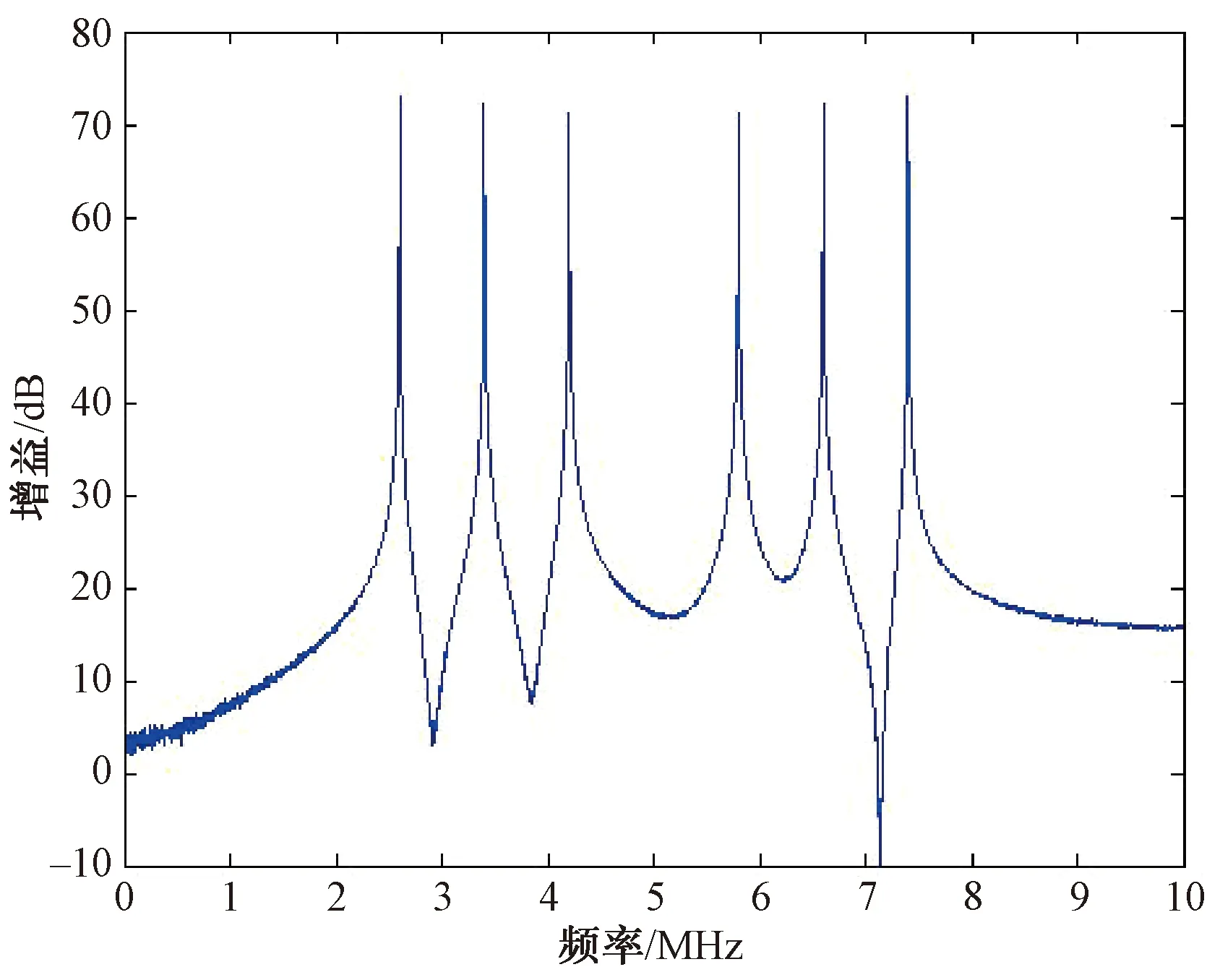
图2 接收到的信号频谱

图3 抗干扰后信号频谱

对比图2和图3可知，经过基于特征值分解的空频抗干扰运算后，对6个不同方向的干扰信号均能够有效滤除，抑制在环境噪声以下，便于后续卫星信号的捕获跟踪。

3.2 直接求逆与基于特征值分解的抗干扰性能对比

仿真条件：均匀圆阵，阵元数M=7，信噪比-25 dB；6个干扰信号的干信比均为80 dB，干扰类型依次设置为单频干扰、窄带干扰(1/10带宽)、宽带干扰和混合干扰(2个单频干扰、2个窄带干扰、2个宽带干扰)，每类干扰类型仿真100次，输出信干噪比的平均值结果如表1所示。

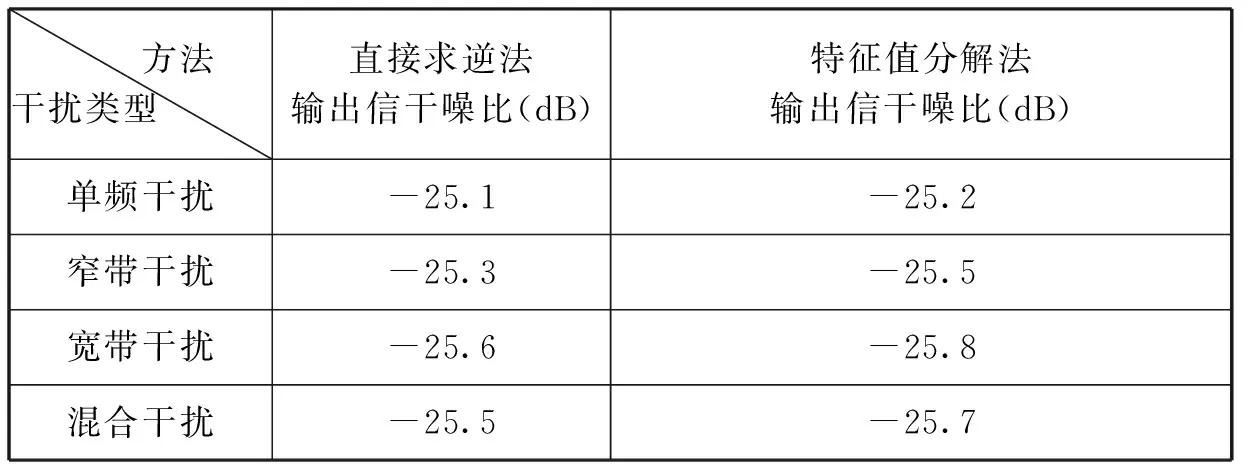
表1 输出信干噪比

从表1可以看出，在4个单频干扰、窄带干扰、宽带干扰或者混合干扰情况下，2种方法对空频抗干扰算法输出信干噪比的影响基本相同，都能够有效抑制干扰信号。

4 试验验证

室外测试场景如图4所示。

图4 室外测试场景

图4中，0号位置的转台上为七阵元抗干扰天线，1～6号为干扰信号发射天线，分别发射单频、窄带、宽带、脉冲以及扫频压制干扰信号，达到转台处7阵元抗干扰天线的干信比均为75 dB，转台水平方向0～360°、俯仰方向-10°～+10°循环转动。每种压制干扰类型测试5 min，取1σ，接收机定位精度见表2。

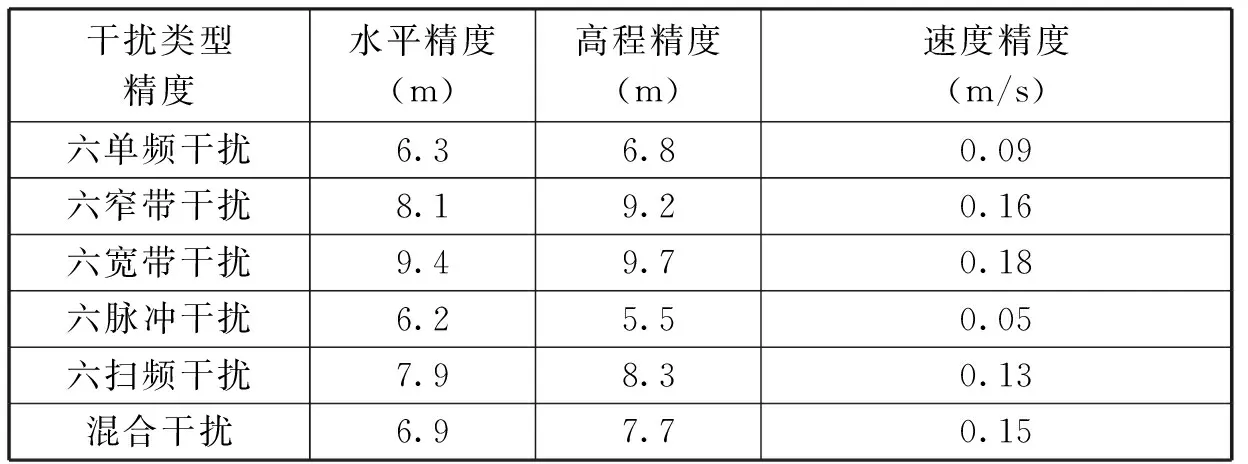
表2 经过基于特征值分解的空频抗干扰算法后的定位精度

从测试结果可以看出，后端接收机位置精度<10 m，速度精度<0.2 m/s，基于特征值分解的空频抗干扰技术能够有效抑制单频、窄带、宽带、脉冲、扫频、混合等各种类型的干扰信号。在各类型干扰中，基于特征值分解的空频抗干扰技术对宽带干扰的抑制能力最差，对单频干扰的抑制能力最好。

5 结束语

空频抗干扰技术通过空域与频率的联合，增大了自由度，具有良好的抗干扰性能，但随着阵元数的增多，自相关矩阵直接求逆变得越来越难以实现。本文对基于特征分解的空频抗干扰技术进行了研究，利用自相关矩阵的Hermitian特性，通过特征分解避免了高阶自相关矩阵的直接求逆，降低了计算难度，且抗干扰性能与自相关矩阵直接求逆性能基本相同，同时在FPGA平台上进行了工程实现，并对其抗干扰性能进行了室外真实环境测试。