基于稀疏重构的蜂窝夹层复合材料板中Lamb 波传播特性估计方法

高 飞，姬鼎丞，韩 潇，王军伟，綦 磊，林 京

（1. 北京航空航天大学 可靠性与系统工程学院，北京 100191； 2. 北京卫星环境工程研究所，北京 100094；3. 北京航空航天大学 宁波创新研究院，宁波 315832）

0 引言

蜂窝夹层复合材料由两块高强度复合材料面板和中间蜂窝芯层黏结固化而成，具有比强度高、抗疲劳能力强、隔振降噪性能好等优势，广泛应用于航天器结构本体和承力部件的制造。然而，由于制造工艺复杂、服役环境严苛以及工况条件多变等因素，蜂窝夹层复合材料表面及其内部易产生裂纹、分层、脱粘等不易辨识的损伤，给航天器装备的结构完整性和可靠性带来巨大隐患。

随着航天装备结构的日益大型化和复杂化，传统结构健康监测和无损伤检测方法在检测效率、对损伤敏感性和损伤评估等方面难以满足当前的结构检查要求。而超声Lamb 波是在薄壁结构中传播的一种弹性波，具有能耗低、传播距离远、对结构内部和表面损伤均敏感、一次传播可捕获传播路径中的结构信息等优势，可适应大型航天器装备结构的在线监测和离线诊断需求。超声导波检测在复合材料损伤的诊断、定位、成像和评估等方面取得了一系列进展，然而上述应用均需要先验的导波传播特性曲线作为算法基础。

对于复杂复合材料结构，受加工工艺、服役环境及物理模型等影响，其理论参数难以准确匹配实际结构，此时经典的Rayleigh-Lamb 方程求解频散曲线方法将不再适用。因此，理论求解和有限元仿真方法难以获取与实际相符的导波传播特性曲线。相比而言，实验方法可避免对结构实际物理参数的依赖，以测试数据为依托，通过提取信号特征实现各模态成分时延信息表征。例如，Draudviliene 等提出了相邻测试信号相位差表征方法，可以准确估计基础模态Lamb 波的相速度；郑祥明等采用时频分析方法，基于时频重排和特征提取实现了Lamb 波局部群速度估计；刘增华等通过对波场信号进行二维傅里叶变换，实现了Lamb 波的频率‒波数估计；许凯亮等采用多激励和多接收传感方式，通过稀疏SVD 方法实现了宽带频散曲线的准确估计。然而，上述实验求取Lamb 波传播速度的方法在模态溯源和数据量要求方面仍有不足。

针对上述问题，基于压缩感知稀疏重构方法的提出，可在少量测试信号下以Lamb 波的频率‒波数域稀疏表达为约束，对传播特性曲线进行准确重构，不仅能够实现所有可激发导波模态信号的重构，还可极大降低对信号的测试量要求，因此更加适用于实验求解Lamb 波的传播特性曲线。本文提出一种基于稀疏重构的Lamb 波传播特性估计方法，将有限的测试信号进行频率‒波数域表达，从而提取可激发Lamb 波的传播速度曲线。

1 结构中的超声导波与传播模型

1.1 薄壁结构中的超声导波

Lamb 波是薄壁结构中由上下表面反射的横波和纵波相互耦合而成，沿着板平面传播的一种弹性波。根据Lamb 波传播过程中结构质点的振动方向，Lamb 波可分为对称模态和反对称模态（见图1），且每种模态均包含多种子模式，称为Lamb波的多模态特性。此外，Lamb 波的传播速度与激发频率和板厚相关；与体波不同，Lamb 波的速度是非线性变化的，因此具有频散特性。以均质各向同性的铝板（杨氏模量71 GPa, 泊松比0.33，密度2700 kg/m）中的导波传播特性为例（见图2），金属板中Lamb 波的相速度理论曲线除基础Lamb 波模态（A0 和S0）外，在激发频率超过高阶截止频率时，将会产生更多的模态成分。

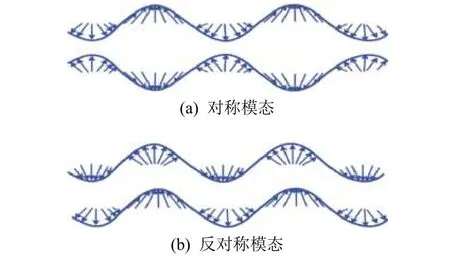
图1 Lamb 波的振动模式Fig. 1 Modes of vibration of Lamb wave

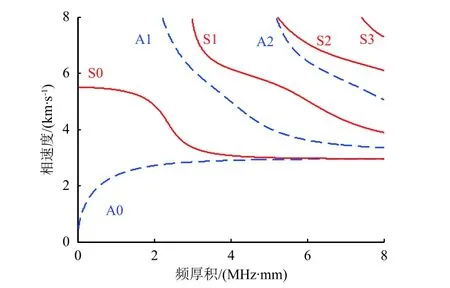
图2 铝板结构中的超声Lamb 波相速度Fig. 2 Phase velocity of ultrasonic Lamb wave in aluminum plate structure

多模态和频散特性是Lamb 波实现结构缺陷定位和评估的基础。当结构中存在缺陷时，结构连续性的改变将严重影响Lamb 波的传播特性，引起导波的散射和模态转换等现象。因此，基于Lamb波的传播特性，提取测试信号的异常特征，可表征损伤的位置、程度及类型等重要信息，为结构的完整性评估提供依据。然而，Lamb 波的频散和多模态同时给损伤特征的提取带来不利影响，例如：Lamb 波多模态成分彼此叠加会加剧接收信号的复杂程度，使得由损伤引起的散射成分极易被边界反射成分或其他模态成分所淹没；受频散特性的影响，导波能量在时间域发生扩散，随着导波传播距离的增大，波包持续时间明显增长且信号的信噪比下降，还会增加波包叠加概率。因此，获取Lamb 波的先验传播特性曲线不仅可为解析Lamb 波信号提供依据，也是决定损伤检测结果可靠性的重要前提。

1.2 超声导波的散射模型

Lamb 波在结构中传播的数学模型取决于传感器的位置和波传播特性曲线。在模型建立过程中，通常将超声Lamb 波的传播视为平面波，超声以激励源为圆心，向四周均匀辐射。对于目标的Lamb波模态，若其传播特性曲线为

k

(

ω

)，在间距为

d

的传感器对下，测试信号中的直达成分可表示为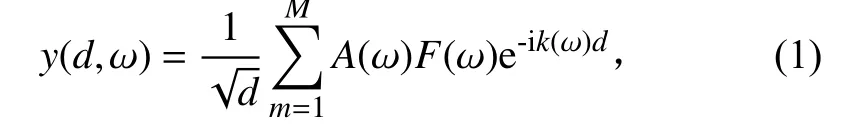

式中：

M

为激发信号的模态数量；

F

(

ω

)和

A

(

ω

)分别表示激励信号的傅里叶表达和幅值调制方程。在多数情况下，高阶模态的激发需要更高频率，因此Lamb 波损伤检测更多采用低阶模态——A0 模态和S0 模态。在Lamb 波的传播过程中可将结构中的损伤视为二次声源，因此，对于任意Lamb 波成分，若信号的测试位置为

L

，超声导波经由损伤位置

d

反射后传递至接收位置

L

，则该二次声源的接收信号可整理为

因此，在测试信号中，Lamb 波的散射模型可简化为直达信号

y

(

t

)、反射信号

s

(

t

)和噪声信号

n

(

t

)的累加，即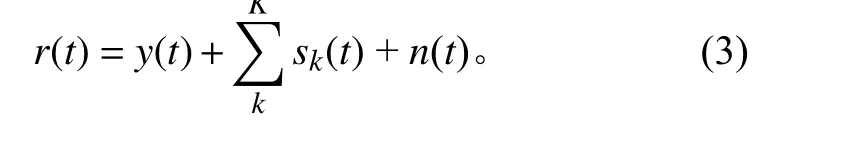

Lamb 波散射模型的建立可为理解Lamb 波的传播机制提供数学表达，无论对于Lamb 波传播特性估计模型的建立，还是损伤的定位成像均具有重要作用。式(3)还是建立Lamb 波稀疏模型的基础。

2 导波频率‒波数域的稀疏重构方法

2.1 超声导波的频率‒波数域稀疏表达

稀疏重构算法的前提在于：若信号可以在某个变化域内稀疏表达，则可通过求解线性约束问题，由少量测量得到较高精度的重构结果。假设自然信号

x

为长度为

N

的一维信号，具有

s

个非零值（稀疏度为

s

）。通过

M

×

N

维的测量矩阵

A

（

M

＜

N

）对自然信号进行测量，忽略测量噪声的情况下，可得到测量信号

y

与自然信号

x

的关系为

y

=

Ax

。稀疏求解的目标是在已知关系矩阵和测量结果的前提下，以稀疏性为约束求解欠定方程组，最后实现原始信号的重构。算法原理如图3 所示。

图3 稀疏重构算法原理示意Fig. 3 Schematic diagram of sparse reconstruction algorithm

Lamb 波的传播特性曲线

k

(

ω

)是其传播的重要特征，在频率‒波数域的表达下，各模态成分的曲线如图4 所示。由图可知，Lamb 波的传播实际由频散曲线调控，且各个模态的频散曲线聚集性高，模态间的分离度强，因此，若信号可在频率‒波数域内实现表达，则其结果一定为稀疏分布的，可满足稀疏重构求解算法的运算前提。由稀疏重构算法模型可知，其关键在于设计测试矩阵。由于测试矩阵取决于Lamb 波的传播模型，根据式(3)可建立Lamb波关于频率‒波数关系的稀疏表达。

图4 铝板中的Lamb 波频散曲线Fig. 4 Lamb wave dispersion curve in aluminum plate

2.2 超声导波的稀疏方程及求解方法

根据式(1)，决定Lamb 波传播信号的关键因素在于传播距离和Lamb 波的频散曲线，因此模型具有2 个未知数。在测试过程中，激励和接收传感器的位置通常可直接获取，因此，在传播数学模型中，对直达波信号，其传播距离可视为已知，仅其频散曲线为未知量。对于多个测试点，其测试信号矩阵

Y

为各个离散点测试信号的集合

Y

=[

r

,

r

,

r

, …,

r

]，对应的传播距离矩阵为

d

=[

d

,

d

,

d

, …,

d

]，则可由式(1)建立测试信号集为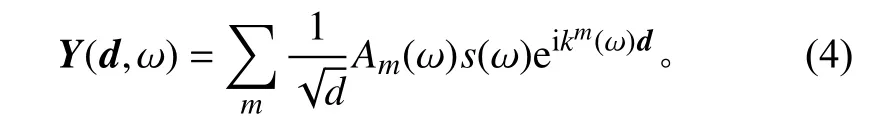

由于无法直接建立频率‒波数的稀疏表达方式，本文采用Lamb 波信号在频率‒波数域内的能量分布作为稀疏矩阵，即在特定的频率‒波数关系下，Lamb 波各个模态的能量会集中在相应的频率‒波数关系曲线附近。因此，可根据Lamb 波的幅值响应建立二维稀疏矩阵

V

(

ω

,

k

)

此时，即可根据Lamb 波的传播模型构建其幅值的稀疏表达方程，其中幅值的频率‒波数域分布表征Lamb 波的传播特性曲线。可通过压缩感知算法求解稀疏方程，其目标求解方程为

由于在稀疏求解过程中，

l

范数的求解比较困难，而

l

范数被证明是

l

范数求解的最优凸近似。因此，通过

l

范数替换求解可极大降低求解难度并保证准确性。本文采用基追踪消噪（basis pursuit denoising, BPDN）对式(8)进行优化求解。

2.3 传播特性结果的脊线追踪

由于测试信号包含非确定性成分且测点有限，求解结果并非完全的稀疏。但主要频率‒波数域表达结果的能量集中在相应的频散曲线附近，因此可通过提取局部最大值来溯源频率‒波数关系曲线。由于激励信号的幅值范围有限，所以仅将可激励的模态及其所在的频率范围作为本文的脊线追踪目标。脊线搜索的主要步骤如下：

1）在有效的波数范围内，选取任意波数

k

，提取该波数下的幅值随频率变化曲线，找出极值点

P

, …,

P

，揭示可激励成分的模态成分数量；2）以极值点位置

P

(

k

,

ω

)为中心，分别沿频率增加和频率减少2 个方向搜索局部最大值；

3）以新搜索的局部最大值为下一次搜索的中心点，重复步骤2），直至覆盖有效搜索范围，此时以像素点幅值与最大幅值比的1%为停止条件；

4）对向上和向下搜索结果进行融合，得到目标模态成分的传播特性估计结果并进行插值，提取频率‒波数关系，计算相速度和群速度曲线。

由上述步骤，可计算得到测试过程中可激发、有效频带范围内的Lamb 波各模态的局部传播特性曲线。此方法相比于二维傅里叶变换方法，可极大地降低对测点数量和高空间采样率要求。

3 测试实验验证

3.1 实验设置

实验采用Nd:YAG 激光器作为超声导波的激励设备，压电片作为接收装置。实验对象为蜂窝夹层复合材料机翼结构，其上下表面均为碳纤维复合材料板，厚度分别为2.5 mm 和1.2 mm，中间层为Nomex 蜂窝芯层，高度为19 mm。激光照射到结构表面，因热弹效应或热蚀效应产生超声Lamb 波。实验采用线性扫描，以1 mm 为步长获取50 组测试信号，形成信号矩阵。由安捷伦示波器以10 MHz的采样频率采集时长为1 ms 的测试信号。实验设置如图5 所示。

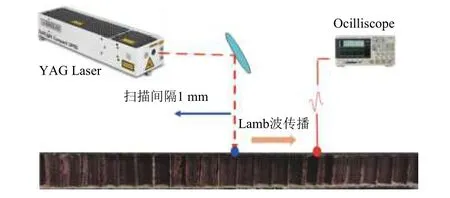
图5 激光激励超声导波测试实验设置Fig. 5 Experimental setup of laser-excited supersonic Lamb wave

3.2 数据预处理

激光激励的超声Lamb 波信号可视为脉冲激励下的结果，其带宽大但主要能量集中在低频。实验中，针对蜂窝夹层复合材料结构，其激光激励的超声导波高频信号由于衰减幅值迅速降低，且信号中位移占优的A0 模态可激发频带位于低频，因此在多重因素作用下的有效信号频带在150 kHz 以下。图6 为传感器1 接收信号示例，包括Lamb 波时域信号及其频谱。

图6 传感器1 接收信号示例Fig. 6 Example signal from sensor No. 1

为了降低强幅值调制的影响和高频噪声带来的干扰，对激光激励信号进行滤波处理，提取有效频带([5, 125] kHz)内的超声Lamb 波信号；并对窄带滤波后的信号进行去直流处理，以进一步降低直流信号成分的干扰，得到结果如图7 所示的Lamb波信号。

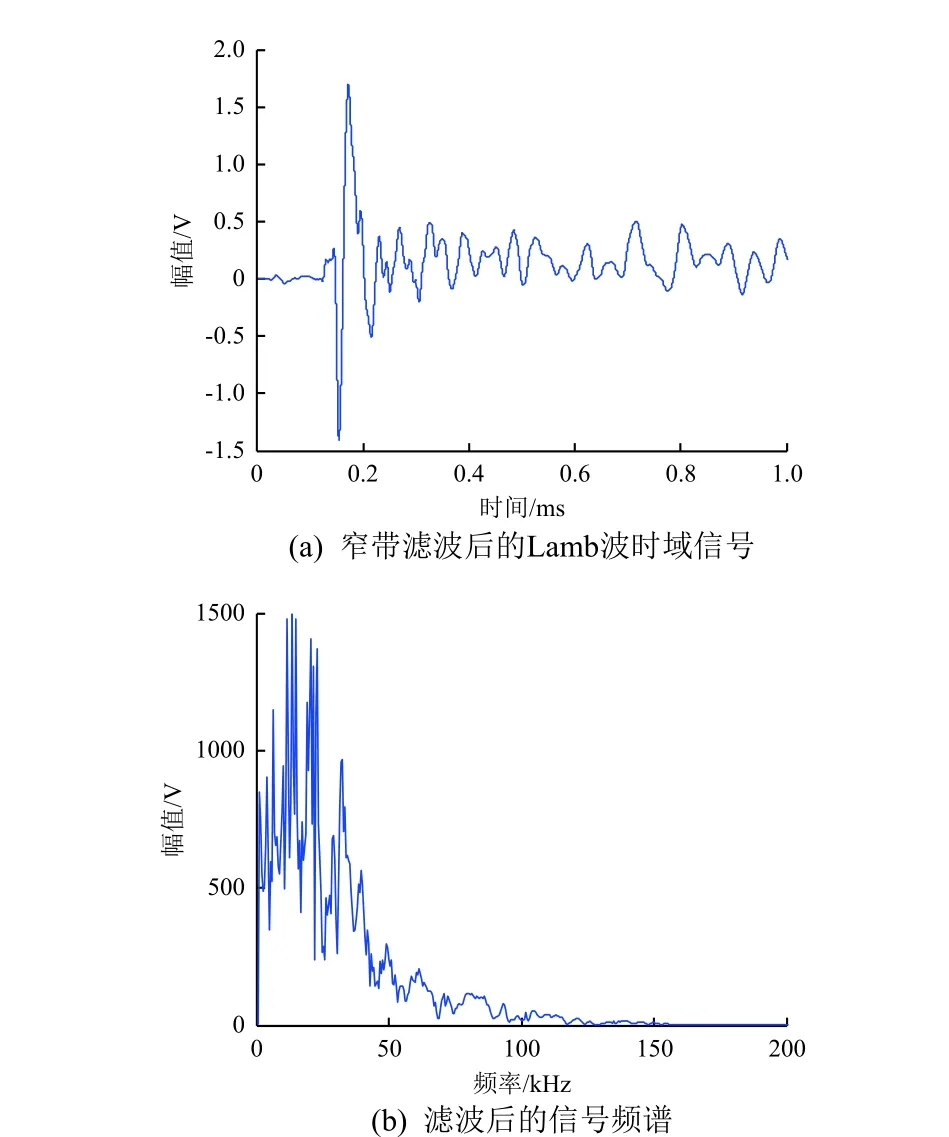
图7 预处理后的Lamb 波信号Fig. 7 Lamb wave signals after pre-processing

3.3 实验结果

采用50 组间隔1 mm 扫描的信号作为测试信号，通过稀疏重构算法求解得到的Lamb 波频率‒波数域表达结果如图8 所示。

图8 频散曲线估计结果Fig. 8 Estimated results for the dispersion curve

由于反射信号成分和噪声的干扰，频率‒波数域的原始重构结果中出现微弱干扰成分；对该重构结果进行脊线搜索，搜索范围为[5, 125] kHz，得到局部幅值最大处的频率‒波数关系，从而提取得到频散曲线；采用二次样条插值方法对脊线进行插值细化，则可得到A0 模态成分的频散曲线。

由于信号成分中波包以群速度传播，可以通过波包的传播距离和到达时延对求解A0 模态传播速度曲线进行验证。群速度

C

可通过频率‒波数的求导获得，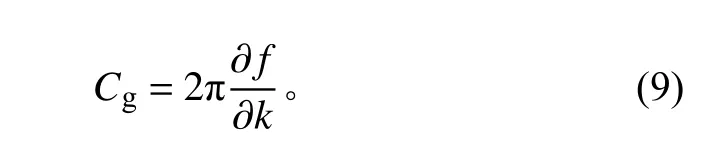

对测试信号进行窄带滤波，通过求解的频散曲线分别计算40～90 kHz 下的Lamb 波相速度和群速度值，得到部分频点下的估计结果，如表1 所示。

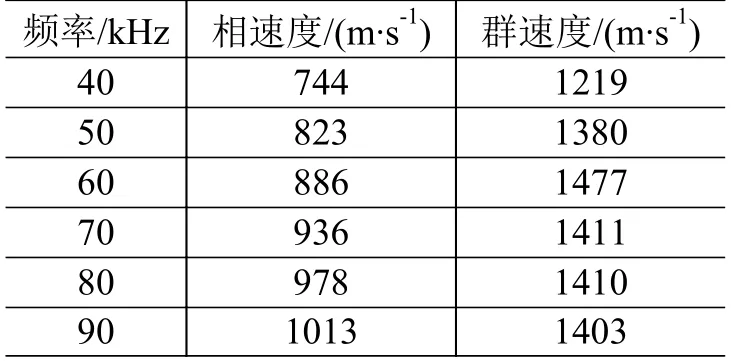
表1 部分频率下的传播速度结果Table 1 Estimated velocities for selected frequencies

由上述结果可知，通过稀疏重构算法可有效重构可激励模态成分的频散曲线，由于激光器产生的Lamb 波以热蚀效应为主，所以Lamb 波传播过程的振动中离面位移占优，在测试信号中A0 模态的成分要远强于S0 模态信号，使得重构结果中仅A0 模态信号可见。因此，本文所提方法仅可重构可激发超声Lamb 波模态信号。此外，由于输入稀疏模型的参数中仅匹配了入射成分的坐标位置，所以无法重构反射成分。相较而言，实验求取的传播特性结果能更准确地贴合实际工况和服役环境，因此对于损伤的定位成像、缺陷的定量评估等更加准确。

4 结束语

为提高实验求解Lamb 波传播特性的精度和最小化测试信号数量，本文提出基于稀疏重构算法的Lamb 波传播特性估计方法。以激光器作为非接触超声Lamb 波的激励，对蜂窝夹层复合材料结构进行波场线性扫描，捕获结构的状态信息。通过构建Lamb 波的传播数学模型，以Lamb 波的频率‒波数域表达的稀疏性为约束，求解得到的稀疏表达蕴含了Lamb 波的传播特性信息。在局部最大值搜索下，实现了目标成分的脊线提取，从而获得了Lamb波的频散曲线。进一步，可计算得到目标模态成分的相速度和群速度，实现复杂结构中的Lamb 波传播特性的准确求取。本文提出的方法可有效解决蜂窝夹层复合材料航空航天装备结构中Lamb 波传播特性准确求解的难题，在提升损伤检测能力和定位成像精度方面具有重要应用前景。