曲线U型钢腹板组合箱梁剪力滞效应研究

王连广,黄学达,陈力栋

(东北大学资源与土木工程学院,辽宁 沈阳 110819)

利用曲线U型钢梁与混凝土板连接成的组合梁,具有承载力高、稳定性好等优点[1]。Ji Wei[2]、刘旭政等[3]通过研究得到宽跨比对箱梁剪力滞系数的影响较大;赵虎等[4]研究了波形混合多箱桥剪力滞效应,发现箱梁顶板和混凝土板腹板剪力滞效应较大;张元海等[5-6]使用初参数法分析薄壁箱梁的剪力滞效应,给出了方程的初参数解;邬晓光等[7-9]对剪力滞效应进行理论分析,得到了剪力滞影响下梁的应力方程。还有学者基于薄壁杆件理论对曲线箱梁进行了研究[10-11]。E.Yamaguchi等[12-15]分析了宽跨比、荷载作用方式及类型等参数对应力和变形的影响；H.Amoushahi等[16]利用有限条法预测了箱型梁不同荷载下的屈曲荷载。王连广[17]选择不同次数的抛物线型翘曲位移函数,得到了钢与混凝土组合箱梁的应力解析解,结果表明二次型剪滞位移函数更符合实际。

目前,国内外对钢与混凝土组合梁的研究主要针对直线组合梁的内力、变形等,而对于曲线组合梁的剪力滞效应研究较少。基于此,笔者基于能量法创建曲线组合梁的剪力滞效应控制微分方程,选用加权余量法分析曲线U型钢腹板组合箱梁在不同抛物线和余弦函数型剪滞翘曲位移函数下的应变规律;选用差分法计算分析影响U型钢腹板组合箱梁剪滞效应的主要参数,最终得到各参数对曲线U型钢腹板组合箱梁的影响曲线。

1 基于抛物线型位移函数的曲线组合梁剪力滞效应

1.1 剪力滞翘曲位移函数

进行分析时采用如下基本假定[18]:①U型钢腹板与混凝土顶底板竖向贴合;②剪力滞效应只在竖向弯曲中计入;③忽略混凝土顶底板的竖向挤压应变和横向应变;④处于弹性工作状态;⑤均为线弹性材料。

曲线U型钢腹板组合箱梁截面简化示意图如图1所示。

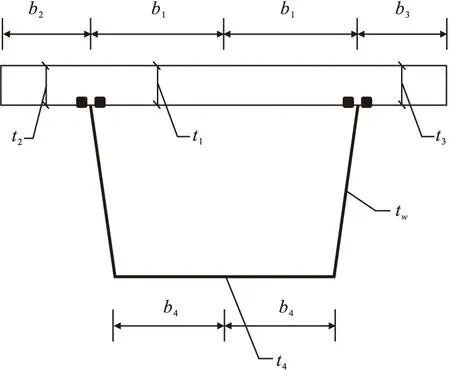
图1 U型钢腹板组合箱梁截面尺寸示意图Fig.1 Section size diagrams of U-shaped steel web composite box girder

曲线U型钢腹板组合箱梁在荷载作用下,上下翼板也会产生剪力滞效应,且由于曲率的存在,其剪力滞效应分析与直线梁不同。笔者在现有曲线U型钢腹板组合效应剪力滞效应研究的基础上,求得剪力滞效应的通用表达式,在此基础上分析其他组合结构形式的剪力滞效应。剪力滞翘曲位移函数如下:

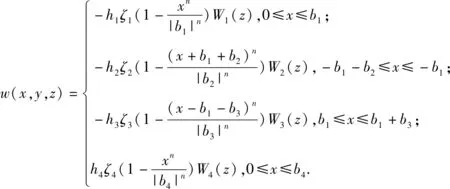
(1)

式中:b1表示混凝土顶板宽度的一半;b2表示混凝土上部外悬臂板宽度;b3表示混凝土上部内悬臂板宽度;b4表示钢底板宽度的一半;h1、h2、h3、h4分别表示各板块形心至截面形心的距离;W1(z)、W2(z)、W3(z)、W4(z)分别表示各板块的纵向位移剪切转角差函数;ζ表示翼缘板宽度和边界条件不同下的修正系数[19],ζ1=ζ4=1,ζ2=(b2/b1)2,ζ3=(b3/b1)2。

由于受曲率的影响,曲线组合箱梁的几何方程由文献[20]给出:

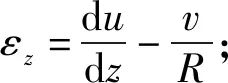
式中:u、v、w分别表示x、y、z方向的位移;φ为扭转角。

1.2 组件势能

在考虑应变能时,忽略钢箱曲线组合梁中钢梁剪切变形,但腹板部分在抵抗弯曲形中不可忽略.根据最小势能原理可得:

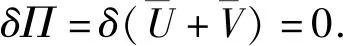
(2)

体系总势能如下:

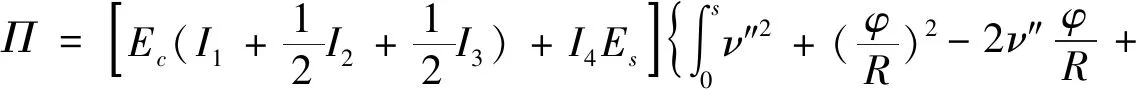
(3)

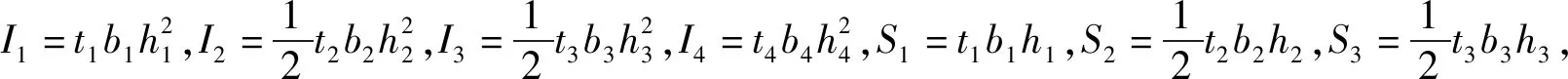
S4=t4b4h4。

1.3 控制微分方程

根据最小势能原理可知,δΠ=0,考虑弯扭、剪力滞后以及界面滑移耦合的控制微分方程。

微分方程如下:

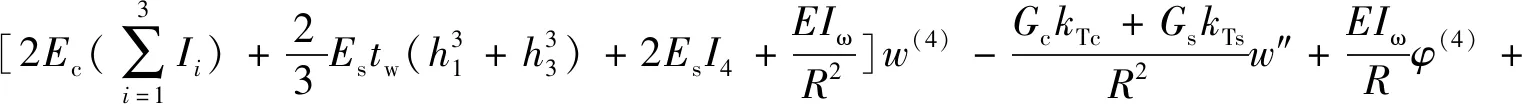
(4)

(5)

(6)

(7)

(8)

边界条件如下:

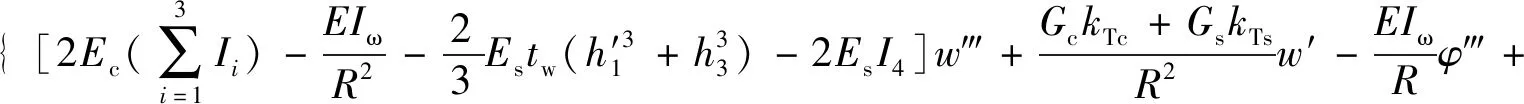
(9)

(10)

(11)

(12)

(13)

(14)

(15)

1.4 控制微分方程解析

上述平衡微分方程是含有多个位移函数耦合的线性高阶常系数微分方程,难以求得闭合解,因此考虑数值解代替。加权余量法是数值计算中应用较为广泛的一种方法,采用加权余量法可求得混凝土顶底板不同宽度处的正应力值。

顶板应力:

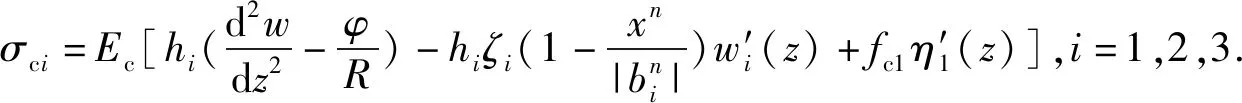
(16)

底板应力:

(17)

2 基于余弦函数型位移函数的曲线组合梁剪力滞分析

2.1 剪力滞翘曲位移函数

基于余弦函数型位移函数的曲线U型钢腹板箱梁进行分析时的基本假定为①混凝土顶底板与U型钢腹板竖向贴合；②剪力滞效应只在竖向弯曲中计入；③忽略混凝土顶底板的竖向挤压应变和横向应变；④组合箱梁处于弹性工作状态；⑤均为线弹性材料。梁截面示意图同第1节所设。

剪力滞翘曲位移函数如下:

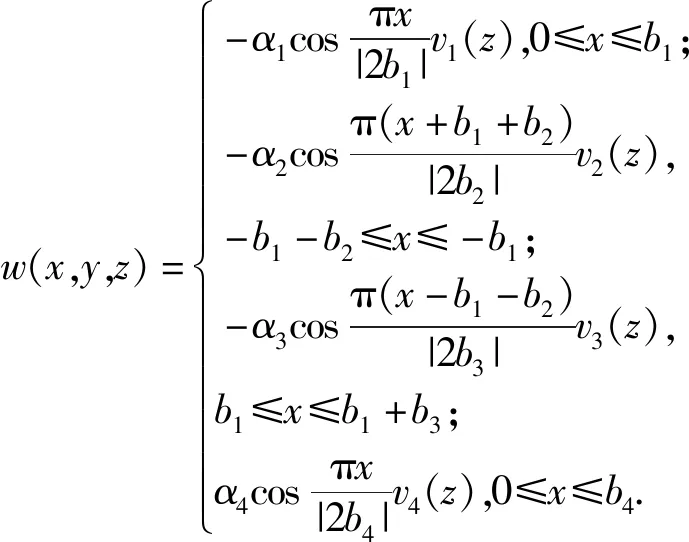
(18)

式中:α1=α4=1,α2=(b2/b1)2,α3=(b3/b1)2;

vi(z)表示翼板剪切变形最大位移差函数。

2.2 控制微分方程解析

采用加权余量法可求得混凝土顶底板不同宽度处的正应力值。

顶板应力:

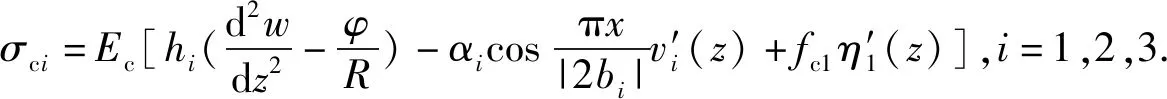
(19)

底板应力:

(20)

3 算例分析

考虑不同的剪滞翘曲位移计算所得的应变会产生差异,截面形式的不同会导致计算得到的应变差异不同,故对不同截面的位移函数进行分析。曲线U型钢腹板箱梁截面示意图如图2所示。

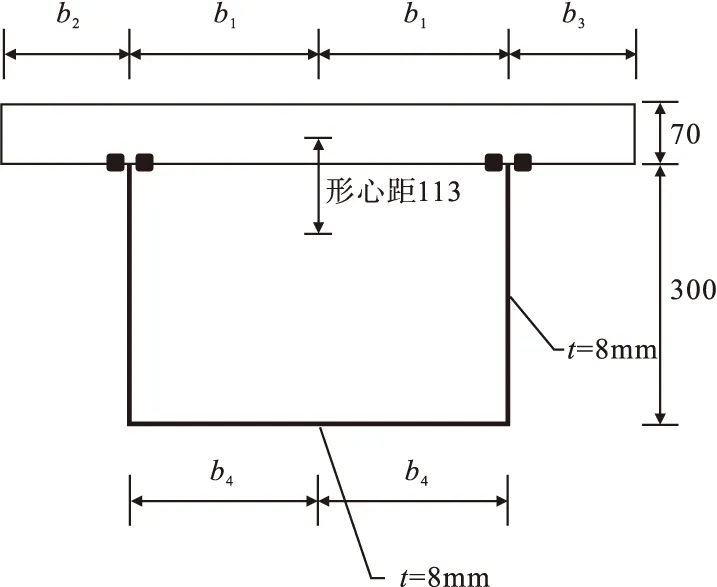
图2 曲线U型钢腹板组合梁尺寸简化示意图Fig.2 Section size diagrams of curved U-shaped steel web composite box girder

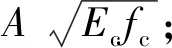
令W1=W2=W3=W4=W(z),计算得:Kd=448.37 N/mm。中和轴位置:h1=h2=h3=183 mm,h4=217 mm,Gc=1.44×104MPa,Gs=7.69×104MPa,fc=-0.443,fs=0.557。扇形惯性矩:EIw=1.67×1021mm6。组合梁抗扭惯性矩:GckTc+GskTs=1.152×1014N·mm2。曲线梁曲率半径R=50 m,计算跨度l=5 m,均布荷载为80 N/mm,qn=102 N/mm,ζ1=ζ4=1,ζ2=ζ3=0.44。

取n=2、n=3、n=4、n=5、n=6,以及取剪滞函数按余弦变化后解方程,计算结果见表1。

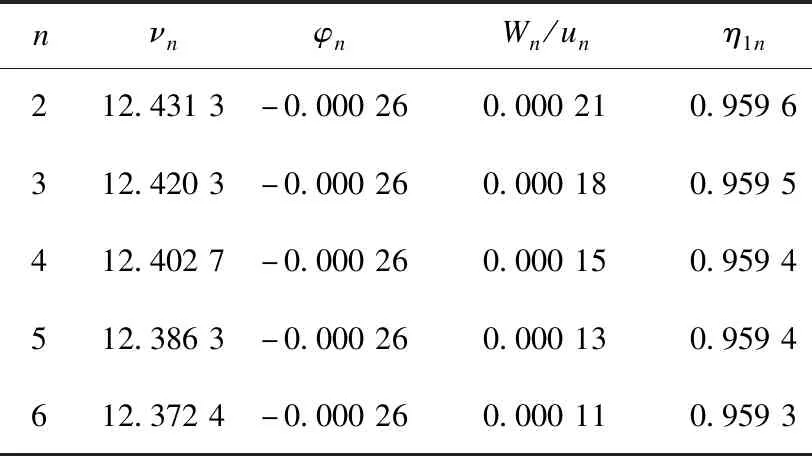
表1 曲线U型钢腹板箱梁计算结果Table 1 Calculated results of curved U-shaped web box girder

跨中截面不同宽度处顶底板正应变曲线如图3、图4所示。

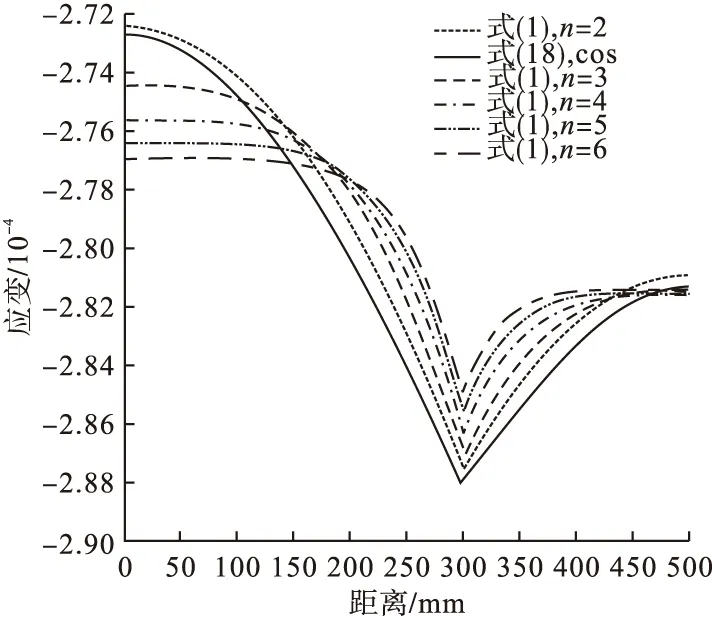
图3 顶板位移函数对比分析Fig.3 Comparative analysis of displacements function of roof

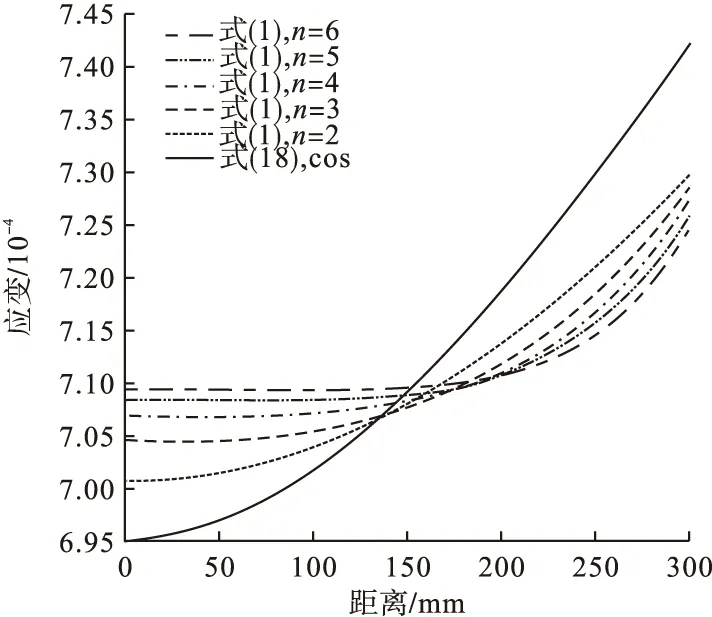
图4 底板位移函数对比分析Fig.4 Comparative analysis of displacement function of bottom plate

由图可见,在顶板各位置处,按n次抛物线规律变化的考虑剪力滞效应的应变曲线差别不大,按余弦函数变化得出的曲线与n次抛物线变化得出的曲线较接近,所有曲线中最大和最小处仅相差3×10-6。因此剪滞翘曲位移变化形式对顶板的受力分析影响不大,在工程实例中可任取一种剪滞翘曲位移变化规律分析,不影响精度。但在底板上所有曲线的最大和最小应变差值为1.8×10-5,如需较高分析精度则同样需通过实验或模拟确定最适曲线。

4 剪力滞效应参数分析

4.1 混凝土板厚影响

参数与第3节中U型钢截面相同,曲率半径取R=50 m,跨度取l=5 m,将曲线组合梁分为16段,则有17个实节点,两个虚节点,编号见图5,其中0和18号为虚节点。

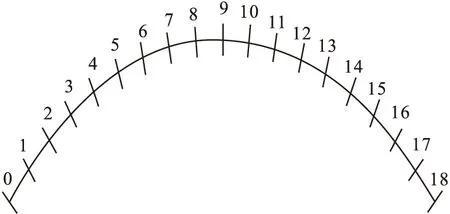
图5 差分网格示意图Fig.5 Schematic diagram of differential grid

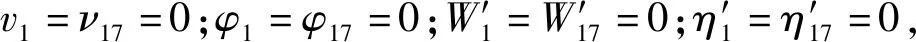
代入微分方程得:

A1x=b1.

(21)

式中:A1=[A11A21A31A41]T;b1=[80…80…0…0]T;x=[ν0ν1…ν18φ0φ1…φ18W0W1…W18η0η1…η18]T(共76个未知数)。

A11为第一个控制微分方程的差分形式分别代入截面参数后得到的分块矩阵。取60 mm板厚为示例,15个差分点可以列出15个式子,阶梯状分布。A21、A31、A41同理,不再赘述。

将第1、第17节点处的边界条件代入方程可得如下矩阵:

A2x=b2.

(22)

式中:

b2=[0 0 0 0 0 0 0 0 ]T。

代入边界条件得:

A3x=b3.

(23)

式中:A3为四个边界条件的差分表达式,代入截面参数所得矩阵b3=[0 0 0 0 0 0 0 0 ]T。

将3个表达式合并可得:

[A1A2A3]Tx=[b1b2b3]T.

(24)

解得每个节点的竖向位移ν、转角φ、剪滞函数值W以及滑移量η,进而求得每个节点处的应变和有效宽度系数β随板厚变化趋势(见图6)。

从图6可以看出,当保持组合截面的其余参数不变,只改变混凝土顶板厚度,得到的顶板有效宽度系数随板厚的增加而增加,但增加幅度非常小,在板厚增加42%的情况下有效宽度系数仅提高了2%,说明顶板厚度不是影响曲线U型钢腹板组合箱梁的主要因素。

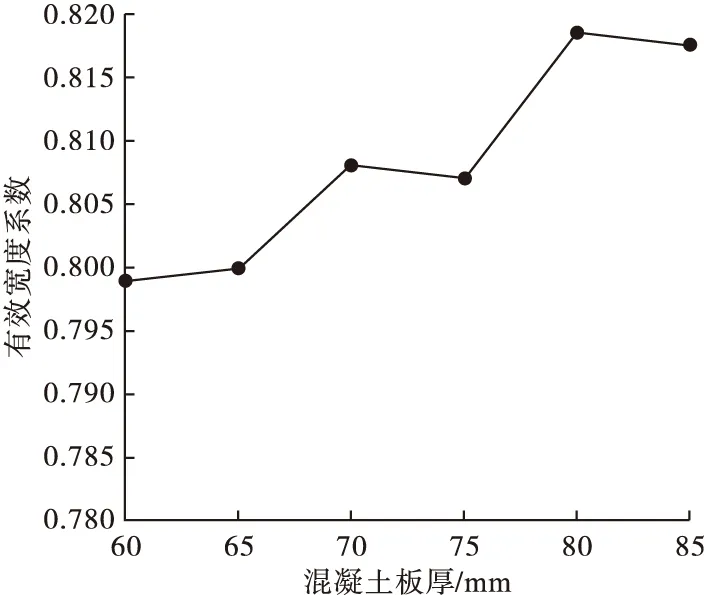
图6 有效宽度系数随顶板厚度变化曲线Fig.6 Curve of effective width coefficient with the change of roof thickness

4.2 混凝土强度等级影响

计算过程与板厚对有效宽度系数的影响分析类似,此处不再赘述。当混凝土强度等级分别取C40、C45、C50、C55、C60、C65时,顶板有效宽度系数变化曲线如图7所示。

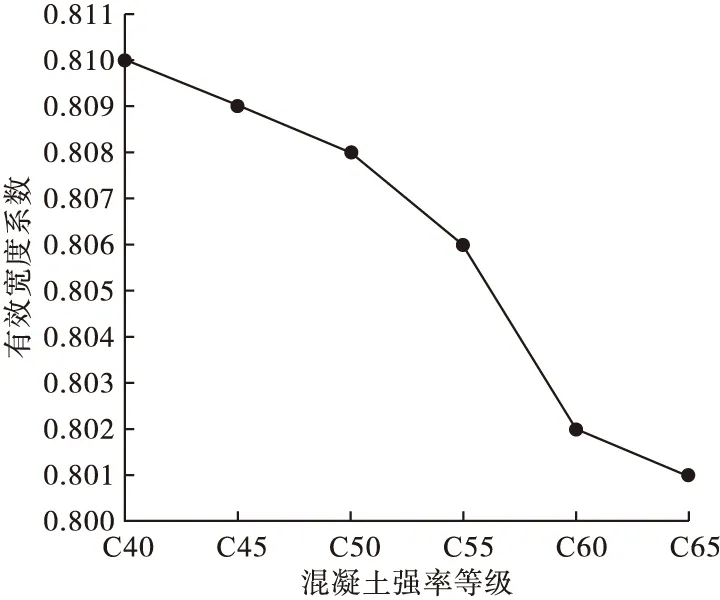
图7 有效宽度系数随混凝土强度等级变化曲线Fig.7 Curve of effective width coefficient with the change of concrete strength grade

从图7可以看出,当混凝土强度等级从C40增加到C65时,有效宽度系数仅从0.81下降至0.801,可见混凝土强度等级的增加使有效宽度系数有所降低,但影响非常小。

4.3 界面滑移刚度影响

界面滑移刚度从336 N/mm 增加到1 345 N/mm,有效宽度系数变化曲线如图8所示。

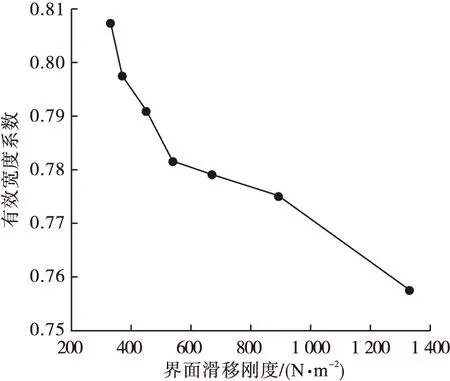
图8 有效宽度系数随界面滑移刚度变化曲线Fig.8 Curve of effective width coefficient with the change of interface slip stiffness

由图8可以看出,当滑移刚度从336 N/mm增加到1 345 N/mm时,混凝土顶板有效宽度系数明显减少。界面滑移刚度的增加虽然可以使组合梁拥有更好的整体性,也会使剪力滞效应发生明显变化。

4.4 曲率影响

跨长不变,曲率半径由20 m增加至80 m,混凝土顶板有限宽度系数变化曲线如图9所示。

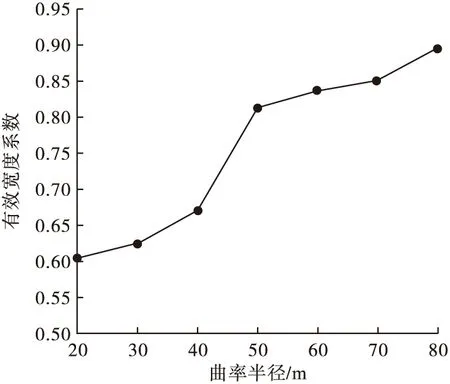
图9 有效宽度系数随曲率半径变化曲线Fig.9 Curve of effective width coefficient with the change of radius of curvature

由图9可以看出,在曲线U型钢腹板组合梁中,顶板有效宽度系数随曲率半径的增大而增大。即随着曲梁弯曲程度的减缓,剪力滞效应下降非常明显。

4.5 悬翼比影响

悬臂板宽度由200 mm增加至400 mm时,悬翼比由0.67增加到1.33(悬翼比为悬臂板宽度与顶板宽度一半的比值)。顶板有效宽度系数变化曲线如图10所示。

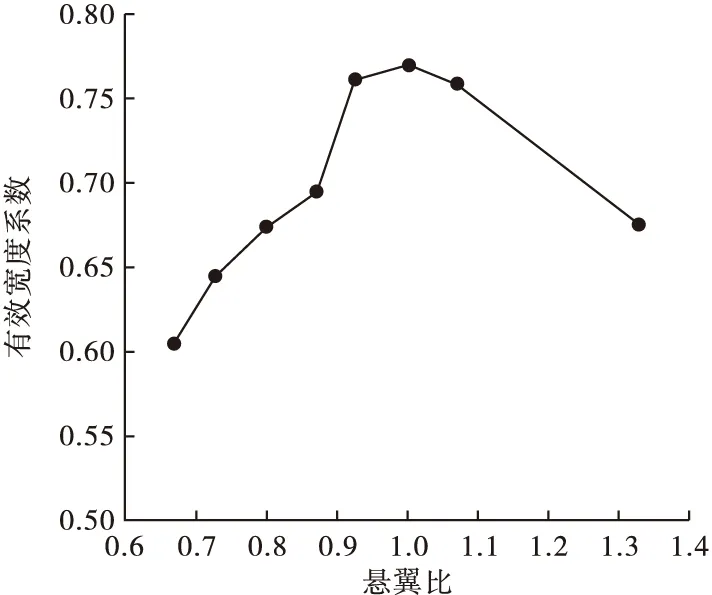
图10 有效宽度系数随悬翼比变化曲线Fig.10 Curve of effective width coefficient with the change of cantilever-wing ratio

由图10可以看出,在悬翼比小于1时,有效宽度系数随翼板的增大而增大;但当悬翼比大于1时,有效宽度系数随翼板的增大而减小。反应到曲线梁实际受力当中,即当悬臂板宽度不大于顶板宽时,随着悬臂板宽度增加,截面惯性矩减小从而使顶板正应力整体减小,与腹板相连顶板位置的正应力减小值较其余部位小,从而使有效宽度系数减小;但当悬臂长度大于1倍顶板宽度时,有效宽度系数也迅速减小。

4.6 跨宽比影响

跨长从4 m增加至9 m时,顶板有效宽度系数变化曲线如图11所示。从图11可以看出,当跨宽比l/b增大时,有效宽度系数显著增加;当跨宽比增加1.25倍时,有效宽度系数增加了37%。说明简支曲线组合梁的剪力滞效应随跨度的增加而减小,宽跨比对曲线梁剪滞效应影响较大。

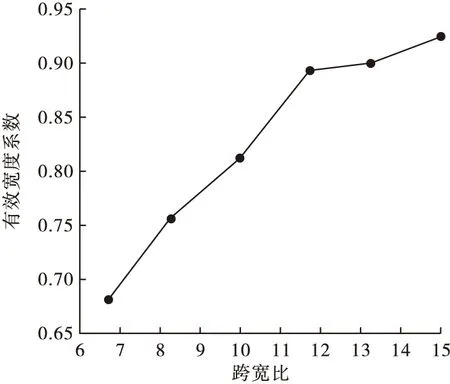
图11 有效宽度系数随跨宽比变化曲线Fig.11 Curve of effective width coefficient with the change of width-span ratio

5 结 论

(1)U型钢腹板组合箱梁顶板应变曲线随剪力滞翘曲位移函数的不同选择差别不大,但底板的应变曲线差别较大。

(2)混凝土顶板厚度和混凝土强度等级对顶板的剪力滞效应影响不大;顶板有效宽度系数随滑移刚度的增加而减小,随曲率半径的增加而增加,随跨宽比的增加而增加。当悬翼比小于1时,剪力滞效应随悬翼比增加而减小,当悬翼比大于1时则相反。