弹性边界对高速列车车窗声辐射特性的影响研究

朱荟吉，齐玉文，徐佳明，邓铁松，金学松*,

弹性边界对高速列车车窗声辐射特性的影响研究

朱荟吉1，齐玉文2，徐佳明2，邓铁松1，金学松*,1

（1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.中车长春轨道客车股份有限公司，吉林 长春 130062）

为研究高速列车车窗在点激励下的声辐射特性，基于Hamilton原理和声学Rayleigh积分建立了弹性边界条件下车窗的有限元－边界元耦合模型，模型中将弹性边界简化为沿车窗四周连续分布的平动弹簧和转动弹簧。利用矩形板在经典边界条件下的模态分析结果、无限大板的声辐射验证了模型的正确性。基于验证后的模型，分析了边界支撑刚度对车窗声辐射的影响，研究了车窗声辐射随边界阻尼的变化规律。研究结果表明，边界平动刚度对车窗声辐射的影响较转动刚度显著；当平动刚度小于1×103N/m时，车窗的声辐射与无限大板的结果相似；当平动刚度在1×103～1×106N/m间变化时，声辐射出现明显峰值，且随刚度迅速变化，这些峰值由车窗的模态引起；当平动刚度大于1×106N/m时，车窗的声辐射随刚度趋于稳定；提高边界阻尼有助于降低车窗在辐射峰值附近的声辐射水平，但作用有限，其中，由复平动刚度产生的边界阻尼比复转动刚度产生的边界阻尼对车窗声辐射的影响大。

高速列车；车窗；弹性边界；有限元；边界元；声辐射

随着高速列车的快速发展，车内噪声问题日益凸显，而车内噪声作为衡量乘车舒适度的重要指标之一，已成为影响高速列车向更高速、更友好发展的关键因素之一[1-2]。高速列车车窗作为车体的重要部件之一，通过橡胶等弹性元件安装于车体上，车外振动和噪声激励车窗向车内辐射噪声[3-4]，研究弹性边界条件下车窗的振动声辐射特性对控制车内噪声具有重要意义。

高速列车车窗声振特性（振动声辐射和隔声）的研究甚少[5-11]。其中，Baldanzini等[5]研究了双层车窗中弯曲波的传递特征，确定了高速列车车窗SEA模型的关键参数。Yang[6]结合遗传算法对双层车窗的几何参数进行了优化。张玉梅等[7-8]考虑边界条件的影响，基于波动法和模态叠加法[9-10]，建立了高速列车车窗的双板空腔隔声模型，分析了车窗厚度、空腔厚度和空腔阻尼等参数对车窗隔声的影响。Xu等[11]利用SEA对比分析了高速列车单层车窗、双层车窗及中空双层车窗的隔声性能，研究了车窗与窗框间的密封材料对车窗隔声的影响。

高速列车车窗呈矩形状，对高速列车单层车窗的声振特性研究实际上就是对弹性边界条件下矩形板声振特性的研究，研究方法主要包括解析法[12-13]、能量法[14-15]和有限元－边界元法（FE-BE）[16-17]。其中，解析法要求矩形板至少一边简支，收敛速度慢；能量法的关键之处在于容许位移函数的构造，要求容许函数适合结构的实际振动和满足边界支撑条件，同时要求外载荷也能表示成容许函数的形式，在实际工程应用中寻找既收敛又满足这些要求的容许函数往往存在一定的困难；而有限元－边界元法通用性强，不受边界条件和外载荷形式的限制，当单元尺寸足够精细时，数值解收敛于问题的精确解。

因此，本文将采用通用性强的有限元－边界元法来展开高速列车车窗在弹性边界条件下的声辐射特性研究。基于薄板理论，利用Hamilton原理建立高速列车车窗在弹性边界条件下的FE模型，基于声学Rayleigh积分建立车窗两侧声学域的BE模型，结合车窗与流体的边界耦合条件，建立弹性边界条件下车窗的耦合FE-BE声振预测模型，利用经典边界条件下矩形板的模态分析结果和无限大板的声辐射验证耦合模型的正确性，利用验证后的FE-BE耦合模型来研究边界支撑刚度和边界阻尼对车窗声辐射的影响。

1 高速列车车窗的耦合FE-BE模型

高速列车车窗的声振耦合FE-BE模型包括弹性边界下车窗的FE模型、车窗两侧声学域的BE模型及FE模型与BE模型的耦合模型。

1.1 弹性边界下车窗的FE模型

高速列车车窗为典型的矩形薄板，以下基于薄板理论，利用Hamilton原理来建立弹性边界下矩形板的FE模型。弹性边界下矩形薄板如图1所示，长2，宽2，四边受弹性支撑，它们被简化为沿四边连续均匀分布的出平面平动弹簧和转动弹簧。将四边分别记为Γ-a、Γ+a、Γ-b和Γ+b，对应的平动和转动弹簧刚度分别为k-a和k-a、k+a和k+a、k-b和k-b、k+b和k+b，平动弹簧刚度的单位为N/m，转动弹簧刚度的单位为N/rad。

图1 弹性边界矩形板示意图

根据Hamilton原理，弹性边界条件下矩形板的动能和势能应满足[17]：

式中：为薄板的动能，J；为薄板的势能，J；为薄板的变形势能，J为由弹性边界产生的势能，J；包括和。、和的计算公式为[17]：

式中：为薄板的出平面位移，m；为薄板的应力－应变矩阵；为薄板的应变－位移矩阵；为薄板的面积，m2。

基于Kirchoff薄板理论，将矩形板出平面位移表示成节点位移和插值函数的形式，然后依次代入式（2）、式（3）、式（4）和式（1）可得弹性边界下矩形薄板的FE方程为：

为角频率，rad/s；K为矩形板变形势能产生的刚度矩阵，N/m；K为矩形板边界弹性支撑产生的刚度矩阵，N/m或N/rad。

1.2 车窗两侧声学域的BE模型

在研究板件结构的振动声辐射时，板件往往置于无限大障板中，板两侧声学域为无限半空间，声场分布特性可由声学Rayleigh积分来计算[20]：

利用式（6）计算声学域与矩形板接触边界上的节点声压，可得声学域的BE模型为：

1.3 耦合的FE-BE模型

矩形板在外力激励下发生振动，向两侧声学域辐射声波p1和p2，与两侧声学域相互作用。矩形板与两侧声学域的耦合边界条件包括：①两侧声压作为外部激励作用于矩形板；②在接触边界上，矩形板的法向速度与声学域的法向速度相等。结合这两个耦合条件以及式（5）、式（7），可得弹性边界下矩形薄板与两侧声学域耦合的FE-BE模型为：

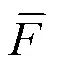
2 验证

本节以一块长1 m、宽1 m及厚6 mm的铝板ANSYS模态分析结果来验证本文的FE模型，以无限大铝板的声辐射来验证耦合FE-BE模型。铝板的材料参数如表1所示。

表1 铝板材料参数

2.1 模态分析

将矩形板边界的平动和转动刚度分别或同时设为0或无穷大，可得到自由、简支和固支等经典边界条件。由本文计算的铝板在经典边界条件下的模态频率与ANSYS结果的对比如表2所示。由表2可知，在经典边界条件下，本文得到的模态频率与ANSYS的结果误差在0.5%以内，说明本文建立的弹性边界矩形薄板FE模型是准确有效的。

表2 铝板在经典边界下的模态频率

2.2 声辐射

当单位简谐力垂直作用于矩形板面中心时，矩形板在简支和固支条件下向一侧声场的辐射声功率如图2所示，同时给出了无限大板的声辐射结果。

图2 简支和固支条件下铝板声辐射与无限大板的对比

由图可知，矩形铝板边界支撑刚度使其在刚度控制区的声辐射比无限大板的结果大；在质量控制区，矩形铝板的模态作用使其声辐射较无限大板的结果略大，但整体走势保持一致；在吻合控制区（临界频率以上，约2000 Hz以上），二者的声辐射吻合较好。

通过与商业软件ANSYS的模态分析结果、无限大板声辐射的对比，验证了弹性边界矩形板FE-BE耦合模型的正确性，该模型将在下一节用于某型高速列车的声辐射特性分析。

3 某型高速列车车窗的声辐射特性研究

某型高速列车的车窗长2＝1 m、宽2＝0.7 m、厚＝4 mm，材料参数如表3所示。以下将验证后的弹性边界矩形板FE-BE模型应用于该高速列车车窗，研究边界支撑刚度和边界阻尼对车窗声辐射的影响。后文中的声辐射结果均为单位简谐力垂直作用于车窗中点、车窗向一侧声场辐射的声功率。值得注意的是，边界出平面平动刚度的变化范围为1×100～1×108N/m；边界转动刚度的变化范围为1×100～1×105N·m/rad；因为当平动和转动刚度超出上述取值范围时，车窗的声辐射随刚度的变化不明显，趋于稳定，相应结果未在后文中列出。计算频率范围为10～1000 Hz，这是因为我国高速列车车内噪声的主要频段集中在630 Hz左右的中低频[18-19]；而且边界支撑条件只影响高速列车车窗中低频的声振特性。

表3 某型高速列车车窗材料参数

3.1 边界支撑刚度对声辐射的影响

在不考虑边界阻尼的条件下，图3列出了转动刚度分别为1×100N·m/rad、1×102N·m/rad和1×105N·m/rad时，车窗的声辐射随平动刚度的变化规律。由图可知，在各转动刚度条件下，辐射声功率曲线随平动刚度的变化趋势基本一致，当平动刚度大于约1×103N/m时，振动声辐射曲线在10～1000 Hz内开始出现明显峰值；当平动刚度小于约1×103N/m时，车窗的振动声辐射曲线峰值不明显，可近似为无限大板的声辐射，这是因为当边界平动刚度很小时，车窗边界近似发生自由出平面运动；当平动刚度在 1×103～1×106N/m间变化时，车窗低频声辐射受平动刚度的影响最显著，低频（约小于 500 Hz）辐射峰值随平动刚度的增加而迅速向高频移动，这是因为车窗在刚度控制区（约10～200 Hz）的声辐射和低频模态受边界平动刚度的影响很大；当平动刚度大于1×106N/m时，声辐射随平动刚度的变化不明显，趋于稳定，这是因为车窗边界的出平面位移基本被较大的平动刚度固定。

图3 边界平动刚度对车窗声辐射的影响

与图3类似，图4给出了在不考虑边界阻尼的条件下，平动刚度为1×100N/m、1×103N/m和1×108N/m时，转动刚度对车窗声辐射的影响。

图4 边界转动刚度对车窗声辐射的影响

由图可知，当平动刚度大于约1×103N/m时（平动刚度小于1×103N/m的结果与图4（a）相似，此处未列出），振动声辐射曲线在10～1000 Hz内开始出现明显的峰值；当平动刚度小于约1×103N/m时，车窗的振动声辐射曲线近似为一条直线，可以看成无限大板的辐射声功率。当出现明显的振动声辐射峰值后（图4a和图4c），在不同平动刚度条件下，随转动刚度的增加，峰值频率逐渐变大，但变化速率较随平动刚度的变化速率（图3）慢，这说明车窗四周转动刚度对声辐射的影响小于平动刚度的影响。

3.2 边界阻尼对车窗声辐射的影响

车窗四周的边界阻尼以复刚度的形式体现：

为分别研究由复平动刚度和复转动刚度产生的边界阻尼（阻尼损耗因子分别取为0、0.01、0.1和1）对车窗声辐射的影响，分别固定平动刚度为1×108N/m或转动刚度为1×105N·m/rad，变化另一复刚度。

图5给出了转动刚度为为1×105N·m/rad，由复平动刚度产生的边界阻尼对车窗声辐射的影响。由图可知，当平动刚度较小时（图5a），由于边界阻尼与边界刚度成正比，边界阻尼对车窗声辐射的影响可忽略不计；当平动刚度居中时（图5b），当边界阻尼大于0.1时，边界阻尼才对车窗的低频声辐射产生显著影响，增加边界阻尼能有效抑制车窗在低频辐射峰值（模态频率）附近的辐射声功率；随平动刚度进一步增加，以致于车窗四周不产生位移时（图5c），边界阻尼对车窗振动声辐射几乎不产生影响。

与图5类似，图6给出了平动刚度为1×108N/m时，由复转动刚度产生的边界阻尼对车窗振动声辐射的影响。对比图5和图6可知，由复转动刚度产生的边界阻尼对车窗声辐射的影响小于由复平动刚度产生的阻尼的影响。由图6

可知，当转动刚度较小（图6a）和较大（图6b）时，由复转动刚度产生的边界阻尼对车窗的声辐射影响很小，可忽略不计，原因与图5（a）和（b）保持一致；当转动刚度居中时（图6c），边界阻尼损耗因子大于1时才对结构的振动声辐射产生影响，并增加边界阻尼能有效抑制车窗在低频模态频率附近的振动声辐射水平。

图5 由复平动刚度产生的边界阻尼对车窗声辐射的影响（转动刚度为1×105 N·m/rad）

图6 由复转动刚度产生的边界阻尼对车窗声辐射的影响（平动刚度为1×108 N/m）

4 结论

本文以高速列车车窗为研究对象，基于薄板理论，利用Hamilton原理和声学Rayleigh积分建立了弹性边界车窗的耦合FE-BE声振预测模型。研究了边界出平面平动和转动刚度及它们产生的边界阻尼对车窗声辐射的影响规律。研究结果表明：

（1）改变车窗边界支撑刚度的取值可模拟车窗在经典边界条件下的声振特性，本文得到的经典边界条件下的模态分析结果与ANSYS吻合很好；本文得到经典边界条件下的声辐射与无限大板的结果在质量和吻合控制区吻合很好，这说明本文建立的FE-BE模型对于研究高速列车车窗在弹性边界下的声振特性是准确有效的。

（2）边界平动刚度对高速列车车窗声辐射的影响较转动刚度的影响大。当边界平动刚度较小（约小于1×103N/m）时，车窗的声辐射与无限大板的结果相似；当边界平动刚度居中（1×103～1×106N/m）时，车窗的声辐射开始出现模态峰值，且随刚度急剧变化；当边界平动刚度较大（约大于1×106N/m）时，车窗的声辐射随刚度变化不明显，趋于稳定。

（3）提高边界阻尼有助于抑制高速列车车窗在低频模态峰值附近的辐射声功率，但作用有限；由复平动刚度产生的边界阻尼对车窗声辐射的影响较由复转动刚度产生的边界阻尼大。

[1]Jin XS. Key problems faced in high-speed train operation [J]. J Zhejiang Univ Sci A，2014（15）：936-45.

[2]张捷. 高速列车车内低噪设计方法及试验研究[D]. 成都：西南交通大学，2018.

[3]李明，韩铁礼，朱荟吉，等. 高速列车组合地板结构隔声性能分析[J]. 机械，2020，47（10）：60-65.

[4]张传英，张继业. 基于仿生形态的高速列车气动性能研究[J]. 机械，2019，46（4）：42-47.

[5]Baldanzini N，Pierini M，Scippa A. SEA modeling of an high speed train window [C]. International Conference on Noise and Vibration Engineering，Catholic University of Leuven Press，2002：765-773.

[6]Yang Li. Numerical optimization of sound insulation performance for the new type glass window based on genetic algorithm and its application in high-speed trains [J]. Journal of Vibroengineering，2016（18）：606-621.

[7]Zhang YM，Xiao XB，Thompson DJ. Sound transmission loss of windows on high speed trains [C]. 13th International Conference on Motion and Vibration Control，IOP Publishing Ltd.，2016：012141.

[8]张玉梅，王瑞乾，李晔，等. 高速列车车窗隔声量研究 [J]. 机械工程学报，2018，54（2）：212-221.

[9]Xin FX，Lu TJ，Chen CQ. Vibroacoustic behavior of clamp mounted double-panel partition with enclosure air cavity [J]. Journal of the Acoustical Society of America，2008，124（6）：3604-3612.

[10]Xin FX，Lu TJ，Chen CQ. Sound transmission through simply supported finite double-panel partitions with enclosed air cavity [J]. Journal of Vibration and Acoustics，2010，132（1）：011008.

[11]Xu ZX，Shi GT，Diao XG，et al. Research on control effect of window glass on inner sound environment of high-speed train [C]. 2019 IEEE International Conference on Mechanics and Automation，IEEE，2019：240-245.

[12]Hashemi SH，Khorshidi K，Taher HRD. Exact acoustical analysis of vibrating rectangular plates with two opposite edges simply supported via Mindlin plate theory [J]. Journal of sound and vibration，2009，322（4-5）：833-900.

[13]钟阳，李锐，田斌. 四边简支矩形板自由振动的哈密顿解析解[J]. 应用力学学报，2011，28（4）：323-327.

[14]Du JT，Liu ZG，Yang TJ，et al. Vibro-acoustic coupling of a rectangular cavity backed by a flexible panel with general boundary conditions [J]. Journal of the Acoustical Society of America，2009，（125）：2693.

[15]王久法. 矩形板及其耦合结构的振动建模方法研究[D]. 哈尔滨：哈尔滨工程大学，2014.

[16]Ou DY，Mak CM. Experimental validation of the sound transmission of rectangular baffled plates with general elastic boundary conditions [J]. The Journal of the Acoustical Society of America，2011，129（6）：EL274-EL279.

[17]Ou DY，Mak CM. The effects of elastic supports on the transient vibroacoustic response of a window caused by sonic booms [J]. The Journal of the Acoustical Society of America，2011（130）：783.

[18]Zhang J，Xiao XB，Sheng XZ，et al. SEA and contribution analysis for interior noise of a high speed train [J]. Applied Acoustics，2016（112）：158-170.

[19]Yao Dan，Zhang Jie，Wang Ruiqian，et al. Vibroacoustic damping optimisation of high-speed train floor panels in low- and mid-freqeuency range [J]. Applied Acoustics，2021（174）：107788.

[20]Sheng X, Zhong T, Li Y. Vibration and sound radiation of slab high-speed railway tracks subject to a moving harmonic load [J]. Journal of Sound and Vibration，2017（395）：160-186.

Research on Elastic Boundary Supports on Sound Radiation of High-speed Train Windows

ZHU Huiji1，QI Yuwen2，XU Jiaming2，DENG Tiesong1，JIN Xuesong1

( 1.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China;2.CRRC Changchun Railway Vehicles Co., Ltd., Changchun 130062, China )

In order to study the sound radiation (SR) of the high-speed train windows, a coupling finite element and boundary element (FE-BE) model of the window subject to elastic boundary supports is established based on the Hamilton principal and the Rayleigh integral. In the model, the elastic boundary supports are simulated as translation and rotation springs continuously distributed along the periphery of the window. The FE-BE model is verified by comparing the results with the modal analysis of a rectangular plate subject to classical boundary conditions and the SR of an infinite plate. Using the FE-BE model, the effect of boundary spring stiffness on the SR of the window is analyzed and the influence of the damping arising from the boundary springs is investigated. The results show that the stiffness of the translation springs has a more significant influence on the SR than that of the rotation springs; when the stiffness of the translation springs is less than 1×103N/m, the SR of the window is similar to that of an infinite plate; when the stiffness ranges from 1×103to 1×106N/m, several significant SR peaks caused by the modes of the window emerges and varies rapidly with the stiffness increasing; when the stiffness is even larger, the SR tends to be stable; increasing the boundary damping is helpful to suppress the SR near the peaks, while the impacts are limited; the damping arising from the translation springs has greater effect on the SR of the windows than that from the rotation springs.

high-speed train；window；elastic boundary；finite element method；boundary element method；sound radiation

U270.1+6

A

10.3969/j.issn.1006-0316.2021.10.005

1006-0316 (2021) 10-0030-08

2021-03-23

国家自然科学基金（U1934203）

朱荟吉（1995－），女，江苏无锡人，硕士研究生，主要研究方向为高速列车板件结构的振动噪声，Email：760551262@qq.com。*通讯作者：金学松（1956－），男，江苏扬州人，博士，教授，主要研究方向为轮轨关系和伤损、轨道交通振动噪声与控制，Email：xsjin@swjtu.edu.cn。