基于自适应模糊PID的液控稳频水流发电系统研究
陈勇洁,林晓焕,吕广雷,李峙毅,罗岩,钟世龙
基于自适应模糊PID的液控稳频水流发电系统研究
陈勇洁,林晓焕,吕广雷,李峙毅,罗岩,钟世龙
(西安工程大学 机电工程学院,陕西 西安 710048)
针对现有液控稳频自然水流发电装置控制系统响应时间长,控制精度不足,超调量大,达到稳态时间过长等不足,提出了一种基于自适应模糊PID的液控稳频水流发电系统,对变排量马达及其变排量机构进行数学建模,推得传递函数,通过MATLAB工具箱设计了模糊控制器,利用控制变量思想对控制系统进行仿真,对比传统PID和模糊PID的仿真结果得出结论:采用自适应模糊PID的液控稳频水流发电系统有更好的控制精度,超调量小,达到稳态时间更短、鲁棒性强等优势。
水流发电;液控稳频;模糊PID;MATLAB仿真
随着全球工业的不断发展,石油、煤炭等化石燃料能源消耗量巨大,自然环境也深受影响,包括水能、风能以及太阳能等在内的自然动力成为各国高度重视的焦点[1-2]。其中,自然水流能具有蕴藏储量大、功率密度大等特点,相对于传统的水力发电系统,自然水流发电系统对生态环境破坏较小[3]。因此,对自然水流发电装备技术的研究与工业性开发具有重大的现实意义和长远价值。
我国的自然水流能资源储蓄是相对较为丰富的,然而江河、海水这些自然水流的动能并未能被充分利用。我国的水电行业起步较晚,目前我国的水电技术与国际先进水平也仍有差距,主要技术难点在于:自然水流流速、流量不稳定,且一般无明显变化规律,水轮机捕获的能量也随之无规律变化,如何利用这样不稳定的动力源实现恒频高质量发电是一大技术难题[4]。而针对此问题采用较多的是变速恒频技术,该方案通过将频率不稳定的交流电转变为直流电,再转变为工频交流电,过程中会有大量的谐波产生,对发电质量产生较大影响。
液控稳频技术对解决此类自然水能、风能等不可控且无明显变化规律的动力源问题有突出优势。将水轮机从自然水流捕获到的不稳定机械能转化为液压能,再通过基于变排量马达和比例调速阀的复合调速方法,将液压能调节稳定,从而使得马达输出稳定的机械能给发电机,实现恒频高质量发电[5]。
然而,现存液控稳频水流发电装置控制系统采用传统PID控制,存在控制精度不足、超调量大、达到稳态时间过长等问题[6-8]。为此,本研究针对以上问题采用自适应模糊PID控制算法,经理论分析与建模仿真得出结论:算法改进使得液控稳频水流发电系统得到更好的控制精度,且超调量更小,达到稳态时间更短,鲁棒性更强[9-10],使得马达输出转速更快稳定在1500 r/min左右,能更好地实现发电机稳频发电。
1 液控稳频原理
液控稳频系统原理如图1所示,核心元件有水轮机、液压泵、电磁溢流阀、比例调速阀、变排量马达等[5,11]。

1、21.吸油滤油器;2.补油泵;3、20.电磁溢流阀;4、22.回油滤油器;5、13、17、18.压力表;6.单向阀;7.液压泵;8.电磁溢流阀;9.蓄能器;10.高压滤油器;11.比例调速阀;12、16.压力传感器;14.变量马达;15.发电机;19.变量机构泵;23.液位计;24.油温计;25.水轮机。
水轮机从自然水流捕获能量,从而驱动主泵7,液压系统实现水流能—机械能—液压能的能量转换,此时液压能依然是非稳定动力。在主油路中,马达变排量机构首先对马达排量进行调节(粗调),再经比例调速阀11进行旁路调节(微调)使得马达输出转速波动范围更小。马达稳定输出转速,向发电机提供稳定动力,使得发电机实现稳频发电。溢流阀的作用是主要是控制进入变量马达的油液压力。低速大流量泵7因其本身特性,在工作过程中会产生压力脉动和流量脉动,所以在主回路中设置蓄能器9以减小脉动,同时,蓄能器的加入也可以有效提升系统的响应速度和稳定性。
闭式液压回路以其高效、布局紧凑、高功率密度以及油箱体积更小的特点在行走机械液压系统中得到广泛应用。在本文液控稳频系统中,由于系统所需流量较大,因此,与常规液压系统不同,本文液压系统中将马达14出油口直接连接到主泵7的入口,形成局部闭式液压回路,闭式液压回路的设计可大大减小主泵从油箱中抽取的油量。与此同时,设置补油泵2对液压泵和液压马达以及各种阀可能存在的泄漏进行油量补充,同时也在很大程度上弥补了液压泵自吸能力较差的问题。设置变排量机构泵19为马达变排量机构(阀控缸)提供动力源。
2 变排量马达数学建模
变排量马达的变排量机构通过阀控缸(四通阀控制液压缸)的方法来实现,利用液压缸将特定控制量的位移传送到马达缸体上,以此来控制变量马达的排量。因此,在对变排量马达进行数学建模时,除了对变排量马达本身进行数学建模以外,还要对变排量机构进行数学建模[5,11]。
2.1 马达变排量机构的数学模型
根据马达变排量机构的特性,且由于马达的斜盘为一个大惯量部件,且在此将马达的变排量控制系统简化为一个一阶系统。控制电压与马达排量的关系可表达为:

2.2 变量马达转速控制的数学模型
考虑油液压缩性和变量马达油液泄漏,变量马达的流量连续方程可取为:
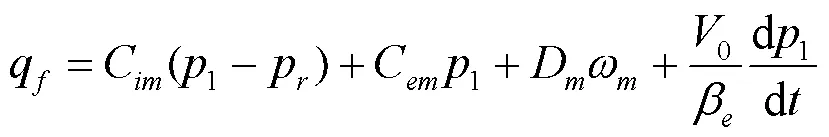
经拉氏变换后,得:

变量马达的负载力矩平衡方程为:

对式(4)进行拉氏变换,得:

式中:J为变量马达和负载(折算到变量马达轴上)的总惯量,kg/m2;B为黏性阻尼系数;T为作用在变量马达轴上的任意外负载力矩,N/m。
由式(3)和式(5)可得变量马达传递函数为:


式中:ω为变量马达的固有频率,Hz;ζ为变量马达的阻尼比。
变量马达转速对其排量的传递函数为:

变量马达转速对输入流量的传递函数为:

变量马达转速对外负载的传递函数为:

观察以上传递函数不难得出结论——三个传递函数均为振荡环节,可以利用霍尔维茨判据式来判断其稳定性。马达转速对其排量、输入流量以及外负载的三个传递函数均为二阶系统特征方程,且其中各项系数均为正值,因此从理论分析来看其工作总是稳定的。
3 自适应模糊PID控制系统仿真
自然水流发电的恒速控制系统主要实现对变量马达和阀组的控制,水流速度是在不断变化的,所以定量泵的输出流速也是变化的,通过对变量马达与阀组的调速系统的控制,实现对变量马达转速的恒定输出[11-12]。考虑到控制系统的精度,到达稳态的时间,以及鲁棒性等要求,控制系统采用自适应模糊PID算法,控制原理框图如图2所示。

图2 控制系统结构框图
当泵的输出转速随自然水流变化时,模糊控制器通过偏差和偏差变化率e以及给定的模糊规则,向PID控制器输出PID控制参数,PID控制器调节变量马达变排量机构对马达转速进行粗调,使得马达转速基本稳定后,再由比例调速阀进行微调,通过变排量马达和比例调速阀复合调速的方法,使得马达输出转速恒定在1500 r/min[13-14]。
3.1 模糊控制其设计
为了模拟自然水流的不稳定性,设定自然水流流速在5.5~7.5 m/s之间变换,对应取泵的输出转速为20~30 r/min,即在仿真过程中将液压泵设为20~30 r/min的渐变信号[15]。即的论域为[20, 30],e的论域设为[-1, 1],将论域划分为7个子集:{NB, NM, NS, ZO, PS, PM, PB},隶属度函数均采用三角形函数,采用重心法解模糊[16-17]。
基于模糊算法的多种应用场景以及专家总结的经验,取模糊规则如表1所示。

表1 模糊规则表
3.2 PID控制器设计
利用上述的模糊控制策略,可根据控制过程中的实时状态,对PID参数进行调整,调整规则如下:

式中:K、K、K分别为PID控制器的初始值[18]。
整定后的PID参数通过下式得出最后的信号控制量输出为:

3.3 基于MATLAB的控制仿真对比
如图3所示,在Simulink中调用已经设计好的模糊控制器,对模糊PID控制系统进行建模,并设置传统PID控制系统作为对比。在工程实践中,PID参数无准确固定的确定方法,在本文中,PID参数根据临界比例法、反应曲线法,再综合工程实践经验调节设定[19-21]。
经过多次仿真模拟,最终确定K=0.2、K=20、K=1.6为最优初始值。

图3 Simulink仿真框图
仿真结果如图4所示,通过对比可以得出结论:在本研究中自适应模糊PID控制系统相对于传统PID而言,超调量更小,达到稳态的时间也更短,符合算法改进预期。
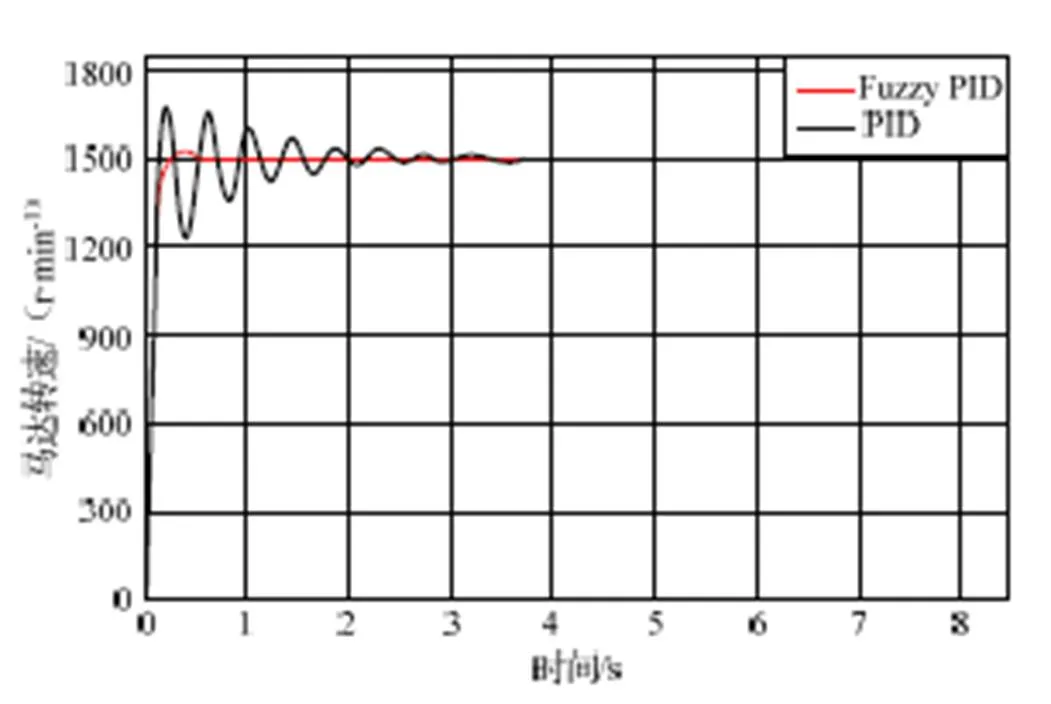
图4 模糊PID与传统PID仿真结果对比
4 结束语
在实际工程应用中,对控制系统的稳定性与时效性有很高的要求。在液控稳频自然水流发电系统中,由于源动力不稳定且无明显变化规律,相比传统PID控制而言,自适应模糊PID控制系统能更快地到达稳态,超调量小,且表现出更好的适应性、鲁棒性,使得液控稳频自然水流发电系统在复杂应用环境下表现出更好的适应性。
[1]张琰,高强,闫宏伟,等. 微水头水流能发电装置导流罩水动力性能研究[J]. 人民长江,2020,51(10):187-191.
[2]张刚,乔伟,韩迎鸽,等. 江河水流能发电影响因素分析及试验研究[J]. 华电技术,2020,42(2):76-80.
[3]孟维文. 小型水流能发电装置设计与仿真[D]. 武汉:武汉理工大学,2012.
[4]王鹏飞. 哈密顿理论体系下水力发电系统稳定性研究[D]. 咸阳:西北农林科技大学,2019.
[5]杨振宇,马训鸣,崔建鑫. 基于变量泵控定量马达的风力发电系统建模仿真与试验研究[J]. 节能技术,2018,36(2):120-124.
[6]张婧,马训鸣. 基于模糊PID控制的六自由度液压系统[J]. 西安工程大学学报,2015,29(6):702-707.
[7]王延年,郭卫松,陈苗苗. 基于DSP的高精度智能电液伺服控制器的设计[J]. 西安工程大学学报,2013,27(2):198-202.
[8]Gao Qiang,Lu Zhixiong,Xue Jinlin,et al. Fuzzy-PID controller with variable universe for tillage depth control on tractor-implement[J]. Journal of Computational Methods in Sciences and Engineering,2021,21(1):19-29.
[9]Carpio Marco,Saltaren Roque,Viola Julio,et al. Proposal of a Decoupled Structure of Fuzzy-PID Controllers Applied to the Position Control in a Planar CDPR[J]. Electronics,2021,10(6):745-745.
[10]邹权,钱林方,蒋清山. 永磁同步电机伺服系统的自适应模糊滑模控制[J]. 控制理论与应用,2015,32(6):817-822.
[11]俞齐鑫,马训鸣. 液控稳频风力发电系统建模仿真与试验研究[J]. 液压与气动,2014(10):70-73.
[12]毛尾,纪朱珂,韦海利,等. 电液比例伺服系统模糊PID复合控制应用研究[J]. 液压与气动,2019(1):95-99.
[13]杨春,郭健,张磊,等. 采用卡方检验的模糊自适应无迹卡尔曼滤波组合导航算法[J]. 控制与决策,2018,33(1):81-87.
[14]彭思齐,宋彦彦. 基于自适应模糊滑模观测器的永磁同步电机无传感器矢量控制[J]. 控制与决策,2018,33(4):644-648.
[15]郭娜,胡静涛. 基于Smith-模糊PID控制的变量喷药系统设计及试验[J]. 农业工程学报,2014,30(8):56-64.
[16]徐娟,陈时桢,何烊剑,等. 基于模糊PID的平衡头自适应控制策略研究[J]. 电子测量与仪器学报,2016,30(6):895-902.
[17]陈斌,裴忠才,唐志勇. 液压四足机器人的自适应模糊PID控制[J]. 哈尔滨工业大学学报,2016,48(9):140-144.
[18]Mohanty Debidasi,Panda Sidhartha. A modified moth flame optimisation technique tuned adaptive fuzzy logic PID controller for frequency regulation of an autonomous power system[J]. International Journal of Sustainable Energy,2021,40(1):41-68.
[19]Chenzhong Pu, Xiangguo Sun. Research on Temperature Control of Box-type Resistance Furnace Based on Fuzzy PID[J]. International Core Journal of Engineering,2021,7(1):438-444.
[20]葛媛媛,张宏基. 基于自适应模糊滑模控制的机器人轨迹跟踪算法[J]. 电子测量与仪器学报,2017,31(5):746-755.
[21]熊雄,王江波,杨仁刚,等. 微电网中混合储能模糊自适应控制策略[J]. 电网技术,2015,39(3):677-681.
Hydraulic-Controlled Frequency Stabilized Water Flow Power Generation System Based on Self Adaptive Fuzzy-PID
CHEN Yongjie,LIN Xiaohuan,LYU Guanglei,LI Zhiyi,LUO Yan,ZHONG Shilong
( School of Mechanical and Electrical Engineering, Xi'an Polytechnic University, Xi'an 710048, China)
Aiming at solving the problems of long response time, insufficient control accuracy, large overshoot, and long time to reach the steady state of the existing hydraulic-controlled frequency stabilized natural water flow power generation system, a new power generation system based on adaptive Fuzzy-PID is proposed. Mathematical model of variable displacement motor and its variable displacement mechanism is established and the transfer function is obtained. A fuzzy controller is designed through the MATLAB toolbox and the control system is simulated by using the idea of control variable. Comparing the simulation results of traditional PID and Fuzzy-PID,we conclude that the hydraulic-controlled frequency stabilized water flow power generation system using adaptive Fuzzy-PID has the advantages of better control accuracy, small overshoot, shorter time to reach steady state, and strong robustness.
water flow power generation;hydraulic-controlled frequency stabilized;Fuzzy-PID;MATLAB simulation
TH137
A
10.3969/j.issn.1006-0316.2021.10.003
1006-0316 (2021) 10-0016-06
2021-05-11
西安市科技局基金(GXYD7.9)
陈勇洁(1994-),男,陕西清涧人,硕士研究生,主要研究方向为机电控制、液压,E-mail:2873573272@qq.com。*通讯作者:林晓焕(1964-),女,陕西西安人,教授,主要研究方向为数据通信与计算机控制,E-mail:li826850999@126.com。

