基于贝叶斯Logit模型的死亡事故发生概率分析

魏福禄，蔡正干，闫仲荣，李平凡，郭永青*，陈龙

(1.山东理工大学 交通与车辆工程学院， 山东 淄博 255000；2.东南大学 交通学院， 江苏 南京 211102；3.淄博市公安局交通警察支队 事故处理科， 山东 淄博 255000；4.公安部交通管理科学研究所， 江苏 无锡 214000)

0 引言

机动车使得交通出行更便捷，提高了人们的生活品质，可是随着汽车保有量的增长，交通事故尤其是死亡事故数量也随之增加，对道路交通安全产生恶劣影响。交通事故发生概率是交通安全的重要评价指标，事故发生概率尤其是死亡事故发生概率的上升，是对交通安全问题最强烈的警示。大量研究表明，交通事故的发生及其严重程度与事故形态、事故时间、天气条件以及能见度等多种因素存在稳定的内在关联[1-3]，揭示交通事故伤亡情况的主要影响因素，对减少人员伤亡和经济损失，提升交通安全水平至关重要。

随着人们安全意识的提高，对交通事故影响因素的研究得到了业界的持续关注，国内外学者基于对历史交通事故数据的分析和处理，建立交通事故模型，剖析影响交通安全的因素。交通事故的出现具有一定的随机性，受诸多因素影响，且一定时间内的交通事故数量是非负整数，具有离散的性质，可通过建模来分析交通事故与其影响因素之间的关系，至今已形成较为全面的理论体系，在发达国家得到了广泛的运用[4-5]。由于在事故影响因素的研究过程中涉及数据类型的差异，使得理论研究的侧重点也存在差异，例如XU等[6-7]强调降雨对交通事故的影响，PANG等[8]则关注低能见度条件下交通事故的特点。从不同的角度，通过历史事故数据挖掘和建模，剖析交通事故发生规律，指导交通安全设计和预防。

针对天气因素对事故风险的影响，学者们的研究结果不尽相同。ZHAI等[9]利用香港的事故数据研究了天气状况与人车事故严重程度的关系，发现天气条件对事故风险及其严重程度的影响显著，恶劣天气会增加驾驶人危险驾驶和行人违规横穿马路的行为，导致事故风险和严重程度高于晴朗天气。THEOFILATOS[10]基于雅典公路事故数据研究了天气和交通量等因素对交通事故的影响，发现交通量对事故发生概率有显著影响，但考虑雅典天气的特殊性，得到天气因素对雅典的事故风险没有显著影响的结论。SHAHEED等[11]研究了美国爱荷华州冬季发生的交通事故，分析不同天气、能见度状况以及事故类型等因素对乘客受伤严重程度的影响，发现在能见度和天气状况均良好的情况下，由于机动车行驶速度较快，发生交通事故时容易对乘客造成严重伤害，并且当机动车与相向行驶的车辆或者固定物发生碰撞时，更易发生严重交通事故。AHMED等[12]利用美国怀俄明州的交通事故数据研究了天气、事故类型对交通事故的影响，发现冰雪天气的事故发生概率最高，并且碰撞严重程度高于晴朗天气。

不同时间区段对事故发生概率的影响区别显著。NORROS等[13]基于赫尔辛基环城公路的事故数据研究了时间区段、能见度等因素对事故风险的影响，模型结果显示一天中不同时间段的事故风险是显著不同的， 下午15:00-17:00时的事故风险高于白天其他时段，上午9:00-10:00时的事故风险是最低的，并且夜晚发生交通事故的风险稍高于白天，同时不同能见度的事故风险也是不同的，能见度降低会增加事故风险。赵跃峰等[14]利用发生在公路的交通事故研究了不同时段的事故风险，结果发现夜间出现轻伤、重伤或死亡事故的概率均高于白天。本质上，事故本身带有很大的随机性，只是外界环境影响驾驶人、行人的行为以及汽车的性能，使得这种随机性的概率变大。

中国与欧美的交通运行特性之间存在着差异，其交通事故研究成果只可借鉴，却很难直接应用在我国交通安全管理中，同时利用不同类型数据建立的事故分析模型，其时空可迁移性亦有待验证。因此，本文以淄博市道路交通事故数据为基础，利用贝叶斯Logit回归模型研究不同因素对我国交通事故中出现人员死亡概率的影响，对明确事故预防重点，减少人员伤亡和经济损失，提升交通安全水平至关重要。

1 数据描述

课题组对淄博市2013—2018年的交通事故进行了系统梳理，遴选出有人员受伤或死亡的交通事故作为样本数据库，其中每起事故数据都记录了人员伤亡情况、事故地点、时间、日期、事故类型、天气状况、车辆信息以及事故发生时的大气能见度。考虑到在常规作业中，样本数据中的天气和能见度信息是警察在处理现场时凭经验估计的，并且由于从事故发生到警察到达现场存在着时间间隔，天气和大气能见度有可能发生变化等原因，我们调取了布设在各区县的20个气象监测仪的数据，以准确获取天气和能见度等信息，气象监测仪布设位置及事故研判区域如图1所示。根据事故数据中提供的事故地点和时间，利用ArcGIS在地图上进行定位，并调取距离最近的气象仪在该时间点的监测数据，标定该起事故的天气和能见度参数，若数据丢失，则以相近气象仪的监测数据为参考。

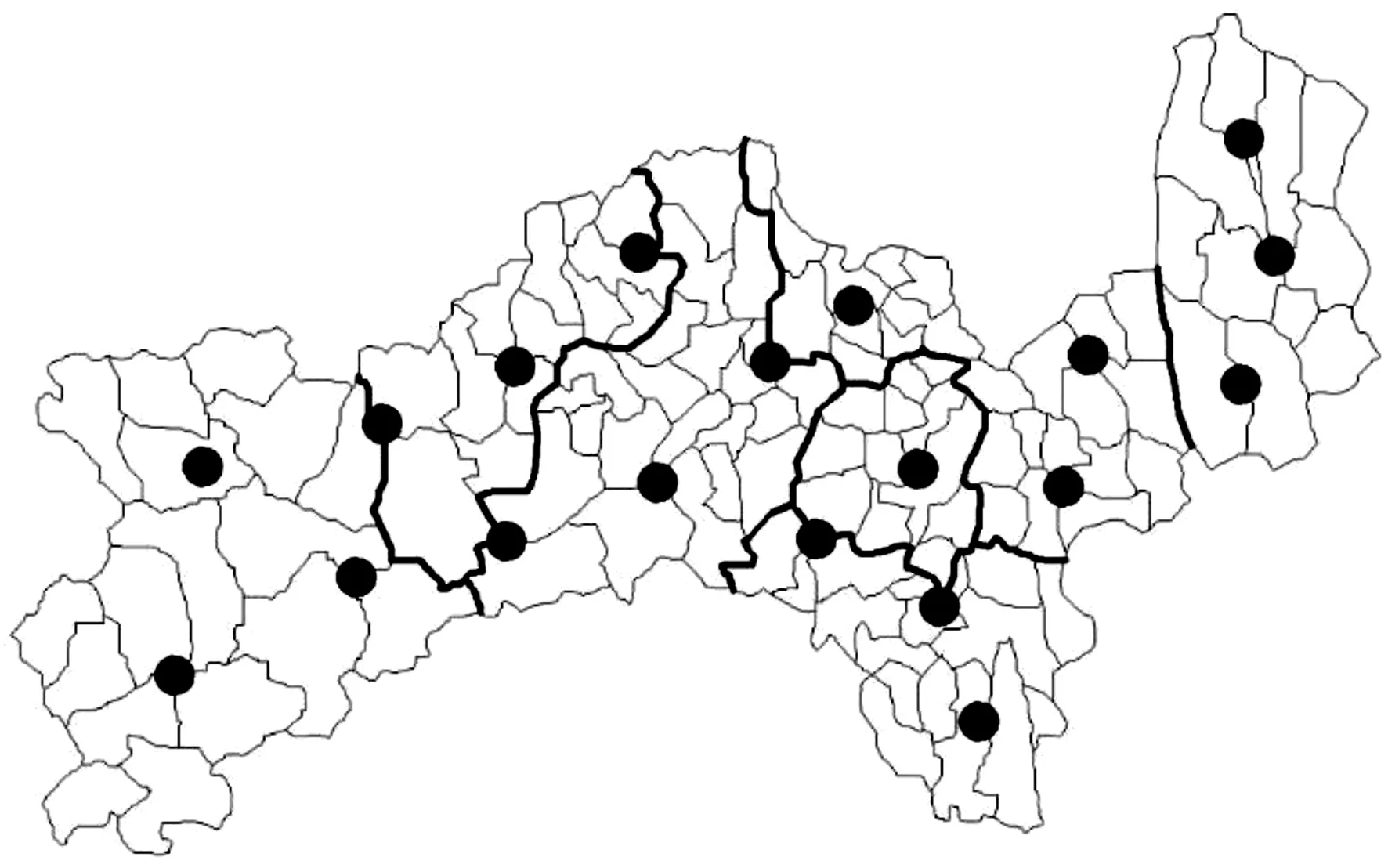
图1 气象监测仪布设位置及事故研判区域

为便于事故研判与建模，将所涉及因素进行了分类变量转化，根据数据间的内在逻辑关系对其进行编码，且研究的变量均为无序分类变量。若研究的因素为二值变量，则编码为0与1。若包含多个变量，无论与事故有无直接关系，各因素的变量编码均以0开头，按数字顺序对不同变量作编码，将编码为0的变量，在建模过程中作为该因素的基准变量。模型中考虑的因素有：事故发生地区、时间、周、事故类型、天气、季节以及能见度，对交通事故影响因素的分类编码和数据描述见表1。

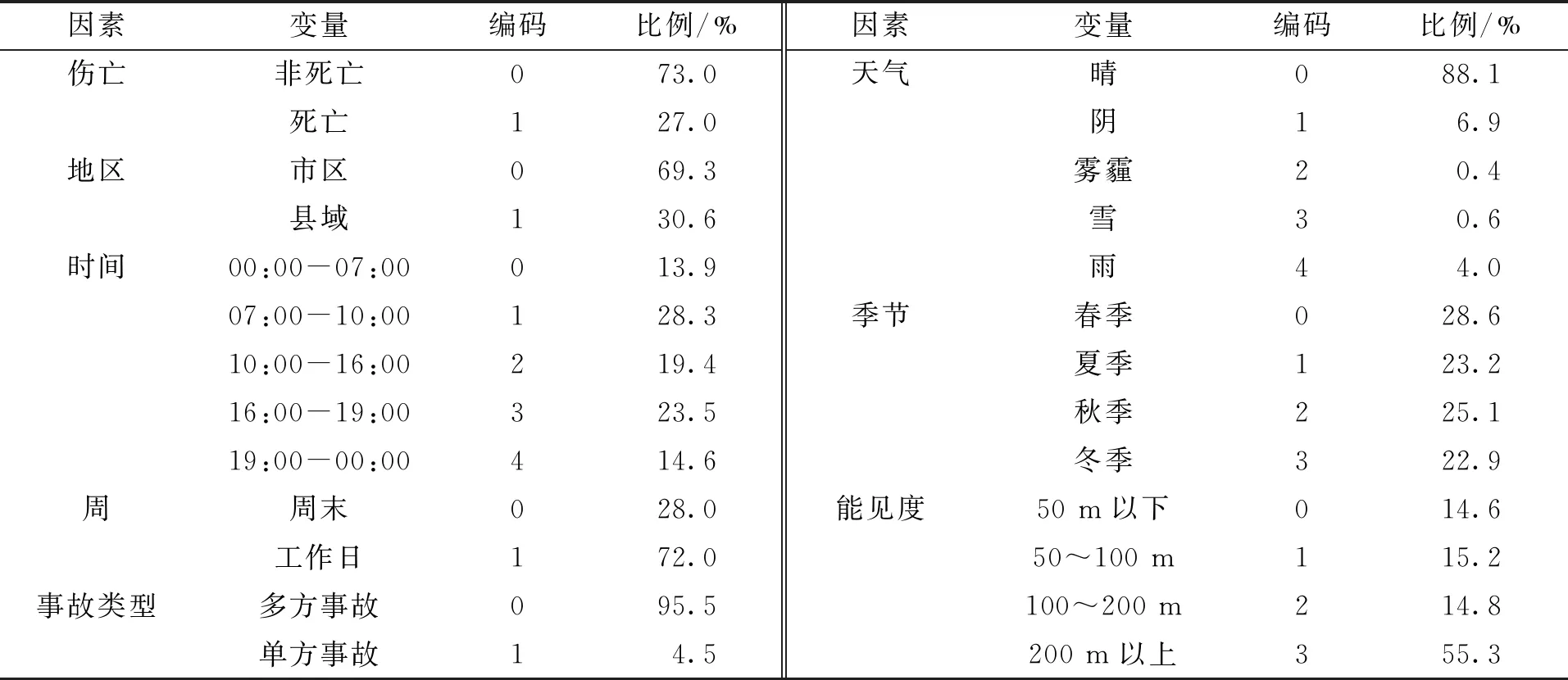
表1 交通事故影响因素的分类编码和数据描述

根据每起交通事故的伤亡情况，以受伤最重者为参照对交通事故进行二值分类，即死亡交通事故与非死亡交通事故，其中死亡事故占样本量的27.0%。在所有的样本中，单方事故占样本量的4.5%，其余为多方事故，可见发生受伤或死亡的多方事故的概率远高于单方事故。其次，市区事故占样本的69.3%，数量多于县域。这是由于市区的汽车保有量较高，且道路里程和交通量较大导致的。对于不同时间区段，早高峰(7:00-10:00)发生事故最多，占样本的28.3%，其次是晚高峰(16:00-19:00)，占比为23.5%，凌晨时段(00:00-07:00)事故量最低，占总样本的13.9%

在不同天气条件下，88.1%的交通事故发生在晴天，远超其他天气条件下的事故数。之前的研究发现，恶劣天气会导致路况不佳、能见度变差，影响车辆的操纵和驾驶员自身的状况，使得事故率较高。但根据气象仪记录的数据，晴天在一年中所占比例超过80.0%。所以，晴天的事故发生概率虽然较低，但由于持续时间长，从而导致事故总数较大。在恶劣天气条件下，发生事故最多的是降雨天气，占样本量的4.0%。从事故发生时的能见度来看，能见度在200 m以上的事故量最大，占总事故量的55.3%，能见度在200 m以下不同区段的事故量差别并不明显。

2 贝叶斯Logit回归模型

将事故发生的地区、时间、类型、天气、季节、能见度等因素作为模型的无序分类解释变量，以事故严重程度为二值响应变量(死亡事故赋值为1；非死亡事故赋值为0)进行建模分析，探究不同因素对死亡事故发生概率的影响。

2.1 贝叶斯Logit回归模型的构建

经典Logistic回归实质是一种广义线性模型，将模型参数视为固定的未知常量，用数据来估计参数的最佳值。在贝叶斯方法中，参数被视为随机变量，用数据拟合参数，以评估其分布特性。考虑到贝叶斯Logit模型具有逻辑方程的形式和贝叶斯推理的优点，在分类变量处理方面有着优良的性能和表现，故采用贝叶斯Logit回归方法进行建模。

在研究中，假设模型未知参数的先验信息服从正态分布，利用极大似然法对模型初始参数进行估计。另外，贝叶斯方法和经典统计学是不同的，贝叶斯利用先验信息，并将先验信息量化形成先验分布，加入到统计推断中，然后根据总体信息、样本信息和先验分布推导参数的后验分布，构造可信区间，对参数进行概率解释，并对参数的后验分布给出精确的度量，从而克服极大似然法因忽略参数估计的不确定性而高估精度的问题，有效避免样本数量有限且变量较多时模型的过拟合问题。贝叶斯模型表达式，如公式(1)：

(1)

式中，Yi为二分因变量；P(Yi)为Yi的先验分布；P(Yi|Xk)为参数Yi在样本Xk下的后验分布；P(Xk|Yi)是似然函数；P(Xk)为Xk的边缘密度函数。

贝叶斯Logit模型构建了二分类因变量Y与天气、时间、季节和能见度等自变量X间关系的拟合模型。当第i起事故有人员死亡时，Yi=1；否则，Yi=0。其概率分别为pi和(1-pi)，pi的取值范围是0至1，Logit回归方程见公式(2)：

(2)

式中，β0是模型常数项；Yi是二分类因变量；Xn,i为自变量；βn是自变量相关的未知参数。

模型将自变量Xn,i与因变量Yi通过函数联系起来，设有n个因素与Y有关，记作X=(x1,i,x2,i,…,xn,i)，则在n个因素下，Yi=1时概率P的计算公式推导，如公式(3)所示：

(3)

利用贝叶斯Logit回归模型对事故数据进行建模就是用数学的表达方法对交通事故发生死亡的概率及其影响因素进行分析和描述。如前文所述，关于事故伤亡情况的判断，以伤势最严重者为准，若事故中有人死亡，即认为该起事故是死亡事故，并编码为1，否则定性为非死亡事故，编码为0。

2.2 贝叶斯Logit回归模型的构建

为实现模型对事故数据更好的拟合，将其参数视为随机变量，运用贝叶斯方法对其进行估计，进而分析不同因素对事故严重程度的影响。由于正态先验下参数的后验分布形式复杂，计算高维积分求得解析解较为困难，因此，运用STATA调用蒙特卡洛马尔科夫链(monte carlo markov chains, MCMC)算法，利用吉布斯采样(Gibbs)得到样本的近似后验分布，并进行12 500次迭代。利用Raftery-Lewis诊断[15]监测马氏链的长度，模型经过约2 500次迭代后达到收敛，则马氏链的前2 500次迭代作为模型预迭代而舍弃，确保MCMC算法可以对参数后验分布作合理近似。得到的贝叶斯Logit模型参数标定见表2。

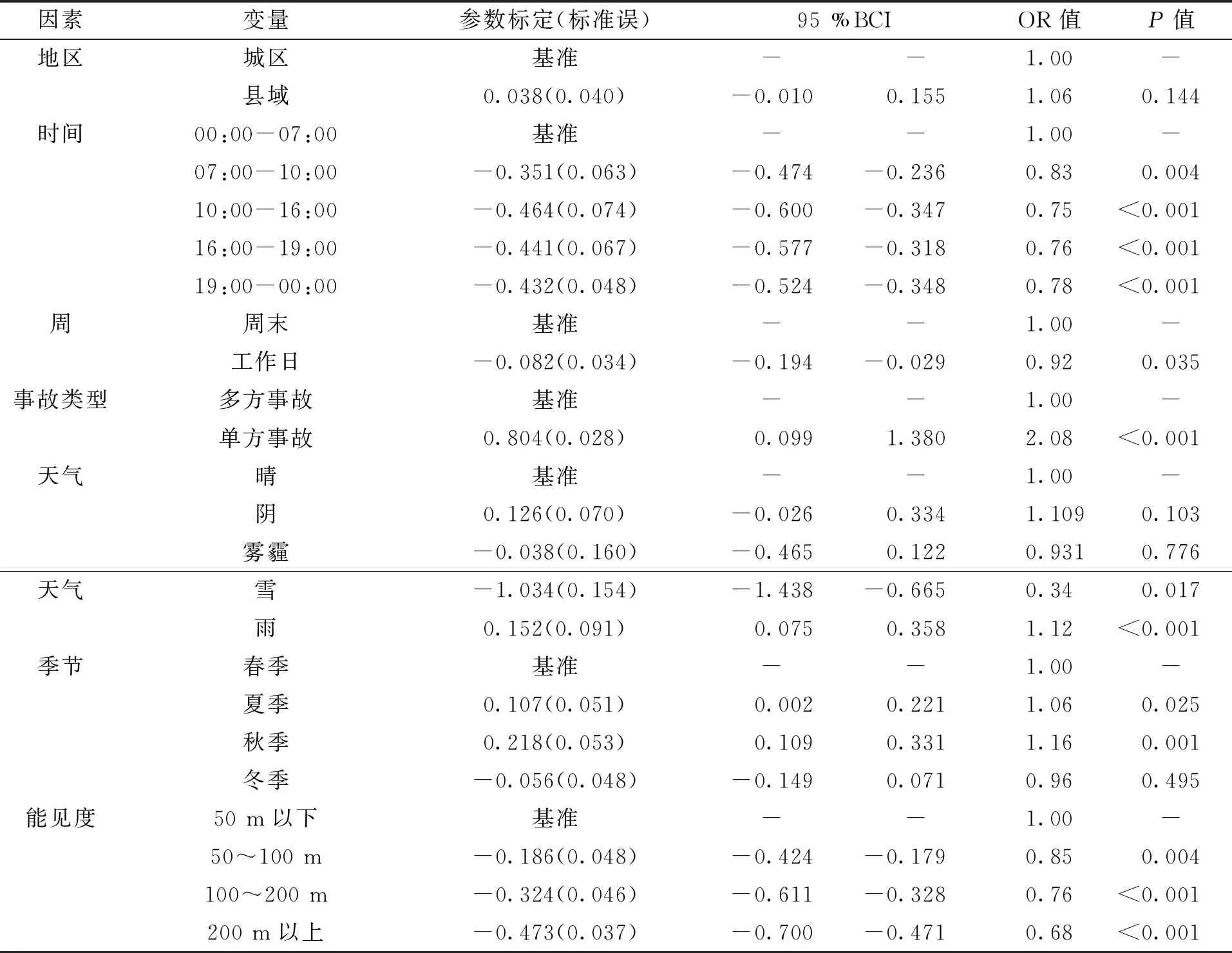
表2 贝叶斯Logit模型参数标定

模型利用OR值评价同一因素下不同变量对死亡事故发生概率的影响，OR值为1表示该变量作为基准变量，其他变量对输出结果的影响程度，更大(OR>1)或更小(OR<1)[16]，OR值计算模型的推导如下：

对Logit回归方程两边同时取底数e，得到公式(4)：

(4)

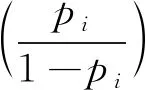
(5)

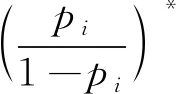
3 模型检验与讨论

3.1 模型拟合优度检验

为检验贝叶斯Logit模型对样本数据拟合的优劣程度，需对所构建的贝叶斯Logit模型进行检验。常用的贝叶斯模型的检验方法有两种：偏差信息准则(deviance information criterion, DIC)和接收者操作特性曲线(receiver operating characteristie, ROC)。其中，DIC适用于多个贝叶斯模型进行比较，不适于本次研究。ROC曲线可利用图像直观的表示模型敏感度和特异性之间的关系[17]，从而确定模型拟合优劣，所以选用ROC曲线对模型进行检验。ROC曲线与X轴、(1，0)和(1，1)所组成图形的面积用SAUC(area under curve, AUC)值表示，取值范围是0至1。AUC可以直观的评价分类器的好坏，值越大越好。当SAUC值越接近1时，表示模型拟合准确性越高，但可能永远不会等于0或1，因为模型准确率为100%或者为0的可能性极小。

贝叶斯Logit模型的ROC分析曲线如图2所示，图2中横轴表示负正类率(false positive rate，FPR)，亦称为1-特异度(1-specificity)，代表分类器预测的正类中实际负实例占所有负实例的比例，计算公式为FPR=FP/(FP+TN)；纵轴表示真正类率(true positive rate，TPR)，亦称为敏感度，代表分类器预测的正类中实际正实例占所有正实例的比例，计算公式为TPR=TP/(TP+FN)。需要说明的是，针对一个二分类问题，将实例分成正类或者负类，但是在实际分类时，会出现如下4种情况：①若一个实例是正类并且被预测为正类，即为真正类(true positive，TP)；②若一个实例是正类，但是被预测成为负类，即为假负类(false negative，FN)；③若一个实例是负类，但是被预测成为正类，即为假正类(false positive，FP)；④若一个实例是负类并且被预测成为负类，即为真负类(true negative，TN)。

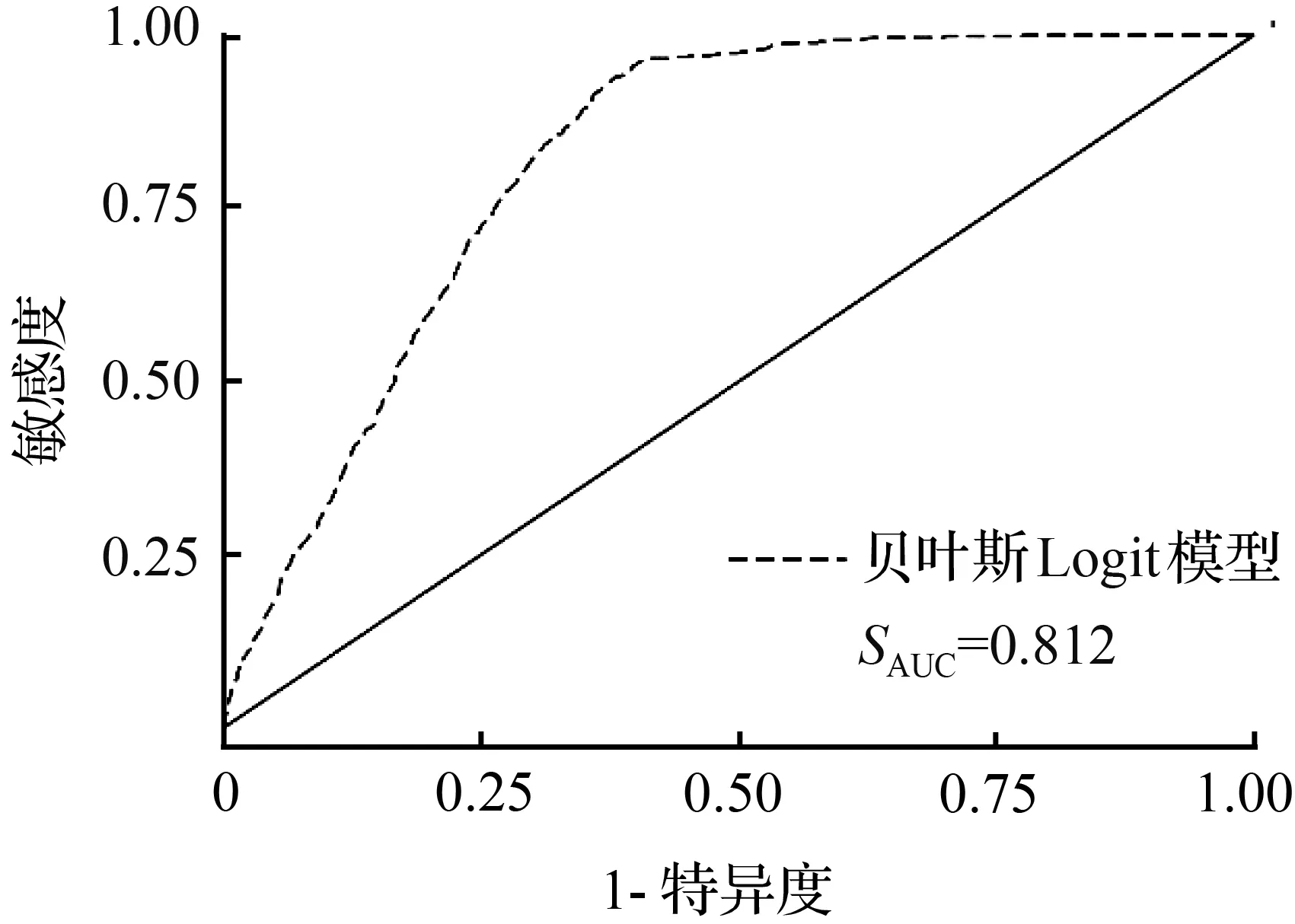
图2 贝叶斯Logit模型的ROC分析

ROC曲线涵义是，假设采用某种分类器，其给出针对每个实例为正类的概率，通过设定一个阈值如0.7，概率大于0.7的为正类，小于0.7的为负类，对应的就可以算出一组坐标点(FRT，TPR)。随着阈值的减少，越来越多的实例被划分为正类，但这些正类中所包含的真正的负实例也会越来越多，即TPR和FPR会同时增大。贝叶斯Logit模型的ROC分析如图2所示，根据贝叶斯Logit模型预测结果，在不同阈值下死亡事故发生概率的ROC分析曲线，其SAUC值为0.812接近于1，说明所建立的贝叶斯Logit模型拟合优度良好。

3.2 死亡事故发生概率的影响因素分析

为了分析不同因素对死亡事故发生概率的影响程度，利用基于贝叶斯推理的Logit回归模型对样本数据进行分析和建模，得到模型系数、标准误差、95%BCI、OR值以及P值。由表2可见，不同时间区段、是否为工作日、事故类型、天气、季节以及能见度等因素与发生严重交通事故显著相关，模型中的其他因素无统计学显著性。城区和县域作为两种不同类型的地区，城区的汽车保有量、公路里程、公路设施等都要明显优于县域，车流量也高于县域。模型中死亡事故发生在县域的P值为0.144(>0.05)相对于城区并不显著，说明县域与城区发生死亡交通事故的概率并无明显区别。

将一天24 h分为5个时间段：从事故数量看，早高峰(7:00-10:00)发生事故最多，其次是晚高峰(16:00-19:00)，早高峰和晚高峰交通量较大，事故总量较多。从模型死亡概率来看，凌晨时段(0:00-7:00)作为基准变量，其OR值最高，说明凌晨时段发生死亡事故的概率最高。凌晨时段时驾驶员的状态不佳，易疲劳驾驶，加上凌晨时段的交通管控较弱，驾驶员容易违章行驶，在发生严重事故时，更易导致死亡。在其他条件不变的情况下，早高峰(7:00-10:00)发生死亡事故的概率是凌晨时段的0.83倍，仅次于凌晨时段。在其他条件不变的情况下，中午时段(10:00-16:00)发生死亡交通事故的概率是凌晨的0.76倍，这一时段发生死亡交通事故的概率是最低的。

对单方事故和多方事故等不同事故类型而言，在其他条件不变的情况下，单方事故致死的概率是多方事故的2.08倍，这与数据库组成直接相关，因为交警6合1平台事故数据主要包含受伤和死亡事故，对于轻微剐蹭固定物或轻微托底的单方事故，在无人员伤亡且财产损失很低的情况下，当事人通常不会报案，该类小事故便不会被录入数据库。这也说明，当发生严重事故时，单方事故相对多方事故而言更易致死。

对不同的天气变量，晴天和阴天发生的事故最多，其次是雨天。从建模结果来看，在其他条件不变的情况下，雨天发生死亡事故的概率是晴朗天气的1.13倍，居于不同天气下死亡事故发生概率之最高；雪天发生死亡事故的概率是晴朗天气的0.34倍，发生严重交通事故的风险最低。这是由于降雨使路面湿滑，驾驶员视线变差，影响驾驶状态和车辆性能，尤其是一些激进型驾驶人，往往因大意而高估自身对车辆的控制水平，驾驶车速较快，更易导致死亡事故。但降雪会降低轮胎附着系数，出现车轮打滑现象，驾驶员在行驶中危险感更强，驾车时会很小心，死亡风险也随之下降。

在其他条件不变的情况下，不同季节对死亡事故发生概率的影响表明，秋季发生严重交通事故的概率最高，是春季的1.17倍，这可能是因为秋季的天气条件和能见度均较好，驾驶人行车速度较快导致的。对不同能见度而言，能见度在200 m以上时事故量最高，其余的能见度区间事故量相差并不明显。从建模结果来看，随着能见度的升高，发生死亡交通事故的概率依次降低，即能见度大小和死亡事故发生概率的关系呈现出反比，能见度低时，更易发生死亡事故。

4 结语

① 考虑地区、时间和天气等7种因素对死亡交通事故发生概率的影响，发现城区和县域的事故量虽差异较大，但县域死亡事故发生概率相较城区并无统计学显著性。县域交通量通常低于城区，交通事故死亡概率却不低于城区，有必要加强县域的交通安全警示和管理。

② 凌晨时段事故量最低，但发生交通事故时致死概率最高，有必要提高该时段驾车的安全警惕性；单方事故的数量远低于多方事故，但死亡交通事故发生概率高于多方事故，说明在发生严重的交通事故时，单方事故更易致死。

③ 在恶劣天气下，雨天事故量和死亡概率均高于其他天气，为降低恶劣天气条件下的死亡事故发生风险，交通管理部门要加强监管力度，尤其是雨天的监管力度，同时驾驶人也要提高警惕性，避免发生事故。

④ 对于不同能见度，死亡交通事故发生概率随着能见度的升高而降低，在能见度大于200 m时，事故量最高，但发生交通事故时出现人员死亡的概率最低。