基于情感强度的自动驾驶车辆决策机制探究

张俊友，任文浩，李思贤

(1.山东科技大学 交通学院， 山东 青岛 266590；2.北京交通大学 交通运输学院， 北京 100044)

0 引言

近年来，自动驾驶车辆成为交通领域研究的热点，它能够实时感知外界环境，通过智能化决策来降低交通事故的发生[1-2]。针对今后一个时期传统人工驾驶车辆与自动驾驶车辆混行的状态，为使车辆安全高效行驶，自动驾驶车辆的决策机制需要与人类保持一致。在危险工况下，人类的驾驶行为受到道德和法律的约束，会生成恐惧等情感[3]，本文尝试把情感因素融入到自动驾驶决策模型，使自动驾驶车辆具备类人思维，进行趋利避害。

情感信息的来源主要是语音信号、面部表情、运动姿态、生理信号等，其中生理信号通常是由情感的变化而触发人体内部器官产生的一系列生物电学特征变化的信号[4- 6]，很难因人的主观意念而改变，故基于生理信号的情感识别具有客观真实性。国内外学者通过多年深入研究，证明生理信号可用来测量情感，PICARD等[7]采集肌电信号、皮肤电导信号等多种生理信号，利用K近邻(k-nearest neighbor, KNN)分类算法识别恐惧等情感；KIM等[8]将情感的生理识别从单个向多个进行扩展，研发了一种情绪识别系统；MEHRABIAN等[9]提出PAD三维情感模型来描述人类不同的情感状态。

在自动驾驶车辆决策研究方面，以自动驾驶车辆正常工况下的决策研究较多。ZHENG等[10]使用传统的人工神经网络模型(artifical neural network, ANN)替代决策树算法，对车辆运行状况样本数据进行训练建立了ANN驾驶决策模型；张立增[11]通过分析驾驶员控制汽车行驶方向与速度的综合决策行为的本质，提出了一种基于机理与规则的智能汽车决策行为建模方法。也有学者针对危险工况下的决策机制展开了研究，LI等[12]构建了典型的道德困境场景，通过提取关键因素来表征不同情景下的驾驶决策，为自动驾驶车辆的道德算法设计提供了依据。

以上驾驶决策机制大多针对正常驾驶工况，采用神经网络等算法需要较大的样本量，危险工况下的决策较少，决策模型中也没考虑情感强度等因素。因此本文运用泛化能力强的最小二乘支持向量机(least squares support vector machine，LSSVM)机器学习方法和粒子群智能优化算法搭建驾驶决策模型，并借鉴人工内分泌模型中的激素调节机制，以“场景设计—指标数据采集—驾驶人情感强度计算—决策模型验证”为研究路线，将情感强度融入到驾驶决策中，设计了一典型危险工况场景，采集相应的驾驶员生理、行为等指标数据，构建危险工况下的基于情感强度的驾驶决策模型，并对其进行验证。

1 实验设计

1.1 场景设计

本文以现实生活中常见的“鬼探头”场景为例，设计了如图1所示的道路交叉口实验场景，情况如下：实验车为自动驾驶车辆，位于中间车道，未行驶到停车线；最右侧车道为大卡车(体型大)，停在停止线上；左侧车道为停止的一小型乘用车，行人在人行道通行。下一时刻交通信号灯变为绿色，实验车获得了交叉口的通行权，即将驶入交叉口，但由于其视线被最右侧车道的卡车挡住，存在视觉盲区，无法关注到在道路的右侧突然出现的行人，使得正常行驶的实验车面临危险工况下的驾驶抉择难题。

图1 实验场景

1.2 实验过程

本实验共招募了60名具有丰富驾驶经验的驾驶员，其中男性驾驶员42名，女性驾驶员18名。在进行虚拟驾驶实验前，所有被试者都需要填写调查问卷，问卷内容主要包括个人驾驶习惯、驾驶经验、交通事故经历、生理和心理状况等。被试者的平均年龄是 37.7 岁(标准差为 3.91 岁)，年龄范围是 28～53岁；均持有驾驶执照及具有5 年以上的驾驶经验；均没有视觉和心理问题。在60名被试者中，有2名参与者(1 名男性，1 名女性)在过去 5 年里发生过轻微车祸，其他参与者在过去5年里没有发生过车祸。

实验设备如图2所示，包括UC-win/Road 13.0.1仿真软件、驾驶模拟器、Ergolab人机环境同步平台(生理指标数据收集、分析)等。实验过程主要包括以下3部分：

图2 实验设备

① 实验准备

工作人员对被试者进行实验说明，穿戴好传感器和电极，等待实验。工作人员查看ErgoLAB平台同步记录软件和HRV信号传感器，在人机同步监测画面中，待驾驶人HRV信号稳定后开始行驶。

② 驾驶适应性训练

为了让被试者能够熟悉驾驶模拟器的各项操作，首先安排被试者进行适应性训练，在一条宽阔的高速公路上行驶以适应车辆保持直线行驶等操作，然后被试者需要躲避三个障碍物以训练转向和制动等操作。

③ 典型危险工况下的决策实验

在不被告知即将发生的突发状况的前提下，让被试者开始驾驶。当驾驶员到达满足触发条件的位置时，路边的行人开始穿越马路。在碰撞不可避免的情况下，驾驶员会采取紧急制动、转向等措施选择碰撞目标。工作人员在ErgoLAB平台标记碰撞事件点，用于数据分析和对比。

1.3 实验数据采集

① 对实验的所有参与者进行编号，并收集性别、年龄等人口统计信息。

② 采用UC-win/Road 13.0.1仿真软件对典型场景进行虚拟场景建模，将建立的虚拟场景接入FORUM 8.0驾驶模拟器进行驾驶决策实验, 该模拟器可以实时记录目标车辆和其他交通参与者(车辆、行人等)的位置、速度、加速度、油门和制动踏板力等。

③ 主要采用ErgoLAB人机环境平台中的心率变异性(heart rate variability, HRV)模块和呼吸(respiration, RESP)模块，经滤波处理、图像反卷积、奇异点纠正、时域分析、频域分析等生成生理指标，同步到该平台。实验结束后将数据条从ErgoLAB平台导出，按被试者进行编号，转录入生理指标数据库。

2 基于人工内分泌系统的情感强度计算模型

本文选择人工内分泌模型(artificial endocrine model, AEM)计算情感强度，激素浓度的变化会使得人体的生理指标发生变化，因此可借用皮电、心电、肌电、腺体分泌等生理指标的变化来间接表示人体激素浓度的变化，以建立情感强度和生理指标强度的数学模型，解决情感强度指标难以量化的难题。

2.1 激素调节模块

本文选取驾驶员心率变异性指标HRV和呼吸指标RESP间接表征激素模块的具体指标。在人工内分泌模型中，激素在t+1时刻的浓度为t时刻浓度消逝后的数值与t+1时刻新生成的激素浓度之和[13]，如式(1)所示：

Ch(t+1)=αCh(t)+ΔCh(t+1),

(1)

式中,Ch(t+1)为激素在t+1时刻的浓度；α为激素的消逝程度；Ch(t)为激素在t时刻的浓度；ΔCh(t+1)为t+1时刻新生成的激素的浓度。

结合驾驶员生理指标的特征规律，ΔCh(t)的计算应满足以下条件：①目标距离驾驶员越远，对新生成激素浓度的影响越小；②驾驶员刹车踏板值越高，则新生成的激素的浓度越高；③上一时刻产生的激素浓度越高，对新生成激素的浓度的促进越大。因此，对人工内分泌模型中ΔCh(t)的计算公式改进如下：

(2)

式中,ΔCh(t)为t时刻新生成的激素的浓度；Lmax为驾驶员发现的障碍目标的最远距离；L为t时刻驾驶车辆距离目标障碍物的距离，取值范围为1～Lmax；B为t时刻驾驶员的刹车踏板值；Bmax为整个实验过程中的最大刹车踏板值；Ch(t-1)为激素在t-1时刻的浓度；Hmax为整个实验过程中激素浓度的最大值；Cmax为实验过程中相邻间隔内激素浓度的最大改变量。

2.2 情感强度生成模块

情感强度分为初级和高级情感强度。初级情感强度是指当人体受到外界事物刺激时产生的本能情感，其受到前一时刻产生的高级情感强度的影响。具体到本文的危险工况场景中，驾驶员生成的初级情感强度主要受驾驶员与障碍物之间的距离的影响，其公式如式(3)和(4)所示：

Pe(t+1)=β×Se(t)+ΔPe(t+1),

(3)

(4)

式中,β为情感强度的消逝程度；Pe(t+1)为t+1时刻初级情感强度；Se(t)为t时刻高级情感强度；ΔPe(t+1)为t+1时刻新生成的初级情感强度。

高级情感为初级情感经过激素调节之后的产物，其公式如式(5)所示：

(5)

式中，χ为调整系数；Se(t)为t+1时刻的高级情感强度值。

2.3 情感强度的计算流程

① 确定数据计算的时间轴：在驾驶过程中，驾驶员会不断过滤对自身没有威胁的物体，情感强度值会根据周围车辆等环境的变化有波动。驾驶车辆与路侧物体以及道路中其他交通参与者的距离是给驾驶员带来恐惧紧张等情感强度变化的主要因素，当前方突然闯入其他交通参与者(车辆、行人等)使得碰撞无法避免时，情感强度值会激增直到达到最大值。为了避免过多试验数据干扰，定义计算时间从碰撞发生前5 s开始，直到发生碰撞。

② 计算激素在各时刻的浓度：根据得到的生理指标和驾驶绩效指标数据，按照公式(2)计算激素初始浓度和下一时刻新生成的激素浓度，并不断向下更新各个时刻的激素浓度，直到发生碰撞。

③ 计算各时刻的情感强度值：利用上一时刻的高级情感强度值计算当前时刻的初级情感强度值，并结合当前时刻的激素浓度，推算得出当前时刻的高级情感强度值。

④ 筛选出情感强度最大值：分别从HRV信号和RESP信号对应的高级情感强度中筛选出最大值，取均值作为驾驶员对前方目标的情感强度值。

情感强度计算流程如图3所示。

图3 情感强度计算流程

3 危险工况下驾驶决策预测模型

3.1 数据选取与处理

针对本文的特定试验场景，选取的决策指标包括驾驶绩效指标、法律指标、道德指标、生理指标、决策指标。其中驾驶绩效指标包括当前车辆速度X1和当前车辆与前方目标的距离X2;道德指标包括前方目标类型X3、左侧目标类型X4、前方目标数量X5;法律指标为前方目标通行权X6;生理指标换算为情感强度X7;决策指标Y分为左转+刹车和刹车两种。驾驶决策的重要指标见表1。在进行预测训练之前，对采集后的一些数据进行筛选、过滤、无量纲归一化等处理，驾驶决策各影响因素的部分数据见表2。

表1 驾驶决策的重要指标

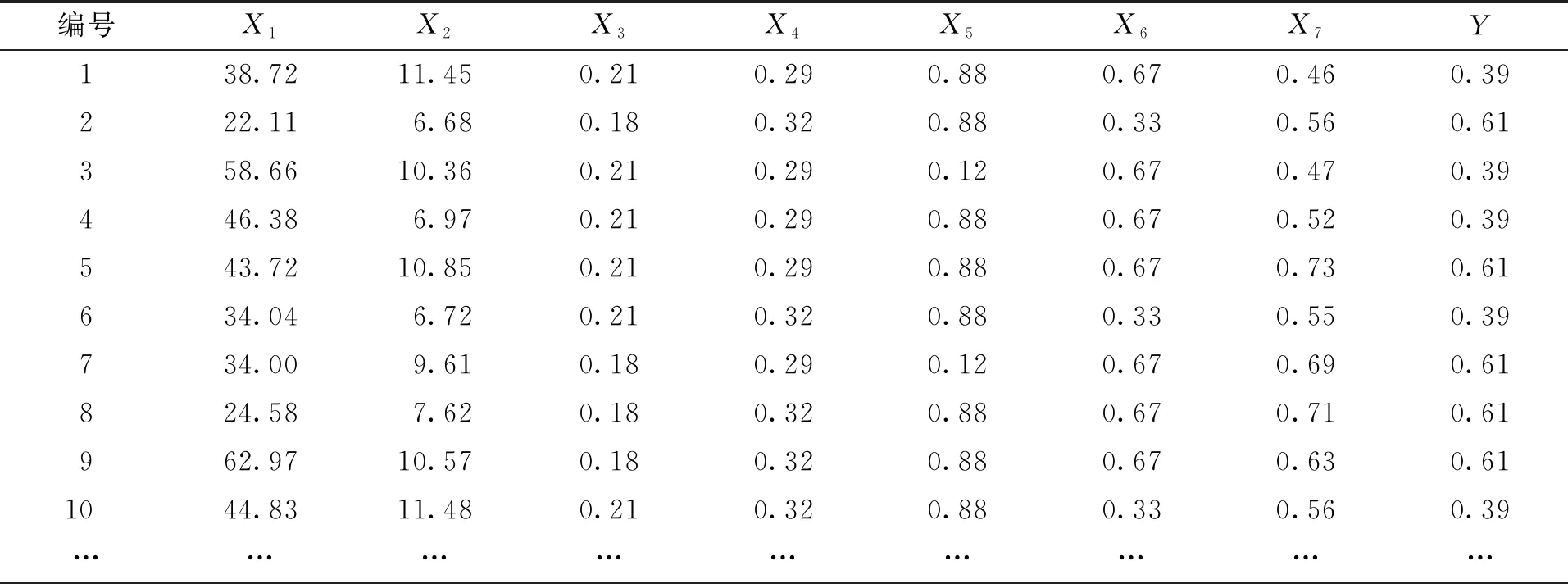
表2 驾驶决策各影响因素的部分数据

3.2 改进的PSO-LSSVM驾驶决策模型

① PSO-LSSVM模型

最小二乘支持向量机(least squares support vector machine，LSSVM)是在传统的支持向量机中引入最小二乘线性算法，在用等式约束代替不等式约束的同时，将二次方程规划问题转化为线性方程组的解，进而找到模型中输入和输出之间的函数关系。作为传统的支持向量机的一种改进模型，在有效保证识别精度同时，使得求解算法更为简单，模型求解速度更快，计算量更少[14]。LSSVM中的核函数的设计是关键，本文选择局部强的径向基(radial basis kernel，RBF)核函数，因此对LSSVM参数的优化就是对惩罚系数C和RBF核函数中的宽度参数σ进行优化。

粒子群优化算法(particle swarm optimization，PSO)是一种群智能优化算法，其基本原理是模拟鸟类的捕食行为，通过群体内的协作和信息交互来寻找最优解。PSO算法中没有过多参数的调节，操作简单，相较于传统的遗传算法具有更快的收敛速度，故本文选择PSO算法确定LSSVM模型中的待定参数。PSO-LSSVM模型优化流程如图4所示。

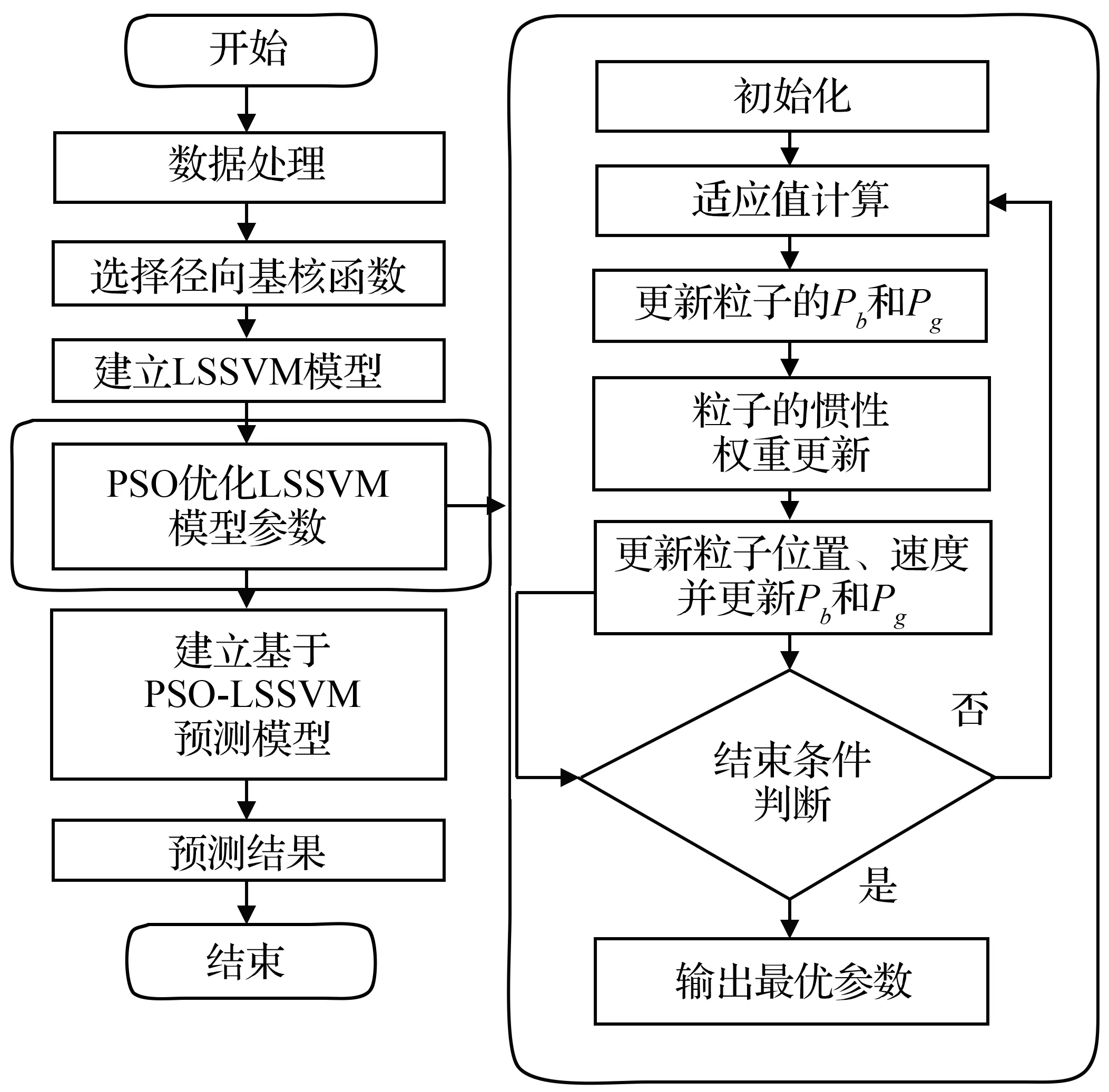
图4 PSO-LSSVM模型优化流程图

② PSO算法的改进

PSO算法中假设N维空间中有m个粒子，定义粒子i的位置xi=[xi1,xi2,…,xin]，粒子i的飞行速度vi=[vi1,vi2,…,vin]。每个粒子均能记忆自身搜寻到的最佳位置，且可根据自身经验和其他粒子的经验调整速度。定义粒子i搜索到的个体最优位置为pbest=[pi1,pi2,…,pin]，种群搜索到的全局最优位置为Gbest=[Gi1,Gi2,…,Gin]。粒子i的第n维(1≤n≤N)速度更新公式如式(6)所示：

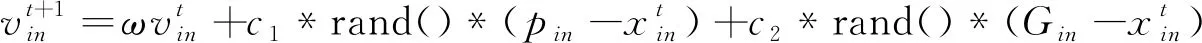
(6)

式中，ω为惯性因子;c1为粒子的个体学习因子;c2为粒子的社会学习因子，vmax为最大飞行速度，若vin超出界限则取界限值；i=[1,2,…,m]，n=[1,2,…,N]；rand()表示[0，1]之间的随机数。

传统PSO算法中的ω采用固定取值，惯性权重ω直接影响算法的性能，当ω较大时，全局搜索能力较强，局部搜索能力下降；当ω较小时则相反。因此，本文设置ω的变化如式(7)所示：

(7)

式中,ωmax和ωmin分别为惯性权重ω在整个迭代过程中的最大值和最小值；it为迭代次数；itmax为最大迭代次数。由式(7)可知，随着迭代的进行，惯性权重ω的取值呈现线性减小的趋势。

3.3 结果分析

结果分为三部分，第一部分是验证改进后PSO算法的优越性，第二部分是验证改进的PSO-LSSVM决策模型的优越性，第三部分是验证情感强度在决策模型中的作用。

① PSO算法改进前后对比

以往的研究大多采用K折交叉验证(K-CV，K-fold cross validation)的方法计算预测准确度对LSSVM的性能进行评价。具体到本文的PSO-LSSVM模型中，适应度值即K-CV的预测准确度。在本实验中选取75%的样本(270个)作为训练样本，设置粒子群种群的大小m=20，惯性权重值ω=0.8，学习因子c1=c2=2，最大迭代次数为200，根据前人的研究成果[15]，设置ωmax的取值为0.9，ωmin的取值为0.4。同时用改进的PSO算法进行对比验证，得到PSO算法优化前后对比曲线如图5所示。

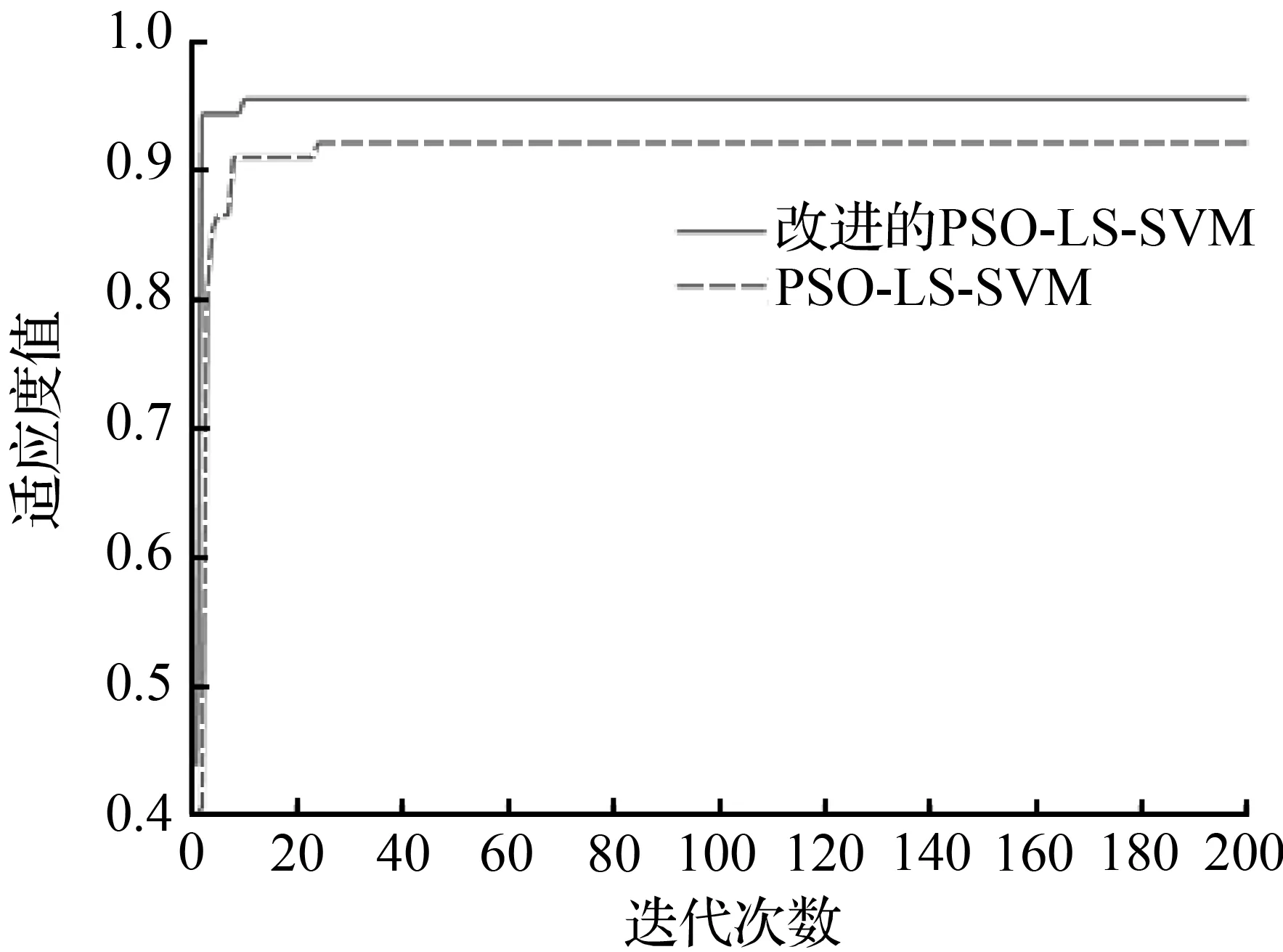
图5 PSO算法优化前后对比曲线

从图5可以看出，本文改进后的PSO算法具有更快的迭代速度和分类准确率，其中，传统PSO算法中，惩罚因子C=0.435 2，g=1.515 7，最佳适应度(cross validation accuracy, CVA)=92.5%；改进的PSO模型中，惩罚因子C=2.297 4，g=3.031 4，CVA=96.1%。

② 不同决策模型之间的对比

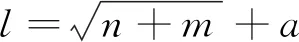
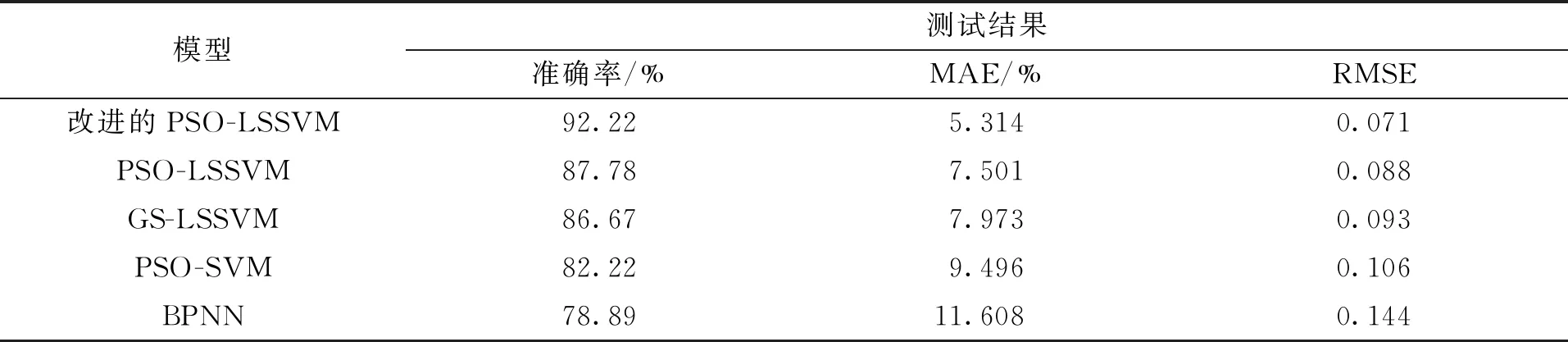
表3 不同模型的预测结果对比

分析表3中数据可知，本文提出的改进的 PSO-LSSVM 模型相较于其他预测模型，预测准确率更高。且PSO 算法与 GS 算法相比，可以对 LSSVM 模型进行更好地优化，LSSVM 模型比SVM 模型相比，预测准确率进一步提高，而传统的 BPNN 模型的预测结果相对较差。

③ 情感强度在决策模型中的作用

为了验证情感强度指标在决策预测模型中的作用，将相同数量的样本分成两类。第一类样本中包括X1-X77个输入量，第二类样本中包括不含情感强度指标X7的6个输入量。将其分别代入改进后的PSO优化算法中，其余参数和之前设置一致，得到第一类和第二类样本的适应度值分别如图6和图7所示。

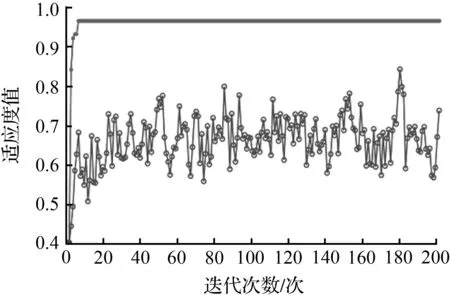
图6 第一类样本的适应度值

图7 第二类样本的适应度值

第Ⅰ类样本的最佳适应度值(CVA1)=97.13%，高于第Ⅱ类样本的最佳适应度值(CVA2)=95.96%。从图6和图7可以粗略地看出，第一类样本的平均适应度在70%左右波动，第二类样本的平均适应度在60%左右波动，说明加入输入量情感强度指标后，样本的适应性更强，表明情感强度因素对于提高模型的预测精度有一定作用。

4 结语

本文通过建立一典型的危险工况场景，利用驾驶模拟器及生理传感器等设备采集危险工况下的驾驶行为数据，分析该危险工况内驾驶决策的影响因素，建立了包括情感强度等输入指标的改进PSO-LSSVM驾驶决策模型，探究情感强度对驾驶决策的影响。

① 构建了危险工况下的目标情感强度计算模型，通过分析人类在危险工况中的本能反应，对激素调节模块和情感生成模块进行改进，将模型中难以测量的激素浓度用生理指标代替，进而计算驾驶模拟实验中驾驶员对前方目标的情感强度值，定量描述驾驶人对各目标的情感强度。

② 把情感强度融入到驾驶决策中，与驾驶绩效、道德、法律等指标作为驾驶决策模型的输入信息，采用改进的PSO算法对LSSVM模型的参数进行优化，建立了危险工况下的PSO-LSSVM驾驶决策模型，结果表明在预测模型中加入情感强度指标可以增强样本的适应性。

需要指出的是，本文仅建立了单一典型危险工况场景，后续会进一步开展多种典型危险工况下的决策研究，逐步丰富研究内容，本文的研究可为危险工况下自动驾驶车辆的拟人决策提供理论参考。