近加热壁面的双空穴对颗粒堆传热性能的影响

神英凯，郑斌，孙鹏，高腾飞，王有镗，刘永启

(山东理工大学 交通与车辆工程学院， 山东 淄博 255049)

0 引言

在物料预热、太阳能热采集、储热等过程中，普遍存在固体颗粒物的加热过程[1- 6]，同时为了防止固体颗粒物在加热过程中被氧化，常采用颗粒/加热壁面间壁式的加热方式，如外热式回转窑内壁与颗粒间的接触传热、气冷堆卵石床的传热、流化床对粗煤颗粒的预热等[7-11]。为了提高能源利用效率，开展加热壁面与颗粒堆传热过程的研究具有重要的应用价值。

在壁面与颗粒堆传热的研究中，BU等[12]研究了颗粒间分别是面接触、短圆柱接触和间隙接触时对有序堆积颗粒换热的影响，并说明了各接触方式的适用情况。GAN等[13]探究了椭球形颗粒对填充床的传热影响，研究表明椭球长宽比对有效导热系数有显著影响。MARIO等[14]探究了颗粒接触点处理方式对填充床传热数值模拟的影响，提出了一种修正桥接导热系数的模型。CHRISTINE等[15]探究了表面粗糙度对球形颗粒填充床传热性能的影响。GOVENDER等[16]探究了颗粒形状对填充床有效导热系数的影响。前人主要针对无空穴颗粒堆开展了较为系统的探索，但是由于颗粒的流动性能差，在颗粒堆中常出现空穴，特别是临近加热壁面区域，空穴的存在对颗粒堆加热过程的影响需系统探究。张仲彬等[17]通过VOF和凝固熔化模型探究了空穴对相变胶囊蓄热的影响，发现空穴的存在使蓄热过程变缓。YANG等[18]探究了随机性空穴对多孔结构传热性能的影响，研究表明随机性对努塞尔数有显著影响。SOLOMON等[19]重点研究了内部空隙位置对传热特性的影响；BADRUDDIN等[20]认为多孔介质传热已得到广泛研究，但研究不同几何形状的空穴对传热特性的影响仍是一个广阔的领域。ZHENG等[21]采取数值模拟与实验验证相结合的方式，探究了单空穴存在对颗粒堆传热特性的影响。赵强[22]研究了单空穴在颗粒堆内位置变化对颗粒堆传热性能的影响，发现临近壁面的空穴与颗粒堆内部的空穴对颗粒堆传热性能的影响不同。现有研究多针对空穴在颗粒堆内部时开展的，空穴在临近加热壁面时对颗粒堆传热性能的影响尚缺乏系统研究。因此，本文选取颗粒堆中出现几率最大的双空穴为研究对象[23]，探究近加热壁面的双空穴对颗粒堆传热性能的影响规律，以期为相关加热设备的设计提供基础理论依据。

1 模型建立与验证

1.1 物理模型

实际颗粒堆形状多样复杂，为了更好的描述空穴颗粒堆传热特性和提高计算速度，构建模型时进行了以下简化假设：①颗粒堆积方式为简单立方堆积；②气相与颗粒相之间的相对流速较低，对流换热影响较小可以忽略[24]，只考虑导热及辐射换热；③为使颗粒堆准二维化，选取等直径圆形颗粒替代实际颗粒；④固相颗粒间采用面接触方式[12]。根据以上假设，所建立的双空穴颗粒堆模型如图1所示。

图1 双空穴颗粒堆模型

1.2 数学模型

颗粒堆模型的传热方式主要包括颗粒内部导热、颗粒与壁面导热、颗粒间辐射换热及颗粒与壁面间的辐射换热，因此根据简化后的模型，双空穴颗粒堆传热过程可简化为导热-辐射过程，相关控制方程如式(1)：

(1)

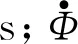
固体颗粒间气体与固体颗粒间接触面为耦合壁面边界条件，耦合面上热流密度及温度连续分布，如式(2)、式(3)所示：

Tws=Twf，

(2)

qws=qwf，

(3)

式中，T是颗粒某一时刻的温度；q是热流密度；下标w表示流固交界面；下标s表示固体；下标f表示流体。

颗粒之间及颗粒与换热壁面的辐射换热采用DO辐射模型，DO辐射模型相比于其他辐射模型，求解精度更高，考虑的因素更全面，在满足计算要求的前提下，对小尺度空间内的辐射计算有更好的精度，其控制方程如式(4)至式(6)所示：

(4)

(5)

式中，εw为颗粒表面发射率；Tw为颗粒表面温度，K；qin为入射到颗粒表面的辐射热流，W/m2。

(6)

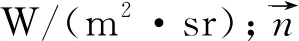
1.3 初始条件与边界条件

颗粒直径为16 mm、厚度为3 mm，颗粒之间的面接触系数为0.12，颗粒数目为400。为了更清楚地研究空穴对传热的影响且避免两侧绝热壁面的影响[21]，颗粒堆按20×20布置，所选研究区域为第5列至第15列。模型利用软件Fluent19.2模拟，收敛标准为当迭代计算的能量残差为10-6以下时，迭代计算结束，计算收敛。

颗粒相与气相的初始温度为298 K，热壁面温度为673 K，冷壁面温度为298 K，颗粒密度为7 840 kg/m3，比热及导热系数由式(7)、式(8)给出：

Cp=450.41+0.248 95T-0.001 69T2+4.833 41×10-6T3-5.356 45×10-9T4+2.139 49×10-12T5，

(7)

λ=56.444 97-0.019 33T-1.507 38×10-5T2+8.742 44×10-9T3，

(8)

式中，Cp为颗粒比热容，J/(kg·K)；T为颗粒温度，K；λ为导热系数，W/(m·K)。

模型中，除去冷热壁面，其余壁面均为理想绝热壁面。颗粒间接触面为固/固耦合壁面，颗粒与壁面接触面为固/固耦合壁面，气相与固相颗粒及壁面接触面为气/固耦合壁面。

1.4 实验系统与模型验证

为了验证计算模型，搭建了颗粒堆传热性能实验系统，该系统由颗粒堆传热系统、加热系统、冷却系统、保温系统与数据采集系统组成(图2)，实验颗粒尺寸与模型尺寸一致，温度测点布置情况如图3所示。加热系统为5 kW陶瓷管加热器，采用红外测温仪对加热板表面进行温度测试，加热板在设定温度400 ℃情况下，温度在394～403 ℃变化，最大相对误差为1.5%，说明加热系统可稳定提供热量。数据采集系统的热电偶采用OMEGA公司的CO3-K型贴片热电偶，精确度为±1.5 ℃，温度范围为0～450 ℃，满足本实验要求。实验步骤：首先接通电加热板电源及开启节流阀，通过温控开关和流量计控制冷热壁面温度分别为25 ℃和400 ℃，通过流量计来控制冷却流体流速以达到有效的冷却效率。然后通过计算机数据监测软件实时观察测点的温度数据，当温度数据波动小于1 ℃时，认为实验传热已达到稳态，稳态后采集温度数据。

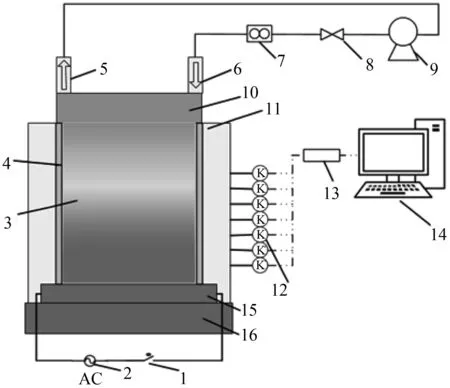
1-温控开关；2-交流电源；3-缺位空穴颗粒堆；4-陶瓷挡板；5-出水口；6-进水口；7-流量计；8-节流阀；9-水泵；10-冷却水箱；11-保温层；12-温度传感器；13-数据采集卡；14-计算机；15-加热板；16-耐火砖

图3 温度测点分布

图4为实验值与模拟值的对比图。由图4知，当传热过程达到稳态后，实验与计算值的吻合度较高，两者之间相对误差范围为0.15%～3.36%，相对误差均在合理范围(5%)之内，说明本文建立的传热模型可靠。

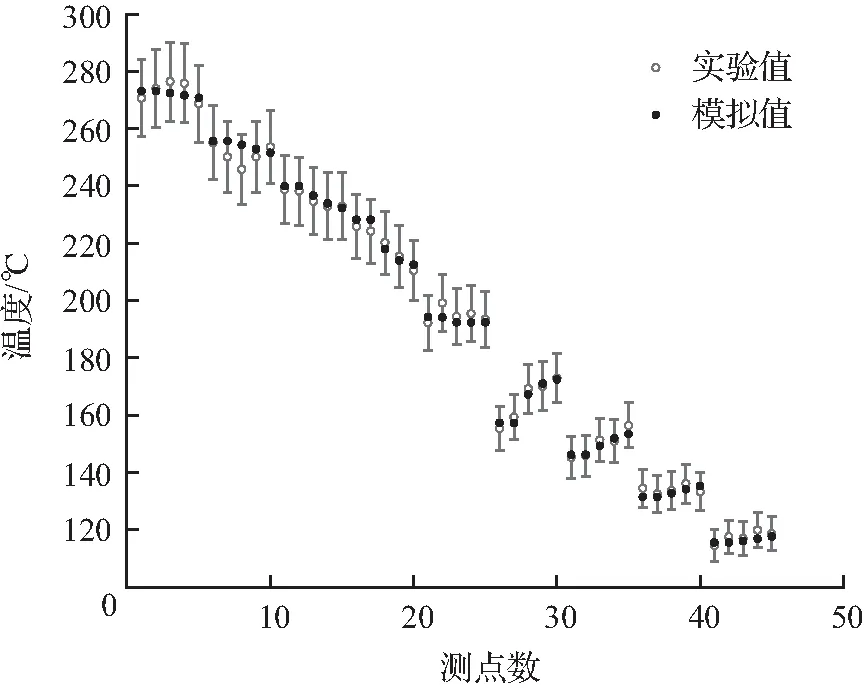
图4 实验与模拟值对比

1.5 研究参数与范围

① 空穴与加热壁面距离：表示空穴下端与加热壁面之间距离，用两者之间的颗粒层数来表征，例如，当空穴与加热壁面距离为1时，说明空穴与加热壁面之间存在1层颗粒，如图5所示。该参数的变化范围为0～5。

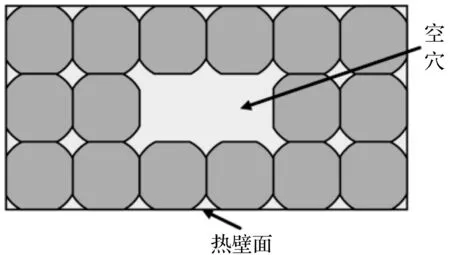
图5 空穴与加热壁面距离为1的示意图

② 空穴相对距离：表示两个空穴之间的距离，用两个空穴之间的颗粒层数来表征，例如，空穴相对距离为1时，说明两空穴之间存在1层颗粒，如图6所示。该参数的变化范围为0～8。

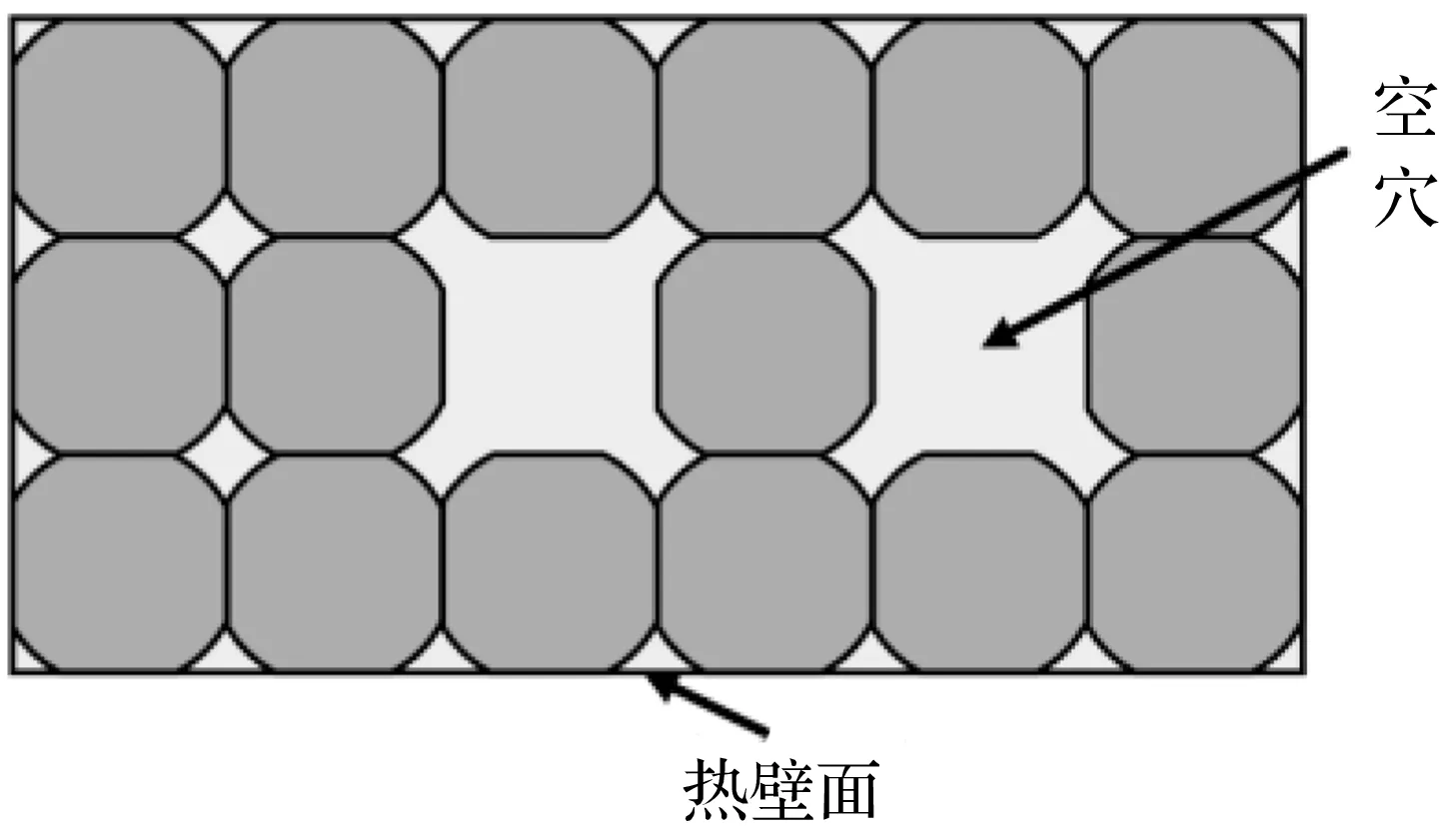
图6 空穴相对距离为1的示意图

1.6 评价指标

选取了总热流量、研究区域热流量、表观热阻、研究区域表观热阻、空穴影响区域和空穴影响区域面积比作为本文的评价指标，具体如下：

① 总热流量：空穴颗粒堆换热过程的总加热功率为总热流量。

② 研究区域热流量：所选研究区域换热过程的总加热功率为研究区域热流量。

③ 表观热阻：颗粒堆阻止热量传递的能力，用冷热壁面温度差值与总热流量的比值表征，计算方程如式(9)所示：

(9)

式中，Ra为表观热阻，K/W；ΔT为冷热壁面温度差值，K；Qa为总热流量，W。

④ 研究区域表观热阻：所选研究区域颗粒堆阻止热量传递的能力，用冷热壁面温度差值与研究区域热流量的比值表征，计算方程式如式(10)所示：

(10)

式中，Rb为研究区域表观热阻，K/W；ΔT为冷热壁面温度差值，K；Qb为研究区域热流量，W。

⑤ 空穴影响区域：受空穴影响，颗粒堆温度出现变化的区域，以冷热壁面温差的1%(3.75 ℃)作为温度影响区域的评估指数。

⑥ 空穴影响区域面积比：空穴影响区域面积与固相颗粒和气相总面积之比，如式(11)所示：

(11)

式中，rs为空穴影响区域面积比；SΔT为空穴影响面积，m2；St为固相颗粒及气相总面积，m2。

2 结果与分析

2.1 空穴与加热壁面距离变化对传热性能的影响

图7为空穴与加热壁面距离变化对研究区域热流量与表观热阻的影响。随着空穴与加热壁面距离增加，研究区域热流量呈先减小、后增加的趋势，当空穴与加热壁面距离为1时研究区域热流量值最小，为14.64 W。随着空穴与加热壁面距离的增加，研究区域表观热阻先增加、后减小，当空穴与加热壁面距离为1时研究区域表观热阻最大，为25.61 K/W。当空穴与加热壁面距离为0时，与加热壁面直接接触的颗粒数量减少，使进入颗粒堆的传热通道减少，导致颗粒堆热阻较大，如图8(a)所示。当空穴与加热壁面距离由0增加到1时，一方面，与加热壁面直接接触的颗粒数量增加，使进入颗粒堆的传热通道增加，有利于热量传入颗粒堆；另一方面，由于空穴下方仅有一个颗粒，通过该颗粒进入颗粒堆的热量由于受空穴的阻碍作用，只能通过相邻颗粒的传热通道“绕流”传递下去，既使该部分热量的传热路径增加，又使相邻颗粒传热通道发生拥挤，导致颗粒堆内热量传递困难，如图8(b)所示。在这两方面综合影响且第二方面原因影响较大的作用下，使颗粒堆的热阻增加。随着空穴与加热壁面距离的继续增加，空穴下方颗粒数增加，可“分流”热量的传热通道数量增加，导致空穴对颗粒堆传热能力的阻碍影响减小，颗粒堆热阻下降。

(a) 研究区域热流量

(a) 空穴与加热壁面距离为0

图9为空穴与加热壁面距离变化对区域及区域面积比的影响。随着空穴与加热壁面距离增加，影响区域范围大小先增大、后减小，当空穴与加热壁面距离为1时影响区域最大，如图9(a)所示。空穴对下方的影响区域面积远小于上方，这是因为下方区域离加热壁面距离近，热量先传入下方区域，而在空穴对热流的阻碍作用下，下方存在热量的积聚，导致该区域温度升高，温差值减小。随着空穴与加热壁面距离的增加，空穴影响区域面积比先增加、后减小，当空穴与加热壁面距离为1时影响区域面积比最大，为19.77%，如图9(b)所示。这与研究区域表观热阻的变化相对应，此时研究区域的热流通道最狭窄，热流“分流”困难，对颗粒堆传热的阻碍作用最强，导致热量更难以传递，因此出现空穴影响区域面积比的最大值。

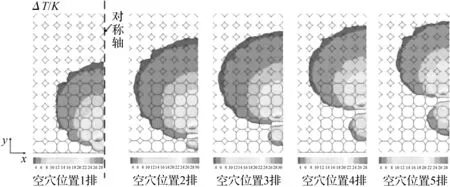
(a) 对区域的影响

2.2 双空穴相对距离变化对传热性能的影响

图10为空穴相对距离变化对总热流量与表观热阻的影响。随着空穴相对距离增加，加热壁面的总热流量增加，但增加趋势逐渐平缓。随着空穴相对距离增加，颗粒堆表观热阻减小，但减小趋势逐渐平缓。主要原因是当空穴的间隔距离较小时，空穴间的传热途径少，传热“分流”的阻力大，导致颗粒堆的热阻较大。随着空穴的间隔距离增加，可用来传热的通道增加，传热“分流”的阻力减小，这使颗粒堆热阻逐渐减小，使空穴对颗粒堆区域的影响范围逐渐变得扁平，并呈现缓慢分离的趋势，当空穴间隔增加至8倍粒径时，双空穴之间的相互影响消失，如图11所示。

(a) 总热流量

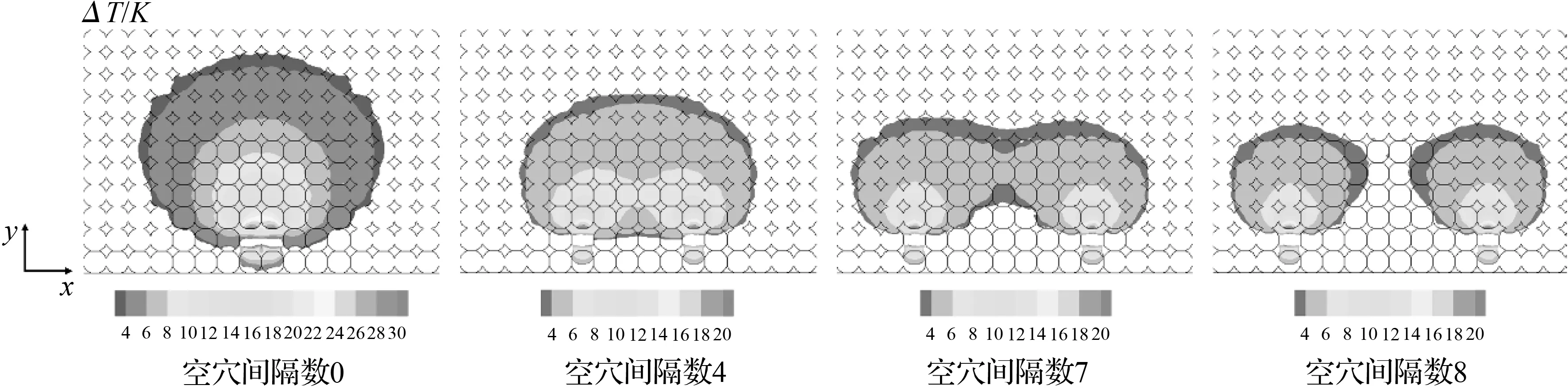
图11 空穴相对距离变化对区域的影响

3 结论

针对含双空穴的颗粒堆，对近加热壁面的双空穴对颗粒堆传热性能的影响进行了系统研究，主要结论如下：

① 随着双空穴与加热壁面距离增加，研究区域热流量呈现先减小、后增加的趋势，研究区域表观热阻呈现先增加、后减小的趋势，空穴影响区域范围和空穴影响区域面积比均先增加后减小。当空穴与加热壁面距离为1时，出现最大空穴影响区域范围，此时研究区域热流量有最小值为14.64 W，研究区域表观热阻有最大值为25.61 K/W，空穴影响区域面积比有最大比率为19.77%。

② 随着双空穴相对距离增加，加热壁面总热流量呈现增加趋势，表观热阻呈现减小趋势，但变化的趋势逐渐平缓，空穴影响范围逐渐变得扁平并缓慢分离，当双空穴相对距离为8倍粒径距离时，双空穴之间的相互影响消失。

③ 在设计和制造加热设备时，应尽量避免空穴出现在与加热壁面距离为1的位置，该位置的空穴会显著降低物料的加热效果，可以考虑将加热设备的加热板设计为波纹状或矩阵波形等形状。此外，尽可能的增加空穴的相对距离也对增强换热效果有显著影响，可以获得较好的物料加热效果。