一种改进的K-means入侵检测算法∗

张珂嘉 黄树成

（江苏科技大学计算机学院 镇江 212003）

1 引言

随着网络技术的不断发展和广泛应用，网络安全问题越来越受到人们的关注。入侵检测作为一项网络与信息安全领域的重要技术，已经成为了网络安全体系中一个重要组成部分。入侵检测系统常用的检测方法有误用检测和异常检测［1］。误用检测是一种检测计算机攻击的方法，它可以模式匹配已知的攻击行为，所以具有较低的误报率，但由于网络环境不断变化，新类型的攻击层出不穷，导致误用检测方法具有较低的检测率；异常检测是检测入侵者异于正常主体的活动，具有较高的检测率，局限在于并非所有的入侵都表现为异常，因此误报率偏高。

大数据时代，随着信息技术的快速发展，数据量急速增长。从海量的数据中挖掘出有效的信息和知识是数据挖掘技术的特征。聚类分析是数据挖掘中的一个重要的研究领域领域［2］。它将对象的集合按照一定规则进行分组，这满足了入侵检测中异常检测的需求：将入侵的异常行为同正常活动进行区别，从而达到入侵警告的目的。因此人们将聚类分析引入到入侵检测研究中。

2 Canopy-K-means算法

本章节将介绍传统K-means算法和Cano⁃py-K-means算法的基本原理与优缺点。

2.1 K-means算法原理

K-means算法是一种基于划分的无监督的聚类算法，利用数据对象间的距离作为相似性的评价指标［3］。聚类过程是一个不断迭代的过程，对数据点进行簇划分和对簇的中心点不断调整交替进行，从而实现不同簇间相似度低，簇内数据相似度高的效果。

K-means算法的执行步骤：

假设一个数据集D，其中有n个数据对象，每个数据对象含有p个特征属性，即Di=(Di1，Di2，Di3，…，Dip)，Di∈D，1≤i≤n，需要聚类的个数为K，且

K＜n。

1）根据实际应用场景，用户输入需要聚类的个数K。随机选择K个数据对象作为初始聚类中心；

2）对于每个数据对象Di，计算其到各个聚类中心的欧式距离，将Di划分到聚类中心的欧式距离最小值的聚类中，据此得到k个聚类C1，C2，C3，…，Ck；

3）对于每个聚类Ci（1≤i≤k），根据式（1）重新计算K个聚类的聚类中心；

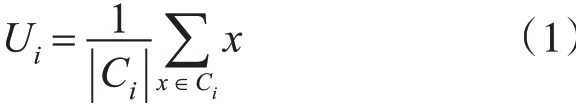
4）若重新计算的K个质心位置变化，则重复2）、3）步骤直至聚类中心不再变化。

因其算法简洁、易于实现、聚类效果较好，被大量应用在入侵检测领域。但它在实际应用过程也存在不足之处：

1）K-means算法的聚类簇数量需要人为指定，不同的k值对聚类结果会产生非常大的影响；

2）由于每个簇的初始质心都是随机产生的，易受噪声点干扰，易导致聚类结果不稳定和聚类质量不高，陷入局部最优解等问题。

2.2 Canopy-K-means算法原理

Canopy-K-means算法是一种改进的K-means算法。它是在K-means算法的基础上，先对数据进行“粗聚类”，再由K-means算法进行“细聚类”，从而达到聚类更精确的目的［4］。

Canopy算法的执行步骤：

1）将原数据集集合化为一个List，并设置T1、T2（T1>T2）；

2）从List集合中随机选出一个数据对象p，若当前没有Canopy，则p直接作为一个新的Canopy；若存在Canopy，则计算p到Canopy的欧式距离d；

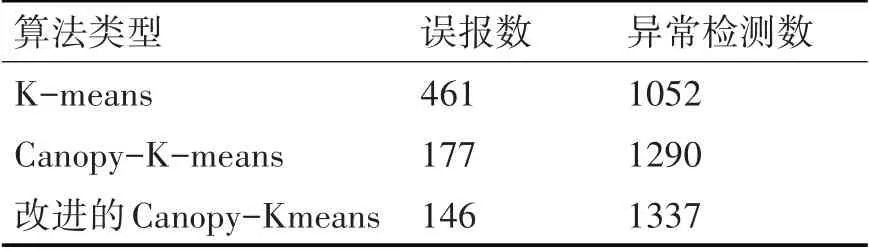
3）当d

4）重复2）、3），直至List为空；

5）将Canopy的数量和Canopy的中心质心作为K-means算法的初始质心数量k和初始质心进行聚类。

图1 Canopy聚类示意图

Canopy-K-means算法的优点在于：

2）每一个数据对象都至少被划分到了一个Conapy中；

3）一定程度上缓解了初始质心敏感的问题。

但是Canopy-K-means算法仍然存在不足之处：

1）数据集中噪声点也会被划分入Canopy，会对最终的聚类结果产生较大的影响；

2）每个Canopy的中心点依然为随机选取，仍然会对聚类结果产生较大的影响；

3）T1、T2的大小难以确定；

4）由于在K-means算法的基础上多进行了一次“粗聚类”，在实际应用中耗时会增加。

通过分析电子邮件的语言特征、结构特征与格式特征，利用支持向量机做分类算法，分析出作者的写作风格，从而建立作者身份识别模型，当需要识别某一封电子邮件时，将待识别的电子邮件通过建立的作者识别模型即可得到结果。通过测试集的电子邮件结果显示，此方法用于中文电子邮件作者身份识别，具有较高的可行性与可靠性。本文与之前学术界相关研究比较，具有以下特点：

3 改进Canopy-K-means算法

本章节将从抗噪性、初始质心选择、算法运算过程三个方面对Canopy-K-means算法进行改进。

3.1 优化噪声处理能力

Canopy-K-means算法，在执行过程中，会因为选择噪声点作为Canopy的中心点，导致聚类结果产生较大的差异，所以增强Canopy-K-means算法的抗噪能力十分必要。本文在选取Canopy之前，对数据集进行划分，从而增强算法的抗噪能力［5～6］。

定义1设数据集D，Di=(D1，D2，D3，…，Dn)，Di∈D，定义数据对象Di到其他数据对象的欧式距离和为

其中‖‖2表示欧式距离的平方。

定义2设数据集D，Di=(D1，D2，D3，…，Dn)，Di∈D，

定义数据集中数据对象到其他数据对象的平均距离和为

计算数据集中每个数据对象到其他数据对象的欧式距离平方Sum（Di）和数据集的距离和的均值Avg（D）；去除Sum（Di）>Avg（D）的数据对象，即去除数据集中的噪声点，由此得到一个新的数据集D'，并用D'进行后续聚类操作。

3.2 优化初始质心

在Canopy-K-means算法执行过程中，每一个Canopy的中心点都为随机生成。为了避免聚类陷入局部最优解，初始中心点随机性问题，本文引入“最大最小原则”对Canopy-K-means进行优化，提高聚类的准确性。

“最大最小原则”的基本思想［7］是：确保任意两个Canopy中心点的距离足够远。即假设计算m+1个Canopy中心点，除已知的m个质心外，计算其余每个数据对象到已知质心的最短距离，取其最小值；然后取最短距离中的最大值对应的数据对象作为第m+1个初始质心［8～9］。则Cm+1个质心可用公式表示为

在实际应用过程中，选取的Canopy中心点并不是最终K-means的聚类中心，所以为了避免全局求解，节省运算开销，本文取距离坐标原点最近、最远的两个数据对象为初始质心。

根据“最大最小原则”的规律：当Canopy个数小于或大于最优聚类个数时，Cm+1变化幅度较小；当Canopy个数接近或等于最优聚类个数时，Cm+1变化幅度明显；因此定义深度D（m）来描述Cm变化幅度。

当式（6）取最大值时，此时m即为最优聚类个数。有研究表明，聚类个数（N为数据规模）［10］。同时为了保证聚类中心点都落在Canopy范围内，将T1设置为Cm［11］。

3.3 优化K-means运算过程

在将由Canopy算法得出的初始质心和K代入K-means算法的过程中，由于Canopy算法特性，每一个数据对象至少在一个Canopy中，可能会存在多个Canopy中并且Canopy具有簇间相似度低，簇内相似度高的特性，所以在进行K-means算法的聚类过程中，不需要计算不同Canopy间的相似度，只需要计算数据对象所在Canopy的相似度，将其归入相似度高的Canopy中即可。在Canopy重叠较少的环境下，可明显地减少K-means算法的迭代次数。

3.4 基于Canopy-K-means的改进算法

将上述优化处理有机结合得到一种新的Cano⁃py-K-means算法。具体算法流程为

1）对原始数据集D进行抗噪处理，得到新数据集D'，并放入集合List中；

2）若集合Q为空，则选取List中距离坐标原点最近的数据对象，放入Q中；

3）若集合Q不为空，则选取距离Q中所有数据对象距离最短中的最大者，放入Q中；

5）计算深度D（m），得出最优聚类个数K和T1，并截取Q中前K个数据对象作为初始质心；

6）根据T1，将非中心点的数据对象作上标记；

7）将得到的初始中心点、K、Canopy集合代入优化的K-means算法进行聚类。

4 实验研究与结果分析

本章节将介绍仿真实验过程涉及到的实验模型、数据集、算法评价指标以及实验结果分析。

4.1 实验模型及数据集选择

本文采用的入侵检测模型如图2。

图2 入侵检测模型示意图

本文选取Snort入侵检测系统进行仿真实验，采用kddcup.data_10_percent数据集作为网络数据［12～13］。该数据集为KDD Cup99的10%抽样，其中包含正常数据和攻击数据。攻击数据中分为DOS攻击、Probing攻击、U2R攻击和R2L攻击［14～15］。实验前，先对数据集进行标准化、归一化处理［16］，然后从中随机选取7428条正常数据和1560条异常数据（含21类攻击行为）作为数据集D，进行多次实验取均值。

4.2 实验结果评估指标

运用检测率、误报率，两个常用的入侵检测评判指标来判断K-means算法改进前后的性能。

1）检测率

检测率是用来评价算法对入侵攻击检测程度的指标，可以有效的反应出该算法对入侵攻击的检测情况。通常情况，检测率越高，算法对入侵攻击的识别效果越好。具体公式如下：

2）误报率

误报率是用来评价算法对正常活动误判的指标，通常情况，误报率越低，说明算法对区分正常活动和异常活动更精准。具体公式如下：

4.3 结果分析

经式（7）和（8）可得三种算法的误报率和检测率，如表2所示。

表2 实验测试对照表

从表1和表2可以看出改进后的Canopy-Kmeans算法相比于传统的K-means算法和Cano⁃py-K-means算法均具有更低的误报率和更高的检测率，改进后的Canopy-K-means算法性能更优。

表1 入侵检测结果

5 结语

本文针对传统K-means算法需要初始质心敏感、需要人为指定K、抗噪能力差，提出了改进的Canopy-K-means算法。通过实验结果可知，改进后的Canopy-K-means算法性能明显优于传统K-means算法和Canopy-K-means算法，因此可将改进的Canopy-K-means算法应用于入侵检测，以提高入侵检测的性能。下一步研究将针对改进的Canopy-K-means算法的时间复杂度、耗时进行深入探索。