形式概念分析中的面向对象概念约简
智慧来,李逸楠
(河南理工大学 计算机科学与技术学院,河南 焦作 454003)
0 引言
形式概念分析理论是对领域本体进行抽象描述,并且以概念的形式呈现[1]。经过多年的研究探索,该理论已经在概念格构造[2]、属性约简[3-7]、概念约简[8-10]、规则获取[11]、粒计算[5,12-17]等方向获得了大量的研究成果,广泛应用于信息检索、数据挖掘、知识发现、人工智能等诸多领域。
在当今大数据时代,知识获取变得愈加复杂。众所周知,概念格的构造本质上是一个NP-hard问题[18]。因此,在保持概念格某种性质不变的前提下进行概念格的约简就显得极其重要。围绕概念的约简,已经有众多学者提出了各自的想法[3-10]。Keprt与Belohlavek等[19-20]将形式概念分析理论引入矩阵分解,并提出了一种计算理想因子的方法,从而开启了利用形式概念分析理论实现矩阵分解的研究。
粗糙集理论是对象刻画的另一种有效理论,通过采用近似的方式以处理数据的不确定性[21]。形式概念分析理论和粗糙集理论之间有着极强的互补性[22]。姚一豫[23-24]基于粗糙集理论,定义了面向对象概念和面向属性概念,并且深入讨论了两者的性质。相比较于形式概念,面向对象概念刻画的是外延中对象集的必然属性,与形式概念表达的共同属性语义截然不同[14]。鉴于面向对象概念与形式概念同样具有广泛的应用场景[14-15],因此亦有必要研究面向对象概念的约简问题。
本文研究如何在重构原形式背景二元关系的前提下进行面向对象概念的约简。具体地,通过减少面向对象概念,寻找尽可能少的面向对象概念,从这些面向对象概念出发,可以重构原形式背景的二元关系。在本文中,首先提出面向对象概念框架下的因子分解和面向对象概念约简,然后讨论面向对象概念约简的存在性及判定方法,并提出一种面向对象概念约简求解算法,最后依据面向对象概念在约简过程中所起的不同作用,将其分为核心、相对必要和不必要面向对象概念。
1 基础知识
形式背景是领域本体的抽象描述。假定,用G表示领域本体中的全部对象,并且用若干属性M刻画这些对象。具体地,若对象x具有属性a,则用I(x,a)=1表示,否则记为I(x,a)=0。此时,得到的三元组(G,M,I)即为该领域本体的形式背景。
在本文中,对于单元素集合,为了方便起见,只列出元素并省略大括号。例如,用x表示集合{x}。
定义1[24]797设K=(G,M,I)为一个形式背景,x∈G,a∈M,X⊆G,A⊆M,定义算子如下:
x*={a|a∈M,I(x,a)=1},a*={x|x∈G,I(x,a)=1},
X□={a∈M|a*⊆X},A◇={x∈G|x*∩A≠∅}。
此外,令上标“c”表示一个集合的补集。例如,Xc=G-X,Ic=G×M-I。
定义2[24]797设K=(G,M,I)为一个形式背景,X⊆G,A⊆M。若X=A且A=X□,则称(X,A)是一个面向对象概念,并称X和A分别是这个面向对象概念的外延与内涵。进一步,称所有面向对象概念形成的格结构为面向对象概念格,记作OL(K)。
例1表1中的形式背景K=(G,M,I)对应的面向对象概念一共有13个,如表2所示,对应的面向对象概念格如图1所示。
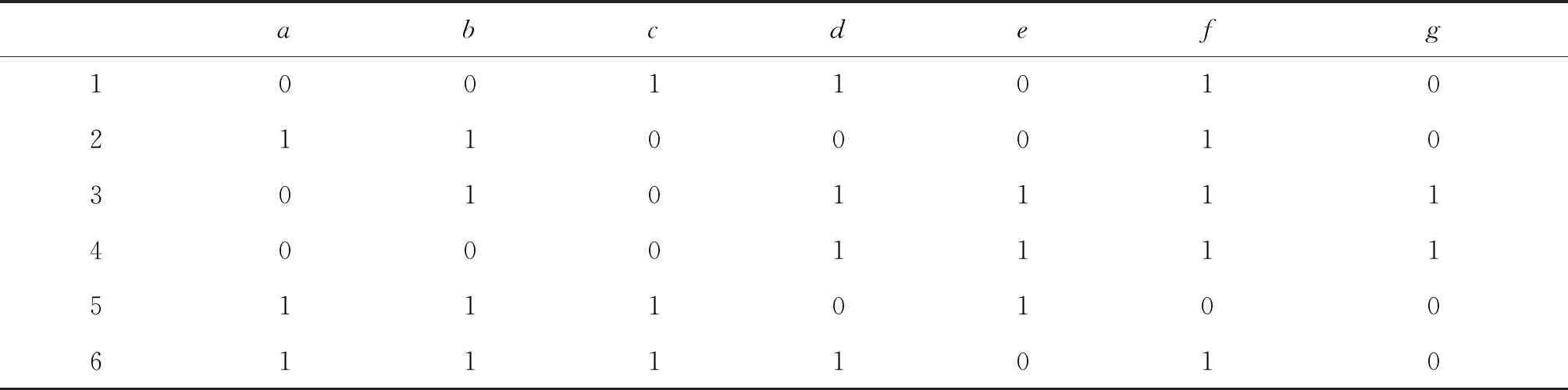
表1 形式背景K=(G,M,I)

表2 形式背景K的全体面向对象概念

图1 形式背景K的面向对象概念格
2 面向对象概念约简及特征
本节具体研究如何在重构原形式背景二元关系的前提下进行面向对象概念的约简。为了叙述方便,下文将省略此前提,简述为“面向对象概念约简”。
2.1 面向对象概念框架下的因子分解
设Un×k,Vk×m,Wn×m分别为n×k,k×m,n×m布尔矩阵,通过寻找尽可能小的k,使得Wn×m=Un×k∘Vk×m成立。在文献[25]中,称Un×k∘Vk×m为布尔矩阵乘积,并称这一过程为布尔因子分解。
下文将通过引入面向对象概念作为因子来实现这一过程。
定义3设OL(K)为形式背景K=(G,M,I)的面向对象概念格,F⊆OL(K)。若
且F中的元素最少,则称F中的元素为理想因子,并称这一过程为面向对象概念框架下的理想因子分解。
实际上,理想因子分解与布尔因子分解有着直接的对应关系。若采用布尔矩阵W表示形式背景K,用F构造布尔矩阵U与V,则有Wc=U∘V,且布尔矩阵U的列数最少。这里,Wc=E-W,E表示元素全为1的矩阵。
具体地,记G={x1,x2,…,xn},M={a1,a2,…,am},F={(X1,A1),(X2,A2),…,(Xk,Ak)}则布尔矩阵Un×k=(uij)n×k和Vk×m=(vij)k×m中的任一元素分别表示为:

例2(续例1)通过计算可知,例1中的形式背景存在理想因子c2,c4,c6,c8,c9,并且由这些理想因子可以得关于Wc的布尔因子分解。
2.2 面向对象概念约简
首先,定义面向对象概念约简如下。
定义4设OL(K)为形式背景K的面向对象概念格,F⊆OL(K)。若

性质1任意形式背景至少存在一个面向对象概念约简。
证明令K表示任意一个形式背景。若对任意的面向对象概念(X,A)∈OL(K),有
则OL(K)本身就是面向对象概念约简。

若对任意的面向对象概念(Xj,Aj)∈F,有
则F是面向对象概念约简;否则,需要进一步探究F1=F-{(X2,A2)}的约简。
重复上述过程,且鉴于OL(K)是有限集,可知K至少存在一个面向对象概念约简。
定义5[26]设S是由有限集D的子集构成的集合。S的一个碰撞集H是D的一个子集,使得对任意的S′∈S有H∩S′≠∅。进一步,若不存在S的另外一个碰撞集H′使得H′⊂H,则称H是S的一个极小碰撞集,并用hit(S)表示S的全体极小碰撞集。
例如,令S={{1},{2,3},{2,4}}则有
hit(S)={{1,2},{1,3,4}}。
设OL(K)为形式背景K的面向对象概念格,(xi,ai)为任意的二元关系,定义集合族SK如下:
Sk={{(X,A)∈OL(K)|(xi,ai)∈Xc×A}|(xi,ai)∈Ic},
则计算K的全体面向对象概念约简等价于求Sk的全体极小碰撞集hit(Sk)。
基于此,下面给出一种面向对象概念约简求解算法,如算法1所示。通过算法1,我们可以得到给定形式背景的全体面向对象概念约简。
算法1形式背景K的全体面向对象概念约简求解算法
输入:形式背景K。
输出:K的全体面向对象概念约简。
步骤1:建立K的面向对象概念格OL(K);
步骤2:对于OL(K)中的每一个面向对象概念,构造SK={(X,A)|(xi,ai)∈Xc×A}|(xi,ai)∈Ic};
步骤3:计算hit(Sk);
步骤4:输出hit(SK)中的所有元素并编号,即为形式背景K的全体面向对象概念约简,算法结束。
例3(续例1)对于表1中的形式背景K,使用算法1,通过构造SK,并计算hit(SK)即可得到K的全体面向对象概念约简。具体地:
首先,对于OL(K)中的每一个面向对象概念,为了方便起见,我们用表2中的序号指代,可以得到集合族
SK={{c5,c8,c11},{c5,c8},{c5,c9},{c5,c9,c12},{c4,c10},{c4,c7{c4,c9},{c4,c7,c9,c12},{c6,c11},{c6,c10},{c3,c6,c8,c11},{c3,c8},{c3,c6,c10},{c2,c7},{c2},{c2,c7,c12},{c9},{c9,c12}};
其次,计算
hit(SK)={{c2,c4,c6,c8,c9},{c2,c3,c4,c5,c6,c9},{c2,c4,c8,c9,c10,c11},{c2,c6,c7,c8,c9,c10},
{c2,c7,c8,c9,c10,c11},{c2,c3,c4,c5,c9,c10,c11},{c2,c3,c5,c6,c7,c9,c10},{c2,c3,c5,c7,c9,c10,c11}};
最后,输出hit(SK)中的所有元素并编号,即为形式背景K的全体面向对象概念约简。最终输出结果如下:
F1={c2,c4,c6,c8,c9},F2={c2,c3,c4,c5,c6,c9},F3={c2,c4,c8,c9,c10,c11},
F4={c2,c6,c7,c8,c9,c10},F5={c2,c7,c8,c9,c10,c11},F6={c2,c3,c4,c5,c9,c10,c11},
F7={c2,c3,c5,c6,c7,c10},F8={c2,c3,c5,c7,c9,c10,c11}。
实际上,对任意的Fi∈{F1,F2,…,F8},有
(3,a),(3,c),(4,a),(4,b),(4,c),(5,d),(5,f),(5,g),(6,e),(6,g)}=Ic。
下面给出面向对象概念约简的性质。
一是扎实开展惠企走访,及时输血民营企业。受宏观经济下行压力加大等因素的影响,民营企业经营面临多重困难。金融机构要扛起支持民营企业的责任与担当,缓解民企融资困难,积极为广大小微企业和民营企业创造更大的生存空间。要积极开展对广大民营企业和中小微企业的走访工作,认真梳理走访企业的共性问题,找准企业的融资痛点难点,通过推进企业在线融资,提升小微企业授信的专业化管理水平,创新小微企业金融服务,帮助企业拓宽融资渠道,扩大信贷工厂批量授信规模等方式,切实做到“对症下药”。

证明必要性。因为F是面向对象概念约简,所以F是面向对象概念协调集,有
又因为

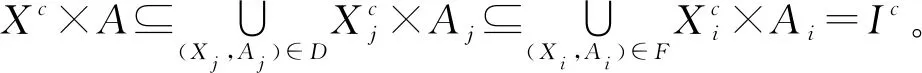
即F是面向对象概念协调集。

2.3 面向对象概念特征
依据面向对象概念在约简过程中所起的不同作用,可以把面向对象概念分为三类,具体如下。

例4(续例1)对于表1中的形式背景,其面向对象概念的分类见表3。

表3 形式背景K的面向对象概念分类
综上可知,给定一个形式背景,对于任意一个面向对象概念约简,它一定包含所有的核心面向对象概念,一定不包含不必要面向对象概念,并且包含部分相对必要面向对象概念。通过这些面向对象概念,最终可以重新构建给定形式背景的二元关系。
3 结论
本文研究如何在重构原形式背景二元关系的前提下进行面向对象概念的约简,并将面向对象概念分为核心、相对必要和不必要面向对象概念。文献[8]与文献[10]研究了在经典形式概念框架下的保持二元关系不变的因子分解与概念约简问题。虽然本文亦是研究概念约简,但二者存在着两点重要不同。其一,形式概念与面向对象概念具有不同的语义,适用于不同的应用场景。其二,对于同一个形式背景,形式概念与面向对象概念不存在直接的对应关系,不能互相诱导,这就造成了文献[10]中的结论无法直接推广到面向对象概念的约简。上述差异表明本文的研究不仅是有意义的,而且是很有必要的。
由于计算集合族的全体极小碰撞集是一个NP-hard问题,形式背景的规模及其关系的填充比例将直接影响概念约简的计算时间。因此,对形式背景与概念约简的计算时间两者关系的实验与理论研究也是十分有意义的。此外,众所周知,形式概念分析的研究已经不再局限于经典形式概念,因而如何将现有的概念约简研究拓展到面向属性概念[27]、三支概念[28]、近似概念[29]、模糊概念[30]也是值得深入探讨的问题。
(责任编辑:何军民)

