不规则场地土方量计算的对比研究

程亮 钟岩 刘继龙 赵延

摘 要：土方工程作为地基与基础工程中的重要施工环节，面对复杂的场地地形条件，如何高效、精确的进行土方工程量计算是亟待解决的问题。传统的土方量计算主要采用手工分区、分块后利用体积公式进行计算。对于复杂地形场地，手工计算工程量大，且后期修改困难。基于项目案例，介绍了运用Surfer进行不规则场地建模的方法和土方量计算的基本流程，对比分析了系统内置的各种建模方法，给出了系统内置插值方法的一般选用原则。根据数据集的差异化特点，从确立的数据分析目的出发，做到合理优选，灵活运用，并在此基础上得到精度可靠、符合实际的可视化模型。与传统计算程序HTCAD的土方量计算结果作了对比验证，为后期基坑工程土方工程量的计算分析提供方法参考。

关键词：基坑;地表建模;插值方法;土方量计算

Abstract： Earthwork is an important process in subsoil and foundation projects. Under complex conditions， it is an urgent task to efficiently and accurately calculate the volume of earthwork. Traditional earthwork calculation mainly adopts manual partitioning and calculation with volume formula after partitioning. For sites with complex surface， manual calculation requires a large amount of work and is difficult to modify. This paper introduces Surfer-based irregular site modeling and the basic process of volume calculation in earthwork， compares the various modeling methods， and presents the general selection principle of system built-in interpolation method. According to the differentiated characteristics of the data set and the established data analysis purpose， a reliable and realistic visualization model can be obtained through reasonable optimization and flexible application. Comparison is also conducted with the calculation results of the traditional calculation program HTCAD. The paper provides a reference for further earthwork calculation and analysis.

Keywords： excavation engineering; site surface modeling methods; earthwork volume calculation

土方工程作为地基与基础工程中的重要施工环节，需要对不同项目类型、不同场地要求、不同现状条件进行针对性的方案设计及施工组织。其中基于现场地形地貌的土方工程规划、土方工程量估算、成型后的土方工程量核算，都是重要的基礎性工作，尤其是面对复杂的场地地形条件，如何高效、精确的进行土方工程量计算是亟待解决的问题。

目前，传统的土方量计算主要采用手工分区、分块后利用体积公式进行计算，对于规则场地比较容易得出精确计算结果，但对于复杂场地地貌，适应性较差，且对于复杂地形条件场地，手工分块工程量大，修改困难（邱枫，2017）。为解决这一矛盾，目前已有一些土方计算软件如 HTCAD 和 CASS可以实现计算功能，但其模型主要考虑为二维模型，对复杂地形的适应还存在一定的困难和计算误差（闫晓敏，2019）。另外，一些学者基于ArcGIS运用栅格相减的计算方法进行土方工程量计算（黄俊杰等，2020），港口、航道、水利等多个工程领域的设计阶段，结合业务内容使用Civil 3D 进行深化及二次开发，也可以用做土方工程量的计算分析手段（赵丽等，2020）。

Surfer软件广泛应用于地质图件处理，土方量测算是其建模生成3D曲面后的一种典型应用。基本原理是利用已知三维空间的XYZ点值，创建一个基于网格的图形，用于后续建模或者计算分析（贺来国，2020）。Surfer软件中内置多种建模插值方法可供采用，但对于各种插值方法的适用性及对比研究还较少。

本文基于实际的项目案例，介绍了运用Surfer进行不规则场地建模的方法和土方量计算的基本流程，对比分析了系统内置的各种建模方法，给出了插值建模方法的一般选用原则，并与传统计算程序HTCAD的计算结果作了对比验证，为后期基坑工程土方工程量的计算分析提供方法参考。

1 项目基本情况

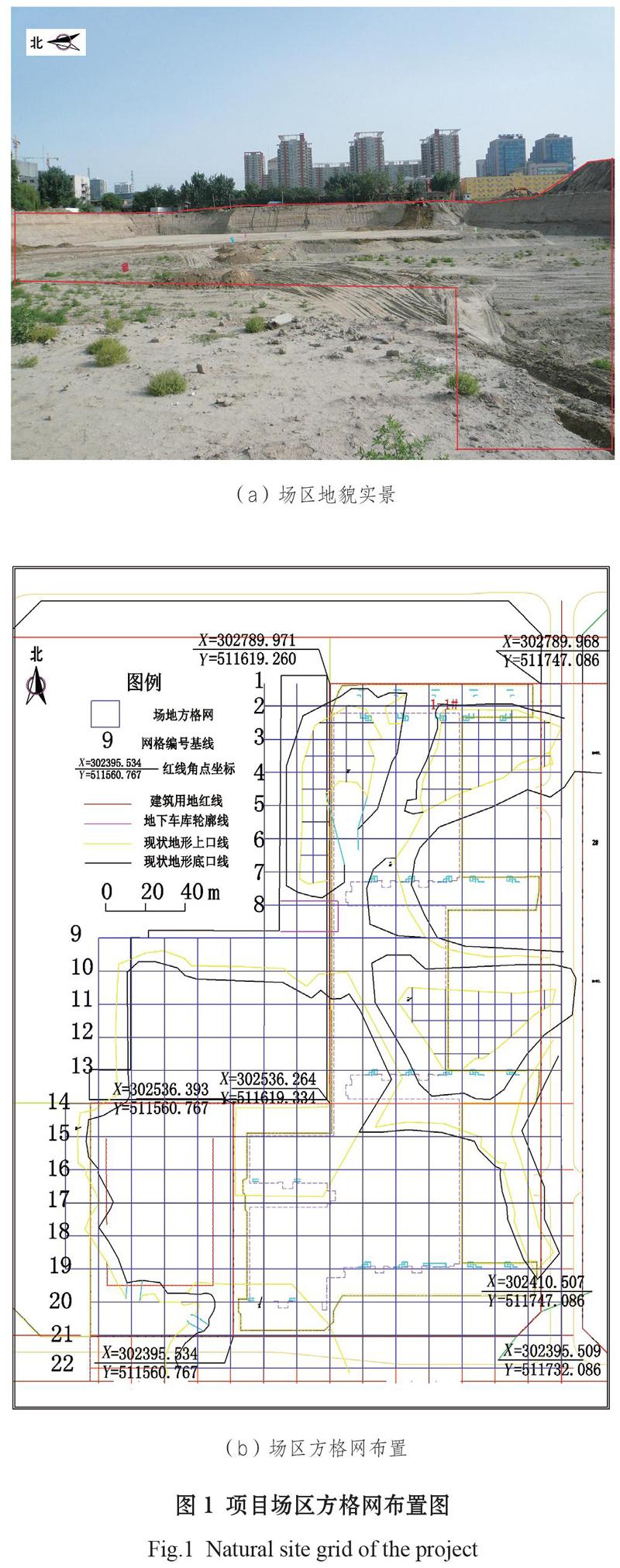
项目案例设计地下4层、基坑深度约19 m。项目进场施工前，建设单位已对表层污染土壤进行了土方治理。先期进行的大面积挖填方施工造成局部地区凹凸不平，且受人工取土、堆土等影响，地形高差较大，土方工程量的确定存在一定困难。

从场区地貌实景可看出（图1a），该场地地形高差较大，但界面边缘较为清晰，施工周界范围固定（62个点位，连接形成封闭边界）。前期工作已测得现场自然地貌方格网数据（284个点位，图1b）。

2 Surfer软件建模流程简介

Surfer系统内置的离散数据内插方法，几乎包括了目前常用的所有插值方法。默认的网格生成方法中有多种点内插方法，选择后可生成网格，然后再绘制所需的图形。之后设置基底曲面或高程，就能够计算出模型体积（白世彪等，2012）。

为了能够更好地为工程服务，必须熟悉各种系统内置的内插方法的基本原理，根据所面对数据的差异化特点，从项目伊始确立的数据分析目的出发，做到合理优选，灵活运用，对比差异，就能做出科学的选择。灵活地进行参数设置内插生成网格文件，在此基础上可以得到精度可靠、符合实际的可视化模型，供我们后续使用。

生成3D曲面模型后，可以查询计算模型的体积参数，求得土方工程量。软件计算所采用的数值计算规则有梯形法则、辛普森规则、辛普森（Simpson）3/8规则，这些方法都是数值积分的常用方法，适用于进行定积分计算。这3种方法本质上都属于牛顿-柯特斯求积公式（刘彬清等，2002）。它们以函数于等距n+1点的值，取得一个n次的多项式来近似原来的函数，再行求积。

取估算基准面基坑底平均标高Z=17.37 m，土方工程量计算结果见表1。

3 离散数据内插方法的对比研究

3.1 采用领域内平均值建模的方法

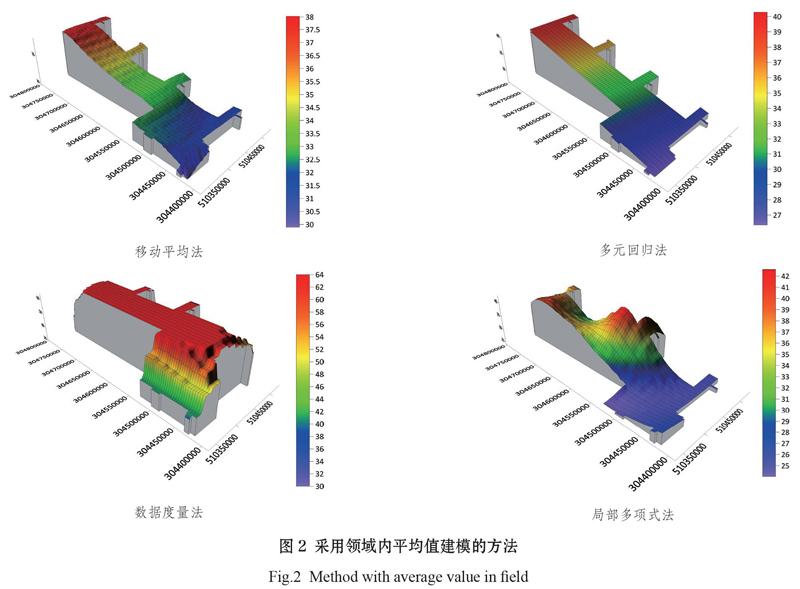
本类方法是分析模型中任意一点的周边的变化趋势分量，求其曲面内其他各点的空间位置，结合分布特点求平均所得，一般是圆形或方形区域，相当于对区域的趋势分析（李佳民，2019），主要有移动平均法、多元回归法、数据度量法等。根据各方法的理论特点及建模后图形（图2），可见：

（1）共性特征

以已知任意一点的周边的变化趋势，拟合圆形或方形区域曲面来进行建模，主要用来表征区域内趋势。较适用于场地较为平缓、场区内高差较小的项目建模。

（2）差异性特征

数据度量法从项目计算数据看，所得数据的偏差较大，不能直接用于工程。主要是用在建模初期，用来找到相对合适插值方法的一种手段。所得到的数据也可作为其他建模方法的输入，不是一种真正意义的插值算法。

移动平均法能够在一定程度上显示原始数据点的差异，但不能够明显的确定高差突变的周界，如果点位分布密度较低，且不均匀时，会出现较大范围内高程数据受到个别点位影响的情况，即扩大了原始数据点的影响范围。

多元回归法拟合形成的曲面平坦，不能够正确反映出局部的高程变化趋势，只是反映了整体上的场区分布，表示了场区的倾斜方向，可以用单独的多项式来近似拟合。

3.2 距离加权为主的插值方法

本类方法是以离散点附近局部区域内各点与离散点的平均加权距离为基准进行插值建模。主要有：反距离加权插值法（Shepard方法）、克里金插值法（空间自协方差最佳插值法）、最小曲率法、改进谢别德法等。根据各方法的理论特点及建模后图形可见图3。

（1）共性特征

均为平滑、精确的描绘曲面形态的方法，与领域内平均值建模的方法相比，已经能够比较明显的表示出场地高差的变化，对于本场地，拟合精度得到提升。但从形态上看，就本场地而言，高差差异较大，不能够很好反映界面的过渡，交界面过于平缓。

（2）差异性特征

克里金能够综合体现目标的形态、形状及其他空间特征，包含的信息容量更大，但为了达到无偏线性估计，且能得到最小方差，必须对每个目标指定系数（洪成晶，2020）。最小曲率法为了得到尽可能平滑的曲面，会牺牲一定程度的精确度。改进谢别德法当增加、删除或改变一个点的特征时，使用距离倒数加权的最小二乘方的方法，无需频繁计算权函数。

3.3 采用临近点位建模的方法

临近点位建模方法是将模型看成泰森多边型的集合，当需要在模型中插入数据进行加密时，修改多边型参数，使用相邻点位的权重均值作为比例基准进行插值建模。主要有：自然邻点插值法、最近邻点插值法、径向基函数插值法、三角网-线性插值法等（图4）。

（1）共性特征

本类模型可以允许界面存在较大差异，而非完全光滑曲面。为满足精度要求，多边型的大小以收缩为主，以满足精度要求。与距离加权为主的插值方法相比，已经能够比较明显的表征出界面差异的存在，各组计算数据的差异。

（2）差异性特征

自然邻点插值法中关注点的权重是重要决定因素，目标多边型的尺寸差异，多边型均减小大小，在数据点凸起的位置并不外推等值线。

最近邻点插值的隐含的假设条件是任意网格点的属性值都使用距它最近的位置点的属性值，用每一个网格节点的最近邻点值作为待求的节点值。结合现场场地特征，该方法与现场的现状最为相似，工程实践中采用了最近邻点插值法的计算数据。

径向基函数一般是由单变量函数构成。径向基函数方法下生成的光滑曲线，曲面适应数据的能力较好.能够根据数据情况，得到适宜的拟合结果，也可以根据需要，引入圆滑系数，将曲面变得更加平滑。

三角网-线性插值法是使用最佳的三角形来描述网格各节点对应的网格面，网格面的倾斜程度和高差分布都由定义网格面的周边3个原始数据点位确定，是一种典型的线性插值方法。

3.4 与HTCAD的计算结果对比分析

HTCAD是基于AUTOCAD 平台开发的专业土方计算地形分析软件（陈家华等，2020），通过原始数据点采集或设置，设计高程点布置及设置，划分场区和网格，计算自然地形和设计高程的方式，汇总得到土方工程量。根据土方挖填量的结果可进行分区域调配优化，给出土方平衡解决方案。

工程选用了15 m和10 m网格的划分方法，分别采用四方棱柱、三角棱柱体积计算公式进行计算，结果与Surfer计算成果对比见表2。

根据计算结果及实际计算过程对比可知：1）HTCAD 和Surfer軟件的计算结果差异7%左右，HTCAD略偏大，属于合理计算误差范围;2）Surfer建模成果的可视化效果明显优于HTCAD，能够直观的进行模型适用性判断，而HTCAD 土方计算汇总需要严格按照既定步骤进行，且网格文件生成后重新修改较为繁琐;3）Surfer软件的建模、修改简便，系统内置建模方法较多，建模速度快，而HTCAD 只能基于四方棱柱、三角棱柱的体积公式进行计算，存在一定的局限性。

4 工程实践中模型选择的建议

（1）方案选择

方案初选时，可以优选领域内平均值建模的方法，如移动平均法、多元回归法、数据度量法等，该方法可以大体上确定拟合模型的表面特征和分布规律，由于忽略了一些数据细部的变化趨势，对于大数据量的建模较为迅速，能够反映整体趋势。

初步确定方案后，可以根据地形、地貌的分布特征，有选择的进行对比分析，根据各拟合方法特征，找到更加能够还原现场实际的建模方法。如果模型有比较明显的切断情况，可以优选三角网-线性插值法，它能够比较明显的显示这种关系。

（2）原始数据的稳定

反距离加权插值法或克里金插值法的优势在于原有数据点值在插值过程中不做修改，原有数据点就是模型形成后的数据点，能够最大程度保留点位原有数据。

（3）利用等值线图

面对大量数据，可以先选择小的数据样本用来生成测试网格，之后可以绘制等值线图，作为插值模型选型的辅助依据，更为高效。结合现场采样时的地表、地貌特征，综合判断选择合适的插值方法后再进行整体建模。

5 结论

最近邻点插值方法能够高契合度表现场地特征，实际的工程实践中各参建单位也采纳了最近邻点插值法的计算数据。

基于Surfer的土方工程量计算的方法差异及点位布置情况可见，前期建模的重点是选择合适的建模方法，要根据客观环境特征及所取得的数据集特点及分布规律，特别是考虑采样数据集总量及采样网格规则程度这两个特征指标，选择最适宜的网格化算法，在充分考虑模型特性的基础上，做出相对应的设置调整，以更契合现场地形实际。

适宜建模方法的选择能显著提高后期设计、施工及土方工程核算的质量，更好地为工程实践服务。

参考文献：

白世彪，王建，常直杨，2012. Surfer 10地学计算机制图[M]. 北京： 科学出版社.

陈家华，洪友堂，2020. 基于实测散点数据的规则格网法土方量计算与精度分析[J]. 北京测绘，34（10）：1417-1422.

贺来国，2020. 倾斜摄影技术在土方量计算中的应用研究[C]//中国图学学会建筑信息模型（BIM）专业委员会.第六届全国BIM学术会议论文集.中国建筑工业出版社数字出版中心：7.

黄俊杰，陈威，乔胜，2020. ArcGIS在生态清淤工程量计算的应用研究[J]. 山东化工，49（19）：235-237.

洪成晶，2020. 基于Kriging模型的工程土方量计算方法分析[J]. 四川建筑，40（6）：294-296.

李佳民，2019. 基于简单移动平均法的汽车售后配件需求预测研究[J]. 中国商论（14）：234-235.

刘彬清，任亚娣，2002. Newton-Cotes数值求积公式的渐近性[J]. 上海大学学报（自然科学版） （6）：503-506.

邱枫，2017. 土方工程量测算方法浅析[J]. 云南化工，44（7）：67-69.

闫晓敏，2019. Civil 3D在港区工程量计算中的应用[J]. 海岸工程，38（2）：115-123.

赵丽，孔庄，2020. Civil 3D在水系综合治理工程中的应用分析[J]. 港工技术，57（6）：85-87.