装配式连续梁桥计算方法的比较分析

叶 佳 张伟山

（湖北交投智能检测股份有限公司， 湖北 武汉 430000）

0 引言

近年来，装配式连续梁桥由于结构形式简单，工厂预制标准高，施工方便，节约材料的特点，被广泛采用在我国中小跨径桥梁建设中，这使得装配式连续梁桥在试验检测工作中占比很大。针对装配式连续梁桥的横向分布系数计算，一般按照简支梁状态下荷载横向分布理论进行计算；然而，按照简支梁状态下的荷载横向分布理论来进行连续梁的结构验算是否合适是值得思考的。

本文采用刚性横梁法、修正刚性横梁法、梁格法和实体单元法4 种方法对装配式连续梁进行结构计算并结合桥梁静载试验测试数据，对比分析了装配式连续梁的横向分布特性，为试验检测工作中更客观评价装配式连续梁桥的结构性能提供参考。

1 计算原理

目前，对于装配式连续梁桥较为常用的计算方法主要有荷载横向分布计算理论、梁格法、实体单元法。本节仅对荷载横向分布计算理论和梁格法作简要介绍：

1.1 荷载横向分布计算理论

常用的荷载横向分布系数计算方法主要有：杠杆原理法、偏心压力法、横向铰接板法、刚性横梁法、比拟正交异性板法[1-3]。上述方法都是按照简支梁结构形式来进行荷载横向分布系数求解的。对于先简支后连续结构[2]，基于等效刚度换算实现了连续梁桥荷载横向分布系数计算的修正；即假设连续梁各跨截面相同，抗弯惯性矩均为 ，根据挠度等效原理换算后的简支梁截面抗弯惯性矩为 。刚度换算表达式为：

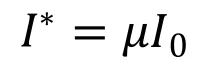
式中：μ 为等效刚度换算系数。

1.2 梁格理论

梁格法的核心是利用等效纵、横梁格代替桥梁上部结构，将分散在梁上的弯曲刚度、抗扭刚度集中在最邻近的等效梁格内，即纵向刚度集中在纵向梁格内，横向刚度集中在横向梁格内。理想的刚度等效原则是：上部实际结构和对应的等效梁格所承受的荷载相同时，两者挠度相等，并且每一梁格内的弯矩、剪力和扭矩都等于该梁格所代表的部分上部结构的内力[4-5]。梁格法的关键在于通过合理的梁格网格划分和横向联系刚度取值来准确模拟实际结构。

本文采用传统的刚性横梁法来进行静载试验过程中的结构计算，并与基于等效刚度换算的修正刚性横梁法[3]、梁格法、实体单元法进行比较，结合静载试验实测数据进行了分析比较。

2 工程概况

以4×40m 先简支后结构连续预制小箱梁作为研究对象，箱梁梁高2m，顶板厚19cm，腹板厚20cm，底板厚18cm，横向布置5 片小箱梁，桥面净宽15.75m，设置端、中横隔板。

对于装配式连续梁桥的静载试验，一般选取受力最不利梁作为试验加载对象；本文仅对同时受力最大的1#梁和2#梁的主跨跨中截面进行试验研究，测试主梁应变和挠度两个力学指标。截面测点布置图如图1所示：

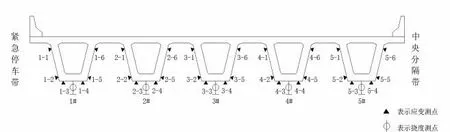
图1 测点布置图

3 结果分析

3.1 挠度分析

静载试验和不同计算方法下主梁挠度对比如表1 和图2 所示。

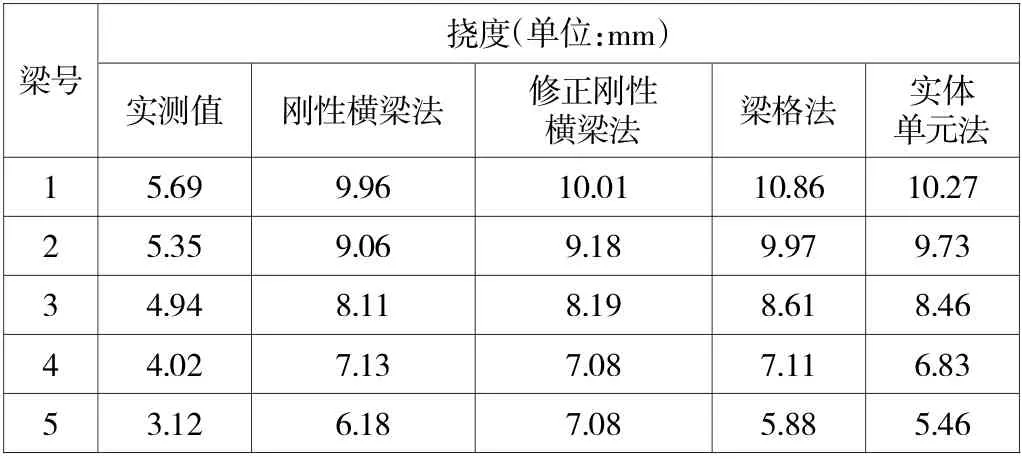
表1 主梁挠度计算结果对比表

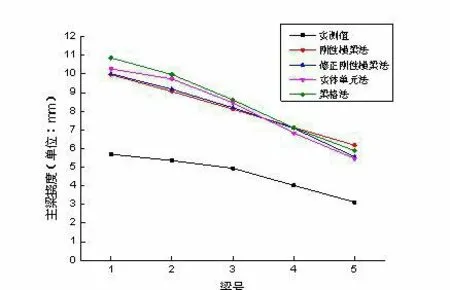
图2 主梁挠度分布曲线

由表1 和图2 可知：不同计算方法下，主梁挠度由大到小依次为梁格法＞实体单位法＞修正刚性横梁法＞刚性横梁法；采用刚性横梁法计算得到的挠度校验系数最大，采用梁格法计算得到的挠度校验系数最小。以受力最不利的1#梁为例，修正刚性横梁法较刚性横梁法计算得到的挠度增大了0.5%，实体单元法较刚性横梁法计算得到的挠度增大了3.11%，梁格法较刚性横梁法计算得到的挠度增大了9.04%。刚性横梁法、修正刚性横梁法、实体单元法3 种计算方法对挠度计算误差保持5%以内，应用于静载试验结构挠度计算中能有效保证计算精度。

3.2 应变分析

试验荷载作用下，1#梁各应变测点实测应变值与理论应变值见图3。各片主梁底板应变如图4 所示。

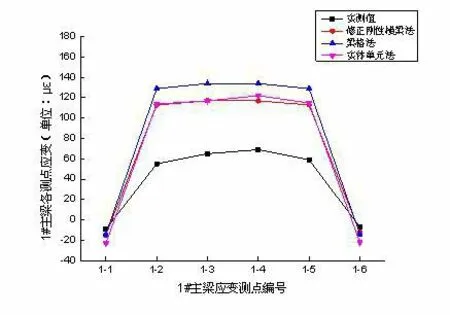
图3 1 号梁应变分布曲线

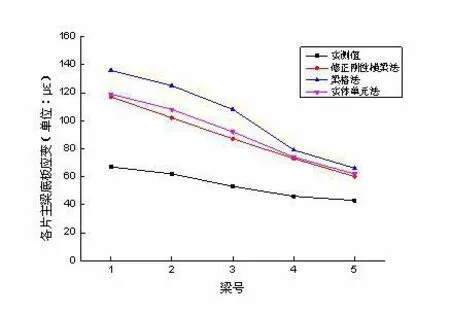
图4 主梁底板应变分布曲线

由图3 和图4 可知：不同计算方法下，主梁应变变化趋势基本保持一致，主梁理论应变由大到小依次为梁格法＞实体单位法＞修正刚性横梁法。修正刚性横梁法和实体单元法计算得到的理论应变较为接近，且均小于梁格法计算得到的理论应变值，采用修正刚性横梁法或实体单元法进行应变理论值计算能得到更大的应变校验系数，对评定桥梁承载能力更为严格。

梁格法或实体单元法计算出的1#梁～2#梁底板应变曲线斜率与实测1#梁～2#梁底板应变曲线斜率较为吻合，且比修正刚性横梁法计算出的1#梁～2#梁底板应变曲线斜率更为平缓，这反映出了中梁（2#梁）能替边梁（1#梁）分担一部分内力的规律；因此，在静载试验加载实施中，应更多关注2#梁承担荷载的风险。

3.3 横向分布系数分析

荷载横向分布系数可以通过各主梁挠度来直观反映；本文根据主梁挠度确定各主梁的横向分布系数。

主梁实测横向分布系数与不同计算方法所计算的横向分布系数比较如图5 所示。

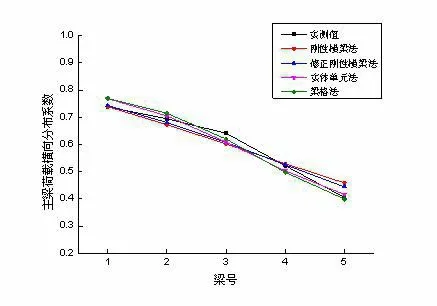
图5 主梁横向分布系数

由图5 可知，采用刚性横梁法计算得到的各片主梁横向分布系数要略大于采用修正刚性横梁法计算得到的横向分布系数；采用梁格法计算得到的各片主梁横向分布系数最大；采用实体单元法计算得到的各片主梁横向分布系数曲线变化规律与梁格法较吻合，计算值介于修正刚性横梁法计算值与梁格法计算值之间。

对于受力最不利控制梁而言，边梁（1#梁）实测横向分布系数实测值要小于各类方法得到的计算值，中梁（2#梁）横向布系数实测值介于修正刚性横梁法计算值与实体单元法计算值之间，且1#梁～2#梁横向分布系数曲线斜率较任何一种方法计算得到的横向分布系数曲线斜率都要平缓；这进一步说明了该桥横向刚度较大，2#梁能替1#梁分担一部分内力。

4 结束语

（1）对于装配式连续梁的计算，采用修正刚性横梁法或实体单元法计算精度较高。梁格法计算出的挠度、应变以及荷载横向分布系数结果均偏大，采用偏大的荷载横向分布系数进行加载计算时会造成试验荷载偏大，不利于结构安全；采用偏大的挠度、应变理论值计算结构校验系数时会造成校验系数偏小，不利于客观的评定桥梁的承载能力。

（2）中梁（2#梁）能在一定程度上分配边梁（1#梁）的内力，造成边梁（1#梁）最不利受力工况下，中梁（2#梁）内力分配较大的情况；因此，进行边梁（1#梁）最不利受力工况荷载加载时，也要关注中梁的试验控制参数指标。