基于多层联合降噪的信号处理方法

徐信芯， 姜 鑫， 张 辉， 高康平， 尚晓飞

(1.长安大学工程机械系公路养护装备国家工程实验室， 西安 710064； 2.河南省高远公路养护技术有限公司, 新乡 453003)

在旋挖钻机钻进过程中，钻头的振动信号承载了井下钻遇地质体的特征信息，可以综合反映井底的钻进工况[1]。目前，基于钻头信号监测的系统能够有效获取井下工况信息，但钻井施工环境复杂多变，使得传感器采集到的钻头振动信号具有变量多、大数据融合、部分数据随机扰动以及分析处理复杂等特点[1]。因此，为了更好地提高破岩效率和钻头使用寿命，需要对现场采集的信号进行降噪处理。

振动信号具有非线性、非平稳的特点，这类信号重点在于获得其时域局部性质。在处理此类机械振动信号时，常用分析法有3种，相比于时域、频域分析法，时频分析方法得到了广泛应用，如经验模态分解 (empirical mode decomposition，EMD)[2]。利用EMD方法，可以在无需人为挑选基函数的情况下，将振动信号自适应地分解，得到若干频率由高到低的固有模态函数(intrinsic mode functions，IMF)，并通过挑选需要的IMF，实现特定滤波[3]。但EMD分解会出现模态混叠，且还存在过包络与欠包络问题[4]。文献[5]研究表明，LMD算法相对于EMD算法具有更强的信号分解能力与时频特征分析能力[6]；对比一般的时频分析方法，LMD则不需要考虑信号的平稳性，不但可以将非平稳信号自适应分解为若干PF分量，而且解决了EMD算法的过包络、欠包络等问题，因此，在振动信号降噪领域取得了广泛应用[7]；然而，LMD 分解过程仍存在一定程度的模态混叠问题。文献[8]通过小波变换(wavelet threshold，WT)抑制了噪声干扰，并通过 Hilbert 变换解调了故障特征频率，以此证明了小波降噪与 Hilbert 变换组合能够在电机振动信号处理中应用。小波阈值降噪(wavelet threshold denoising，WTD)是一种有效且强大的算法，研究方向也从一组数据或信号中去除噪声转化为在数据系中找到最佳阈值，专家与学者们都针对小波变换提出了很多的阈值方法[9]。在信号处理方面，奇异值分解(singular value decomposition，SVD)方法主要用于信号降噪和周期成分提取，奇异值分解后选取合适的阈值重构信号，能够有效地保留有用信息，并消除原始信号中的噪声干扰[10]。

基于此，现针对钻机试验台钻杆振动信号具有非线性、非平稳以及多源振动耦合的特点，采用LMD、WTD、SVD三种理论，提出一种多层联合信号降噪方法，对振动信号进行降噪处理，提高信噪比，达到提取有效信号的目的，最终实现信号去噪。

1 基本理论

1.1 局部均值分解

LMD是将目标信号的局部极值点进行循环迭代，从原始序列中分离出纯调频信号与包络信号，将其进行乘积后便可得到一系列由高频到低频的PF分量[7]。文献[11-14]展示了原始信号x(t)的分解方法，过程如下。

步骤一找出原始信号x(t)的所有极值点，按照式(1)求出其所有相邻的ni、ni+1的均值，并用3次样条曲线将所有均值点mi依次连接起来，平滑处理分段函数，获得局部均值函数m11(t)。

(1)

步骤二利用极值点ni，按照式(2)计算出所有相邻极大值、极小值点的包络值ai，采用上述方法就可以得到包络估计函数a11(t)。

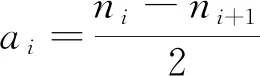
(2)

步骤三按照式(3)从原始信号x(t)中分离出函数m11(t)，得到h11(t)函数；利用式(4)用a11(t)对h11(t)进行解调处理，得到调频信号s11(t)。

h11(t)=x(t)-m11(t)

(3)

(4)

步骤四判断s11(t)是否为纯调频信号的标准为包络函数满足a12(t)=1，相反，就需要把s11(t)作为原始信号重复步骤一～步骤三，直到s1n(t)为纯调频信号，迭代终止。但在应用中，包络估计函数不可能完全为1，只要符合|1-a1n|≤δ(δ为变量)，停止迭代。过程如式(5)、式(6)所示。

(5)

(6)

步骤五把步骤四迭代过程中产生的所有包络函数按照式(7)相乘得到包络信号a1(t)为

a1(t)=a11(t)a12(t)a13(t)…a1n(t)=

(7)

步骤六将纯调频信号s1n(t)，用包络信号a1(t)按照式(8)进行调幅，可得到第一个调频-调幅的PF分量为

PF1(t)=a1(t)s1n(t)

(8)

步骤七PF1(t)包含了原始信号x(t)中最高频成分，按照式(9)，计算出包络信号的瞬时频率f1(t)为

(9)

步骤八将PF1分量从给定信号x(t)中分离出来，得到新信号u1(t)，按以上步骤一～步骤七再将此新信号进k行次循环迭代，直至最后得到的信号uk(t)为单调函数，停止迭代。迭代过程如式(12)所示。

(12)

最终原始信号x(t)被分解为所有PF分量与uk(t)之和，如式(13)所示。

(13)

式(13)中：PFj(t)为单个调频-调幅信号；uk(t)为剩余单调函数。

1.2 小波阈值降噪

小波变换广泛应用在故障诊断和噪声滤除方面，它是把原始信号与基小波函数按照式(14)经过平移和尺度变换后做内积。在进行诊断时，通常需要同时从时域和频域进行分析，小波变换正好能满足这些需求，还能很好地适用于非平稳信号[10]。小波阈值降噪便是基于小波变换的一种信号降噪方法，是小波变换的重要应用之一。

(14)

式(14)中：a为尺度参数；b为位置参数；t为时间；Ψ(t)为共轭小波基。根据钻机试验台振动信号的特征，选择紧支集正交小波(daubechies，db)小波。

(15)

(16)

1.3 奇异值分解

1.3.1 SVD降噪原理

奇异值分解是分解矩阵的一种方法，可以按照式(17)将维数为m×n的矩阵Hm×n分解，得到如下形式。

(17)

式(17)中：Dm×n和Vm×n为正定矩阵；Σm×n为1个非负对角矩阵。Σm×n对角线元素σ1,σ2,…，σi[i=min(m,n)]即为Hm×n矩阵奇异值(秩为i)，且满足σ1≥σ2≥σ3≥…≥σi[16]。奇异值包括了分解前矩阵的全部信息，通过对奇异值的处理，分析原始数据，能够实现预期的需求。针对一维时域数据，奇异值降噪原理如下。

按照式(18)，通过相空间重构，将含噪信号X(N)={x1,x2,x3，…，xN}转换为Hm×n矩阵。

(18)

式(18)中：N=m+n-1；Dm×n为含噪信号的有效成分子空间；Wm×n为噪声成分子空间。基于式(18)，按照式(17)进行奇异值分解。

1.3.2 Hankel矩阵维数和有效阶数的确定

(19)

n=N+1-M

(20)

SVD降噪是一种非线性滤波方法，具有良好的稳定性和不变性，被广泛地应用于信号滤噪、特征提取以及故障诊断[10]。确定重构矩阵阶数尤为重要，有效秩阶数K太大，会引入噪声干扰，降噪效果变差；秩太小，则会导致故障信息丢失；因此，选择适当的奇异值有效秩阶数，就能够高效的去除噪声以及提取有效信号。针对SVD分解这一关键技术，基于文献[17]，按照式(21)来确定奇异值的有效阶数K[18]，公式为

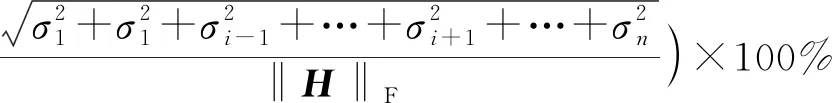
(21)

式(21)中：PCTEσi为加权能量贡献率；‖H‖F为矩阵Hm×n的范数。

2 LMD-WTD-SVD联合降噪处理

针对EMD、 LMD及其改进算法存在模态混叠问题，人为挑选PF分量致使部分有效信号遗失、噪声滤除不干净这一问题，并结合 LMD 的自适应性、WTD在高频分量分辨率较高的特点以及SVD在提取信号周期成分和滤除随机噪声上的优良特性，提出了基于LMD-WTD-SVD的信号降噪方案[19]。

2.1 PF分量的挑选

对EMD与LMD分解后信号分量进行挑选，一般采用K-L散度法(Kullback-Leibler divergence，K-L divergence)和相关系数(correlation coefficient, CC)法，达到有效去除噪声成分、保留有效成分的目的[2]。结合振动信号分解需求及分量选取的应用，着重考虑到适用性问题，选择了PF分量与原始信号的相关系数法作为LMD分解后PF分量筛选的依据[20]。相关系数计算如式(22)所示。

(22)

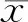
2.2 多层联合降噪处理过程

在获得相关系数后，针对上述人为挑选PF分量所存在的问题，设计提出了LMD-WTD-SVD多层联合降噪处理方法，算法流程图如图1所示，具体步骤如下。

步骤一输入含噪声信号，进行LMD分解，获得各个 PF分量。

步骤二计算相关系数。

步骤三依据相关系数，对PF分量进行筛选，并将剩余分量舍去。

步骤四对选取的有效分量分别进行WTD降噪，并进行信号重构。

步骤五对步骤四的结果按照第2节中的方式进行SVD降噪。

步骤六将步骤五获得的重构信号与步骤三中的残余PF分量进行叠加，获得LMD-WTD-SVD最终降噪结果。

3 仿真分析

为验证联合降噪方法的合理性和有效性，引入含有高斯白噪声的调频-调幅信号进行MATIAB仿真实验。其中，原始信号x(t)=sin(2π·50t)+sin(2π·30t)，采样频率设置为1 024 Hz，采样长度为1 024。原始信号波形图如图2所示，加入高斯白噪声的含噪信号的波形图与频谱图如图3(a)、图3(b)所示。

对含噪信号进行 LMD 分解得到5个PF分量的波形图和频谱图如图4(a)、图4(b)所示，每个PF分量所对应的相关系数指标结果如表1所示。

PF1、PF2、PF3分量的相关系数远大于其他PF值，其包含的噪声信号成分最多，有效信息成分也多，需要保留；相反，PF4、PF5的相关系数较低，予以舍去。将前3个分量进行重构，得到了第一次降噪信号；然后对PF1、PF2、PF3分别进行WTD小波四层软阈值降噪并重组,得到第二次降噪信号的波形图与频谱图如图5(a)、图5(b)所示。

图1 基于LMD-WTD-SVD的信号降噪流程图Fig.1 Signal denoising flow chart based on LMD-WTD-SVD

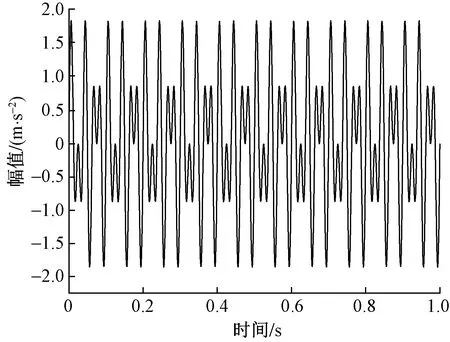
图2 原始信号波形图Fig.2 Original signal waveform diagram

图3 含噪信号的波形图与频谱图Fig.3 Waveform and spectral diagram of signal with noise

表1 各PF分量的相关系数值

最后对上述降噪结果进行SVD分解降噪，得到了LMD-WTD-SVD联合降噪信号，波形图与频谱图如图6所示；图6(a)中，能明显看出时域波形里的噪声得大大削减，波形与原始信号波形相近。图6(b)中，大量干扰频率已被去除，有2个主要频率，降噪效果明显。

采用EMD-SVD、LMD-SVD两种典型方法做了比对验证，结果如图7、图8所示。其中，EMD-SVD降噪结果如图7(a)、图7(b)所示，波形图中噪声干扰还较严重，噪声频率还未得到有效滤除。LMD-SVD降噪方如图8(a)、图8(b)所示，降噪效果强于前者，但降噪信号中仍然含有少量噪声成分。相比于此，所提方法明显优于其他两种方法。

为进一步说明降噪效果，引入信噪比公式[式(21)]作为另一分析指标，得出了表2的EMD-SVD、LMD-SVD、LMD-WTD、LMD-WTD-SVD的信噪比。相比可以看出，后者能提高信噪比。综上，LMD-WTD-SVD算法能够有效滤除随机噪声，突显频率特征，是一种更优的降噪处理方法。

(21)

图4 含噪信号LMD分解结果Fig.4 Decomposition result of LMD of signal with noise

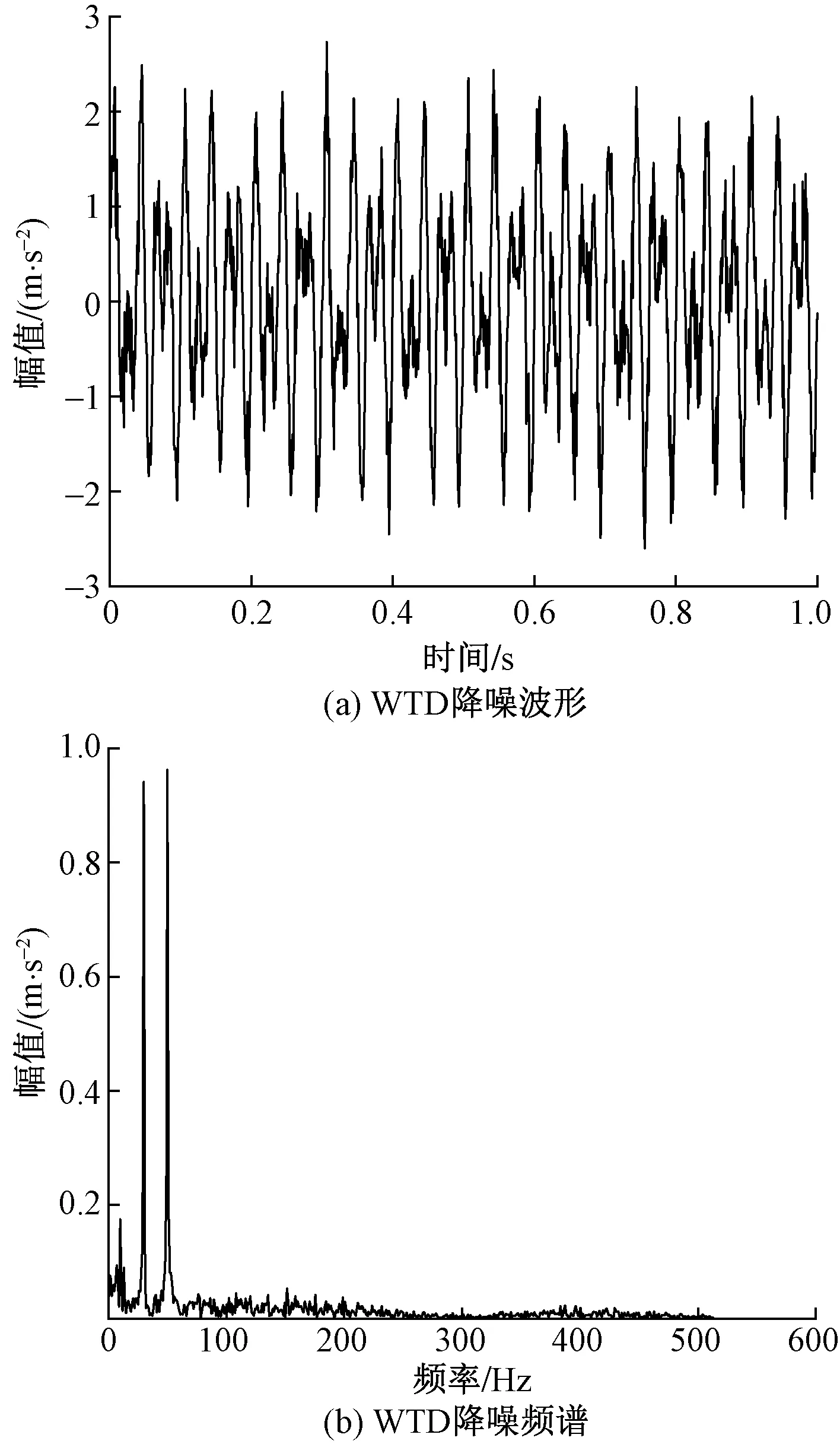
图5 WTD降噪结果Fig.5 WTD denoising results

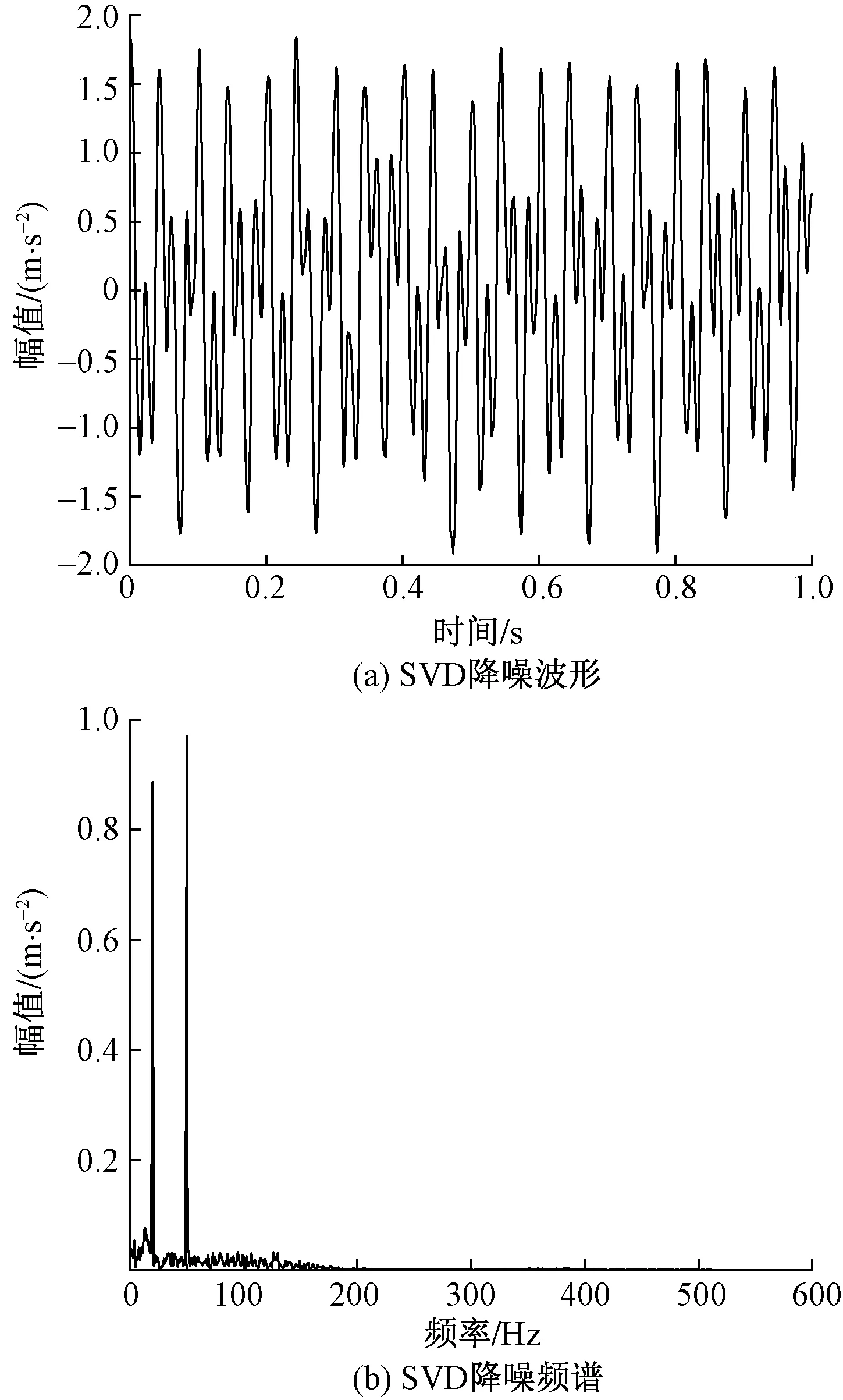
图6 SVD降噪结果Fig.6 Result of SVD denoising

图7 EMD-SVD降噪结果Fig.7 Result of EMD-SVD denoising

图8 LMD-SVD降噪结果Fig.8 Result of LMD-SVD denoising

表2 降噪效果对比分析

式(21)中：x(t)为原始输入信号；x(t)′为降噪信号；N为采样点数。在MATLAB仿真试验中，在原始信号未受噪声干扰的情况下，信噪比越大，表明信号中的噪声成分越少。

4 应用实验

为证明LMD-WTD-SVD多层联合降噪方法在信号检测中的适用性和优越性，采用了美国凯斯西储大学实验室轴承模拟数据进行验证实验。实验设备如图9所示，由编码器/扭矩传感器、功率测试计、电机及电子控制器等构成。采用SKF6205-2RS深沟球轴承，电机转速为1 750 r/min，电机功率1.5 kW，采样频率12 kHz，采样个数为2 000[21]。

为简洁地展示降噪处理效果，选取内圈故障的轴承的实验数据进行处理。降噪处理前后轴承数据的时域波形图和频谱图，分别如图10(a)、图10(b)和图11(a)、图11(b)所示。由图10可知，轴承数据中存在故障振动噪声，对后期的故障诊断和信号提取造成干扰。经过LMD-WTD-SVD联合降噪处理后，由频谱图可知，很好地保留了有效信号成分，过滤掉了高频振动噪声，达到了降噪的目的。

图9 试验系统Fig.9 Test system

图10 采样信号Fig.10 Sampling signal

图11 LMD-WTD-SVD联合降噪Fig.11 LMD-WTD-SVD combined noise reduction

5 结论

(1)充分发挥LMD分解的优点，利用相关系数挑选出有效PF分量并重构，得到第一次降噪信号，再结合SVD方法进行二次降噪，最后经过四层小波软阈值对其WTD降噪，并与其余PF分量进行重构，得到了LMD-WTD-SVD联合降噪信号。

(2)通过MATLAB做了EMD-SVD、LMD-SVD对比仿真实验，LMD-WTD-SVD能够更好地滤除振动信号中的噪声，是一种更优降噪方法。

(3)采用新提出的降噪方法，对开源轴承数据进行处理时，既能很好地滤除信号中的高频噪声成分，又不会造成信号成分缺失以及时域波形失真，能够准确、有效地用于轴承振动信号的降噪处理。