渤海高地饱压差油藏考虑应力敏感的产能评价方法
张占华,李 壮,蔡 晖,程林松,贾 品*
1. 中海石油(中国)有限公司 天津分公司渤海石油研究院,天津 300452;
2. 中国石油大学(北京)石油工程学院,北京 102249
针对应力敏感性油藏,国内学者已进行了许多研究。岩心的渗透率与孔隙度会随有效应力的增加而降低,并且在卸压后,岩心的孔隙度与渗透率无法恢复至初始状态,其存在一个永久性的损失(刘建军和刘先贵,2001; Jose and Chen,1997)。也正是因为这一特性,存在应力敏感的储层其产能在开发过程中会受到不可逆的伤害;低渗岩心的渗透率、孔隙度与有效应力间存在指数关系,即随着有效应力的增大,岩心的渗透率和孔隙度呈指数递减,但不同岩心需要通过实验测定相应的应力敏感系数(张新红和秦积舜,2001; Jones and Owens,1980);秦积舜通过增加岩心围压,使岩心的孔隙结构与骨架结构发生变化,根据其变化规律提出了一种新的表征围压—渗透率关系的指数函数线性组合(秦积舜,2003)。
针对储层应力敏感对产能造成的损害,国内已有相应研究。初始渗透率越低的岩心应力敏感性越强,固液耦合作用越明显,其渗透率损失越大,设定合理的储层产能界限应考虑到固液耦合的影响(王秀娟等,2003; Sudirman and Lewis,1994)。不仅低渗透储层具有应力敏感特征,异常高压中高渗油藏同样具有压敏现象,其会对岩心渗透率造成不可逆损失,且渗透率的恢复情况与渗透率呈对数关系,因此在油藏产能分析过程中应考虑应力敏感的影响(王永凯和李炼民,2019)。
Q油田W组油藏为层状构造油藏,沉积相类型主要是辫状河三角洲前缘—前三角洲亚相沉积,可划分出水下分流河道、水下分流间湾、河口坝、席状砂、远砂坝和前三角洲6种沉积微相。储层孔隙度以中孔为主,平均孔隙度为20%左右,渗透率变化范围较大,为25~380 mD,总体以中渗为主,各井区状况不同,部分井所在储层为低渗透。压力系数1.01,温度梯度3.26 ℃/100 m,原始地层压力24.3 MPa,饱和压力9.29 MPa,高地饱压差的特点使得应力敏感的影响增大,成为油藏开发中产能预测的关键因素。目前对于低渗特低渗油藏,考虑应力敏感的产能研究较为普遍(李小益和刘德华,2016;罗川,2019),但对于渤海高地饱压差油藏此类中高渗油藏的研究相对较少,且研究多为油藏形成机理方面(王永凯和李炼民,2019;盛军,2018;Geertsma,1957),对于如何针对应力敏感进行产能分析及合理开发调整的研究较少(丁景辰,2017;张赫,2019),因此应开展实验求得应力敏感规律,分析其对于产能的影响情况,为后期油田的开发提供指导依据。
1 目标区应力敏感特征及定量表征
1.1 目标区岩心资料
实验选取了Q油田Q2井、Q3井与Q5井的8块岩样进行气测渗透率实验,9块岩样的气测渗透率范围均在20~300 mD,孔隙度为20%左右(表1)。
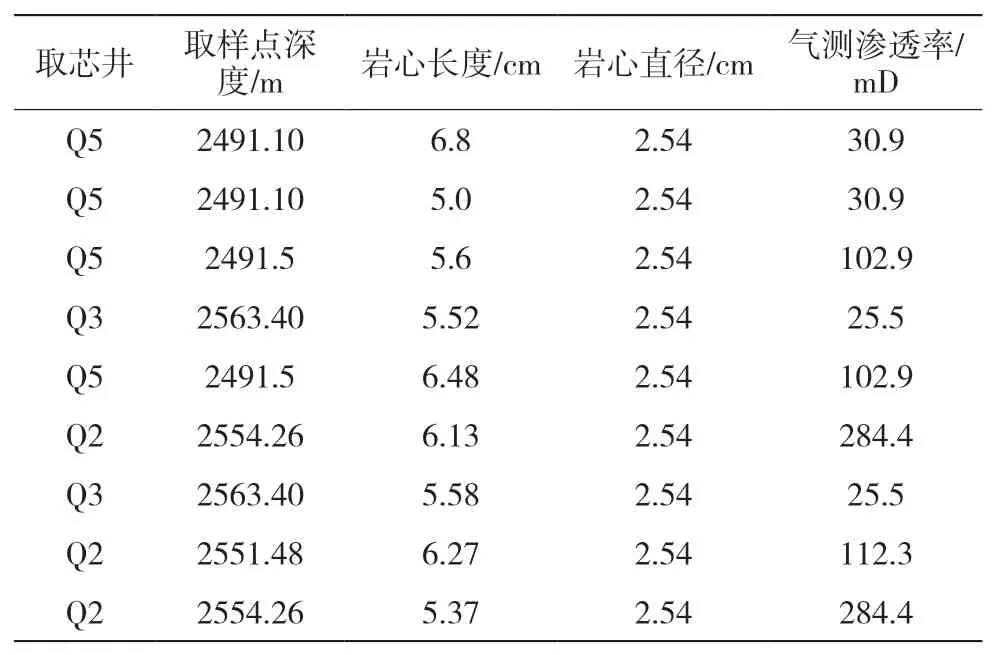
表1 取样岩心基本参数Table 1 Basic parameters of sampled cores
1.2 气测渗透率实验
将9块进行洗油处理后,干燥后进行气测渗透率实验,参照中华人民共和国石油天然气行业标准《SY/T5358-2010储层敏感性流动实验评价方法》设计实验(油气田开发专业标准化委员会,2010)。
在岩心夹持器中放入测量岩心,采用气测渗透率方法,驱动压力定为2 MPa。待气体流量计读数平稳后,通过围压泵改变岩心所受有效应力,来模拟地层应力敏感环境。升压过程中不断增大围压,变化量为2 MPa,记录流量计读数,围压升至50 MPa后停止,之后进入降压过程,仍然保持2 MPa变化量,记录气体流量计读数,分别对9块岩心重复进行三次升降压过程,记录实验数据。
1.3 渤海高地饱压差油藏储层应力敏感定量表征公式
通过对实验结果的分析处理,发现Q油田的应力敏感特性最为符合乘幂式关系(罗瑞兰,2006)。实验中,岩样所受有效应力为围压与驱替压力的差,即:
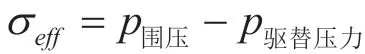
式中σeff:岩石所受有效应力,MPa;
岩样渗透率随岩石所受有效应力的增大而发生改变,求出每个时刻当前岩样渗透率与其初始渗透率的比值和与之对应的当前有效应力与初始有效应力的比值对其变化趋势进行拟合,发现变化规律最为符合乘幂式关系,将数据处理后可得到其应力敏感表达式:
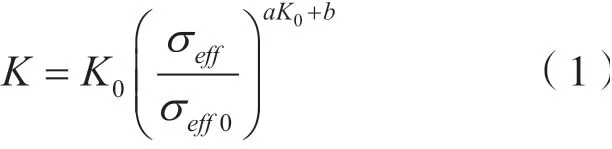
式中σeff0:岩石所受初始有效应力,MPa;K0:地层原始渗透率,mD。
应力敏感实验中将σeff0设为2 MPa,式(1)中的a、b为实验求得的常数,其中a=0.0003,b=-0.1437。由式(1)可以得出渤海高地饱压差油藏应力敏感图版(图1)。
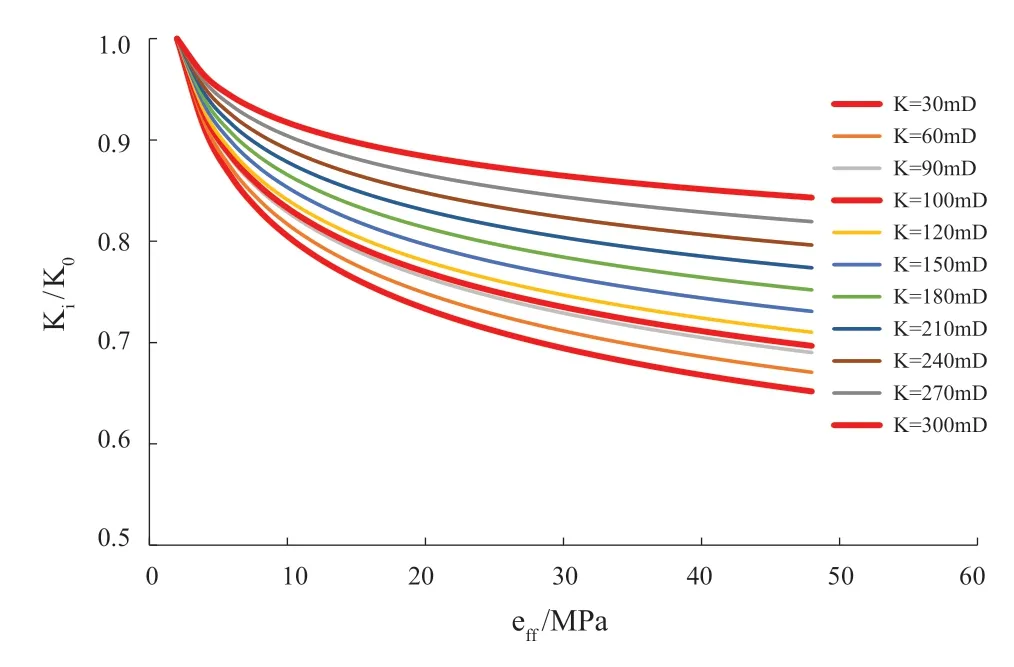
图1 渤海高地饱压差油藏应力敏感图版Fig. 1 Stress sensitivity map showing different formationsaturation pressures in Bohai highland reservoirs
2 中高渗储层考虑应力敏感的产能公式
2.1 单相油稳态产能公式
该井在流动区域内径向渗流的速度公式:

考虑应力敏感,将公式(1)代入到公式(2)中,用质量速度代替渗流速度,可得:
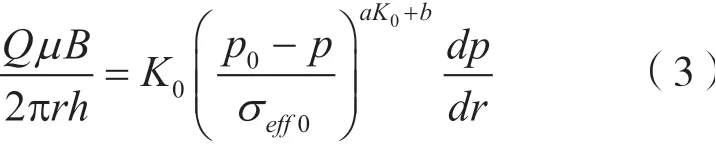
式中Q:地面的产油量,m3/s;h:油层厚度,m;p0:原始地层压力,MPa;B:原油体积系数。
对式(3)进行整理并分离变量积分得:
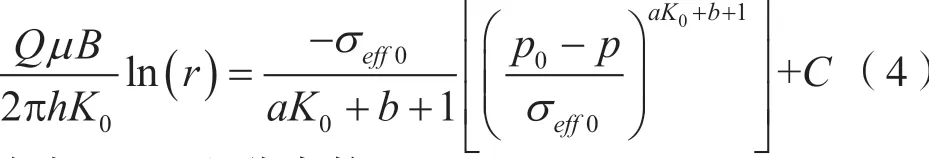
式中:C—积分常数。
根据假设条件,外边界定压为:

将式(5)代入式(4),可以求得积分常数C:
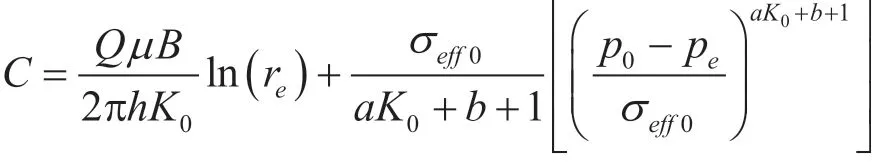
将常数C代入公式(4),可得到油藏的压力分布公式:
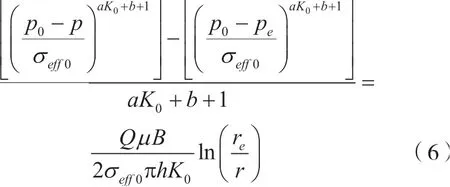
若已知井底流压pw,将其代入式(6)中,得:
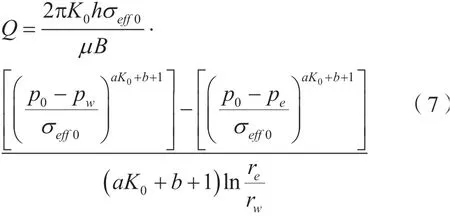
式中:rw:为井眼半径,m;re:油藏半径,m。
油指数是指单位压差下的日产油量,用公式表示为:

式中J为采油指数,m3/(d·MPa)-1;Δp为生产压差,MPa。
结合式(7)和式(8),便可得到采油指数与生产压差之间的关系:
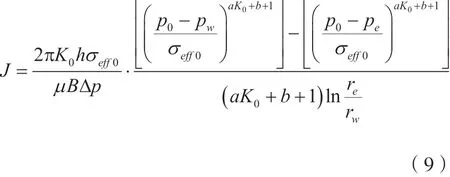
2.2 考虑脱气的稳态产能公式
当pw<pb时,考虑井筒附近脱气时,井底将出现油气两相流,可以得到pw<pb时的产能公式:
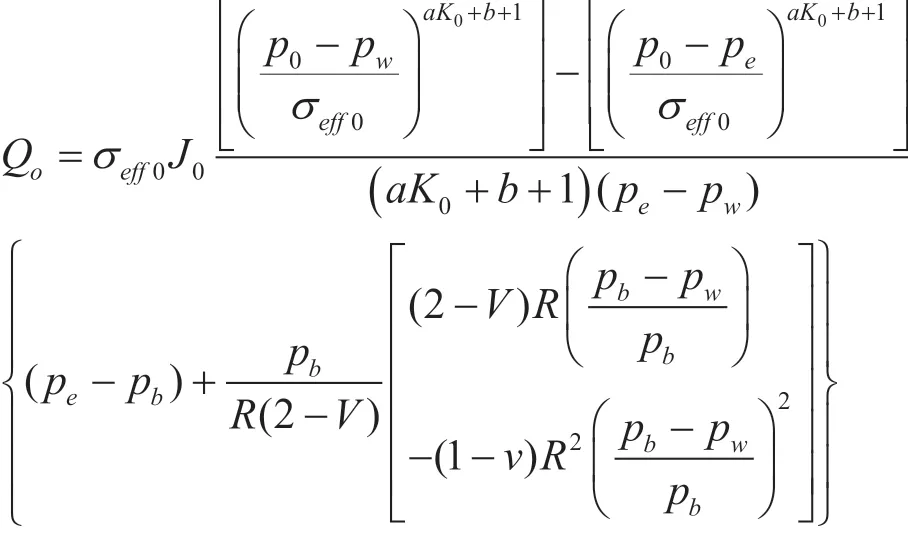
在初始开采,理想状况下,R=1,V=0.2,上式可写成:便得到了油藏考虑脱气的稳态产能公式。
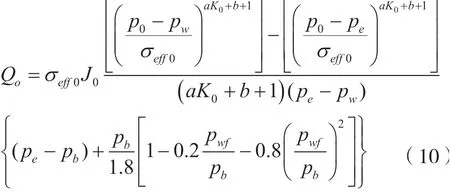
2.3 单相油拟稳态产能公式
拟稳态条件下,油井产量等于:

由于处于拟稳态阶段,地层各点压降速度dp/dt应相等,通过任一半径r断面的流量等于:
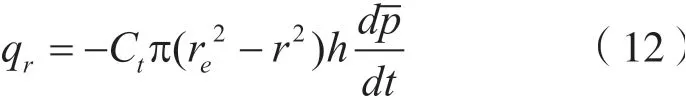
由式(11)和(12)得到:


任一断面r处的渗流速度等于:

若渗流服从达西定律,则:
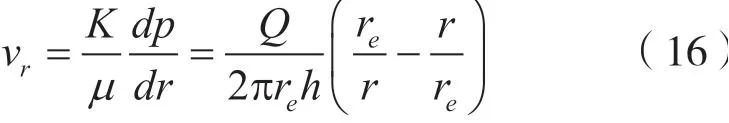
考虑渗透率的应力敏感,将式(1)代入 可得:
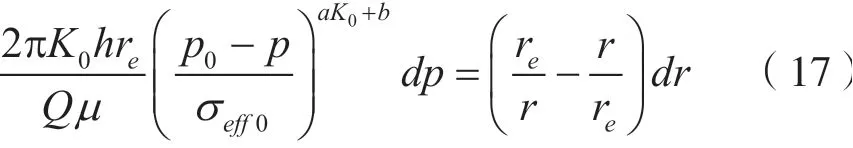
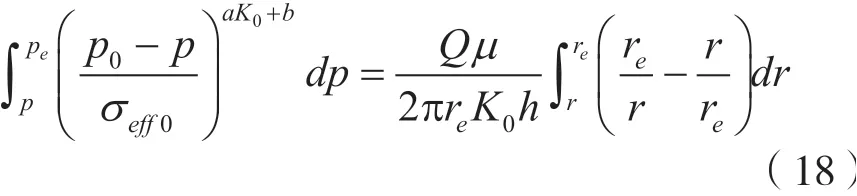
计算得:
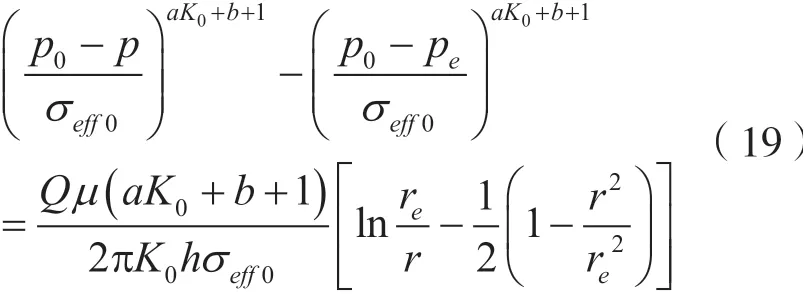
当r=rw时,p(r,t)=p w(t),由于略去得到任意时刻t时井底压力为:
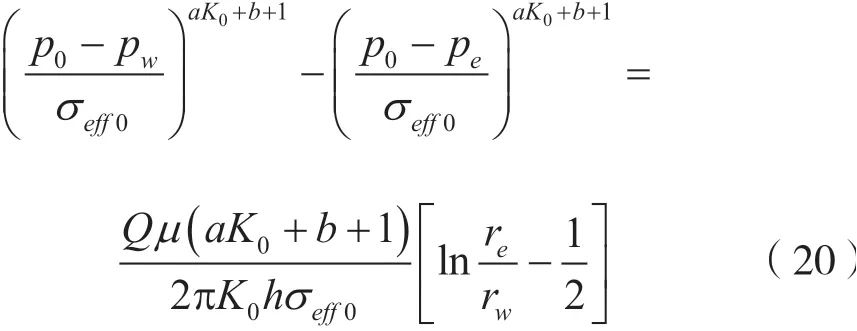
产量公式为:
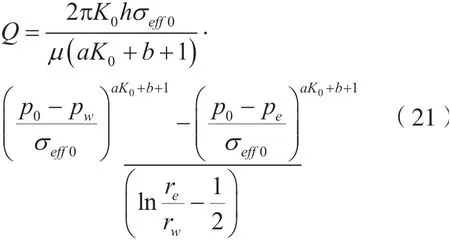
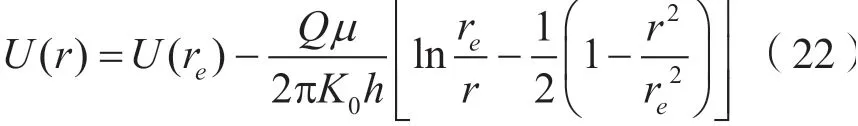
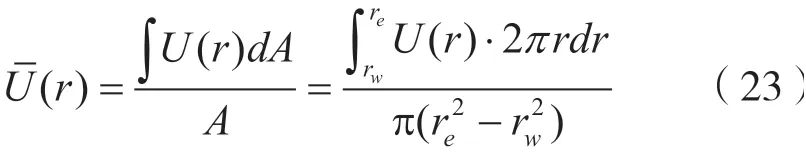
将式(22)代入式(23)中可得:

将(24)式代入(22)式可得:
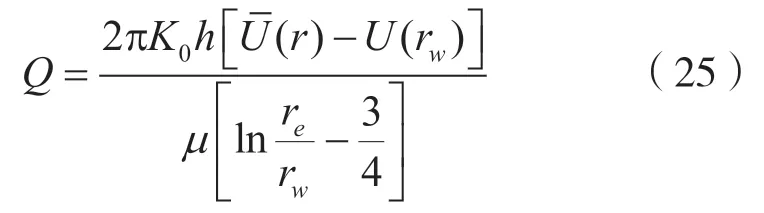
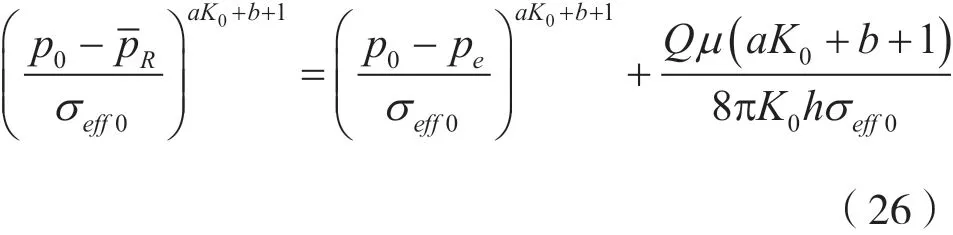
把产量方程(25)表示成压力的函数:
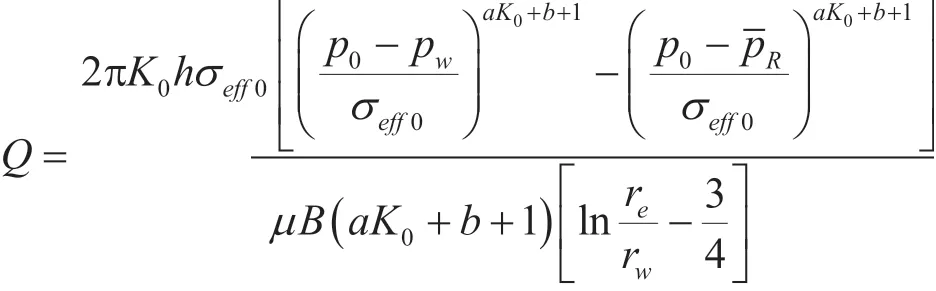
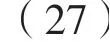
将式(26)代入式(27),可得:
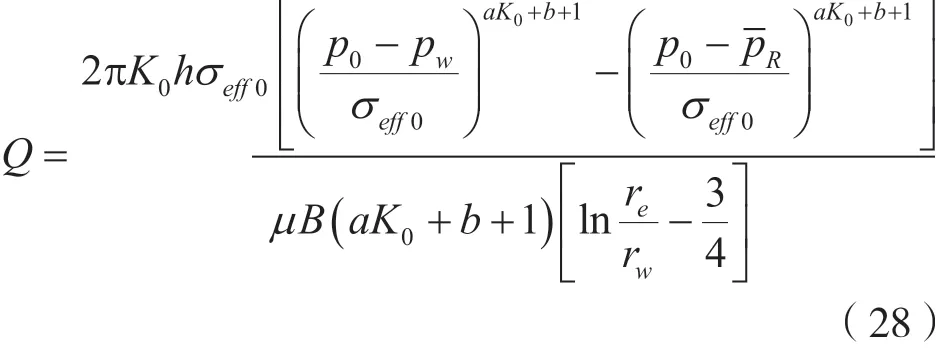
如果考虑表皮系数,并考虑表皮系数变化可得:
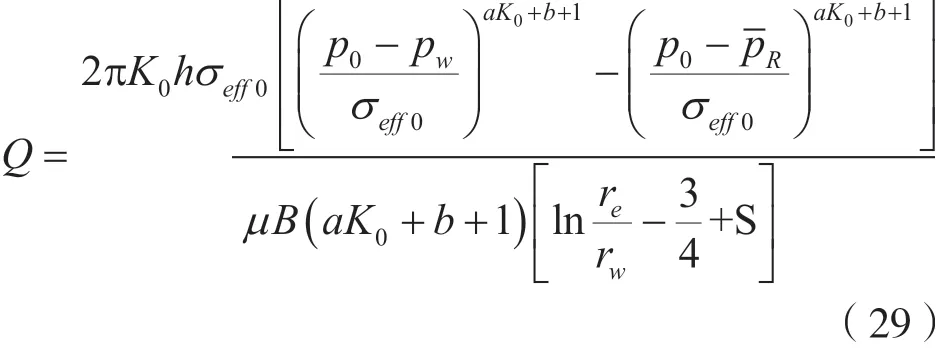
2.4 考虑脱气的拟稳态产能公式
可得采油指数J为:
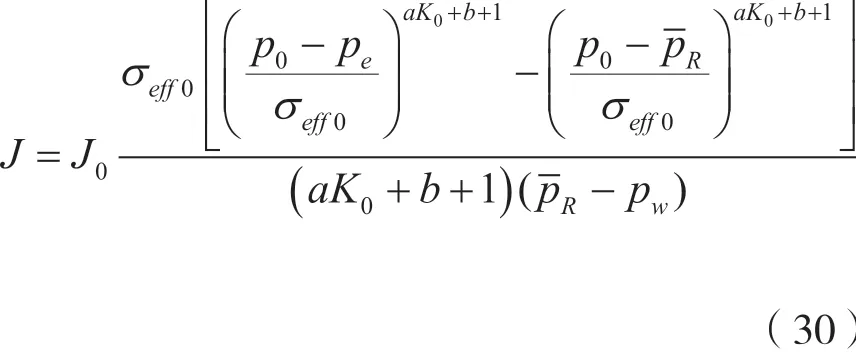
当pw<pb时,考虑井筒附近脱气时,井底将出现油气两相流,可以得到pw<pb时的产能公式:

在初始开采,理想状况下,R=1,V=0.2,上式可写成:
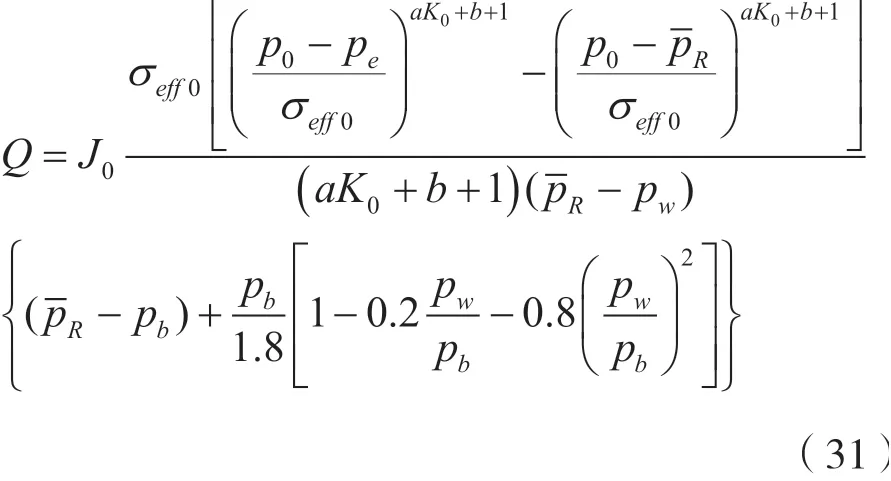
3 应力敏感影响下的产能图版
结合前文所推导的油藏产能公式,可以作出储层在稳态及拟稳态状态下的产能图版,Q油藏的参数见表2。将油藏参数代入式(10)与式(31),分别求取在稳态与拟稳态条件下,考虑脱气的储层产能曲线,绘制初始渗透率位于30~300 mD的储层的一系列产能曲线,渗透率间隔为30 mD,并绘制产能图版(图2;3)。
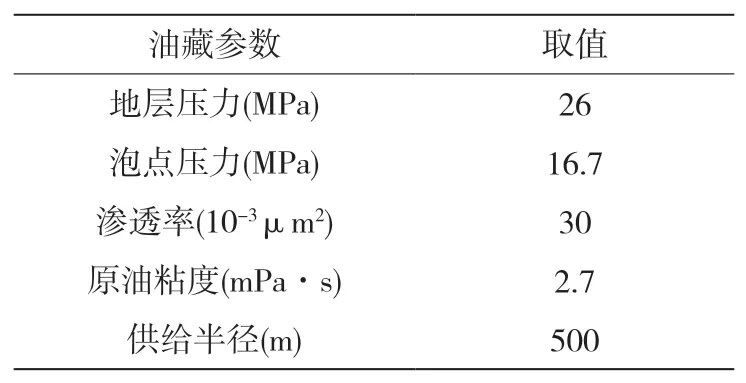
表2 Q油藏基本参数表Table 2 Basic parameters of Q reservoir
由图2与图3可以看出,随着生产压差增大,产量曲线逐渐向压力轴弯曲,储层的渗透率越小,其弯曲越强烈,应力敏感对于产能的影响随之增大。因此必然存在一个合理的生产压差限,以降低储层在生产过程中所受应力敏感影响,且此生产压差限必然随不同的储层初始渗透率改变而产生相应变化。
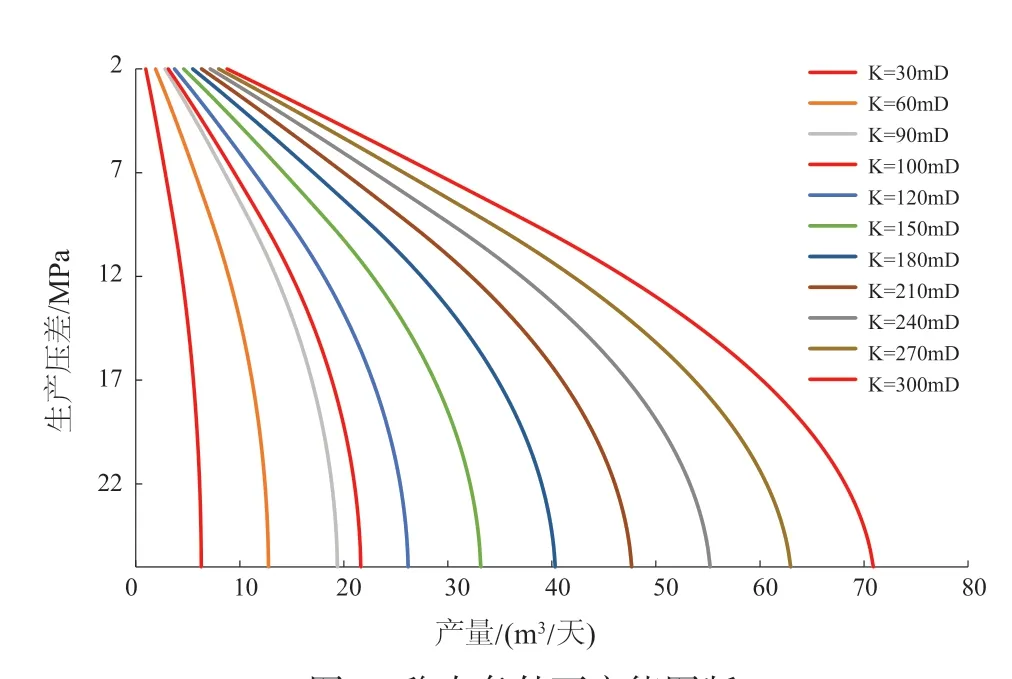
图2 稳态条件下产能图版Fig. 2 Production capacity chart under steady-state conditions
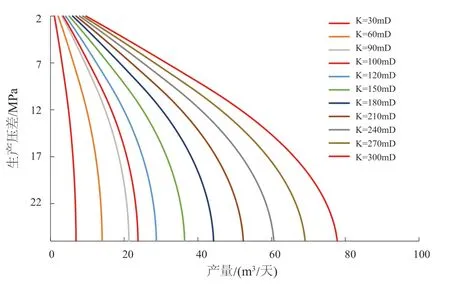
图3 拟稳态条件下考虑脱气的产能图版Fig. 3 Production capacity chart considering degassing under pseudo steady-state conditions
4 中高渗储层应力敏感影响下的合理生产压差分析
为确定储层的合理生产压差,需从产能损失的角度上,结合不同储层初始渗流透率所导致的不同比例的产能损失,得出不同初始渗透率储层所应控制的生产压差范围。
4.1 不同条件下产能对比分析
分别在稳态与拟稳态条件下,对比4种模式下的产能曲线:(1)考虑应力敏感与脱气;(2)考虑应力敏感不考虑脱气;(3)不考虑应力敏感考虑脱气;(4)不考虑应力敏感不考虑脱气(廉培庆,2011)。绘制储层初始渗透率为30 mD,稳态与拟稳态条件下的四种产能曲线(图4;5)。由图可见无论是否考虑井底脱气,油井的日产量都会受到很大程度的应力敏感影响,当井底流压过低,生产压差达到24 MPa时,产能损失可达到将近20%。
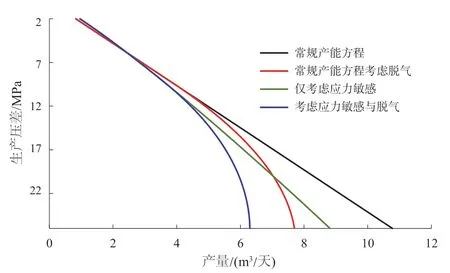
图4 稳态条件下30 mD储层不同模式产能曲线Fig. 4 Productivity curves of different modes of 30 mD reservoir under steady-state conditions
绘制储层初始渗透率为150 mD的产能对比曲线(图6;7),可以发现,产能曲线虽然受到应力敏感影响仍然有逐渐向压力轴弯曲的趋势,但与30 mD曲线相比,趋势明显变缓,当井底流压过低,生产压差达到24 MPa时,其产能损失最高达到将近14%,与30 mD曲线相比相差了6个百分点,随储层初始渗透率的增大,应力敏感对产能的影响变小,可以设置相对较低的井底流压,增大生产压差。

图6 稳态条件下150 mD储层不同模式产能曲线Fig. 6 Productivity curves of different models of 150 mD reservoir under steady-state conditions
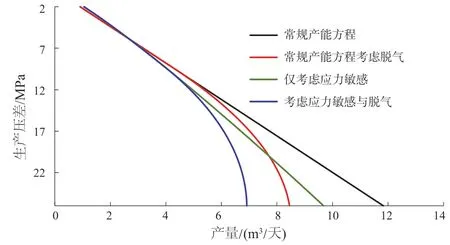
图5 拟稳态条件下30 mD储层不同模式产能曲线Fig. 5 Productivity curves of different models of 30 mD reservoirs under pseudo steady-state conditions
4.2 合理生产压差限
作出考虑应力敏感与脱气条件下,不同储层初始渗透率井底流压与产能损失比例的关系曲线(图8),可见在同一井底流压下,储层初始渗透率越低,其产能损失比例越高,即应力敏感性越强。所以应在实际生产中,应针对储层实际情况设置合理生产压差。本文仅以10%产能损失比例为生产界限,可以得到在产能损失比例不高于10%的情况下,储层的最低井底流压(表3)。

表3 储层合理井底流压Table 3 Reasonable bottom-hole flowing pressure of reservoir
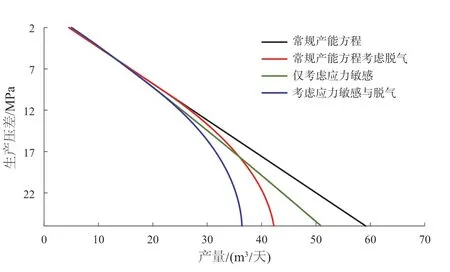
图7 拟稳态条件下150 mD储层不同模式产能曲线Fig. 7 Productivity curves of different models of 150 mD reservoir under pseudo steady state conditions
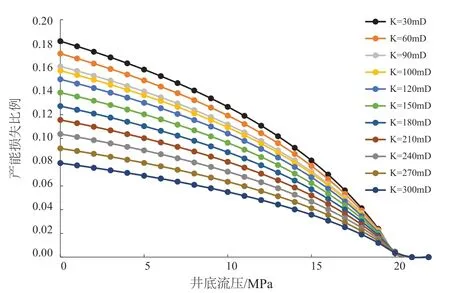
图8 井底流压与产能损失比例关系Fig. 8 Relationship between bottom hole flow pressure and productivity loss ratio
5 结论
本文针对渤海高地饱压差油藏的应力敏感特征,对其进行了相应产能分析,结论如下:
(1)渤海高地饱压差油藏的应力敏感特征更符合乘幂式关系,本文结合其应力敏感特征公式,推导得出了稳态与拟稳态条件下的单相与多相流产能公式;
(2)无论是稳态还是拟稳态条件,在储层初始渗透率保持一定的情况下,生产压差越大,即井底流压越小,应力敏感造成的产能损失比例越大,初始渗透率为30 mD的储层在生产压差高达25 MPa时,其产能损失高达20%,初始渗透率为150 mD的储层可达14%,应力敏感造成的产能损失大,应在实际生产中给予考虑;
(3)针对渤海高地饱压差油藏的应力敏感特性,结合其造成产能的产能损失,对油藏的进一步开发提出合理的生产制度优化,即随着储层初始渗透率降低,最低井底流压限也随之升高。

