基于多核学习极限学习机的助行机器人运动相容性识别①

刘 磊 杨 鹏 刘作军 宋寅卯

(郑州轻工业大学建筑环境工程学院 郑州450002)

0 引言

下肢外骨骼助力机器人是一种可为人体下肢行走提供关节助力的装置,其特点在于可以识别各种路况与步速[1-3]。由于外骨骼机器人实际运动意图与期望运动意图存在一定差异(运动不相容),穿戴者容易摔倒。外骨骼机器人的关节机构与控制方法是目前研究的热点问题,但对外骨骼机器人的运动相容性识别研究不多。当外骨骼机器人的运动轨迹与人体期望运动轨迹不一致时,为实现外骨骼助行机器人可自适应调整,本文对步幅过大、步幅过小及步幅相容3 种人机运动相容性进行识别。

表面肌电信号(surface electromyography,sEMG)是人体的一种生理信号,能够准确地反映各个肌肉的实时状态[4]。因此本文选择sEMG 作为信号源,特征提取和模式识别是其中最重要的两个环节。在众多的sEMG 特征参数提取方法中,时域特征、频域特征、时频域特征和非线性特征被证明具有良好的识别能力。

分类器的设计是模式识别领域中非常重要的环节,隐马尔可夫模型、BP(back propagation)神经网络、支持向量机(support vector machine,SVM)、极限学习机(extreme learning machine,ELM)[5]是目前常用的分类器,基于ELM 的分类模型,因其实施简单、训练时间短,已在助行机器人运动相容性识别领域取得了较好的识别结果,但是单核特征表达的单一性,限制了模型分类精度的进一步提高。为了解决此问题,本文首先从时域、频域、时频域角度提取了表面肌电信号特征,然后利用灰狼算法优化极限学习机核函数参数,最后用多核极限学习机理论,获得最优的分类模型。实验结果表明,基于多核学习ELM 的助行机器人运动相容性识别准确率较单核极限学习机有明显提高。

1 极限学习机

极限学习机可以看作是单隐含层网络,内部为全连接。其中输入层、隐含层和输出层的神经元数目分别为n和m,其结构如图1 所示。

图1 极限学习机网络结构

设输入层与隐含层、隐含层与输出层之间的连接权值分别如下:

隐含层阈值为

激活函数用g(x) 表示,输入样本数目为N,则输出Y∈Rm×N可以表示为

其中H为隐含层输出矩阵。

当g(x) 无限可微时,ELM 的参数可在训练前任意指定,且在训练过程中保持不变。输出层权值v由求解下式获得。

式(6)的解为

其中H+为隐含层输出矩阵E的广义逆矩阵。

ELM 将神经网络训练过程简化为矩阵求逆问题,学习速度明显提高。

2 多核学习极限学习机

假定n个样本,采用m个核映射函数gi映射得到m个特征值,βi表示对应核函数gi的ELM 输出权重,多核ELM[6-8]优化公式为

其中,β=β1,β2,…,βp」 表示多个核函数融合矩阵的输出权重,ξp表示第i个样本的训练误差,C表示平衡因子,γp表示第p个核函数对应的特征值的融合系数,yi表示第i个样本标签。

式(8)的拉格朗日乘子方程为

其中α和τ表示拉格朗日乘子,最优结构参数α和核融合系数τ是多核学习ELM 的重要参数,通过式(9)可求解多核ELM 最优结构参数α和核融合系数τ。

其中,K(..γ) 为多个核函数通过融合系数τ融合后的核矩阵,最后计算输出权重βp。

3 基于多核学习ELM 的助行机器人运动相容性识别

3.1 表面肌电信号采集

根据文献[9,10]的研究结果,阔筋膜张肌、股内侧肌、长收肌和股直肌针对下肢运动识别效果较好,能够得到清晰的信号,因此选择这4 块肌肉采集sEMG 信号。步幅过大、过小和相容3 种运动模式的步幅分别为700 mm、350 mm、500 mm。实验对象共6 名,实验对象均自愿参加实验并签署了知情同意书,无下肢神经及肌肉骨骼病史,在实验前被告知实验的过程及要求。每位实验对象3 种情况各采集100 组数据。表面肌电信号采用高精度、高性能的Trigno TMWireless sEMG 无线肌电采集系统,图2 为sEMG 传感器位置图,图3 为sEMG 信号采集与显示。

图2 传感器位置图

图3 信号采集与显示

3.2 信号预处理与特征提取

本文选择巴特沃斯滤波器对信号预处理。肌电信号特征值的提取是运动相容性识别的关键环节,本文采用时域特征提取法、频域特征提取法、肌电信号非线性特征提取法及小波包特征提取法[11],每名受试者的3 种运动状态都截取512 个数据点分析。小波包特征提取方法如下:参考移动窗采样方法,移动窗大小为64 点,每采集256 点后进行一次小波包分解,将4 块肌肉表面肌电信号作4 层db2 小波包分解,提取24个频带的信号并计算各频带信号能量作为特征值。排列组合熵主要是用来度量sEMG 的复杂度和非线性,通过使用排列组合熵可以评估和分析信号时间序列所呈现的一定规律性。本文选择排列组合熵表示sEMG 非线性特征,计算过程参考文献[12]的方法。表1 给出了特征值的基本意义,表2 给出了特征值的具体内容。

表1 特征属性的基本意义

表2 肌电信号特征

3.3 核函数的选择

ELM 分类器需要选择核函数,线性核函数、多项式核函数、高斯核函数和Sigmoid 核函数是目前广泛使用的核函数。

线性核函数:

多项式核函数:

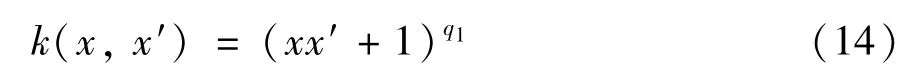
高斯核函数:

Sigmod 核函数:

本文将对表2 中时域特征、频域特征、时频域等特征选用不同的核函数得到识别结果,通过分析对比来选择最优核函数。

3.4 核参数选择

多核学习ELM 参数确定的过程相对简单,核函数参数是影响识别结果的重要参数,本文采用灰狼优化算法对核参数进行寻优。

灰狼算法是基于对自然界灰狼群的社会等级制度和围猎行为的模拟[13-14]。在D维搜索空间中,定义种群X={X1,X2,…,Xn},其中n表示种群中灰狼的个体数。定义Xi=表示第i只灰狼的位置,其中表示第i只灰狼在第d维上的位置。将在遍历种群的当前最优解记为α,将适应度当前排名次优的解记为β,将适应度当前排名第3 的解记为δ,种群中的其他个体记为ω,猎物的位置即为优化问题的全局最优解。

在围猎过程中,狼群根据下式对猎物进行包围:

式中,Xp(t) 表示种群迭代至第t代时猎物的位置;X(t) 表示第t代灰狼个体的位置;常数C表示摆动因子。

在我国现阶段的市场经济条件下，社会对于人才的需求具有自发性以及多样性的特点，在允许毕业生自主就业的基础下，政府减少了对于高校的行政约束，允许高校根据社会市场的需求进行自主设置专业和自主招生，这样有利于充分发挥市场人才资源配置的灵活性和高效性，有利于实现人才供需的有效性结合。政府需要加强对于人才资源配置的宏观调控，有利于保障人才资源和社会经济的协调发展，完善人才统计指标体系等，促进高校对于教育体系的深化改革，转变传统的教育模式，加强高校就业工作，维护社会稳定持续发展。

其中,r1=rand(0,1)。

根据下式更新灰狼个体的位置:

其中,A表示收敛因子。

其中,α随着迭代次数的增加,从2 递减至0,r2=rand(0,1)。

在狼群中,α、β、δ最靠近猎物,灰狼优化算法利用3 个个体来确定是否为最优解。在灰狼群中,个体围杀猎物行为的数学描述如下。

计算在第t代时,α、β、δ对种群内灰狼个体位置的影响X1、X2、X3,如下:

式中,Xα(t)、Xβ(t)、Xδ(t) 表示种群迭代至第t代时α、β、δ的位置,X(t) 表示第t代灰狼个体的位置,C1、C2、C3和A1、A2、A3表示不同的摆动因子与收敛因子。

3.5 基于多核学习ELM 运动相容性识别流程

利用多核学习ELM 进行运动相容性识别具体步骤如下。

(1)采集6 名实验对象3 种运动模式下的sEMG。

(2)利用巴特沃斯带通滤波器对sEMG 滤波处理,并将处理后数据的50%选为训练样本、50%选为测试样本。

(3)采用3.2 节方法对预处理后的sEMG 从不同角度进行特征提取。

(4)构建多核学习ELM 分类模型,利用灰狼算法寻找分类器中最优核函数参数。

(5)利用训练样本训练多核学习ELM 分类器的性能,利用测试样本检验训练效果,得出识别结果。

识别流程如图4 所示。

图4 算法流程图

3.6 实验结果分析

本文按照3.1 节方法采集sEMG,利用巴特沃斯带通滤波消除因零点漂移所产生的基线。图5 为步幅过大、过小、相容时长收肌信号图。图6 为步幅过大不相容运动模式中股内侧肌原始sEMG、巴特沃斯滤波sEMG、整流sEMG 波形对比。

图5 步幅过大、过小、相容长收肌信号图

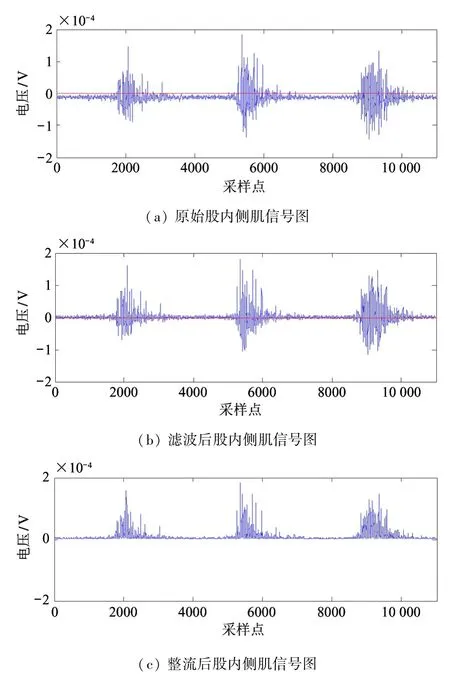
图6 整流前后股内侧肌波形对比

对每组数据分别提取4 种sEMG 特征参数,分别是时域特征、频域特征、灰度矩特征和小波域特征,按照式(28)对特征参数进行归一化处理。

其中,x、xnew分别表示归一化前后的数据,xmax和xmin分别表示数据的最大值和最小值。

由表3 可见,时域特征的最佳核函数是高斯核函数;时频域特征的最佳核函数是高斯核函数;频域特征的最佳核函数为Sigmod 核函数;非线性特征的最佳核函数为多项式核函数。利用最优核函数组合多核核函数,表4 给出了最优核组合。

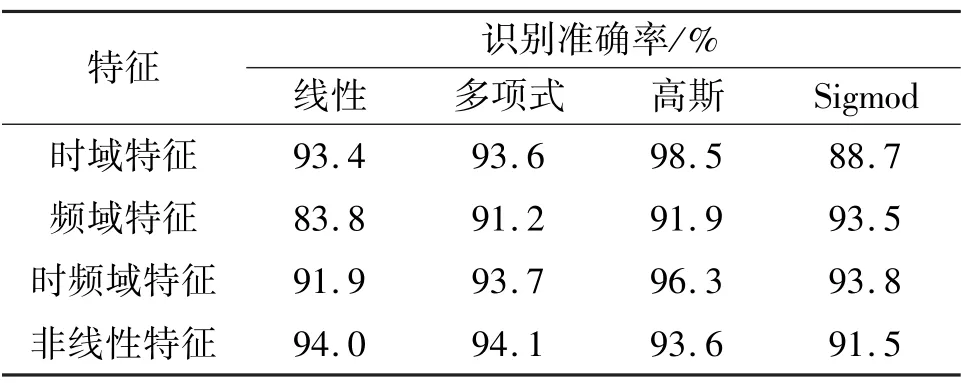
表3 单核ELM 识别结果

表4 最优核函数组合

根据表4 的最优组合构造多核ELM 分类模型,并对参数利用灰狼算法寻找最优核函数参数。灰狼算法参数设置如下,初始种群规模为30,最大迭代次数为300,维度为20,运行次数为20,灰狼算法中的反向学习优化选择概率p=0.5。采用5 折交叉验证的识别准确率作为适应度函数。经过20 次计算求均值,表5 给出了最优核函数参数。将参数优化之后的多核学习ELM 分类器应用于测试样本,结果如图7 所示。可以看出,4 种单核ELM 用于不同特征参数的运动相容性模式识别时,识别准确率差异很大,即单一核函数应用于不同特征空间时,无法保证稳定的高识别率;而多核学习ELM 不但保证了在每个特征空间提供最优识别率,而且在时频域特征空间中把识别正确率从92.6%提高94.7%。

表5 最优核函数参数

图7 不同ELM 核函数与多核学习ELM 对比实验结果

本文运用SVM、多核学习SVM、ELM、多核学习ELM 4 种识别方法进行运动相容性识别。为了更好地比较4 种方法的识别结果,选择了Matlab 中的方差分析(analysis of variance,ANOVA)的统计学方法进行分析,显著性系数选择均为P=0.05。

首先对6 位实验对象基于多核学习SVM、SVM、ELM、多核学习ELM 4 种识别方法的识别结果进行比较。图8 给出基于SVM、多核学习SVM、ELM、多核学习ELM 平均识别准确率分别为87.00% ±3.66%、89.66% ±3.58%、91.37% ±4.31%、94.37%±4.31%。经ANOVA 分析发现,无论是SVM 还是多核SVM 均与多核学习ELM 方法存在显著性差异(P＜0.01),可以看出多核学习ELM 模式识别方法比SVM、多核学习SVM 模式识别方法更适合相容性识别。对于ELM 与多核学习ELM 的识别结果进行ANOVA 分析发现并无显著性差别(P=0.9517),从实验结果来看,多核学习ELM 要略优于ELM 方法。

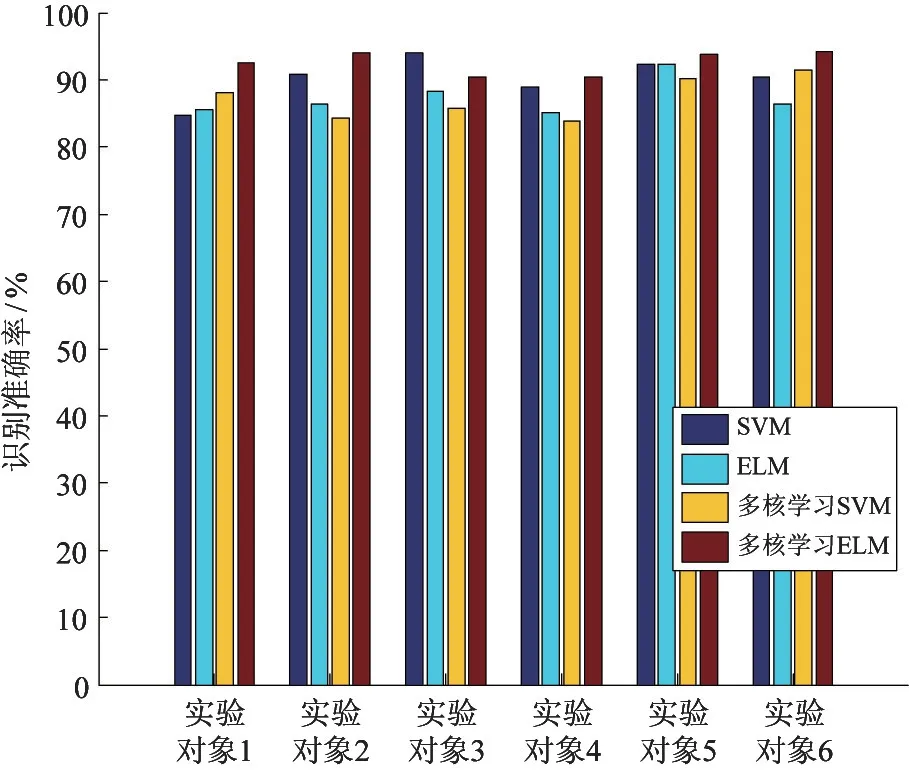
图8 4 种方法对比实验结果

为了更清晰地分析不同方法的准确率差异性,将6 位实验对象的每一类运动的识别准确率进行统计平均,得到结果如表6 所示。从表6 中可以看出,仅对步幅过大的情况基于ELM 识别方法的准确率略高于多核学习ELM 方法,对于步幅过小、步幅相容情况多核学习ELM 方法均有明显的优势,对于助行机器人运动相容性识别来说,多核学习ELM 方法性能更好。

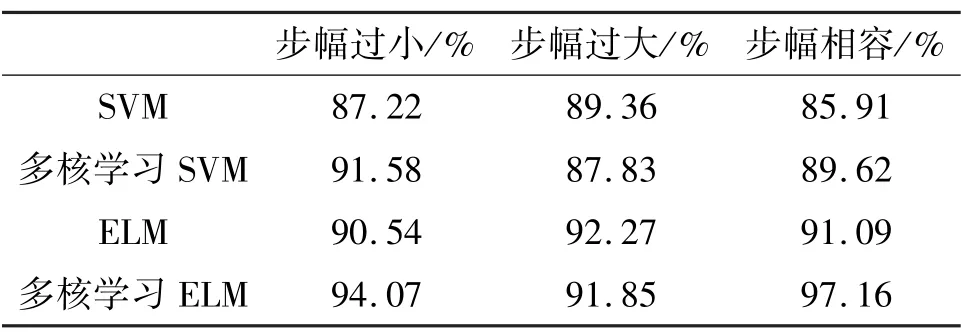
表6 不同方法每一类运动的识别准确率

4 结论

本文研究了一种基于多核学习ELM 的助行机器人运动相容性识别方法,把采集到的4 个特征空间的特征数据作为分析对象进行助行机器人运动相容性识别研究,得出以下结论。

(1)多核学习ELM 融合了多种sEMG 特征,能够较为全面地描述运动信息。

(2)多核学习ELM 分类器针对每个运动特征空间分别选取最优核函数,并利用灰狼算法实现了核参数的优化配置。

(3)实验结果表明,多核学习ELM 分类器可以通过不同核函数融合任意多组运动特征信息,识别准确率优于ELM 和单核SVM,具有较好的实用性和推广性。