地铁列车制动仿真软件的开发

韩 龙，王 岩，贺竹林，周俊超

（中车青岛四方机车车辆股份有限公司，青岛 266111）

我国轨道交通行业蓬勃发展，在线运营的轨道车辆也迎来了爆发式的增长。随着各地地铁建设的浪潮，地铁车辆的安全性更加重要。为了更好地了解制动系统运行状态，可通过对制动系统进行仿真，模拟车辆在线路运行状态下的制动过程。仿真模拟方便快捷，参数调整简单，可参与地铁列车制动系统的设计和优化，可节约昂贵的测试费用。因此，制动系统建模问题已引起研究人员的关注。

Piechowiak[1-2]开发了一个具备复杂的分布式设备和制动管路配置的制动系统仿真模型，是一列货运火车的仿真模型。Pugi等人[3]将货运列车制动系统分解成许多子组件，并通过Matlab-Simulink程序内置制动系统模型组件库。通过上述分析笔者开发的模型可以得到比较准确的模拟结果，运行这些仿真模型需要非常大的计算量。本文采用了简化的模型，需要的计算时间大幅减少，便于实时仿真。

本文建立的软件模拟地铁列车的制动过程，该软件由用户图形界面和仿真模型构成。用户图形界面用于提供一个用户和仿真模型之间的交互通信窗口。仿真模型包括车辆子模型和制动系统子模型，模拟过程中用户可以通过用户图形界面修改参数。

1 软件结构

软件的结构简图，如图1所示。软件包括仿真模型和图形用户界面。仿真模型由地铁列车子系统模型和制动系统子模型构成，其彼此间通过软件内部数据进行通信，内容包括列车实时的制动力、轴的旋转速度和车辆重量等数据。

图1 软件结构

用户图形界面的计算机代码由LabVIEW程序开发的。底层模型是使用Matlab-Simulink程序建立。采用仿真接口工具包（SIT，Simulation Interface Toolkit）来建立用户图形界面和底层模型之间的通信。

2 仿真模型

软件仿真模型提供虚拟的地铁列车和虚拟的制动系统，在用户图形界面的参数控制下，对地铁列车的制动效果进行仿真计算，并将仿真结果输出给图形用户界面。

2.1 车辆子模型

车辆子模型模拟与制动过程是相关的单节车辆和多节车辆之间的变量，包括：车辆位移、速度、减速度，轮轨粘着工况，轴重转移，闸瓦摩擦系数变化、坡道坡度和运行阻力等[4]。

在建模过程中，需要根据车辆对制动过程的影响大小，对模型进行简化[5]。车辆子系统模型主要考虑车辆的垂向、伸缩和点头自由度，其原因有两方面：（1）地铁列车的制动过程主要与车辆的垂向、纵向、点头自由度有关；（2）如果要完全考虑车辆各部件的所有自由度（包括垂向、伸缩、点头、横向、侧滚、摇头），建模的难度将增大，仿真很难得到收敛，对计算机资源需求也大大增加。

2.1.1 车辆子模型简化内容

简化的车辆子模型，如图2所示。模型简化内容包括：

图2 简化的车辆子模型

（1）地铁列车选取典型的6辆地铁地铁列车编组，简化为两个3辆编组；

（2）转向架的垂向悬挂通路，考虑一、二系悬挂的刚度和阻尼；

（3）转向架和车钩的纵向牵引通路，忽略纵向的牵引刚度和阻尼，认为车体与构架、构架与轮对之间在纵向上是刚性连接；

（4）车辆之间仅保留了车钩连接，车钩简化为刚度阻尼模型；

（5）认为车体和转向架的质量为对称分布、忽略轨道不平顺的影响、同一辆车的各轮对所处的坡道的坡度认为是一样的。

2.1.2 简化后需要的参数

（1）简化后需要的自由度以图2中单节车辆模型车为例，包括：车体的浮沉和点头，两个转向架构架的浮沉和点头，4条轮对的转动和每辆车的平动。

（2）车辆子模型建模时需要用到的车辆尺寸参数，如图3所示，包括：前后转向架牵引中心销距离Lc，转向架轴距Lb，车体重心高度Hc、转向架（除轮对外）重心高度Hb，转向架与车体间的牵引拉杆在构架端的牵引点高度Hbc1，转向架与车体间的牵引拉杆在车体端的牵引点高度Hbc2，车钩的牵引点高度Hcp，车轮半径Rw，闸瓦/闸片的等效作用半径Rbr和电制动力的等效作用半径Rebr。

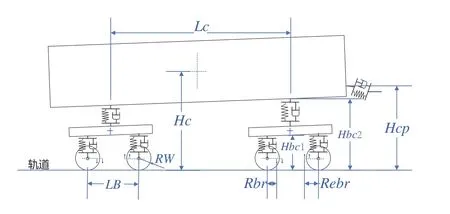
图3 车辆模型主要尺寸参数

（3）在Matlab-Simulink中，建立车辆子模型各主要部分的子模型，包括轮对子模型、弹簧阻尼子模型、构架子模型、车体子模型，这些子模型在Matlab-Simulink环境下装配车辆的初步模型；组装初步模型和耦合器元件模型，构建完整的车辆子模型[6]。

2.2 制动系统子模型

2.2.1 制动系统模型分类

（1）制动系统模型分为空气制动系统模型和电制动系统模型两部分。由于制动系统的复杂性，若像车辆子模型那样细致建模将很难在仿真过程中得到收敛解，导致仿真结果与实际制动系统的输出相差极大，且建立制动系统细致模型难度极大。因此，制动系统只建立“黑箱模型”。

（2）所谓制动系统的“黑箱模型”，是指在建模时预先设置好由试验得到的固定制动级位指令下的制动缸响应曲线。在仿真过程中，系统接收软件界面输入的制动指令信号，通过对预先设置的试验曲线进行插值计算得到仿真所需要的制动缸压力响应曲线。用“黑箱模型”的方法建模既能减小建模工作量，同时又能使仿真结果与实际制动系统试验数据相符。

2.2.2 制动模型建立原理

下面以空气制动系统为例说明制动系统“黑箱模型”的建立原理。制动系统的压力响应曲线一般无严重的超调现象，因此，可以用经典控制理论中的惯性环节建模，如图4所示。在建立空气制动系统模型时，将试验所得的固定制动级位的制动缸压力曲线预置在空气制动系统模块中，在仿真时空气制动系统模块将会根据输入的制动指令插值计算出该指令所对应的制动缸压力曲线，进而输出制动缸压力。电制动系统的“黑箱模型”同样可以用这种方法进行建模。

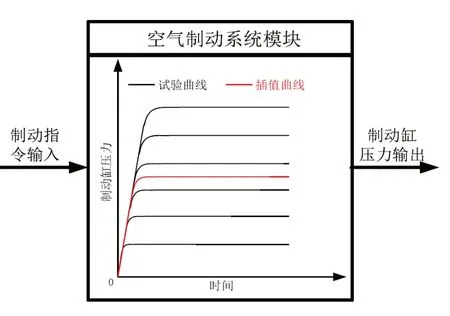
图4 空气制动系统的“黑箱模型”示意

为优化仿真计算，减少计算机的工作量，制动系统模型基于相关文献中的实验数据进行了简化。一阶滤波器的时间延迟可用于空气制动系统模型，见式（1）[7-8]：

其中，S—Laplace算子；

Pcy—制动气缸内的空气压力；

Pr—制动缸目标压力；

τ—惯性环节的时间常数（与制动力的响应时间有关）；

Td—制动阀的延时响应时间；

K—常数。

参数Kbr，τ和Td可以通过比较仿真和使用最小二乘法进行测试的结果来确定。

由闸瓦施加在一个轮轴的总摩擦力Fpad可通过式（2）计算：

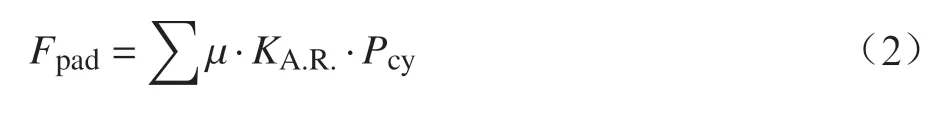
其中；μ—车轮踏面和闸瓦的摩擦系数；

KA.R.—考虑到圆柱体有效截面积和吊挂因数的常数。

2.3 仿真模型搭建

搭建完成的车辆子模型搭配制动系统子模型，再以车辆编组的形式搭建成仿真软件的仿真模型。图5所示为仿真软件的仿真模型建模流程。图6所示为仿真软件底层模型的子模块关系。

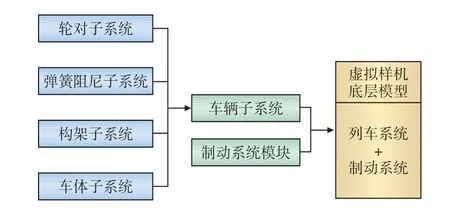
图5 仿真软件的底层模型建模流程

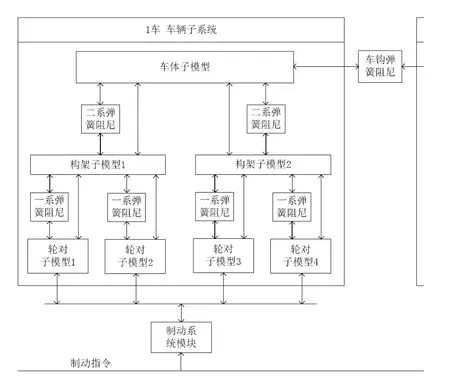
图6 仿真软件底层模型的子模块关系

3 用户图形界面

用户图形界面包括主界面和辅助界面，作用是仿真进行之前初始化车辆参数、制动相关参数、仿真结果输出显示以及数据存储。车辆参数包括地铁列车质量、车体转动惯量、转向架构架和轮对参数、车辆尺寸（车体重心高度，车轮滚动半径等）、悬挂刚度和阻尼等；制动相关参数包括制动指令、制动初始速度，轨道坡度等；仿真结果包括制动力、制动距离、每个车的速度和减速度、各轴轴重和旋转速度、车钩力等。

主界面如图7所示，其左边部分是用来设置模型参数，右边部分是用来显示模拟结果。主界面是仿真过程所用到的主要人机交互界面。

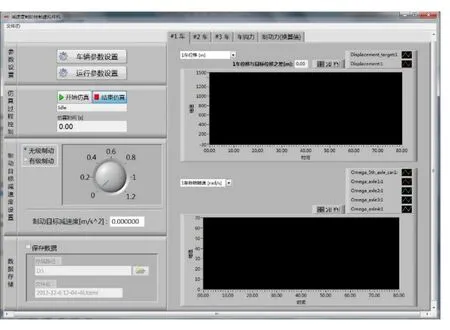
图7 主界面

辅助界面如图8所示，负责在后台与Simulink搭建的车辆子模型和制动系统子模型进行通信和数据交换。

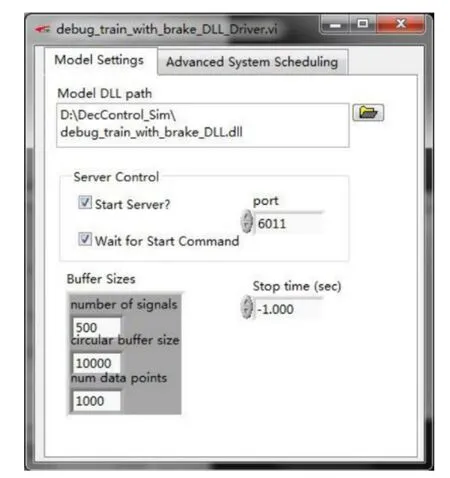
图8 辅助界面

4 仿真过程

点击“车辆参数设置”按钮，即可设置车辆参数，如图9所示。

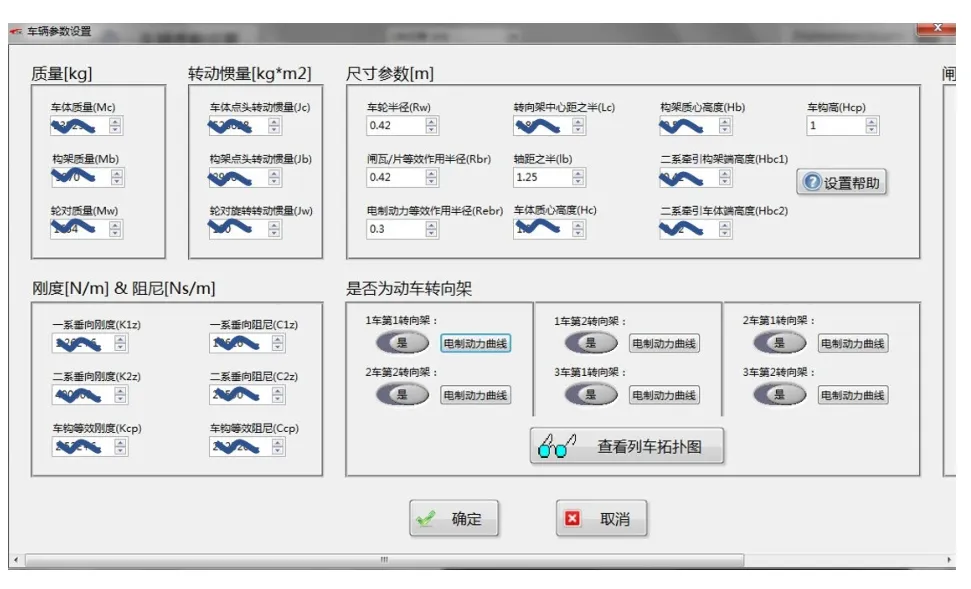
图9 车辆参数设置

点击 “运行参数设置”按钮，即可设置地铁列车运行环境参数，如图10所示。

图10 运行参数设置

正确设置试验参数后，即可执行仿真计算。图11所示为某型地铁列车仿真结果，浅色线（黄色）为预设的理想状态下的目标减速度曲线，深色线（红色）为软件仿真计算的实际减速度。从该图中可看到，在软件仿真计算得到的实际减速度与预设目标减速度能实现比较精确的跟随，仿真结果准确可信。

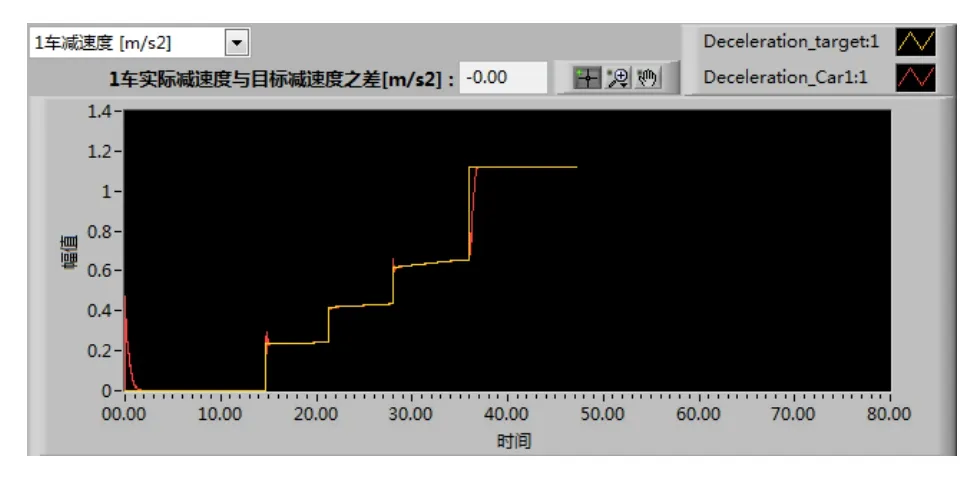
图11 制动减速度仿真计算结果示意

5 结束语

地铁列车制动仿真软件已经建立完成，它由用户图形界面和仿真模型组成。仿真模型利用Matlab-Simulink建立，包括车辆子模型和制动系统子模型。车辆子模型由与制动相关的车辆子单元模型建立。制动系统子模型经过简化并基于实验数据构建，以减少计算量。图形用户界面通过LabVIEW程序开发，用于输入模型参数、显示仿真结果并存储仿真数据。

本软件使用了简化的车辆和制动系统模型，计算时间显著缩短，仿真过程与真实制动过程可达到实时同步。