基于ST-EKF与滤波增益约束的加速度计微g级标定

郭 航，吴文启，王茂松，崔加瑞

(国防科技大学智能科学学院，长沙410073)

0 引言

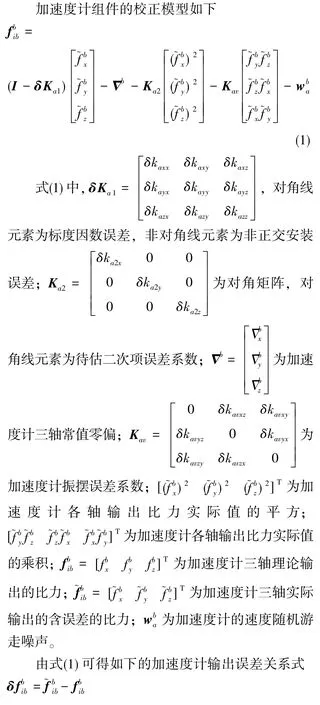
在系统级标定中考虑加速度计组件的非线性误差，精确标定包括二次项误差、振摆误差在内的各项误差，将有效提高导航精度。尤其，当捷联惯性导航系统惯性测量单元(Inertial Measurement Unit，IMU)处于大水平倾角情况下，二次项误差、振摆误差将成为影响加速度计组件输出精度的重要误差源，对二次项误差、振摆误差的精确标定与补偿将极大提高大水平倾角下惯导系统的导航精度。

惯性测量单元的系统级标定主要是建立包含待估计误差系数在内的误差模型，通过将如速度误差、位置误差等导航输出误差作为观测量对惯性器件的误差参数进行估计。文献[1]指出了系统级标定相对于分立式标定的优势，表明系统级标定不需要依赖高精度转台，适用于自标定与外场标定，因而得到国内外诸多学者的深入研究。文献[2]～文献[6]对惯性测量单元的系统级标定技术进行了相关研究，文献[2]提出了一种基于逆向导航的双轴旋转惯导系统自标定方法，但是只完成了惯性测量单元部分误差参数的系统级标定；文献[3]针对双轴旋转激光惯导系统提出了一种在线自标定方法，但是没有对IMU振摆误差进行标定；文献[4]考虑了内外杆臂误差，针对激光捷联惯导系统提出了一种高阶Kalman滤波的系统级标定方法；文献[5]提出了一种八位置的系统级标定方法，考虑了温度的影响，但只估计了惯性测量元件的线性误差；文献[6]总结了惯性测量元件的各种标定方法以及标定技术的发展方向。可以看出，文献鲜少同时考虑将加速度计组件的二次项误差、振摆误差作为状态变量进行估计，一方面是考虑到加速度计组件振摆误差的弱可观性，会导致通过传统扩展 Kalman滤波(Extended Kalman filter，EKF)算法所估计出的结果不准确；另一方面仅仅标定出加速度计的线性误差或进一步标定出加速度计的二次项误差即可满足一般惯性导航的实际精度需求。为了提高状态变量估计的准确性，国内外学者也做了许多研究工作，例如，文献[7]为解决动态环境下滤波的局部可观测性与误差协方差矩阵估计不一致问题，提出了一种状态变换扩展Kalman滤波(State Transformation Extended Kalman Filter，ST-EKF)算法；文献[8]为实现滤波增益矩阵与滤波状态估计可观测性的一致性，从而提高定位精度与姿态跟踪精度而提出了Schmidt-Kalman滤波(Schmidt Kalman Filter)；文献[9]为解决传统Kalman滤波器对协方差估计不一致造成对弱可观或不可观状态变量的错误估计问题，引入了可观测约束Kalman滤波等。

本文通过三个方面来实现对加速度计组件的微g级精确标定：1)推导并建立包含标度因数误差、安装误差、零偏、二次项误差、振摆误差在内的加速度组件误差模型；2)将1)中建立的误差模型中所有误差参数作为状态变量构建基于状态变换扩展Kalman滤波(ST-EKF)的系统方程，以导航解算速度作为量测值，激励出待估计误差参数；3)为进一步解决滤波状态协方差阵计算误差问题，提高待估计误差参数的准确性，采用以Schmidt滤波为基础对滤波增益矩阵进行约束的方法，通过调整滤波增益矩阵K的值，使得在编排的23个非倾斜位置上估计出标度因数误差、安装误差、零偏、二次项误差，在12个倾斜位置上估计出振摆误差。相比于传统的基于扩展Kalman滤波的系统级标定算法，状态变换扩展Kalman滤波(ST-EKF)通过将滤波器状态转移矩阵中的比力项变换为当地重力加速度，解决了转台在翻滚时状态转移矩阵计算的不准确对滤波精度的影响。根据系统级标定过程中状态的实际可观测性对滤波增益进行约束，避免了对弱可观或不可观状态的错误估计，使参数估计更加准确。

1 一种基于ST-EKF与增益约束的加速度组件系统级标定方法

使用Kalman滤波算法对加速度计组件进行各项参数的估计，应用于实际系统长时间使用后需要进行精确标定的场景。由于捷联惯导在出厂前已经经过了一次标定，于是再标定时的各误差将都是微小量。

取静止状态下惯导解算的速度与实际速度的差作为观测量，观测方程如下所示

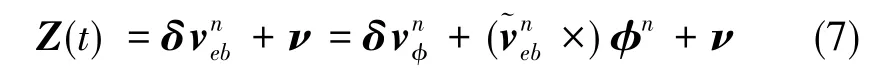
于是得到观测矩阵H

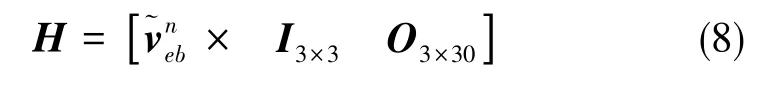
式(7)、式(8)中，Z(t)为观测向量，ν为随机白噪声，其他符号与上文中的定义保持一致。

系统级标定采用多位置静止标定，标定过程通过陀螺模值来区分静止数据段与翻滚数据段。

理论上，弱可观误差状态估计的准确性更加依赖于状态协方差阵计算的准确性。传统的基于EKF的系统级标定算法由于对状态协方差阵P的计算不够准确，从而不适用于对弱可观状态的精确估计。然而，基于ST-EKF的系统级标定算法将导航误差方程中的比力项用重力项替代[10]，可更准确计算出状态协方差阵P。 同时，将ST-EKF与滤波增益约束相结合，进一步避免了在非倾斜位置上对振摆误差的错误估计，同时在其他误差状态估计结束后，通过斜置IMU使弱可观的振摆误差最终得到准确估计。

由振摆误差的来源机理可知，当IMU处于非倾斜位置时，将激励不出振摆误差，因此如果整体估计，将会由于协方差矩阵的计算误差造成在非倾斜位置上估计出不准确的振摆误差系数。于是借鉴Schmidt滤波器的原理，调整与状态变量对应的滤波增益变化，在非倾斜位置(式(9))和倾斜位置(式(10))上设置滤波增益矩阵

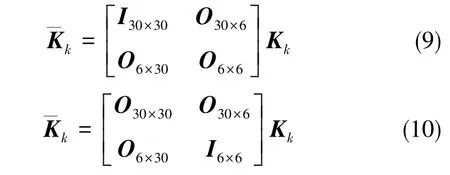
式(9)、式(10)中，Kk为tk时刻的滤波增益矩阵，为根据状态可观测性借鉴Schmidt-Kalman滤波约束后的tk时刻的滤波增益矩阵。从而在非倾斜位置上只估计出标度因数误差、安装误差、零偏、二次项误差，在倾斜位置上只估计振摆误差而不改变已经估计出来的其他各项误差参数。

判断加速度组件是否处于倾斜位置，可以通过各轴输出比力值与当地重力加速度模值的大小来判断。在实验室内标定的加速度计尺寸效应参数不会变化，再次标定时不考虑该误差系数的变化。

2 实验验证与分析

2.1 实验设备与条件

为验证本文提出的一种基于ST-EKF与滤波增益约束系统级标定算法的有效性，需借助SGT-3三轴惯导测试转台实现对惯导系统的位置编排。为减少温度对惯性器件各项误差的影响，在进行标定实验之前充分预热，保证惯导系统温度基本稳定后，再开展标定实验。

实验选择某型光纤陀螺捷联惯导系统，加速度计与陀螺的指标参数如表1、表2所示。

表1 某型惯性导航系统加速度计指标参数Table 1 Performance parameters of accelerometer in the inertial navigation system

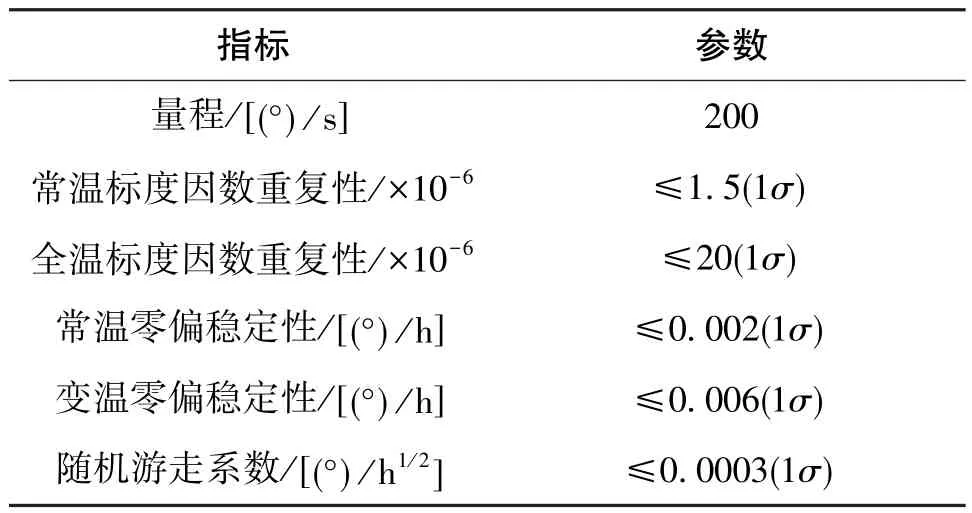
表2 某型惯性导航系统陀螺指标参数Table 2 Performance parameters of gyroscope in the inertial navigation system

2.2 实验内容与分析

将光纤惯导系统固定在三轴惯导测试转台上，通过编排23＋12位置估计出加速度计组件的各项误差参数：23个非倾斜位置估计出加速度计组件的标度因数误差、安装误差、常值零偏、二次项误差系数，12个倾斜位置估计出加速度计组件的振摆误差系数。通过6个大水平倾角位置的重力残差验证了标定结果的正确性以及估计振摆误差的必要性，最后对比不同补偿模型时水平姿态角变化情况下纯惯导解算的位置误差，再一次验证了估计结果的正确性和估计振摆误差的必要性。

标定实验所需的三轴惯导测试转台如图1所示。图1中，光纤惯导系统被固定在转台上。

图1 三轴惯导测试转台实物图Fig.1 Physical map of three axis inertial navigation test turntable

23＋12位置编排如图2、图3所示。

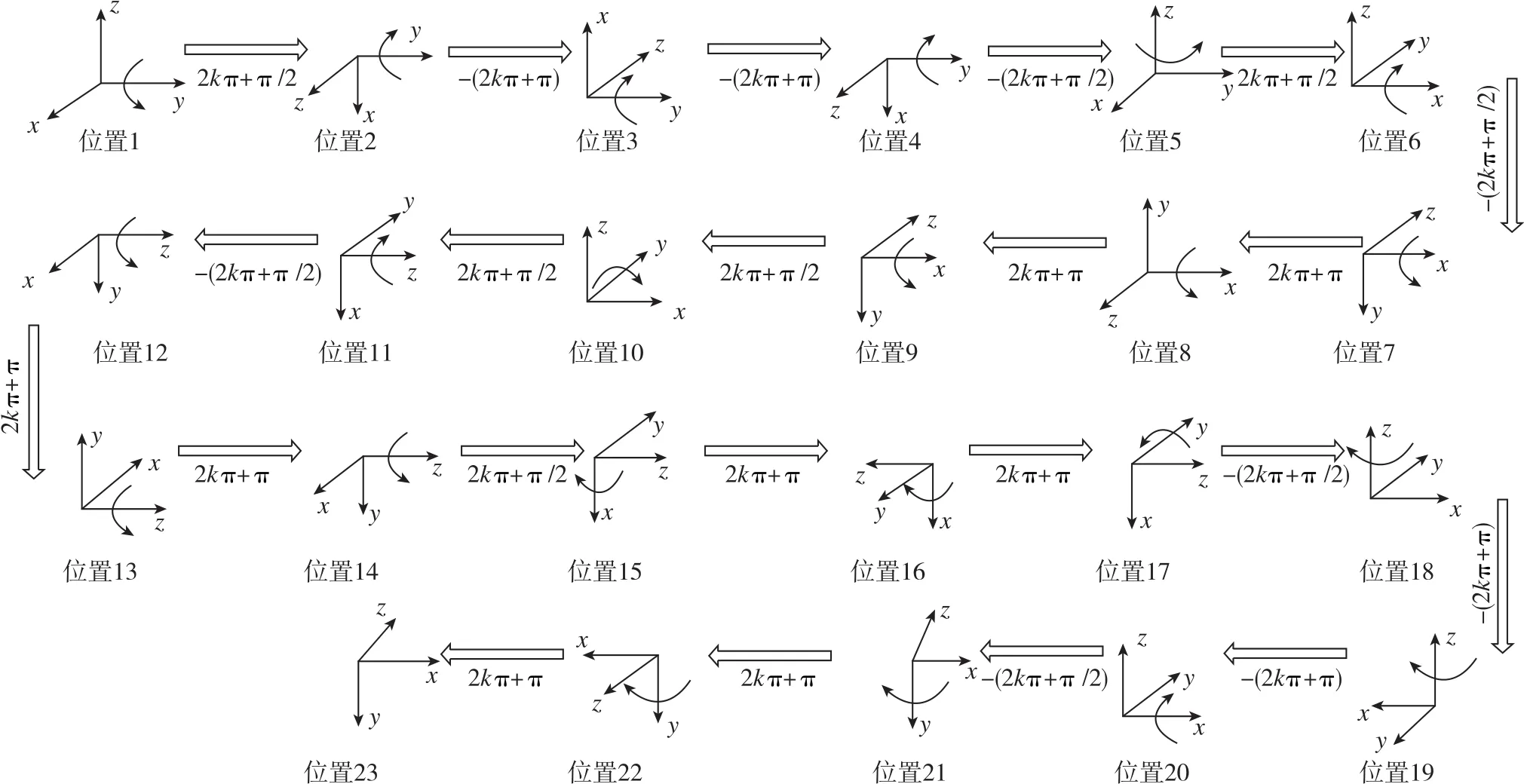
图2 系统级标定实验非倾斜23位置编排Fig.2 Twenty-three non-tilting positions and rotations in systematic calibration experiments

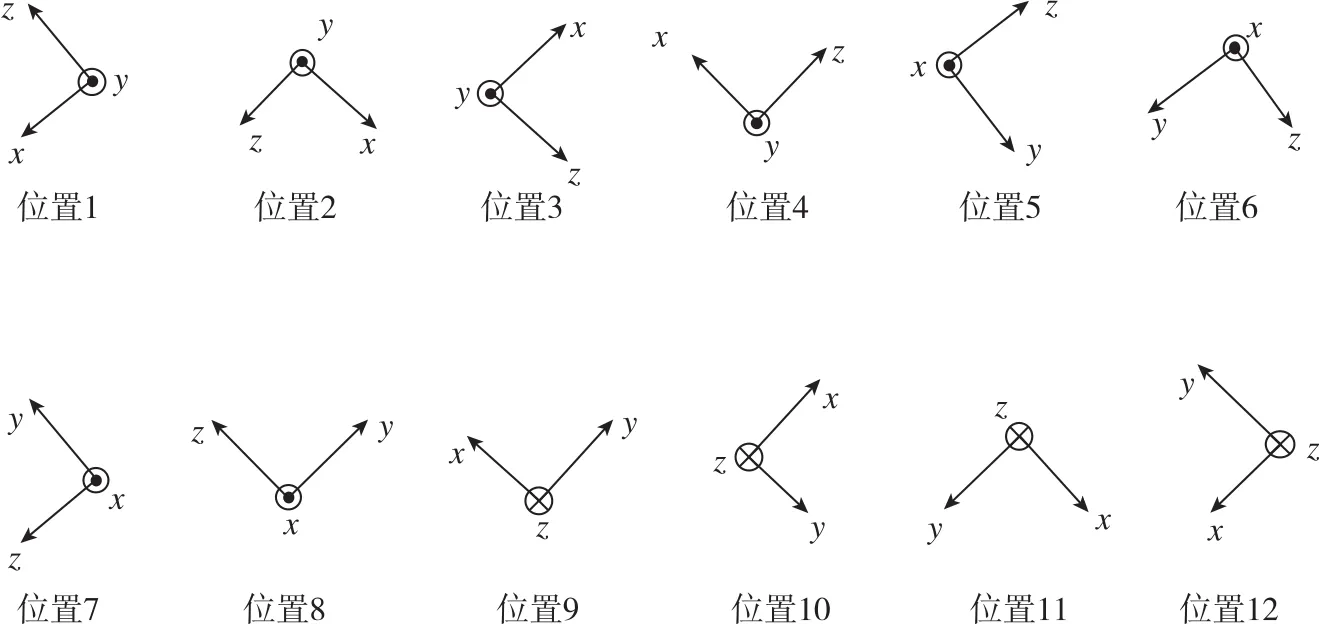
图3 系统级标定实验倾斜12位置编排Fig.3 Twelve tilt positions in systematic calibration experiments

图2、图3给出了基于IMU的位置编排。图2中，每个位置分别给出了当前IMU轴系的方位、旋转轴以及旋转方向与角度，k＝0，1，2，…，n，本文实验选择k＝0。图3则给出了估计加速度计振摆误差的12个倾斜位置，符号⊗代表垂直向内，符号☉代表垂直向外。

基于上述的位置编排，区分开倾斜或者非倾斜位置，仅在静态数据段以速度为零作为观测量进行滤波估计，得到加速度计的各项误差参数的估计值，开展了三组重复性实验，结果如表3～表7所示。

表3 加速度计组件标度因数标定结果Table 3 Calibration results of accelerometer assembly scale factor

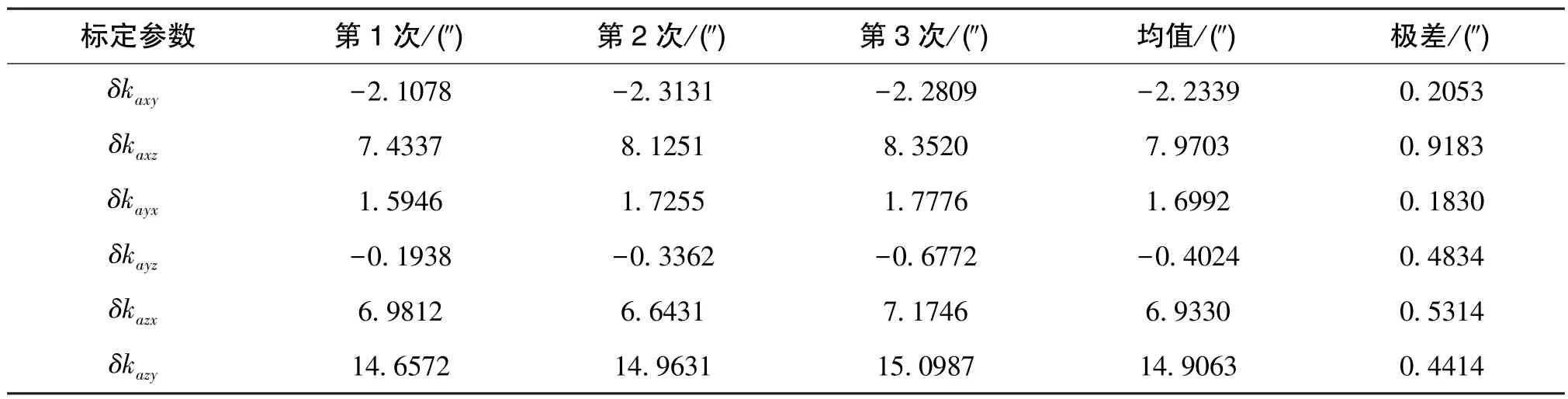
表4 加速度计组件安装误差标定结果Table 4 Calibration results of accelerometer assembly installation error

表5 加速度计组件二次项误差标定结果Table 5 Calibration results of accelerometer assembly quadratic term error

表6 加速度计组件零偏标定结果Table 6 Calibration results of accelerometer assembly bias

表3～表7给出了三次重复性实验中所有误差参数的估计值：标度因数误差的极差约为7×10－6；安装误差的极差约为0.9″，二次项误差的极差约为9μg／g2，零偏的极差为2.4μg，振摆误差的极差约为12μg／g2。从统计结果中可以看出，基于ST-EKF与滤波增益约束的系统级标定算法对误差参数的估计具有较好的重复性。

在23＋12位置编排中，分别选择6个倾斜位置与6个非倾斜位置来开展验证实验。

表8和图4给出了IMU倾斜时不同标定模型下的重力残差模值统计结果和示意图。

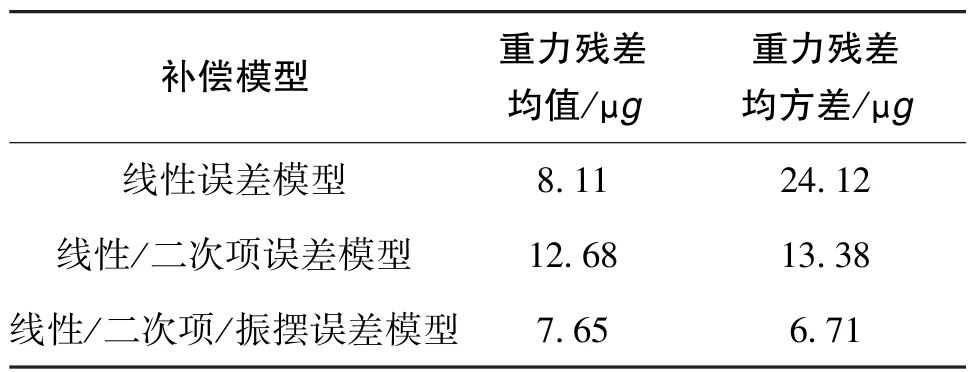
表8 IMU倾斜时不同标定模型下的重力残差模值统计结果Table 8 Statistical results of gravity residual modulus under different calibration models when IMU tilts

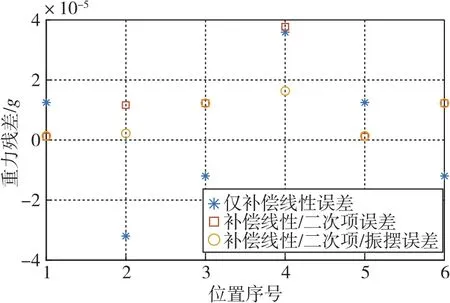
图4 IMU倾斜时不同标定模型下的重力残差模值图Fig.4 Diagram of gravity residual modulus under different calibration models when IMU tilts

由表8和图4可知，标定了非线性误差项的加速度计组件具有更高的输出精度。尤其，当对加速度计组件的振摆误差进行标定后，在大水平倾角下与对加速度计补偿线性／二次项误差相比，重力残差模值的均值从12.68μg减小到7.65μg，均方差从13.38μg减小到6.71μg；而与仅补偿线性误差相比，重力残差模值的均值从8.11μg减小到7.65μg， 均方差从24.12μg减小到6.71μg。

表9和图5给出了IMU非倾斜时不同标定模型下的重力残差模值统计结果和示意图。

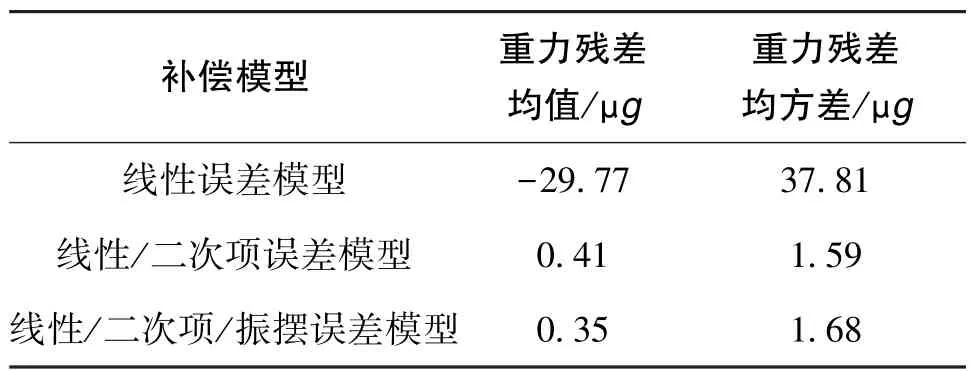
表9 IMU非倾斜时不同标定模型下的重力残差模值统计结果Table 9 Statistical results of gravity residual modulus under different calibration models when IMU is not tilted

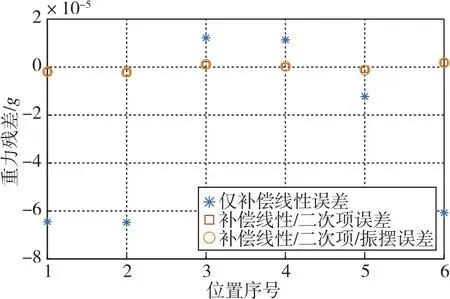
图5 IMU非倾斜时不同标定模型下的重力残差模值图Fig.5 Diagram of gravity residual modulus under different calibration models when IMU is not tilted

由表9和图5可知，补偿线性／二次项误差与补偿线性／二次项／振摆误差的重力残差模值的均值与均方差基本一致，且都要优于仅补偿线性误差的情况。

表10和图6给出了基于ST-EKF与EKF两种不同系统级标定算法对误差参数估计的统计结果和示意图。

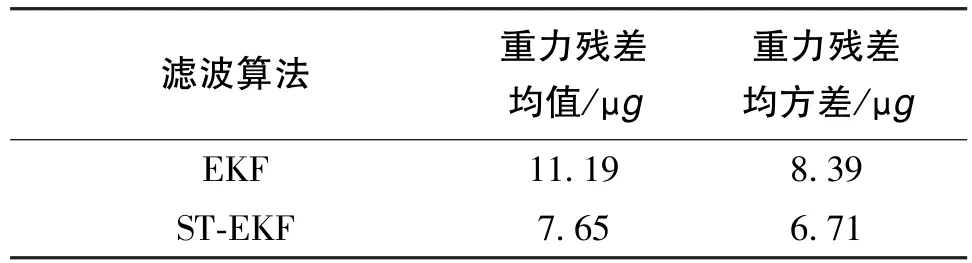
表10 基于EKF与ST-EKF系统级标定重力残差模值的统计结果对比Table 10 Comparison of statistical results based on EKF and ST-EKF systematic calibration gravity residual modulus

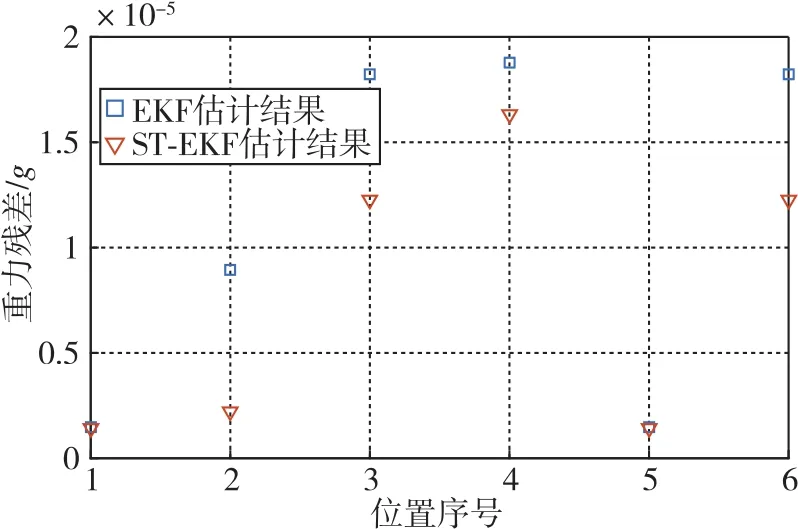
图6 EKF与ST-EKF系统级标定重力残差模值对比图Fig.6 Comparison of gravity residual modulus in systematic calibration based on EKF and ST-EKF

由表10和图6可知，基于ST-EKF的系统级标定算法对误差参数的估计具有更高的精度。相比于基于EKF的系统级标定算法，基于ST-EKF的系统级标定算法估计出来的参数补偿加速度计后，其重力残差模值的均值为 7.65μg，均方差为6.71μg，而基于EKF的系统级标定算法其值分别为 11.39μg和 8.39μg。

表11和图7给出了有无滤波增益约束的基于ST-EKF系统级标定算法对误差参数估计的统计结果和示意图。

表11 有无滤波增益约束的ST-EKF系统级标定重力残差模值的统计结果对比Table 11 Comparison of statistical results based on ST-EKF systematic calibration gravity residual modulus with and without filter gain constraint

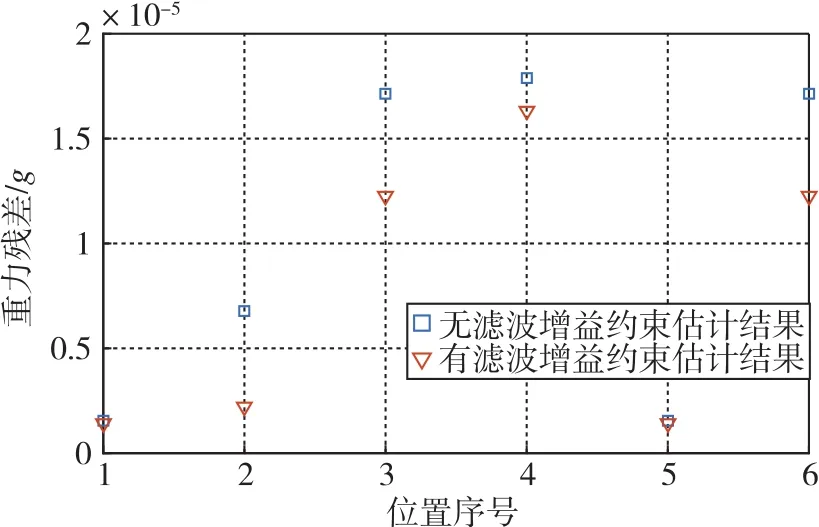
图7 有无滤波增益约束的ST-EKF系统级标定重力残差模值对比图Fig.7 Comparison of gravity residual modulus in systematic calibration based on ST-EKF with and without filter gain constraint

由表11和图7可知，有无滤波增益约束的基于ST-EKF的系统级标定算法对线性误差、二次项误差、振摆误差进行估计，并对加速度计补偿后在大水平倾角下的重力残差模值进行对比，结果表明：有滤波增益约束的基于ST-EKF的系统级标定算法标定精度更高。在有滤波增益约束下，加速度计经过补偿后，重力残差模值的均值为7.65μg，均方差为6.71μg；而在增益不进行约束的情况下，其均值为10.34μg，均方差为7.96μg。

图8为姿态角变化曲线，图9、图10为不同标定模型下北向和东向位置误差对比曲线。

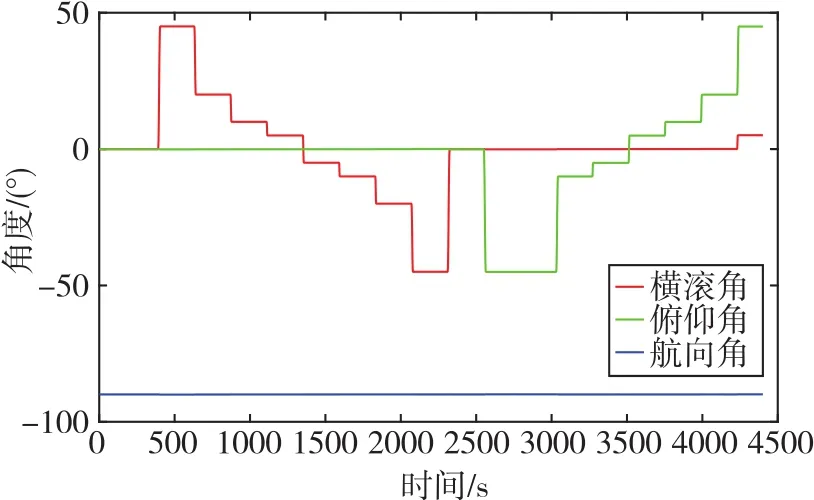
图8 姿态角变化曲线Fig.8 Change curves of attitude angles

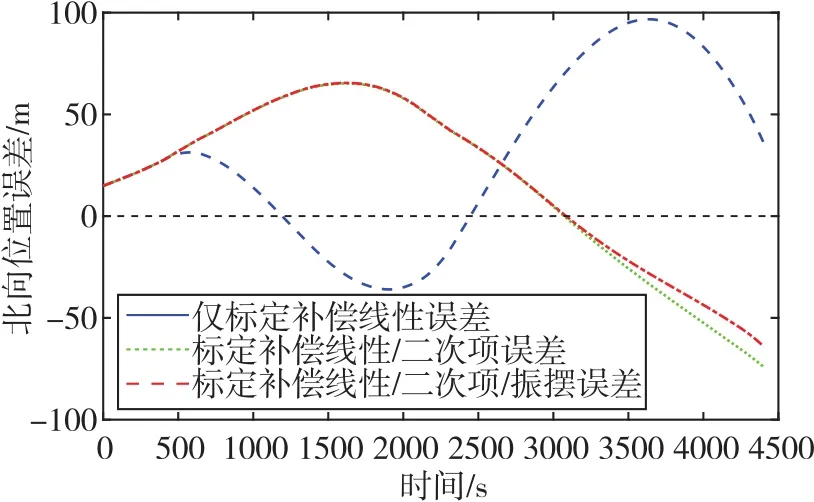
图9 不同标定模型下北向位置误差对比曲线Fig.9 Comparison curves of north position error under different calibration models

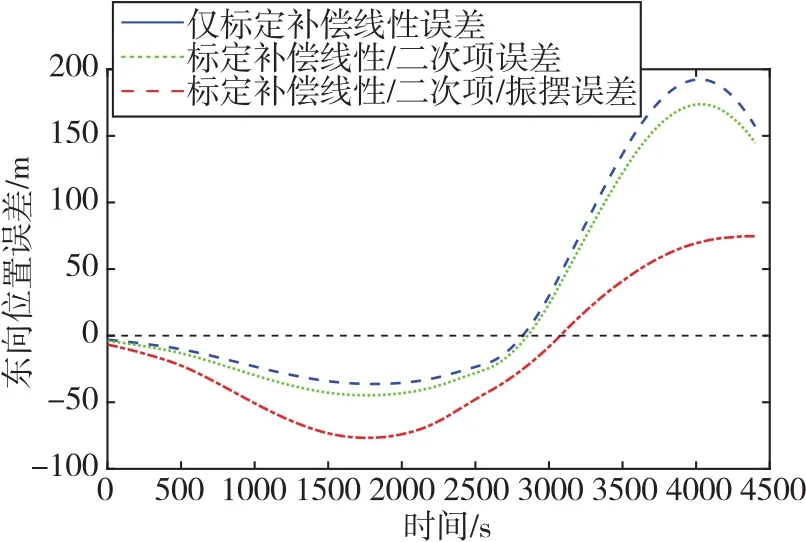
图10 不同标定模型下东向位置误差对比曲线Fig.10 Comparison curves of east position error under different calibration models

由图8～图10可知，当惯导系统处于大水平倾角时，将基于ST-EKF与滤波增益约束系统级标定算法估计出的各项误差参数通过线性／二次项／振摆误差标定模型补偿加速度计的输出后，其北向和东向位置的最大定位误差得到减少。具体而言，对比仅标定线性误差，东向与北向最大位置误差分别从 192.40m、96.72m 减小到 74.64m、65.44m；对比标定线性／二次项误差，东向与北向最大位置误差则分别由173.70m、65.49m减少到74.64m、65.44m，结果证明了在大水平倾角变化下标定二次项误差与振摆误差对提高惯导系统导航精度的必要性以及论文所提算法的有效性。

3 结论

随着对导航定位、测姿精度的要求越来越高，对惯性器件误差来源与标定算法的研究也越来越深入。在高精度标定中，当惯导系统处于倾斜位置时，加速度计二次项误差和振摆误差对惯导系统导航精度的影响不容忽略，本文因此建立了包括二次项误差和振摆误差在内的加速度计组件误差模型，并利用ST-EKF和滤波增益约束解决了状态转移矩阵计算不准确以及弱可观非线性误差项估计不准的问题，提出了一种基于ST-EKF与滤波增益约束的系统级标定算法，并通过重复性实验与对比实验验证了该算法在大水平倾角变化下的精度优势。最后，在大水平倾角变化下给出了线性、线性／二次项与线性／二次项／振摆误差标定模型下的东向与北向位置误差变化曲线，曲线表明经过线性／二次项／振摆误差模型补偿后的惯导系统具有更高的导航精度。