Buck 芯片缓冲电路设计的仿真分析与应用*
叶丰华,刘 昊,康 磊,蔡文波
(浪潮电子信息产业股份有限公司 浪潮高效能服务器和存储技术国家重点实验室,北京 100086)
0 引言
Buck 芯片工作的基本原理是将高输入电压斩波成具有一定占空比的周期脉冲,之后再通过LC 滤波器将周期脉冲整合成稳定的低压直流电[1-3]。
传导高压脉冲信号的位置称为Phase 点,常用Buck电源的典型参数为开关频率500 kHz,输入电压12 V。Phase 点在500 kHz,0 V~12 V 脉冲的作用下,成为了一个不可忽略的噪声源。
为了降低开关损耗,当前开关电源的MOSFET 开关速度非常快,即Phase 点波形的上升沿和下降沿的斜率很高。芯片内的寄生电感(ESL)在这样的激励下能够在Phase 点产生很大的过冲 (Overshoot)[4-5],Phase 点过高的Overshoot 会超过下管MOSFET 的耐压值,造成MOSFET过压损坏[6-8],使用缓冲电路可以削弱过冲对电路器件的负面影响。
本文通过对缓冲电路的缓冲效果进行比较分析,结合Buck 芯片中不同的缓冲方法下测得的电源效率,在仿真结果的辅助下评价两种缓冲方式的性能,探究缓冲电路的设计技巧,作为指导Buck 芯片缓冲电路设计的方法。
1 Buck 开关电源中缓冲电路的设计
为Phase 点到GND 设置缓冲吸收电路可以吸收Phase波形中的高频噪声,降低电压过冲和电磁辐射[9]。使用缓冲电路延缓开关速度,同样能够起到抑制Phase 点电压过冲的作用[10]。
1.1 Buck 开关电源原理
Buck 开关电源的基本原理如图1 所示。控制IC 分别控制Q1、Q2 两个MOSFET 的开关,当Q1 导通Q2 断开时,Vin通过导通的Q1 将能量传输到输出电感L,输出电容C 和负载。当Q1 断开Q2 导通时,因为电感和电容当中储存了能量,且因为电感的惯性不能允许电流的突变,会维持向负载端供电的状态,将电感中储存的能量传递到负载,Q2 此时起到续流通路的作用[11]。

图1 Buck 型变换器原理示意图
图1 中共有两处应用了缓冲电路,SW 点(即Phase 点)到BOOST 的RC,和SW 点到GND 的RC。
1.2 SW-GND 缓冲电路设计
Buck 开关电源的Phase 波形出现过冲和震荡的直接原因是寄生参数,如ESL(寄生电感)、等效电阻、电容等,这些参数无法避免。
图2 中Llp(Hi)是上管MOSFET Q1 的引线电感,Rds(on)是上管Q1 导通时的电阻值。Llp(lo)是下管MOSFET Q2 引线电感,Coss是下管Q2 的DS 两级之间的等效电容,当Coss被充电,其上的电压为
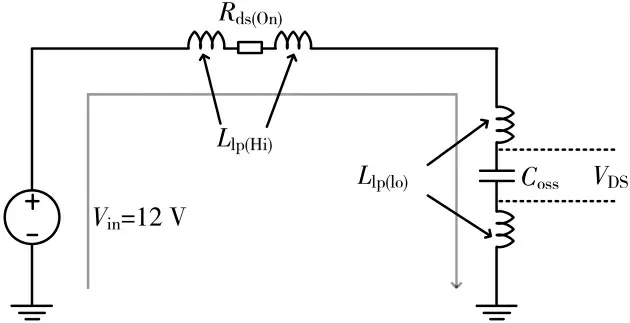
图2 等效寄生参数电路
当上管导通时,等效于Vin通过图2 的通路对下管Q2的寄生电容Coss充电从而产生VDS的波形,VDS就是Phase点的波形。
由于图2 的通路中存在电感电容和电阻,因此当上管导通时,即便Coss已经上升至Vin,电感因为惯性还会继续给Coss充电,形成过冲。
研究上管导通下管断开的瞬间,此时由于Q1 突然的导通,导致回路上寄生电感储存了能量,根据能量守恒定理,电感中储存的能量转移到电容中,得到:

式(1)中iqrr是通过下管MOSFET 的最大电流,vp是下管MOSFET 上的最大波动电压,求vp的表达式叠加基准输入电压得到:

其中VPK是过冲电压的最大值,Vin是输入电压的大小,输入电压叠加最大波动电压得到最大过冲电压。iqrr是MOSFET 体二极管的反向恢复电流,这个电流是下管MOSFET 寄生二极管反转过程中的最大值电流,由此确定了SW 点波形的最大过冲。
式(2)中的寄生电感Llp(Hi)和电流iqrr通常在芯片内进行补偿。芯片外,可以在SW 点和GND 之间加入一个电容Cf,该电容Cf和Coss形成并联的关系,能够等效地增加Coss的大小,从而也能够抑制最大过冲的峰值。由此确定,SW 到GND 加入电容Cf的做法能够优化过冲电压。
被吸收的能量不会损耗在抗性元件上,而是耗散在电阻上,为了将电容吸收的过冲能量耗散,并且易于控制缓冲器的整体阻抗,则在Cf通路上再串联一个Rf,最终的做法是在SW 和GND 之间加入一个RC 串联电路。
站在频域的角度分析Cf电容的选型,电容滤波的本质基于电容的频域阻抗曲线,常在某一频率达到低至10 mΩ~100 mΩ 的阻抗,这样的低阻抗能够用于吸收特定频段的噪声[13]。
根据电容频域阻抗公式结合Rf得到缓冲电路阻抗:

其中Zf是整个缓冲电路的频域阻抗,f 是频率。
去除所有的缓冲设计,测试phase 波形中的噪声振荡频率f,为滤除该噪声令该频段下电容阻抗小于100 mΩ,可供选择的电容容值即可计算得到:

联系式(4)知,足够大的Cf能够有效滤除噪声,但是不能太过偏离上式所计算出的电容值,否则滤波的频段会产生偏差。
虽然使用缓冲电路能够滤除噪声降低过冲,但本质上是在消耗功率,SW-GND 缓冲电路必然会在一定程度上影响开关电源的效率,这在对于开关电源效率要求甚高的应用场合提出了挑战,研发人员需要既达到缓冲性能的要求,又不对效率造成明显的损失。
Vin通过输入点到SW 点的电感Llp(Hi)对下管MOSFET的DS 电容Coss充电,后级电路是与之并联的缓冲电路Rf和Cf。面对上管MOSFET 的突然打开,上述电路会产生阶跃响应,Cf上的电压UCf将会产生变化,通过Rf的部分将会产生功耗损失:

其中Q 是缓冲电路产生的功耗,t 是计时时间,该缓冲电路产生的功率损失与Cf、Rf的大小正相关。
1.3 BOOST 缓冲电路设计
Buck 芯片驱动原理如图3 所示。
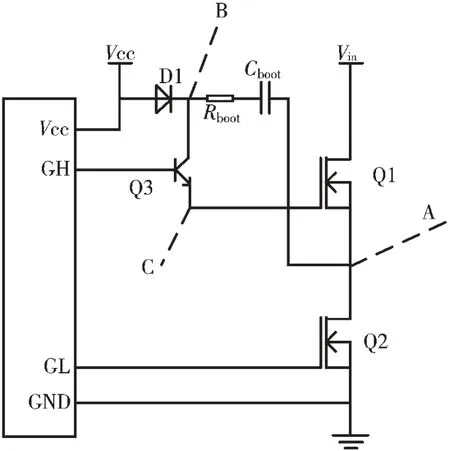
图3 Buck 芯片驱动电路简图
GH 和GL 发出的驱动信号分别驱动Q1 和Q2,输出信号GH 经过射极跟随器后驱动Q1。射极跟随器的工作电源由自举电路RC 提供,当下部开关Q2 导通时,通过D1 给Cboot充上电压Vcc。当上部开关Q1 导通时,B 点和A 点的电压都上升,但是压差VBA保持不变,被抬升的B 点电压将成为射极跟随器的工作电压[14-15]。
射极跟随器导通后,相当于Cboot对Q1 的GS 之间的寄生电容Cgsh充电,其上的电压为vgsh,用Vboot表示Cboot上的电压,则Q1 导通的过程相当于Cboot中的初始电压Vboot经过Rboot向Cgsh充电的过程,使得vgsh达到UGS(th)之后MOSFET 即可导通。
当Cboot远大于Cgsh时,Cgsh的充电方程满足:

MOSFET 的漏极电流iD和GS 之间电压vgsh的关系式如下:

其中IDO是vgsh=2UGS(th)时的iD,该方程可以体现一个MOSFET 开启快慢,Phase 波形的最大波动vp和iD的关系是:
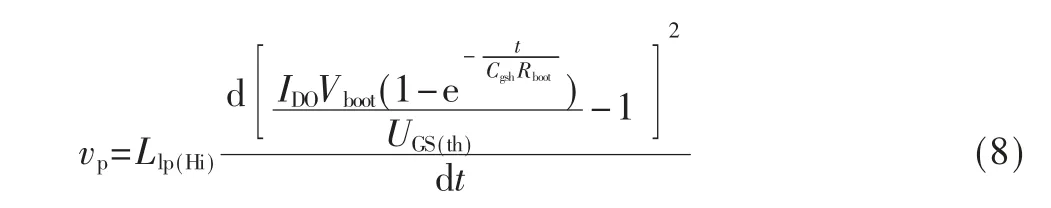
所以更改Rboot可以通过改变MOSFET 的开启速度达到限制过冲的效果。
当不满足Cboot远大于Cgsh时,vgsh最终稳定电压是:

只有当Cboot远大于Cgsh时,式(9)才成立,此时Vboot近似于不变,Cboot可近似为理想电压源。增大Cboot放电的时间常数,可以保证上管导通时间内Vboot只有较小的波动,但在实际应用中,Vboot总会产生一定的跌落,为了确保电压跌落不影响MOSFET 正常导通,工程上认为Vboot波动不可超过5%。根据式(10):

式中iBST是Cboot的放电电流,芯片数据手册中可以查找到其最大值;Vboot(D)是在上管导通时间内Vboot的变化;ton是指上管导通的时间。若已知Buck 电源的占空比D,初始驱动电压Vcc,开关频率f,则可以计算出Cboot的最小值:

为了保证当上管断开,下管导通时,Vcc能够快速完成对Cboot的充电,RbootCboot的时间常数τ 不宜过大,工程上认为至少要使Cboot在下管导通的10%时间内完成充电,利用式(12)可以求出Cboot的最大值:

MOSFET 在开关过程中会产生开关损耗,其根本在于每次MOSFET 的开关变换都不可避免地存在V-I 交叠。MOSFET 的每个极间电容在每个开关过程中需要充放电,以完成整个开关过程,所以V-I 交叠会持续一定的时间。当电容越大,充电时间就会增大,MOSFET 开启速度更慢,V-I 交叠时间越长,结果导致开关损耗变大,可以计算MOSFET 开启至V-I 交叠完成之前的时间[16]表示如下:

其中,Cgdh是MOSFET 的GD 两极之间的电容,I0是负载电流,g 是MOSFET 的跨导。在其他条件保持一致的情况下,当增大Rboot以减缓MOSFET 导通速度时,则必然增加V-I 交叠的时间,从而导致功率损耗的增加。
2 Buck 芯片缓冲电路的仿真
以常用系统电供电为例,Buck 变换器由控制器MPQ8633A 和外围元件组成,输入电压Vin为12 V,输出电压UO=0.6 V。Buck 型变换器仿真原理如图4 所示,原理图中的Rf和Cf即所述SW-GND 缓冲电路,RBST和CBST即所述BOOST 缓冲电路中的Rboot和Cboot。
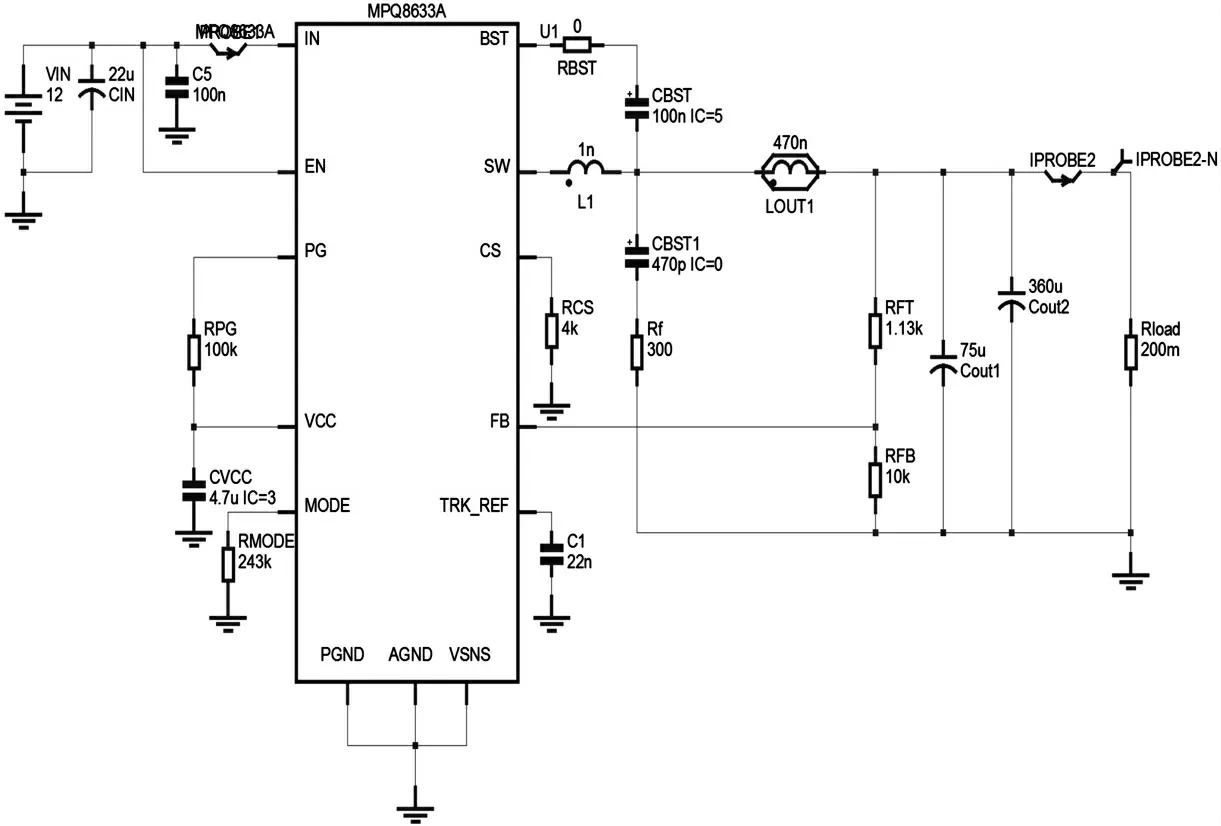
图4 Buck 型变换器仿真原理图
2.1 Buck 芯片SW-GND 缓冲电路仿真
不调整CBST和RBST,仿真观察不同Rf和Cf对于Phase波形的影响结果如图5 所示。
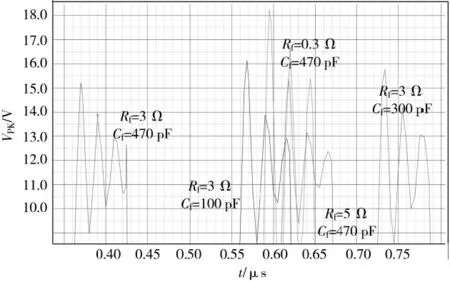
图5 SW-GND 缓冲电路仿真波
将仿真波形的最大过冲电压值进行统计,列表比较不同Rf和Cf对于Phase 波形的影响,如表1 所示。其中,VPK是指过冲最高电压值,eff 是指电源芯片的转换效率。
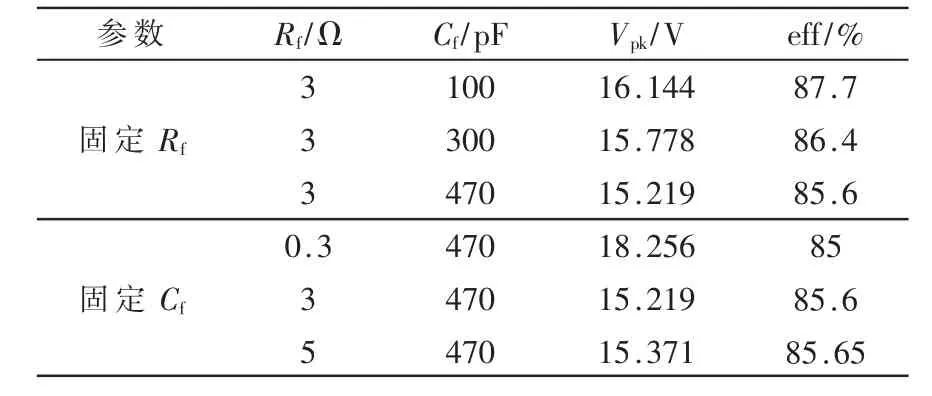
表1 SW-GND 缓冲电路仿真
2.2 Buck 芯片BOOST 缓冲电路仿真
不调整Rf和Cf,仿真观察不同RBST对于phase 波形过冲的影响,结果如图6 所示。
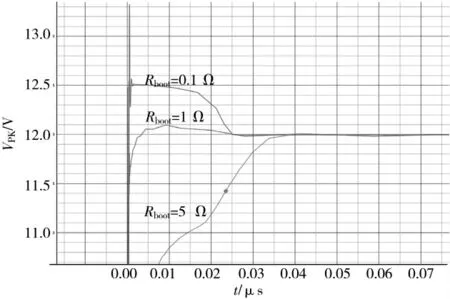
图6 BOOST 缓冲电路仿真波形
将仿真波形的最大过冲电压值进行统计,列表比较不同RBST 对于Phase 波形的影响,如表2 所示。

表2 BOOST 缓冲电路仿真
仿真数据说明,针对SW-GND 缓冲电路,Cf越大,越能够抑制波形的震荡过冲。Rf过小会使缓冲电路处于欠阻尼状态,延长震荡时间,增大过冲;Rf过大会增大滤波频域阻抗,降低滤波效果,也会增大过冲。缓冲电路能够影响电源的输出效率,由于Cf的变化决定了滤波频段,因此在更大程度上影响了效率,而Rf决定了针对目标频段的滤波效果。针对BOOST 缓冲电路,增大RBST的阻值能够延缓MOSFET 的驱动电压上升速率,从而影响MOSFET 的导通快慢,进而有效优化Phase 电压过冲。
总的来看,BOOST 缓冲电路能够更好地降低电压过冲,但却产生了不可接受的效率损失。
3 Buck 芯片缓冲电路的实验
在上述仿真电路参数完全对应的实际PCB 电路板上进行电源测试,根据仿真和前述理论计算,调整Buck电源中的对应器件,测试不同条件下的Phase 波形。
首先测试没有外部缓冲设计的Phase 波形,并测得效率P1,如图7 所示。
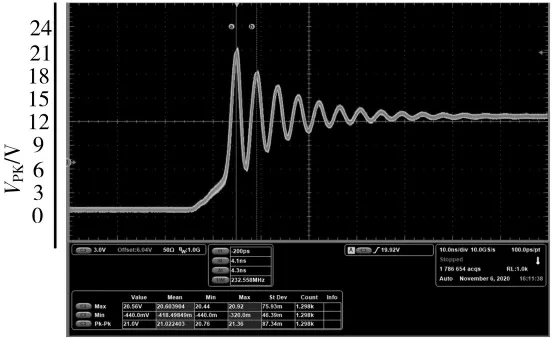
图7 无外部缓冲的Phase 波形
加入SW-GND 缓冲电路,Cf=470 pF,Rf=3 Ω,测得波形,并测得效率P2,如图8 所示。
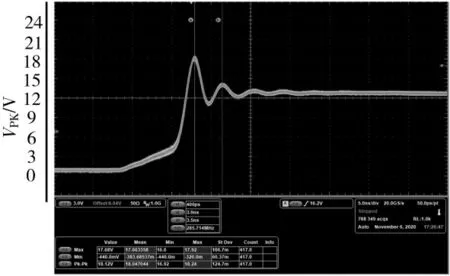
图8 SW-GND 缓冲的Phase 波形
使 用BOOST 缓冲电路,RBST=1 Ω,CBST=0.1 μF,测得波形,并测得效率P3,如图9 所示。
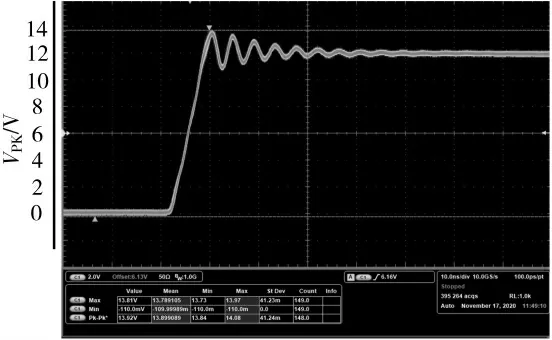
图9 BOOST 缓冲的Phase 波形1
更换为RBST=6 Ω,CBST=0.1 μF,测得效率P4,如图10所示。
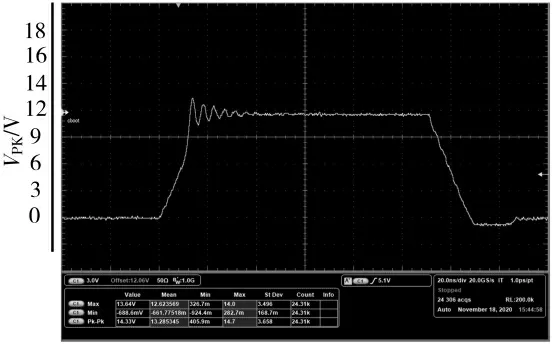
图10 BOOST 缓冲的Phase 波形2
将实测结果的电压过冲值和不同负载下的电源转换效率P1、P2、P3、P4列表,如表3 所示。
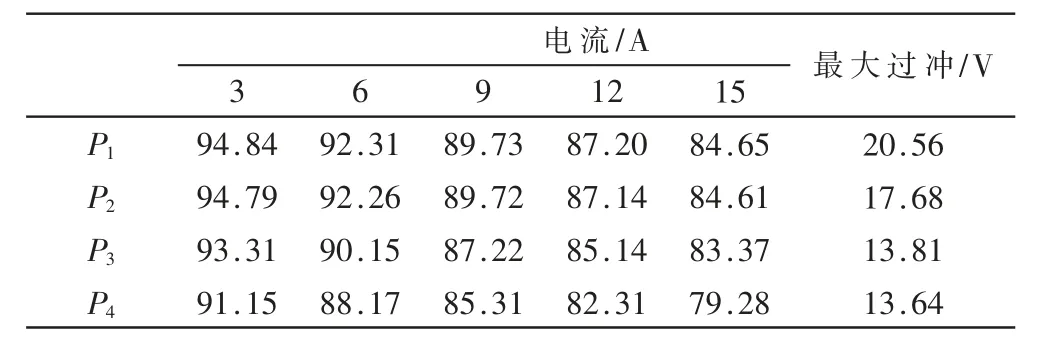
表3 实际电路板实测
根据实测结果分析,SW-GND 缓冲电路的能够在一定程度上削弱过冲,BOOST 缓冲电路抑制过冲的能力更强,但是缓冲电路势必造成效率的损失,如果MOSFET在降额设计下过冲仍然可接受,尽量不要增加任何的缓冲电路以获得最高的效率。当过冲不满足MOSFET 的降额设计时,将增加SW-GND 缓冲电路作为首选,BOOST缓冲电路作为次选,这与仿真结论是相符的。
4 结论
本文在理论上推导出两种缓冲电路的有效性和设计需求,并指出了每种缓冲电路的设计方法,基于缓冲电路对Buck 芯片的效率损失进行仿真分析,综合比较缓冲性能和效率之间的关系,最后通过实验验证仿真分析的可行性。
运用此方法的理论计算,以仿真作为参考依据权衡缓冲效果和效率损失之间的关系,可用于指导Buck 芯片的缓冲电路设计。

