轴对称非球面在位测量系统的研究

闫如忠，高 潮，王生泽，卢文科

（1.东华大学机械工程学院，上海 201620；2.纺织装备教育部工程研究中心，上海 201620;3.东华大学信息科学与技术学院，上海 201620）

0 引言

非球面零件广泛应用在军事、航天、医学等领域[1]，如美国加那利大型望远镜、欧洲共同体EURO主镜、法国兆焦耳激光系统。非球面零件作为各种光学设备中的核心器件，业界对其面型精度的要求越来越高，其检测技术已成为国内外的研究热点。英国伦敦大学研制的摆臂式非球面轮廓测量仪，测量口径可达1m,面形测量精度可达20nm；美国亚利桑那大学采用激光三角传感器实现了磨削阶段的非球面轮廓测量[2]；美国韦伯太空望远镜主镜在表面粗糙度达到10μm量级时,采用红外扫描来获得表面轮廓[3]。国内学者对此也开展了大量的研究工作，贾立德等[4]对摆臂式非球面轮廓测量仪的原理与技术进行了探讨；薛波等[5]采用工控微机作为上位机,用Visual C++开发工具设计了一套非球面测量系统，其测量行程为100mm～120mm，测量系统误差为5μm；范剑红等[6]采用工控机作为上位机，设计了光学非球面检验系统；郝群等[7]介绍了基于干涉法的非球面测量技术，但干涉法需制作特殊的补偿器，导致其通用性很差，且测量精度受到补偿器的影响较大；马志平等[8]提出了一种采用激光位移传感器做为测头的非球面在位检测系统。

离线测量存在二次装甲定位基准不重合误差、无法实时反应工件加工情况等缺点［9］，在线测量虽是动态测量但对传感器和环境的要求极高[10]，而在位测量不但能避免二次装甲定位基准不重合误差，还可实时观测加工结果，将误差反馈给设备补偿加工，从而提高制造精度[11]。由于非球面零件的非接触式测量方式对不同测量环境的通用性差，而接触式测量具有测量结果可靠、对环境适应性强等优点[12,13]。故针对应用广泛的轴对称非球面零件设计了一套接触式在位测量系统，通过运动控制卡和计算机通信对机床精密运动平台进行运动控制，同时数据采集卡通过采集机床各轴上的磁栅尺传感器信号得到测头触发时待测非球面零件上测点的空间坐标值，将所得各测点的坐标数据误差分离后进行曲面拟合并与设计曲面进行对比即可得到其面型误差。该系统测量过程直观，可靠性高。采用更新的软件开发平台，提高了测量效率，采用模块化的开发思想，使得系统的兼容性和可移植性好，引入手摇控制器使得控制过程更加简单方便。

1 测量原理

非球面有轴对称非球面和非轴对称非球面，而光学系统中的非球面大部分是轴对称的。轴对称非球面可用其子午截面的方程来表示[14]：

上式中z轴为旋转轴，C为顶点曲率，其值为1/R，R是曲线顶点处的曲率半径，K为二次曲线常数，其值为-e2，其中e为二次曲线偏心率。Ai为非球面系数，当其为0时，式(1)表示二次曲面，且二次曲面的形状和K值有一定的对应关系。

轴对称类非球面其曲面方程可由子午面（Ⅰ或Ⅱ）绕对称轴旋转一周得到，通常只需按一定的间隔测量其子午线上各点的坐标，进行曲线拟合，再通过与理论曲线进行对比即可得出其面型误差。

采用最小二乘法多项式曲线拟合算法对其子午线上的测量点数据进行拟合，该方法根据测量点数据（xi,zi）寻找其最合适的拟合曲线z=g(x)，以保证所有点到该曲线上对应点坐标的差值的平方和最小。即：

故需找到最佳的拟合曲线g(x)，使式(2)的值最小。其中g(x)可被n次多项式唯一线性表出，设其为：

通过确定n次多项式g(x)的各项系数a0，a1，…，an-1，an，使得式(4)的值最小。

当n=l时，g(x)为一次多项式，最小二乘拟合为直线拟合，如式(5)所示：

当n>1时，最小二乘法曲线拟合转化成多元函数求极值的问题。若其极值存在则其一阶偏导数必存在且其值为零，故有：

对(6)式进行整理有式(7)，式(8)和式(9)：

上式关于g(x)各项系数a0，a1，…，an-1，an的线性方程组可用矩阵的形式表示为：

当该矩阵为正定矩阵时，其有且仅有唯一解，由此可求出g(x)的各项系数，即可得到该组数据的最小二乘法多项式拟合曲线。

多项式g(x)的次数提高虽然可使测量点处的拟合精度提高，但可能使测量点处产生突变，出现龙格现象，且项数的增加会给加工和检验带来困难，故其次数一般小于六次。

2 误差分离

在位测量系统的主要精度评价指标为：测量精度（分辨率）和测量重复性精度。其精度受多种误差的影响，按照误差的性质可将其分为随机误差，系统误差和粗大误差。其中随机误差是由外界条件的随机变化产生的，它的出现没有规律性，随机误差虽然不可避免，但可采用多次测量取平均值的方法将其影响降低到最小。系统误差由机床系统误差和测量系统误差组成。机床误差有机床几何以及运动误差。测量系统误差有测头半径误差、位姿误差等。粗大误差是指在规定的测量条件下明现偏离真实值的测量值，其会导致测量结果严重失真，因此需要采取措施将其剔除。因机床工作平台采用气浮导轨，其各项性能都很优异，故重点对测量系统误差进行了分析。

2.1 测头半径补偿

在接触式测量中，得到的点的坐标为测头球心的位置坐标，必须对其进行半径补偿才能得到实际接触点的坐标。常用的补偿方法有三点共圆法、直接补偿法、曲线拟合法。

三点共圆法要求原始数据精度较高，一旦原始数据中存在粗大误差，将在后续补偿中被反复放大，产生错误的结果。直接补偿法有一定的局限性，工件的曲线方程必须已知，且对测量前的工件精度及测头分辨率要求较高。而曲线拟合法则没有那么苛刻的要求，且受到粗大误差的影响不大，故通常采用该方法进行测头半径补偿。

图1 轴对称非球面

2.2 位姿误差

由于测量坐标系和其原点与工件坐标系不重合，故会产生位姿误差，其会对测量结果的准确性产生影响。

图2 位姿误差模型

若以工件坐标系xyz为基准，测量坐标系x'轴、y'轴、z'轴分别转过α、β、Υ角度并将其原点平移T向量后与工件坐标系重合。则其旋转矩阵为：

若知道旋转矩阵R和平移向量T，则测量坐标系x'y'z'中的任意点都可以转换到工件坐标系xyz中，其变换公式如式(12)所示。

2.3 粗大误差

粗大误差具有严重偏离周边点数据的特点，因此，可先采用比较法直接对粗大误差点进行剔除，然后采用拉依达准则进行处理，找到其中的粗大误差点并对其进行剔除。拉依达准则在数据点满足正态分布时可用，首先分别计算出该组数据的算术平均值Z和标准差σ，若Zi-Z的绝对值大于3σ则Zi含有粗大误差，应将其剔除。重复这一过程，直到所有的粗大误差点被剔除。

3 试验平台建立

3.1 硬件系统

系统硬件部分如图3左部所示，由机床精密运动平台和计算机组成。机床精密运动平台关键器件包括三个方向的伺服电机、各轴磁栅尺传感器和Z轴搭载的接触式测头。测头选用DGC-6PG/A型LVDT测头。DGB-5B型电感测微仪是一种精度高，稳定性好，能够准确测出微小尺寸变化的精密仪器，配合DGC-6PG/A型测头可直接测出Z方向增量，测量精度可达0.1μm，重复测量误差小于0.07μm。

计算机主机中插入了运动控制卡和数据采集卡。通过运动控制卡和计算机通信，控制机床精密运动平台各轴上的伺服电机实现对平台运动的控制。当机床Z轴上的接触式测头发出触发信号时，由数据采集卡采集到此刻机床各轴上磁栅尺传感器的信号，并将其转化为测点的空间坐标值传给计算机保存，做进一步数据处理。

3.2 软件系统

该测量系统软件部分如图3右部所示，由在位数据采集模块和在位数据处理模块两部分组成。在位数据采集模块包括两个模块:运动控制模块和数据采集模块。通过对各个模块进行封装，使得软件的兼容性和可扩展性良好。

图3 测量系统总体方案

运动控制模块用来控制机床精密运动平台的运动。由于电机最后到达的位置和设置的位置之间会存在误差，采用增量式PID的模糊控制算法进行误差补偿，可精准控制三轴运动，并实时显示各轴误差情况。该模块中引入了手摇控制器使得控制过程更加简单方便。该手摇控制器有三个模块，x/y/z轴选模块、X1/X10/X100倍率放大模块、脉冲发生器模块。其中轴选和倍率模块为开关量，运动控制卡通过对对应端口高低电平的判别即可对各开关量的状态进行识别。脉冲发生器模块中需为其提供+5v电压，则当摇动手柄时，对应的2根引线之间会产生差分信号，通过对该信号的计数即可得到脉冲个数，再将其转化为需要移动的距离。

数据采集模块使计算机和数据采集卡建立通信实现对机床三轴上磁栅尺传感器位置信号的采集。该模块中集成了采样点路径规划、测点分布及其个数选取策略等功能。

在位数据处理模块主要功能是进行数据处理，包括测量数据的误差分离，非球面拟合，面型精度计算等。

4 试验验证

4.1 精度标定

通过标准球测量试验对该系统进行精度标定。如图4所示，选用的标准球为φ39.9965±0.0005mm，材料为不锈钢。找到标准球顶点后在xoz平面内将其设为坐标原点（0,0），沿x方向-2mm到2mm的范围内进行步长为0.05mm的逐点测量，得到的数据经过误差分离后对其进行最小二乘法圆形拟合得到的拟合圆如图5所示。其拟合半径为20.0004mm，圆心为（0.0000,-20.0004），与标准球的理论半径相比误差小于0.003mm，由此可知，该系统的测量精度较高。

图4 标准球测量

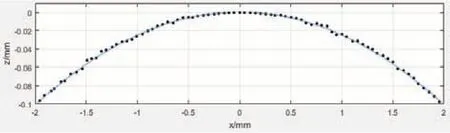
图5 标准球测量数据拟合

4.2 单点重复测量

如图6所示，打开测量软件，连接运动控制卡和数据采集卡，设置好相关参数，对非球面零件上的同一点进行40次重复测量，其结果如图7所示。图8为单点重复测量数据点偏差分布情况，由图可知，该测量系统单点重复测量标准偏差为0.00123mm，具有较好的稳定性。

图6 非球面零件测量

图7 单点重复测量试验数据

图8 单点重复测量偏差分布

4.3 子午线测量

对轴对称非球面零件的子午线进行在位测量试验，所用零件为折射率为1.61的非球面防辐射树脂镜片，直径70mm，中心厚度1.2mm。找到待测非球面零件顶点后沿X轴移动测头至零件边缘并在xoz平面内将该点的坐标值设为（-35,0），从x坐标为-35mm开始，测量间距为1mm，采样长度为70mm，共计70个点进行测量。对子午线的测量结果误差分离后，采用最小二乘法多项式拟合算法对其进行拟合，得到的结果如图9所示，可知其二次拟合和四次拟合相比残差相差不大，故取二次拟合，其拟合方程为：

图9 测量结果拟合曲线

4.4 面型测量

取该零件中心局部，采用弓字型测量轨迹，测量范围为x方向[-2,2]毫米，y方向[-2,2]毫米，x方向和y方向采样间距都为0.4mm，得到的拟合曲面如图10所示，其误差平方和为12.65μm，标准差为0.32μm，通过与其设计曲面对比即可知其面型误差。

图10 弓字形测量轨迹拟合曲面

对该零件相同局部上的每个相同测点采用海克斯康三坐标测量机进行测量，并对其测得的结果进行曲面拟合。为保证二者的测点尽可能一一对应，如图11所示，将测头沿着箭头方向以0.001mm步长缓慢移动，同时采集各点的坐标值。当测头到达平台边缘A点时，继续向前移动时其X方向坐标会有一个跳变，记下该跳变点的前一个测点的坐标值（XA,YA），对该点进行测头半径补偿后的坐标值（XA+r,YA）即为平台边缘点A的X、Y坐标值。对该点进行位姿校正后，在A点的基础上，将测头向X正方向移动60mm，向Y轴正方向移动30mm，到达镜片上B点，将该点作为镜片上的参考点。再从这点出发按照规划的轨迹进行测量。当在海克斯康三坐标测量机进行测量时，用同样的方法将测头沿着箭头方向以0.001mm步长缓慢移动，同时采集各点的坐标值，找到平台边缘A点的坐（XA’,YA’），因三坐标测量机已经进行过半径补偿，故只需在该点的基础上将测头向X正方向移动60mm，向Y轴正方向移动30mm，即可到达镜片上的参考点B点。再从这点出发按照相同的轨迹进行测量，从而保证机器上的测点和三坐标测量机上的测点尽可能一一对应。

图11 工件的测量

通过与该在位测量系统得到的测量结果进行对比，二者各测点坐标值分布如图12所示，二者拟合曲面z方向误差情况如图13所示，其最大值为0.00396mm，由此可知该在位测量系统得到的结果是可靠的。二者产生误差的原因可能如下：1）二者各测点未严格一一对应；2）二者测量环境不同；3）二者所用软件的数据处理精度不同；4）二者对工件的位姿误差处理方式不同等。后续将对其误差原因进行更加细致的分析，设法将该测量系统的误差降至最小。

图12 二者各测点坐标值对比

图13 二者拟合曲面Z方向误差

表4 不同规模下拣选路径和时间的对比

5 结语

非球面零件在众多精密器械中有着广泛的应用，而检测作为保证产品质量的关键环节显得尤其重要。针对非球面零件在制造过程中的面型精度检测完成了以下工作：

1）提出并开发了一套轴对称非球面零件在位测量系统。对该系统进行了误差分离，为测量结果的准确性提供了保障；

2）通过对标准球的测量，完成了该测量系统的精度标定，测量误差小于0.003mm。对该测量系统进行了单点重复测量试验，验证了其具有较好的稳定性；的问题。本文根据仓配一体化仓库的实际情况，建立TSP模型，分别用遗传（GA）和遗传模拟（GASA）算法对模型进行求解。在Matlab2012a中进行仿真，结果表明，在拣货路径方面，GA行走了505.8162m，GASA行走了502.7799m，路径节约了0.6%，在拣货时间方面，GA使用了442.0900s，GASA使用了439.7500s，时间节约了0.5%，故GASA比GA更适合求解这类问题。同时反映出，当拣货数量越多时，节约的拣货距离以及时间也越多，从而提高了仓库整体的拣货效率以及服务水平。

3）对轴对称非球面零件进行了在位测量试验，拟合出了其子午线方程；对其中心局部进行了弓字型轨迹测量试验，拟合出了其曲面形状，并与海克斯康三坐标测量机测得的结果进行了对比，二者z方向最大误差为0.00396mm；

4）该测量系统具有测量结果可靠，可降低非球面零件的加工成本，提高其加工效率等优点。