高速铁路车轮多边形对轨道动作用分析
李忠继 陈志贤 姚 力 杨吉忠 林红松
(中铁二院工程集团有限责任公司, 成都 610031)
目前,我国高速铁路无砟轨道的铺设里程已达3万多公里,形成了系统的设计、施工和运营维护理论技术体系,保证了高速铁路的高效安全运营。随着运营时间的增加,一些新问题也随之突显,其中车轮多边形磨耗就是较为突出的一个。运营中的高速列车车轮因连续磨耗,轮径不断减小,且在缩小的不同阶段发生不同程度的车轮多边形,某些阶段还十分严重。列车车轮非圆化磨耗会使轮轨间作用力显著增大,导致铁路车辆和轨道产生强烈的振动和噪声[1]。这给高速铁路设计,特别是未来更高速度等级高速铁路的设计带来了新的挑战。车轮多边形引起的轮轨作用效应是高速铁路设计,特别是轨道结构载荷研究和结构疲劳设计中应该重点考虑的问题。
国内外学者对车轮多边形问题开展了广泛的理论和试验研究,文献[2]建立了车辆轨道动力学模型,并引入了柔性轮对模型,考虑了轮对的弯曲变形,计算了车轮多边形磨耗对车辆系统动力学性能的影响。结果表明,车轮多边形对车辆运行平稳性指标影响不大,但会导致轮轨垂向力增大。文献[3]研究了高速车轮多边形对车辆横向运动稳定性的影响,结果显示车轮多边形会导致车辆横向蛇行失稳速度降低,严重恶化列车的运行品质,影响其横向稳定性。文献[4]通过建立刚柔耦合动力学模型,详细考虑了轮对的高频弹性振动模态,分析了车轮多边形磨耗对轮轴动应力的影响,结果表明,当车轮多边形磨耗激振频率和轮对固有频率接近时,轮轴动应力会显著增大。文献[5]将车轮多边形磨耗跟踪测试数据带入多刚体车辆轨道耦合动力学模型中进行计算,发现随着车轮多边形磨耗的加深,轮轨力逐渐增大,车轮多边形严重磨耗对轮轨力的影响超过了焊接接头不平顺对轮轨力的影响。文献[6] 研究了车轮多边形磨耗对车辆运行安全性能的影响,发现多个可能工况下的脱轨系数均在安全限度内,不会引起脱轨,虽然脱轨系数在安全限度内,但是对于高阶车轮多边形来说,往往会产生高频轮轨冲击载荷,导致转向架零部件发生损坏或者失效,同样也会对列车安全性 产生重要影响。文献[7] 以某城际高速列车在运行过程中发生转向架部件损坏事故为例,建立高速车辆-轨道耦合动力学模型和车轮多边形不平顺输入模型,计算分析列车运行速度、车轮多边形幅值及其阶数(或边数)等因素对轮轨垂向力的影响规律。结合现场高速车轮径跳的镟修期限统计和经验,以轮轨垂向动载荷限值为依据,考虑不同速度下1~23阶车轮多边形幅值的影响,初步建立高速车轮多边形状态下的安全镟修限值。分析安全限值曲线发现,当列车运行速度越快和车轮多边形阶次越高时,即使很小的车轮非圆化磨耗幅值也能导致轮轨力超限。
以上研究多围绕车轮多边形对车辆性能的影响和危害开展研究,但在车轮多边形对轨道结构动作用方面的研究较少。而在线路实际运用中,车轮多边形磨耗对轨道结构特别是对扣件、轨道板的危害已逐步显露。此外,随着我国高速铁路的发展,更高速度等级高速铁路的建造已经提上日程,在更高速条件下,多边形磨耗会对轨道结构产生怎么样的动作用、轨道结构设计中如何考虑多边形的动作影响,都是值得深入研究的问题。
本文对更高速条件下车轮多边形对轨道的动作用问题展开分析,为轨道结构设计列车载荷的取值提供理论支撑。利用多体动力学软件建立了车辆-轨道耦合模型,详细考虑了轨道扣件系统、道床结构,通过构造高阶车轮多边形,仿真分析不同运行速度下系统的动力响应,研究高阶多边形对轮轨动作用力的影响规律及影响幅度,确定车轮多边形条件下的轮轨力和扣件力取值。
1 车辆-轨道系统动力学模型
1.1 车辆系统动力学模型
以我国某型高速动车组为研究对象, 建立车辆系统动力学模型。动车组单节车辆包含1个车体、2个构架、4个轮对、8个轴箱,共计15个刚体。各刚体的自由度如表1所示,整车共计50个自由度。车辆系各刚体之间的关系及刚体和绝对坐标系间的关系,如图1所示,车辆系统动力学模型参数如表2所示。
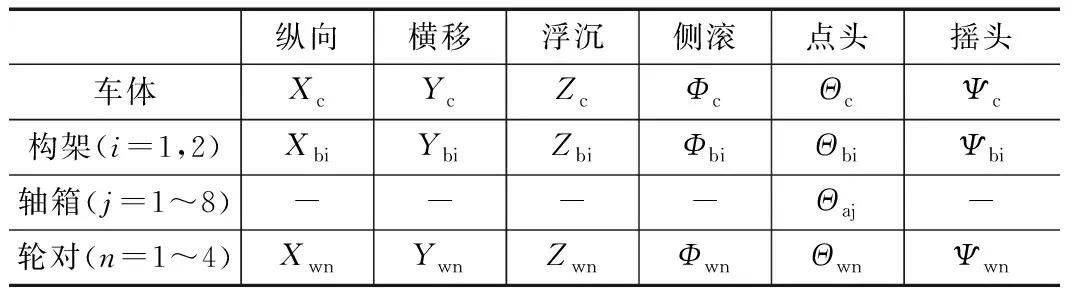
表1 某型高速列车动力学模型自由度表
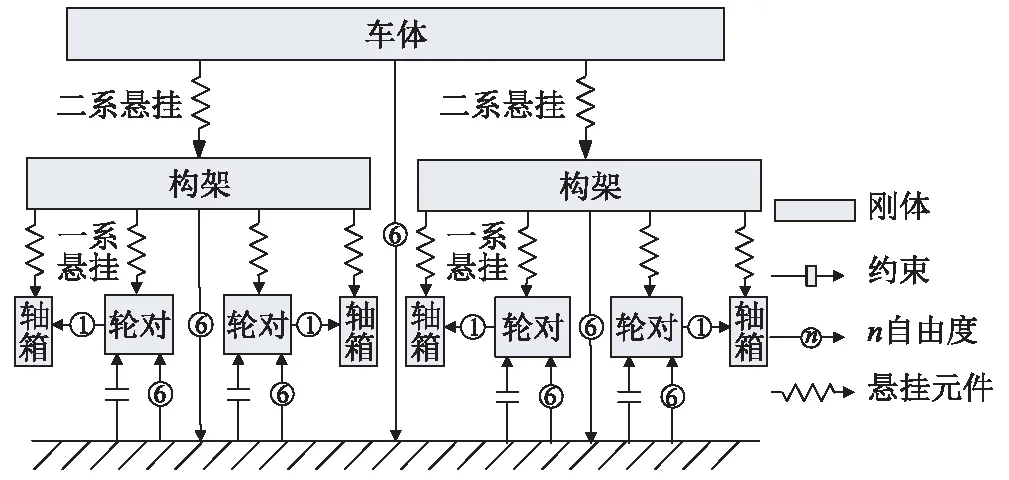
图1 车辆系统动力学拓扑结构图
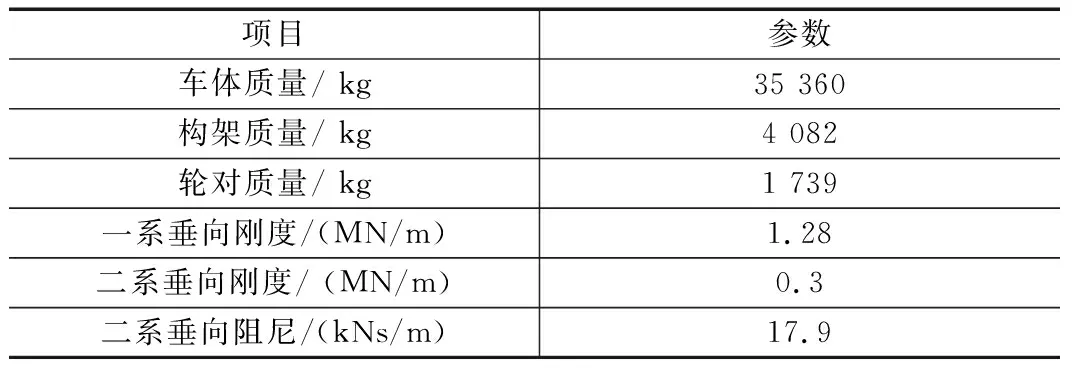
表2 车辆参数表
1.2 轨道系统模型
选取CRTSⅢ型无砟轨道作为研究对象,建立轨道结构动力学模型。CRTSⅢ型无砟轨道由60 kg/m钢轨、WJ-8扣件系统、轨道板、自密实混凝土、土工布隔离层和底座板组成。其中,轨道板与自密实混凝土浇筑在一起,在自密实混凝土与底座板之间设置土工布隔离层,底座板连接在下部基础结构(路基、桥梁)上[8]。
将钢轨考虑为弹性铁木辛科梁,通过扣件弹簧支撑于轨道板上,扣件为三向刚度阻尼弹簧力元。所建立的车辆轨道系统模型如图2所示[9],轨道参数取值如表3所示。
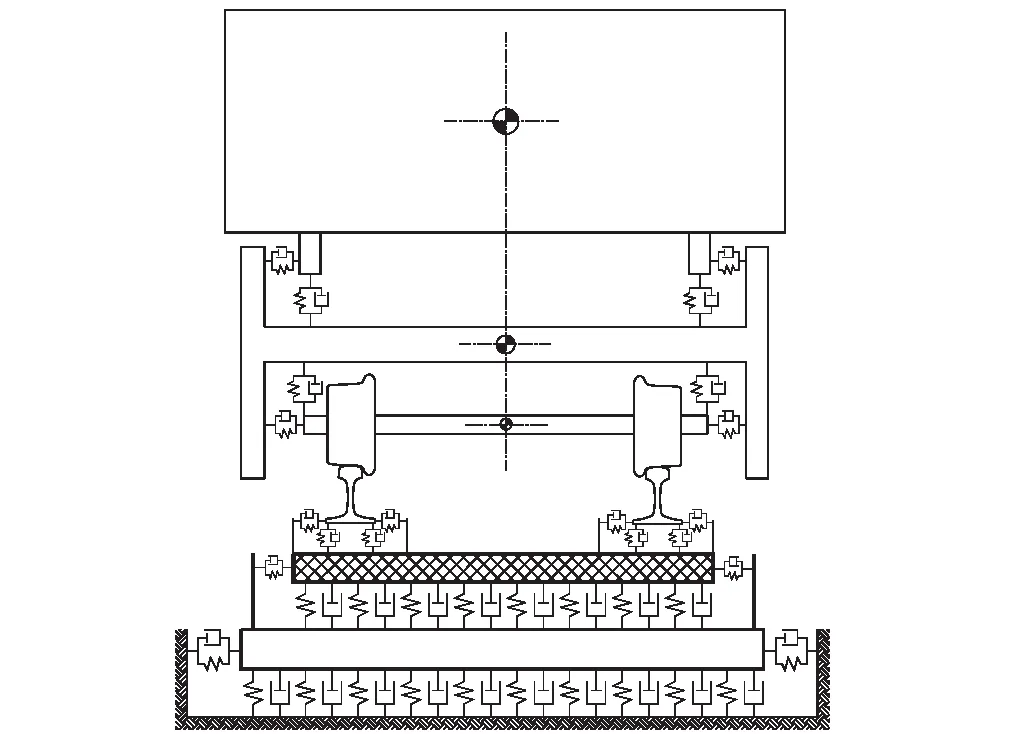
图2 车辆轨道结构模型图

表3 轨道参数表
2 车轮多边形模型
典型的车轮多边形如图3所示。车轮多边形属于一种谐波激扰。车轮圆周在轮轨不均匀磨耗等因素的作用下形成周期性轮径偏差。车轮多边形考虑为多阶谐波不圆顺,车轮圆周坐标(x,y)可表示为:
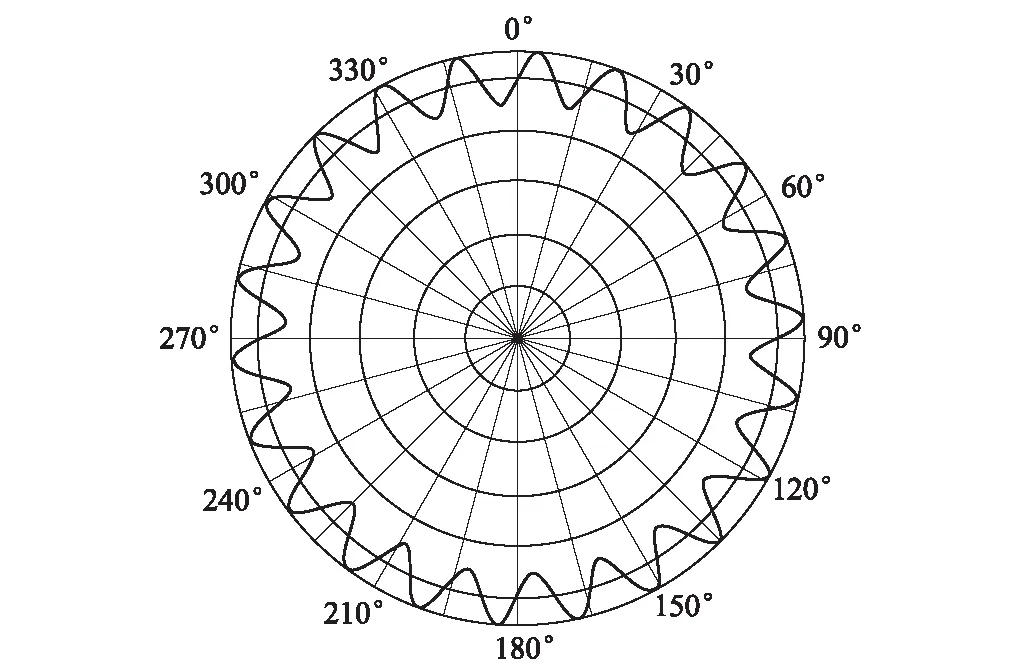
图3 车轮多边形图
(1)
式中:R——车轮滚动圆半径;
A——车轮多边形幅值;
N——车轮多边形阶数。
高速铁路运营中通常存在几阶、十几阶及二十几阶的多边形磨耗,甚至还存在多阶叠加的情况。为简化研究内容,明晰作用规律,本文以典型的20阶车轮多边形为例开展规律性研究。
3 仿真结果分析
3.1 轮轨垂向力
仿真计算速度范围为50~650 km/h,在车轮20阶 不圆条件下分析车辆轨道系统的动力作用,主要分析指标包括轮轨垂向力、轮轨力动载系数(轮轨垂向力与静轮重比值)、扣件垂向力及扣件力动载系数(扣件垂向力与扣件垂向静态力比值)等。一位车轮轮轨垂向力的作用历程如图4所示。从图4可以看出,在多边形车轮作用下,轮轨垂向力表现出显著的谐波特性,且在不同的运行速度下,空间波长和空间频率相等,均与车轮多边形波长相等。因此,随着速度变化,车轮多边形对轨道形成了一种谐波扫频作用。车轮多边形条件下,轮轨力随运行速度的变化过程如图5所示。

图4 车轮多边形条件下轮轨力历程(50~650 km/h)图
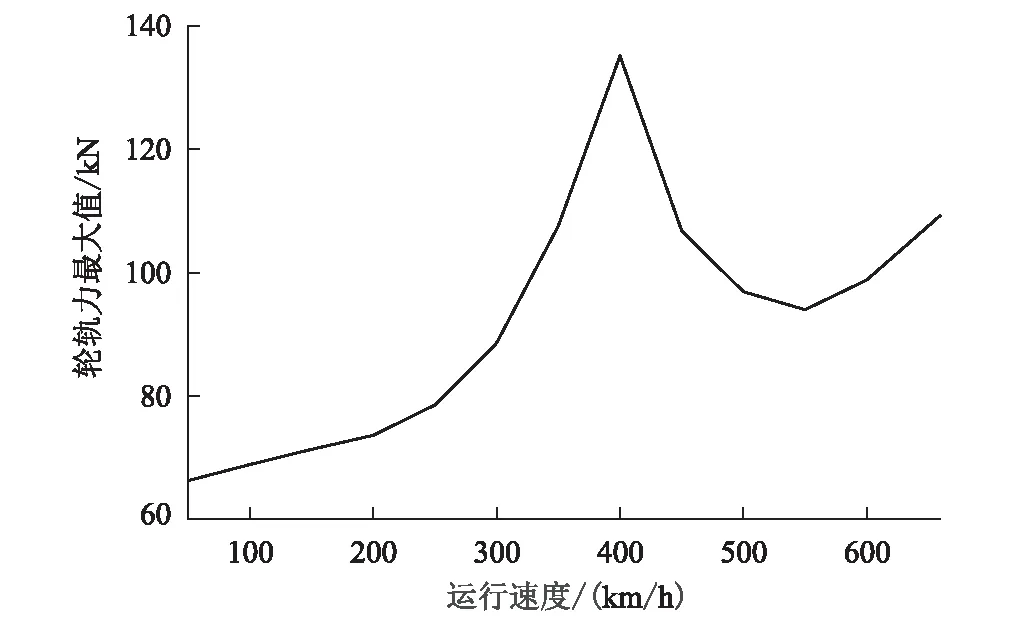
图5 不同速度下轮轨力最大值(幅值0.02 mm)图
从图5可以看出,随着列车运行速度的增大轮轨力最大值随之增加。但在350~450 km/h速度范围内出现了明显峰值,这是车轮多边形谐波作用与轮轨系统固有频域重叠,振动幅度增强的结果。峰值出现速度与多边形阶数、轮对质量、扣件力学参数及轨道结构相关。轮轨作用力增加对轨道结构及车辆结构均不利,在工程设计中应合理设置车辆及轨道系统参数,使峰值出现速度避开线路运营速度。
计算不同车速、不同车轮多边形幅值下轮轨垂向力最大值,结果如图6所示。从图6可以看出,在不同速度下轮轨力最大值均随车轮多边形幅值的增加而增大。轮轨力最大值受不圆幅值影响显著,当不圆幅值为0.02 mm时,轮轨力最大值为149 kN。当车轮多边形幅值为0.1 mm时,轮轨力最大值为291 kN。但峰值位置不受不圆幅值的影响,这也进一步表明峰值速度下出现了轮轨系统谐振现象。
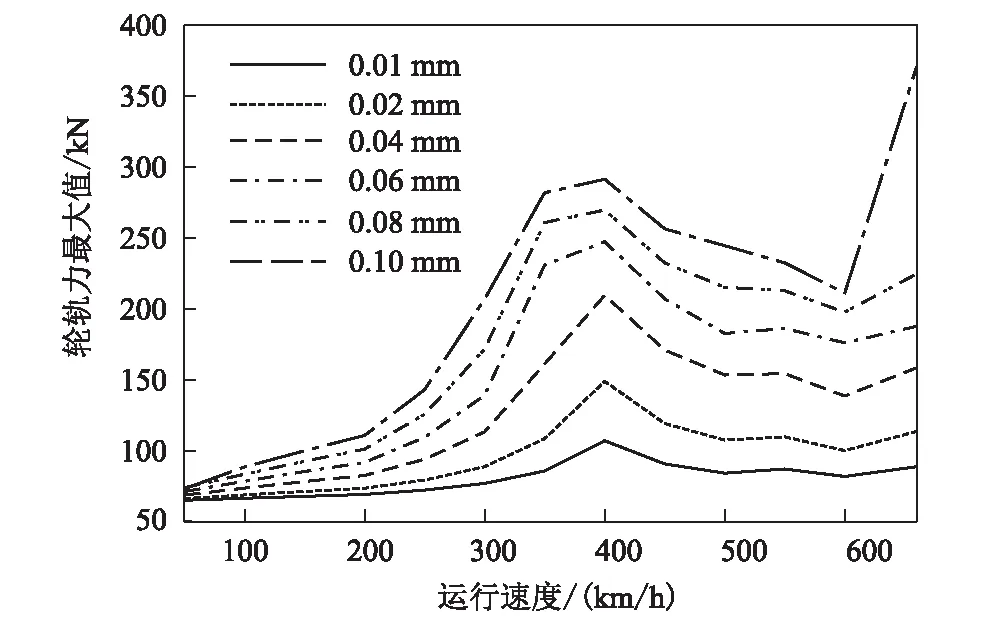
图6 不同不圆幅值下轮轨垂向力对比图
不同车速、不同车轮多边形条件下轮轨垂向力与静轮重比值如图7所示。从图7可以看出,车轮多边形幅值在0.01~0.1 mm范围内变化时,400 km/h条件下的轮轨力动静力比值在1.69~4.16范围内变化。
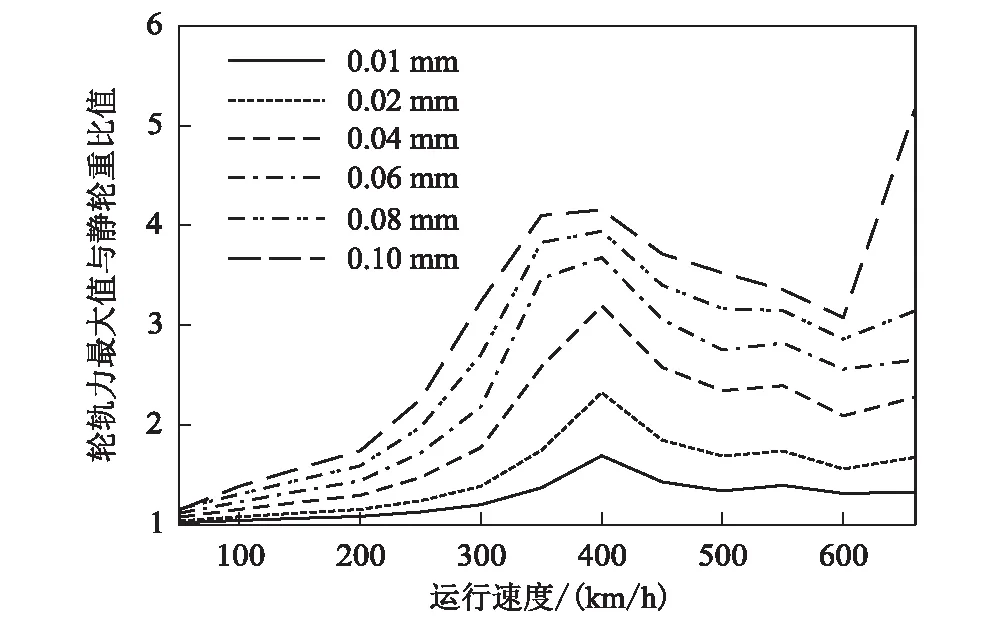
图7 不同不圆幅值下轮轨垂向力动静力比值图
3.2 扣件垂向力
扣件垂向力是轨道板受到的直接作用力,决定了轨道板的设计动荷载,因此应进一步分析车轮多边形条件下扣件垂向力的作用特点、最大值和变化规律。距离1位轮对初始状态8 m位置的扣件力变化过程如图8所示。从图8可以看出,随着车轮的逐渐靠近,扣件力逐渐增大,1位轮对驶过后,扣件力逐渐减小,当2位轮对经过时,扣件力再次增大。扣件力在准静态分量上伴有车轮多边形所诱发的高频波动。当前转向架通过时,两车轮间存在拍振现象,该拍振是引起轮轨力和扣件垂向力共振的主要原因。
车轮多边形条件下扣件力最大值随运行速度的变化过程如图9所示。从图9可以看出,扣件垂向力与轮轨垂向力随速度变化的规律相同。20阶 0.02 mm车轮多边形条件下,在350~450 km/h速度范围内同样出现了明显峰值, 为24.85 kN。车轮多边形幅值在0.01~0.1 mm范围内变化时扣件力的变化趋势如图10 所示。从图10可以看出,随着多边形幅值的增加,扣件力最大值也随之增加,但当车轮多边形幅值大于0.06 mm后,扣件力最大值幅度变化减小,最大值为31 kN。
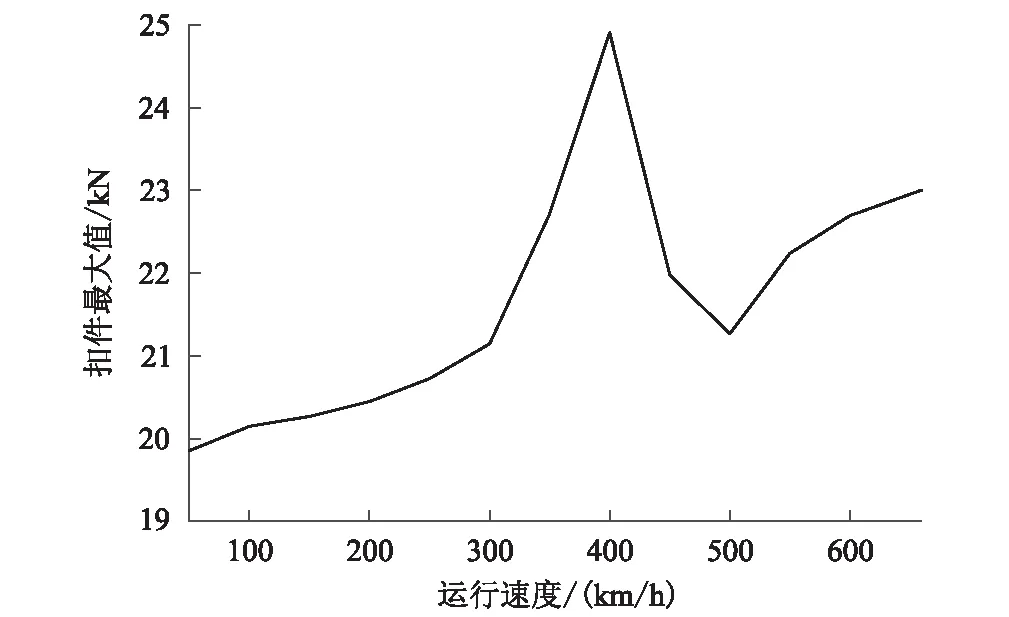
图9 不同速度下扣件垂向力最大值(幅值0.02 mm)图

图10 不同不圆幅值下扣件垂向力最大值图
不同车速、不同车轮多边形条件下轮轨垂向力与静轮重比值(即扣件力动静力比值)如图11所示。
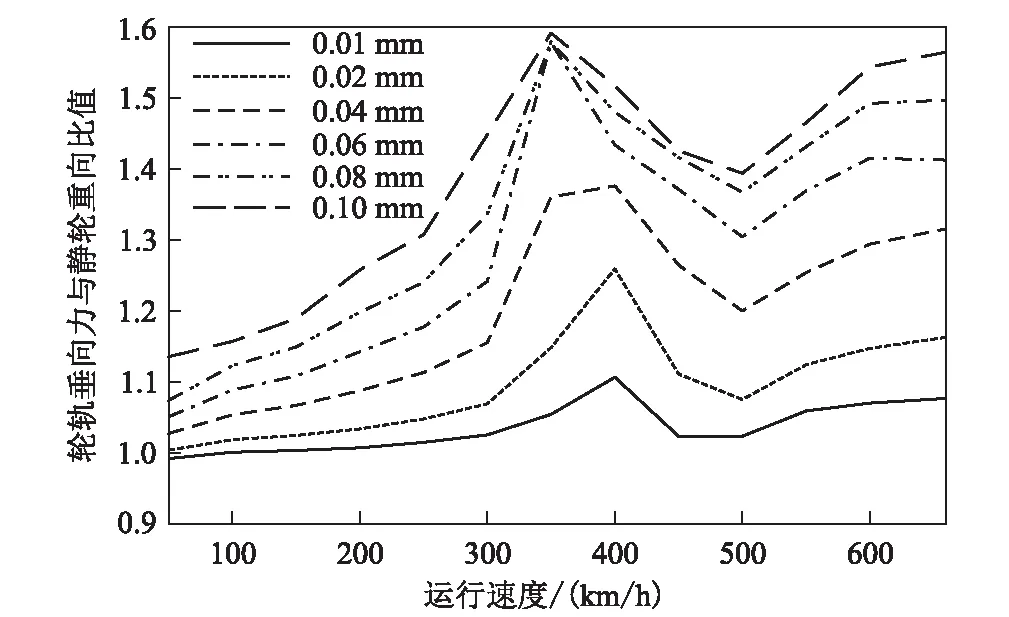
图11 不同不圆幅值下扣件力动静力比值图
从图11可以看出,车轮多边形幅值在0.01~0.1 mm范围内变化时,400 km/h速度下的轮轨垂向力与静轮重比值在1.11~1.59范围内变化。
4 结论及展望
本文通过数值模拟方法研究了车轮多边形条件下高速铁路的轮轨动作用特征。通过建立详细的车辆-轨道耦合模型,考虑轨道扣件系统、道床结构,仿真分析了20阶车轮多边形在不同车速下的轮轨动力响应,计算了轮轨垂向力及扣件垂向力,为更高速度下轨道载荷设计提供了理论及仿真依据,得出以下结论:
(1)车轮多边形对轨道结构的作用为谐波激励,激励空间波长与车轮多边形波长相同。随着运行速度的增加,多边形激励频率随之增加,对轨道结构形成扫频作用。对于本文所采用的模型参数,在350~450 km/h范围内,轮轨力和扣件力出现共振峰值,在工程设计中有必要开展系统参数研究使共振峰值避开此线路运营速度。
(2)轮轨力最大值随车轮多边形幅值的增加而增大。轮轨力最大值受不圆幅值影响显著,400 km/h速度条件下,当不圆幅值为0.02 mm时,轮轨力最大值为149 kN;当车轮多边形幅值为0.1 mm时,轮轨力最大值为291 kN。
(3)400 km/h速度条件下,车轮多边形幅值在0.01~0.1 mm范围内变化时,扣件力最大值为21.89~31.49 kN。
本文结论是在20阶车轮多边形条件下得出的,由于高速铁路不同列车在不同类型轨道、不同运行速度下会形成不同阶次的车轮多边形,其对轨道结构的动力作用也会有所区别,本文所研究的仅是其中一种工况,因此,在实际工程中,应针对具体轨道结构和车辆形式开展具体计算分析。

