基于GAM模型的鄱阳湖叶绿素a与水质因子相关性分析

袁伟皓 ，王华 *，夏玉宝 ，曾一川 ，邓燕青，李媛媛 ，张心悦

1. 河海大学环境学院，江苏 南京 210098；2. 河海大学浅水湖泊综合治理与资源开发教育部重点实验室，江苏 南京 210098；3. 江西省水文局，江西 南昌 330000

鄱阳湖是中国长江中游典型的通江湖泊，也是中国第一大淡水湖，位于江西省，地处九江、上饶、南昌三市（115°50′—116°44′E，28°25′—29°45′N），上游承接赣江、抚河、信河、饶河、修河5条主要河流来水，经湖区调蓄后由湖口注入长江，是一个季节性较强的吞吐型湖泊，在维系区域水量平衡与生态安全方面发挥着重要作用（陈炼钢等，2020；俞珊妮等，2020；陈旻坤等，2021）。近年来，随着鄱阳湖流域地区社会经济的快速发展，大量氮、磷等营养物质排入鄱阳湖水体，导致富营养化水平呈逐年上升趋势，营养盐总体维持在中营养水平，但是上升速度不断加快，一些区域甚至已经呈现富营养化水平（刘静等，2020；温春云等，2020）。

氮磷是藻类增殖的物质基础，其与藻类生物量之间的关系一直是研究湖泊富营养化的重点之一（刘静，2020；钱奎梅等，2021）。叶绿素a（Chl-a）是藻类重要的表征指标，水体中Chl-a含量的多少反映了浮游植物生物量的高低，其浓度与水环境质量密切相关，是水体理化性质动态变化的综合反映指标，在水体富营养化评价中起关键作用（陈金红等，2020）。目前，众多研究关注湖泊水质因子与Chla之间的相关性，但得出的结论都是线性、对数和正负相关等（孙越峰等，2020；朱广伟等，2020；曾一川等，2020），由于Chl-a与各水质因子之间的关系非常复杂，同时各类湖泊具有其独特的性质，尤其是针对具有典型通江特性的鄱阳湖。

常用的线性回归分析可能会忽略解释变量（Explanatory variable）与响应变量（Response variable）之间的非线性关系；同时，传统的线性分析方法不能适用多变量之间的统计学分析，而广义加性模型（Generalized Additive Model，GAM）是一种非参数的分析模型，能直接处理响应变量和多个解释变量之间的非线性关系，不需要假定数据的分布，具有很高的灵活性，近年来在环境等众多领域具有非常广泛的应用（Peng et al.，2020；贺祥等，2017；丁隆强等，2020）。但是，关于GAM模型在鄱阳湖水环境研究中的应用相对较少。程新等（2017）运用GAM模型对鄱阳湖表层水体中藻类丰度与环境因子之间的关系进行了研究，研究表明：2012年10月—2013年7月，鄱阳湖藻类丰度与水温和叶绿素a呈极显著的正相关关系，与氨氮、总磷呈极显著负相关关系。因此，深入探究鄱阳湖不同区域水质恶化和富营养化的原因显得尤为重要，构建GAM模型对鄱阳湖较长时间序列的Chl-a与水质因子进行相关性研究也十分必要。

本文运用非线性的分析方法，探讨了鄱阳湖不同区域的Chl-a变化的限制性水质指标与主要的可能因素，给出了相应的可能有效解决途径，具有十分重要的理论和实践意义，也为鄱阳湖长远的富营养化防控和有效科学的管理提供了依据。

1 材料与方法

1.1 样品采集与测定

本研究选取鄱阳湖主湖区3个典型点位，由西向东分别为蚌湖（115°58′49″E，29°18′22″N）、都昌（116°11′35″E，29°14′36″N）和蛇山（116°22′57″E，29°05′14″N），于 2016 年 1 月—2020 年 12 月开展了近5年的连续野外监测，采样频次为每月1次，每次用 2 L有机玻璃采水器采集距离湖水表层0.5 m的3组平行水样，采集的水样用500 mL聚乙烯塑料瓶收集，现场测定水温（WT）、透明度（SD）等参数，后及时带回实验室测定叶绿素a（Chl-a）、总氮（TN）、总磷（TP）、氨氮（NH3-N）和高锰酸盐指数（CODMn）。其中，叶绿素a采用丙酮萃取分光光度计法测定（杨玉珍等，2011）；总氮和总磷分别采用碱性过硫酸钾消解-紫外分光光度法（HJ 636—2012）及钼酸铵分光光度法（GB 11893-89）测定；氨氮采用纳氏试剂分光光度法测定（HJ 535—2009）；高锰酸盐指数则采用高锰酸盐指数测定法（GB 11892-89）；透明度采用塞式盘法测定；水温等则为采样现场仪器直接测定。

1.2 数据分析方法

GAM模型是广义线性模型（Generalized Linear Model，GLM）的半参数拓展，可直接拟合因变量与多个自变量之间的非线性关系，对不同的函数进行加和，找出其中的规律，适应于各种不同类型分布的函数分析（郭亮等，2017；杨佳星等，2020）。其一般表达形式如下：

式中：

g(y)——连接函数；

s(x)——连接解释变量的光滑函数；

φ——随机残差项。

GAM模型的运算通过R语言实现，数据分析通过R中的mgcv软件包实现。运用GAM模型对鄱阳湖3个研究点位Chl-a与各环境因子分别进行相关性分析，分析步骤如下：（1）基于chl-a与环境因子的Pearson相关系数，确定2个主要解释变量；（2）基于解释变量间的 Pearson相关系数大小，进行共曲线性诊断（当相关系数大于0.5时，可认为2个解释变量之间存在共曲线性，需剔除1个变量；反之，则不存在，无需剔除）；（3）基于变量预分析结果，确定GAM模型的拟合方程，代入得相关性（r2）、自由度（edf）、显著性取值（P值）、解释率（Deviance Explained，D-E）和拟合图像等结果信息（当edf=1时，变量间呈现线性关系，其值越大则代表非线性影响能力越强；P值代表统计结果的显著性水平，与评估各因子间的相关性水平类似，“*”越多显著性越强。“***”对应P<0.01，表示极显著，结果可信度高；D-E为模型对变量总体变化的解释率）（张智渊等，2018）。但样品检测结果存在一定量的异常值（有异常过大及过小的现象出现），为保证较好的代表性，异常的数据结果在后面结果中不予呈现。

2 结果与讨论

2.1 叶绿素a含量变化特征

总体而言，研究期间（2016年1月—2020年12月）3个研究点位Chl-a质量浓度的波动范围为0.0002—0.0510 mg·L−1，鄱阳湖各点位间 Chl-a 质量浓度随时间的变化明显，夏季Chl-a质量浓度普遍高于其他季节，具体如图1所示。蚌湖点位质量浓度高于其他测点，5年内整体呈现先下降后上升的趋势，且于2018—2020年夏季出现多次峰值，最大值出现在 2018年 10月，质量浓度达 0.0510 mg·L−1，5 年均值为 0.0124 mg·L−1；都昌点位 Chla 质量浓度介于 0.0002—0.0219 mg·L−1之间波动，整体趋势较为稳定，分别于2016—2017年和2020年夏季出现3次峰值，最大值出现在2020年10月，5年均值为 0.0062 mg·L−1；蛇山点位Chl-a质量浓度介于 0.0006—0.0234 mg·L−1之间波动，整体趋势也相较稳定，分别于2017年和2020年夏季出现两次峰值，最大值出现在2017年8月，5年均值为0.0057 mg·L−1。

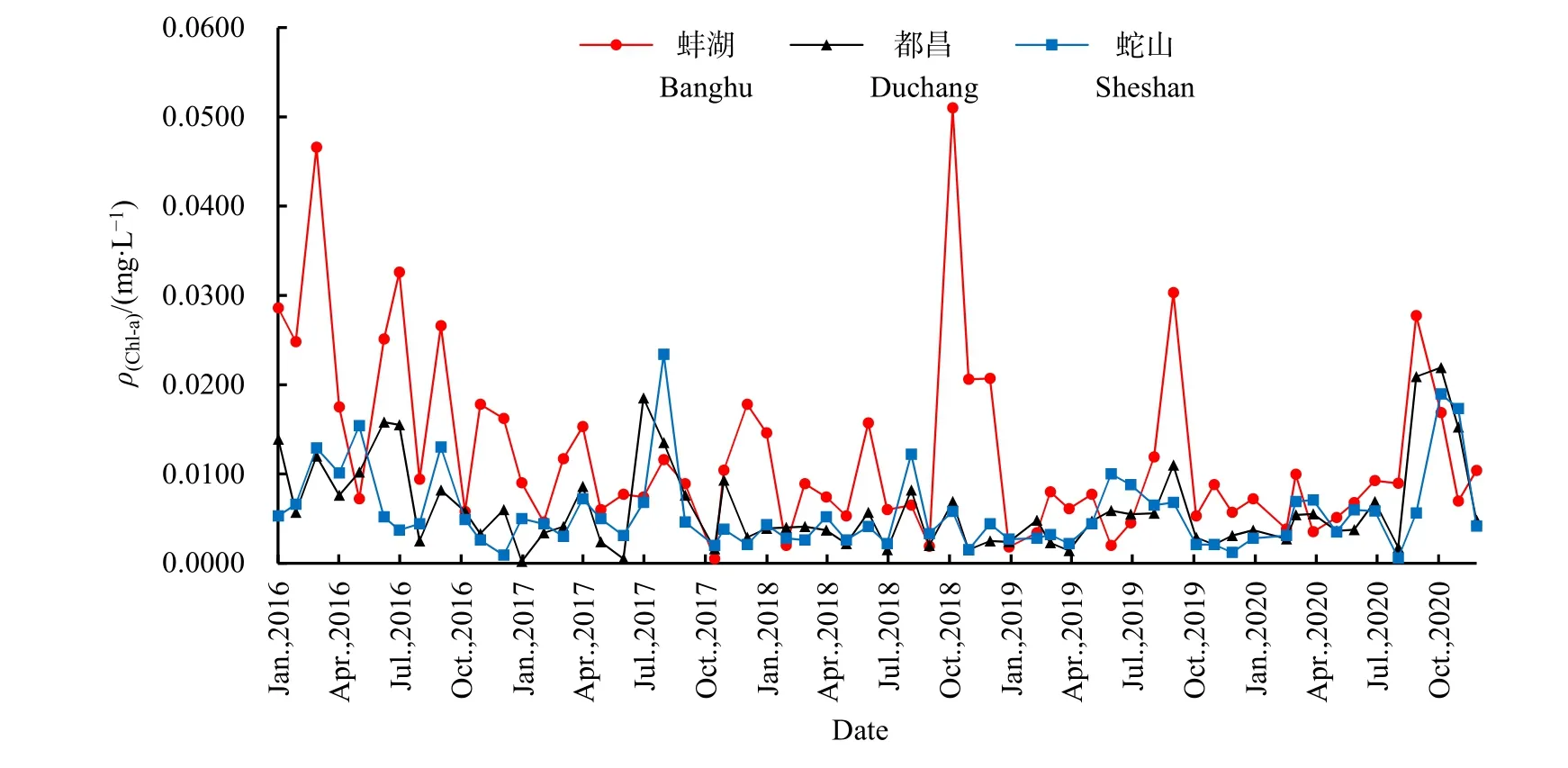
图1 研究点位叶绿素a含量变化Fig. 1 Variation of Chl-a concentration at the research sites

就蚌湖和都昌点位而言，其位于赣江下游流域，较为直接地受到赣江水质的影响。盛文涛等（2021）研究发现，近年来赣江的营养盐浓度及TN/TP显著高于其他4河，同时赣江年径流量位于5河之首，丰水期赣江携带大量营养盐通量进入鄱阳湖，在其下游附近逐渐出现满足藻类增殖条件的区域，因此该区域内Chl-a多会在丰水期结束后的时期（10月左右）达到峰值。而对于蛇山点位而言，其位于鄱阳湖东北部，李云良等（2016）研究发现鄱阳湖于高洪水位季节，污染物（营养盐等）因东北部湖湾区存在顺时针方向环流而发生长时间滞留和富集；因此，蛇山点位于8月左右达藻类增殖最佳条件（流速、营养盐和水温等），这也解释了蛇山点位Chl-a质量浓度峰值多出现在8月的原因。

2.2 环境因子变化特征

2016年1月—2020年12月鄱阳湖3个研究点位的环境因子随时间的变化见图2。就3个点位的水温而言，点位之间的差异不大，5年内呈现夏季高，冬季低的特点，夏季水温介于33.4—34.4 ℃之间波动；冬季水温则介于2.1—2.7 ℃之间波动。就透明度而言，3个点位的SD介于0.1—1.5 m之间波动，随时间变化明显，3个点位SD 5年均值由西向东分别 0.44、0.48、0.45 m。就总氮质量浓度而言，3个点位TN质量浓度呈现整体下降趋势，点位间差异不大；蚌湖点位TN质量浓度介于0.27—3.51 mg·L−1之间波动，5 年均值为 1.24 mg·L−1，于2016—2018年冬季出现多次峰值；都昌点位TN质量浓度介于0.19—2.45 mg·L−1之间波动，5年均值为1.25 mg·L−1；蛇山点位TN质量浓度介于0.34—2.78 mg·L−1之间波动，5 年均值为 1.43 mg·L−1。就总磷而言，3个点位整体质量浓度介于 0—0.125 mg·L−1之间波动，趋势相对稳定，蛇山点位于2016年3月和2017年3月出现了两次峰值，分别达到了 0.206 mg·L−1和 0.228 mg·L−1；3 个点位 5 年均值分别为 0.053、0.058 和 0.061 mg·L−1，自西向东呈现递增趋势。就氨氮而言，其变化趋势整体上与TN相似，于2016—2018年内波动显著，后两年趋向于稳定，各点位多年均值分别为0.236、0.157、0.188 mg·L−1。就高锰酸盐指数而言，蚌湖的CODMn显著大于其他点位，5年来整体质量浓度趋向于稳定，介于 1.0—3.0 mg·L−1之间波动。

图2 研究点位环境因子随时间的变化Fig. 2 Variation of environmental factors at the research sites

2.3 叶绿素a与环境因子相关性

2.3.1 蚌湖叶绿素a与环境因子的相关性

对于蚌湖点位，根据Chl-a与环境因子间的相关系数判断，TN和CODMn与Chl-a之间的相关系数较高，因此选取 TN和 CODMn为解释变量代入GAM模型；同时，TN和CODMn间的相关系数为0.18，故排除共曲线性可能，无需剔除变量。根据变量预分析结果，将TN和CODMn代入如下模型方程拟合：

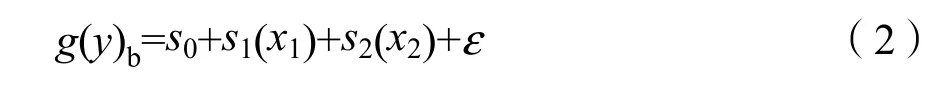
式中：

x1——蚌湖点位 TN 质量浓度（mg·L−1）；

x2——蚌湖点位 CODMn质量浓度（mg·L−1）。得到r2为0.435，TN和CODMn的自由度分别为4.79和2.40，解释率为52.3%。

从图3中可以看出，蚌湖点位Chl-a与TN和CODMn存在非线性关系，TN的非线性影响能力更强，Chl-a与TN的关系更为复杂，当TN质量浓度为0—1 mg·L−1时，TN对Chl-a的影响最为显著，两者呈现明显正相关关系；当TN的质量浓度为1—2.6 mg·L−1时，Chl-a质量浓度会随着TN的变化而略微减少；当TN的质量浓度大于2.6 mg·L−1时，二者又再次表现较明显的正相关关系。CODMn与Chl-a呈现先增大后减小的变化趋势，当CODMn的质量浓度为0—3.3 mg·L−1时Chl-a质量浓度会随着CODMn的变化而显著增加；当 CODMn的质量浓度大于3.3 mg·L−1时，Chl-a质量浓度会随着 CODMn的增加而减少。

图3 蚌湖TN和CODMn与Chl-a质量浓度的关系Fig. 3 The relationship between TN, CODMn and Chl-a in Banghu

2.3.2 都昌叶绿素a与环境因子的相关性

对于都昌点位，根据 chl-a与环境因子间的相关系数判断，SD和TN与Chl-a之间的相关系数较高，因此选取SD和TN为解释变量代入GAM模型；同时，SD和TN间的相关系数为−0.51，可能存在共曲线性，因此需剔除1个变量。

根据变量预分析结果，将SD和TN分别作为解释变量构建GAM模型，方程如下：

式中：

x1——都昌点位SD（m）；

x2表示都昌点位 TN 质量浓度（mg·L−1）。基于表1结果可得，解释变量SD的显著性和解释率均较好，拟合程度较高，因此选取SD的模型为最优模型。

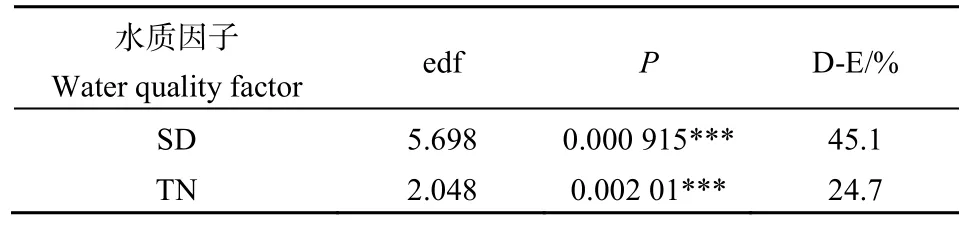
表1 GAM模型分析结果Table 1 Analysis results of GAM model

从图4中可以看出，都昌点位Chl-a与SD存在较强的非线性关系，当SD为0.2—0.6 m时，Chl-a质量浓度基本保持不变，维持在相对较低水平；当SD为0.6—0.8 m时，Chl-a质量浓度增加明显，而当介于0.8—1.2 m时，Chl-a质量浓度逐渐减少；但当SD大于1.2 m时，Chl-a质量浓度又显著增加。

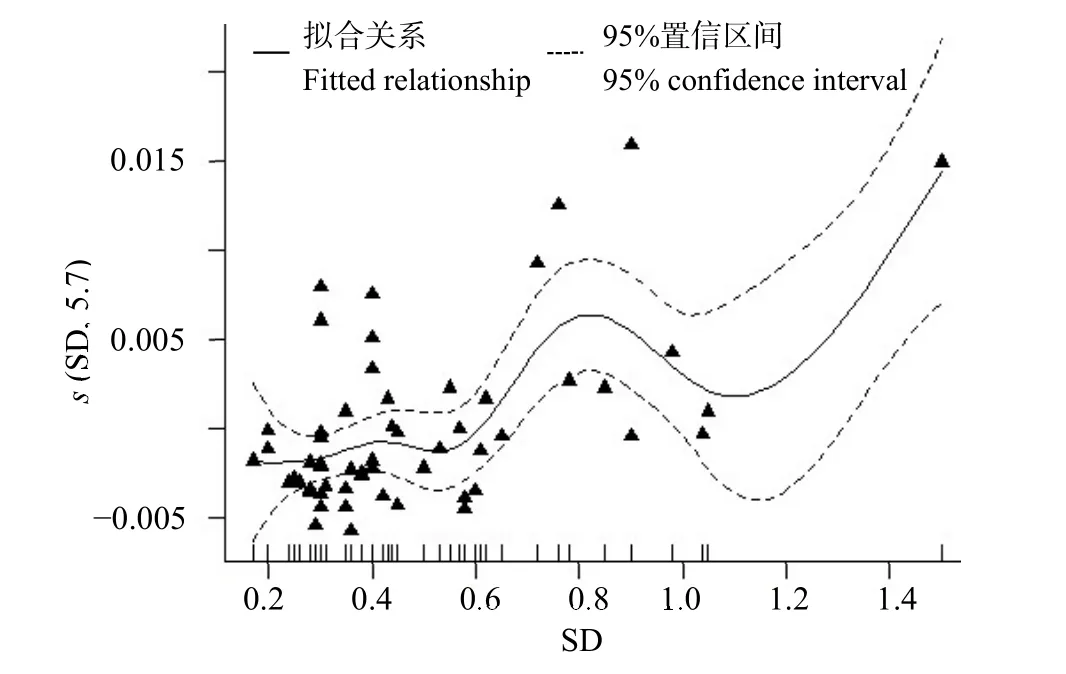
图4 都昌SD与Chl-a质量浓度的关系Fig. 4 The relationship between SD and Chl-a in Duchang

2.3.3 蛇山叶绿素a与环境因子的相关性

对于蛇山点位，根据Chl-a与环境因子间的相关系数判断，TN和CODMn与Chl-a之间的相关系数较高，因此选取 TN和 CODMn为解释变量代入GAM模型；同时，TN和CODMn间的相关系数为−0.30，故排除共曲线性可能，无需剔除变量。根据变量预分析结果，将TN和CODMn代入如下模型方程拟合：

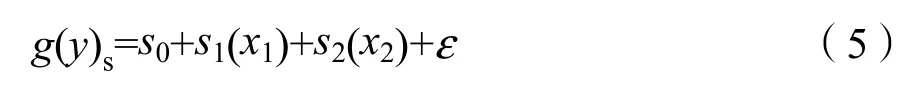
式中：

x1——蛇山点位 TN 质量浓度（mg·L−1）；

x2——蛇山点位 CODMn质量浓度（mg·L−1）。得到r2为0.627，TN和CODMn的自由度分别为5.05和5.64，解释率为71.0%，解释率较高。

从图5中可以看出，蛇山点位Chl-a与TN和CODMn存在较强非线性关系，CODMn的非线性影响能力更强，Chl-a与CODMn的关系更为复杂。当TN质量浓度为0—1 mg·L−1时，TN对Chl-a的影响最为显著，两者呈现显明显的负相关关系，当TN质量浓度大于1 mg·L−1时，Chl-a质量浓度随着TN的增加而保持相对的稳定，后出现略微减小趋势。对于Chl-a与CODMn而言，当CODMn质量浓度介于0—2 mg·L−1时，Chl-a保持相对稳定；当 CODMn质量浓度为 2.0—2.4 mg·L−1时，Chl-a质量浓度略有增长；当CODMn质量浓度大于2.4 mg·L−1时，Chla与其呈现明显的负相关关系。

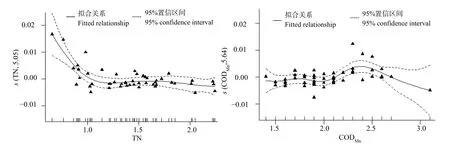
图5 蛇山TN和CODMn与Chl-a质量浓度的关系Fig. 5 The relationship between TN, CODMn and Chl-a in Sheshan

2.4 讨论

鄱阳湖3个研究点位藻类增殖与水质因子的关系存在较为显著的空间差异，位于西部的蚌湖、中部的都昌和东部的蛇山点位Chl-a质量浓度分别与TN和CODMn、SD及TN和CODMn呈现非线性关系，所得的对应解释率分别为 52.3%、45.1%和71.0%。更多地，蚌湖与蛇山点位由于地理位置的差异，Chl-a质量浓度的伴随变化也不尽相同，需要给出不同点位（区域）的限制性水质指标与主要的可能因素，并探讨相应的有效解决途径。

蚌湖属鄱阳湖营养盐质量浓度较高的点位，通过GAM模型模拟得出Chl-a与TN和CODMn存在非线性关系，TN的非线性影响能力更强，Chl-a与TN的关系更为复杂，其并未呈现随TN和CODMn质量浓度增加而增加的趋势。蚌湖点位的Chl-a质量浓度主要受到氮含量与有机物含量的限制，对于该点蓝藻水华防控而言，应当加强其TN的监控，并尽量保持相对较低水平，虽出现TN质量浓度增加而Chl-a质量浓度减少的阶段，但其可能原因是非适应性的藻类细胞死亡，而伴随着的是较强适应性的藻种成为优势藻，藻类组成发生变化（朱伟等，2008），因此会伴随该藻种的增殖与TN呈现明显的正相关关系，Chl-a质量浓度显著升高的现象；同时，也应当重点关注蚌湖点位的CODMn，尽量将有机物含量控制在相对较小的水平，尽管出现CODMn质量浓度增加而Chl-a质量浓度减小的现象，但湖泊中过多的有机物含量会间接影响水体溶解氧和微生物等因子，对水体健康不利（石玉等，2021）。

通过GAM模型拟合得出，都昌点位Chl-a与SD呈现较强且复杂的非线性关系，原因可能在于：鄱阳湖河湖相通，泥沙输入、风浪搅动、航运采砂等众多因素都会导致水体透明度下降（程时长等，1993；赖普文等，2015；李海军，2017；刘同宦等，2020）。伴随着蓝藻等浮游生物的繁殖，水体中的有机物质被利用，同时浮游生物的繁殖还可能减小风浪，降低泥沙搅动，具体表现为，在一定范围内，水体的SD与Chl-a含量之间的正相关关系。对于都昌点位的Chl-a调控，应当主要关注透明度指标，使其保持较为合理的区间，过高和过低的水体透明度对于湖泊生态环境均有一定程度的影响；同时，也应当加强都昌点位的营养盐因子调控，虽然本研究中氮磷等营养物质对于都昌点位并非关键性限制因子，但是TN/TP也可能是潜在的限制因子。

通过GAM模型拟合得出，蛇山点位Chl-a与TN和CODMn存在较强非线性关系，CODMn的非线性影响能力更强，Chl-a与CODMn的关系更为复杂，与蚌湖点位类似，蛇山也未呈现随TN和CODMn增加而增加的趋势。蛇山点位的Chl-a质量浓度主要受到有机物含量与氮含量的限制，与蚌湖点位不同，整体而言Chl-a质量浓度伴随TN和CODMn质量浓度变化的幅度不大。对于蛇山点位的Chl-a调控和蓝藻水华防控应当充分注重水质指标的综合控制，保持水体氮含量与有机物含量于合理区间内，维护该区域的水生态平衡。

本文基于GAM模型对鄱阳湖Chl-a与水质因子进行了相关性分析，但也存在一定不足：蚌湖和都昌点位的最优模型解释率中等，分别为52.3%和45.1%，原因可能为缺乏考虑风场和流场等环境因子对于Chl-a质量浓度的影响。在对鄱阳湖风场和湖流的综合研究结果显示，鄱阳湖中部和东部湖区在风场和湖流形态的双重作用下，其水流呈现“环流”现象，这也导致了水体更新时间相较鄱阳湖其他区域更长（Yuan et al.，2020），营养盐与有机物在此范围内会停留更长的时间，也可能是导致该区域近年来蓝藻水华现象频发的主要原因，过多的氮含量与有机物含量无法被利用或降解，伴随 Chl-a质量浓度与环境因子的逐渐恶化，亦可能是导致鄱阳湖水环境恶化的重要原因（Zhang et al.，2015）。可在今后的研究中加强对于鄱阳湖典型点位的风场和流场的连续监测，分析考虑综合环境因子（水文过程、气象因素和水质因子）对于鄱阳湖营养化的影响。

3 结论

鄱阳湖Chl-a的关键性水质指标与主要的可能因素的判别，对于永葆鄱阳湖“一湖清水”和水环境永续可持续发展具有重要理论和实践意义，本文的主要结论如下：

（1）鄱阳湖3个研究点位（西部蚌湖、中部都昌和东部蛇山）Chl-a与水质因子的关系存在较为显著的空间差异，其 Chl-a质量浓度分别与 TN和CODMn、SD及TN和CODMn呈现非线性关系，模型解释率分别为52.3%、45.1%和71.0%；蚌湖与蛇山点位由于地理位置的差异，Chl-a质量浓度的伴随变化也不尽相同。

（2）运用GAM模型拟合得出，蚌湖Chl-a与TN和CODMn存在非线性关系，TN的非线性影响能力更强，Chl-a与TN的关系更为复杂，蚌湖点位的Chla质量浓度主要受到氮含量与有机物含量的限制，对于该点蓝藻水华防控应注意控制较低的氮含量和合理范围的有机物含量；都昌点位Chl-a与SD呈现较强且复杂的非线性关系，对于都昌点位的 Chl-a控制，应当主要关注透明度指标，但TN/TP也可能是潜在的限制因子；蛇山点位Chl-a与TN和CODMn存在较强非线性关系，CODMn的非线性影响能力更强，Chl-a与CODMn的关系更为复杂，对于蛇山点位的藻类或蓝藻水华防控，需要充分注重水质指标的综合控制，不仅仅局限于营养盐与有机物含量。

（3）鄱阳湖不同区域Chl-a质量浓度与各水质因子的相关程度不尽相同，区别于太湖等湖泊，鄱阳湖因其特殊的性质，具有复杂的风场和湖流形态特征，在今后的研究中应当加强对于鄱阳湖风场和流场的连续监测，分析考虑综合环境因子（水文过程、气象因素和水质因子等）对于鄱阳湖营养化的影响。