龙门吊车双闭环鲁棒PID控制

乌鲁木齐市博安兴业机械制造有限公司 张 博

龙门吊车提升装置采用柔性物体，使得整个吊车总体重量小，工作效率高。但是，柔性绳索也会存在一些弊端，最突出问题便是重物提升过程中的摇摆问题。为解决这一难题，在双闭环PID的基础上加入鲁棒控制更好的解决摇摆问题。通过对控制系统灵敏度设计得出吊车系统参数的变化范围，进而得到控制器相关参数。仿真结果证明当绳长和物体重量在给定范围内变化时，本文设计控制器可以有效解决重物摆动问题，具有良好的工程应用前景。

本文通过设计龙门吊车防摇摆控制系统，实现了对重物摆动问题的有效控制，极大程度提升了吊车工作效率。对于解决防摇摆问题，双闭环PID控制消除摆动效果较好，但吊车的柔性绳索长度和重物载荷质量通常情况下是变化的，因此，设计的控制器应该鲁棒性较好。

鲁棒控制的优点就是当系统数学模型难以求解以及求解不准确或系统内部参数频繁变化以及施加外部扰动时，系统仍然可以保持原有目标性能。

本文通过对控制器灵敏度参数设计进而推导出整个鲁棒控制器其他设计参数。这里鲁棒性能是指吊车系统对未考虑因素的灵敏度，主要包括干扰和未建模动态特性等。最后利用Simulink仿真对所设计的鲁棒PID控制器进行了验证，仿真结果表明双闭环鲁棒PID能够很好地消除重物提升过程中的摆动问题。

龙门吊车是用于工厂、码头和集装箱货场的装卸与运输作业的一种运载工具。它在空中轨道运行，占地面积小、工作效率高。在对吊车摆动问题进行讨论时，需要先将吊车系统进行简化、抽象。整个工作过程如图1所示。

图1 起重机数学模型

1 龙门吊车数学模型建立

图中M为小车质量，m为重物质量，F为小车受到的牵引力，f为导轨方向摩擦阻力。

小车的位置与重物的位置坐标为：

所以小车和重物的速度分量为：

系统的动能为：

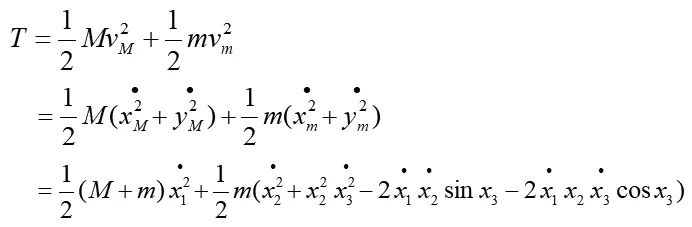
系统的拉格朗日方程为：

综合以上公式得系统的方程组为：

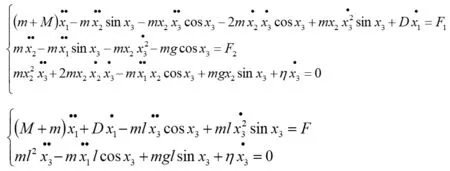
进行拉氏变换可得系统传递函数为：

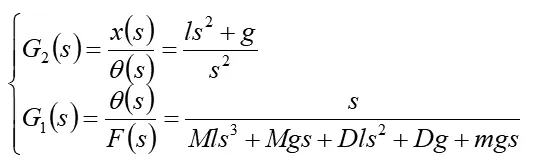
2 数学模型验证

通过在simulink中对比传递函数和简化后的微分方程得到的仿真结果，可以看出小车位移和摆角曲线基本重合，因此，上述过程对微分方程的简化是可行的。模型验证仿真图如图2所示。

图2 模型验证仿真图

3 双闭环鲁棒PID控制器设计

控制系统设计时，通常已经建立了精确地控制系统数学模型，但是，在实际工程问题中，存在很多我们没有考虑到的影响因素，如内部和外部参数的变化，外部施加的扰动以及系统未建模动力学特性等等，因此我们得到的数学模型往往是实际工程问题物理模型的粗糙模型。

设计鲁棒控制系统的目的是因为鲁棒控制灵敏度低，在给定的一定参数变化区域内能够保持系统预期性能，当所建立数学模型不够精确时，或者其他参数不断变化时，系统仍然能够保持原有的稳定性。双闭环控制原理图如图3所示。

图3 双闭环控制原理图

对系统模型进行简化，忽略系统阻尼，可得到简化后的传递函数：

内环（摆角）设计：

取M=50kg，标称值分别取m=5kg，l=1m，所以内环系统未校正时的传递函数为：

选用合适的PID控制器的形式：内环PID反馈控制器有PI、PD、PID三种形式

综上，分析传递函数零极点在复平面分布可知，基于结构简单并且闭环系统稳定性的原则，这里选用PD控制作为反馈控制器。

内环加上反馈PD控制器后的内环传递函数为：

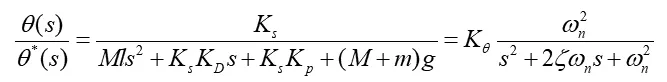
为了是系统具有较好的鲁棒性能，即对于绳长和负载质量的频繁变化不敏感，在鲁棒性的基础上对内环PD控制进行参数设计，如果灵敏度低，则证明鲁棒性好。

可得系统对摆长l的灵敏度为：

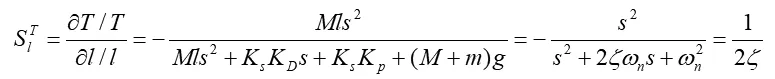
系统对重物质量m的灵敏度为：

为使系统对内部及外部参数变化灵敏度较低，通常要求在内部参数在一定范围内变化时运动轨迹的变化尽量小于5%，在此条件下，重物质量和吊车摆长允许变化的范围是：

为了使内环系统响应速度较快且超调量尽量小，取ζ=1，由灵敏度公式可以得出摆长在0.9m到1.1m范围内变化。同时为使内环系统跟随性能较好，内环系统响应时间应该尽可能短，转折角频率ωn应选的较大；但ωn取得过大时，系统稳定性变差。取ωn= 8rad/s，因此载荷在1.19kg到21kg范围内变化。

综上可知，当内环控制器取KD=29,KP=95时，内环将具有抑制“摆长0.9m到1.1m变化，质量1.19kg到21kg变化的能力”外环（位置）设计内环调节所需要的时间相对于外环调节来说较小，将内环等效成为一个比例环节，可以便于外环设计：

这里为满足近似条件，采用5倍系数，可得：

外环控制器鲁棒性设计：

PD反馈调节器的传递函数为H2(s) = 1+K2s，为了快速、准确定位，在前向通道添加比例调节器G(s) =K1，所以二次积分环节闭环传递函数为：

比例环节闭环传递函数为：

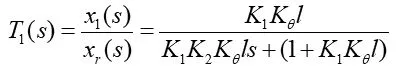
综上所述，可以得到图4所示的系统控制框图。

图4 控制原理图

为了安全考虑，需要使电机输出的最大的的控制力不超过一定范围，因此摆角参数设置以及电机的电压参数设置之前设置限幅环节，使电机所能输出的最大力矩不超过限定值。这样可使系统超调得到减小，因而系统稳定性也有所提升。

由图5所示的仿真结果图可以看出，在双闭环鲁棒PID控制下，摆角曲线在10s左右达到稳定且超调小。位置曲线同样在10s内趋于稳定；同时重物质量与绳长在给定变化范围之内变化时，系统灵敏度均小于5%，在仿真实验过程中，当参数超出变化范围的时候，控制系统同样具有良好的抗扰动性能，同时可以保证控制系统的稳定性以及较小超调量。

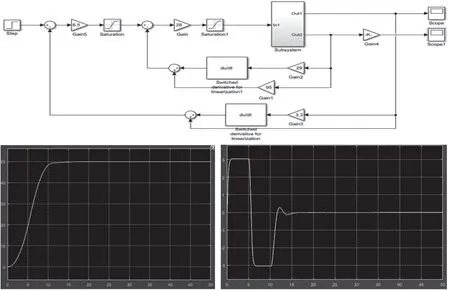
图5 仿真结果