高液静压无心磨床磨削过程再生颤振的稳定性分析*

徐 磊，赵丽梅，余 炯

(贵州大学机械工程学院，贵阳 550025)

0 引言

随着工业的发展，原有的零件加工方式因加工精度不高和效率低下，已无法满足工业的需求，无心磨削方式的出现为工业零件的高精度和高效率生产提供了解决方案，目前，无心磨床已经广泛应用于航空航天、汽车、冶金、电力等领域圆柱形、无中心孔的短轴和圆锥体等零件的生产[1]。我国对无心磨床的研究起步较晚，近年来，为突破国外的技术封锁，缩小与国外在无心磨削领域的差距，国内研究人员在无心磨床的自主研发方面做了大量的研究工作，但在磨削精度和效率方面与国外的无心磨床相比仍然存在较大的差距。其中造成磨床加工精度低下的主要原因在于砂轮磨削工件时发生颤振[2]。因此，从无心磨床磨削过程再生颤振机理出发，分析无心磨削的稳定性，来提高无心磨床磨削稳定性，从而提高加工精度是很有必要的[3]。

纵观国内外对机床切削颤振的研究，有很多研究人员做了很多卓有成效的工作。文献[4]研究了单自由度再生颤振模型，通过磨削力表达式的推导，结合振动方程分析磨削稳定性，并引入了同时考虑工件及砂轮再生颤振的双再生效应理论。文献[5]通过建立的切入磨再生颤振动力学模型，利用工件表面波纹度幅值的增长率为稳定性判据，研究再生颤振对磨削工件系统稳定性的影响。文献[6]在分析外圆磨削过程的颤振增长机理的基础上，提出了再生颤振原理的外圆磨削动力学建模方法，来研究外圆磨削的稳定性。文献[7]推导了机床再生型切削颤振系统极限切削宽度随主轴转速变化的计算公式，提出了机床切削系统稳定性极限预测方法。文献[8]以外圆磨床磨削过程为研究对象，提出了一种用于双再生外圆磨削过程稳定性分析的系统方法，能够直接从频谱中获取参数空间的稳定特性，而不需要使用时域响应。以上研究均取得了一定的研究成果，但在对机床颤振的研究中，主要是对车床、铣床和普通外圆磨床的研究，对无心外圆磨床的研究则涉及较少，而且，在建立颤振模型时，没有考虑砂轮在磨削工件时产生的摩擦力，同时忽视了再生的磨削力和摩擦力对工件表面成形的影响，因此得出的结论具有很大的局限性，还无法指导实际生产。

本文以高液静压无心磨床无心磨削系统为研究对象，在分析高液静压无心磨床结构工作原理和实际加工的基础上，来研究无心磨削的颤振机理；抓住高液静压无心磨床磨削过程的特殊性，设定了特殊的坐标系，建立了同时考虑砂轮和工件的再生和摩擦效应的无心磨削再生颤振数学模型，并计算稳定性分析的特征值，结合数值延拓算法得到稳定性叶瓣图，为选择合适的加工工艺参数来避免颤振提供理论依据。

1 高液静压无心磨床结构原理分析及磨削过程再生颤振机理研究

1.1 无心磨床的结构原理分析

高液静压无心磨床的工作原理分析对其工作过程的颤振机理研究和稳定性分析具有至关重要的作用，因此，对高液静压无心磨床进行结构分析和工作原理分析是十分必要的。本文以贵州省某厂生产的HFC-1808型高液静压无心磨床为研究对象，磨床的装配结构图如图1所示。高液静压无心磨床由磨削工件的砂轮，支承并带动工件旋转的导轮，支承工件的托板，对砂轮的尺寸、形状、几何角度进行修整的砂轮修整器，对导轮的形状、尺寸和几何角度等进行修整的导轮修整器，滑台，导轨，机座等组成[9]。待加工的工件放在砂轮、导轮和托板之间，由托板和导轮进行支承，在导轮的带动下旋转，并通过砂轮对工件进行磨削；砂轮固定在机座上，导轮和托板安装在滑台上，滑台由导轨支承，通过滑台在导轨上的移动来实现工件的进给，进而达到加工精度，很明显，高液静压无心磨床的磨削方式为切入式进给磨削。

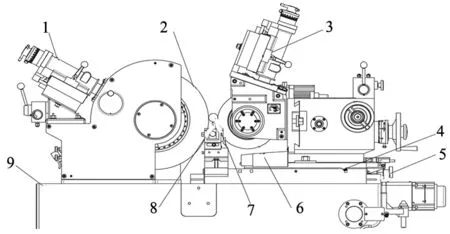
1.砂轮修整器 2.砂轮 3.导轮修整器 4.滑台5.导轨 6.导轮 7.工件 8.托板 9.机座图1 高液静压无心磨床装配结构图

1.2 无心磨削过程的再生颤振机理研究

在高液静压无心磨床切入式无心磨削过程当中，磨削轮用磨粒切割并再生工件表面，导轮带动工件旋转，并推动工件实现径向进给，变相的使固定不动的砂轮完成径向和圆周方向的进给。当工件被砂轮连续摩擦时，工件与砂轮之间产生的磨削力相互推离。根据再生颤振理论可知，磨削力和瞬时磨削深度之间存在着正比的关系[10]。磨削深度的任何变动都会引起磨削力的变化，因此时变的磨削力会激发砂轮与工件的振动，砂轮和工件的位移会影响磨削深度和磨削力，只要系统阻尼不足，这个状态就会保持，这种自激振动称为再生颤振。因此，为了更好了解再生效应的磨削动力学，提出了一种基于再生理论的动力学数学模型。由于托板的表面是由耐磨损材料制作而成，故在高液静压无心磨床磨削过程当中，托板的磨损很小，对工件的再生效应可以忽略不计。另外，导轮是调整轮，控制工件的运动，没有参与工件的磨削，因此，对工件再生表面的影响忽略不计。

2 高液静压无心磨床磨削过程再生颤振动力学模型

2.1 无心磨削过程的数学模型

高液静压无心磨床磨削示意图如图2所示，Rg为砂轮的直径，m；Mg为质量，kg；Cg为阻尼系数，N/(m/s)；Kg为刚度，N/m；ωg为磨削工件的旋转速度，rad/s；Rw为工件的直径，m；Mw为质量，kg；Cw为阻尼系数，N/(m/s)；Kw为刚度，N/m；ωw为旋转速度，rad/s；工件在导轮和托板的推动下，以进给速度f(m/rev)向砂轮进给。以砂轮的回转中心为原点，砂轮和工件的公法线方向为X轴，垂直于公法线方向为Y轴建立坐标系。基于所建立的坐标系，砂轮磨削工件的动力学控制方程可以离散为：

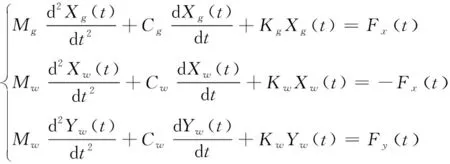
(1)

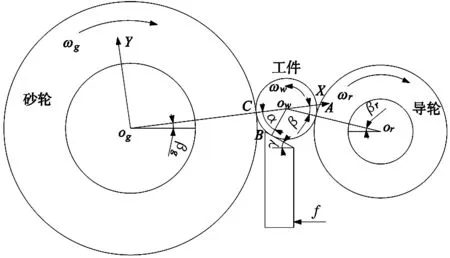
图2 高液静压无心磨床磨削示意图

2.2 切入式无心磨削磨削力

在高液静压无心磨床磨削工件的过程当中，给磨削系统带来不稳定的最主要的原因主要是砂轮和工件之间的磨削力，结合外圆磨床磨削力理论，提出了一种针对于切入式无心磨床砂轮磨削工件的磨削力模型；磨削力可以分解为垂直工件径向的切向力Ft、沿工件径向的径向力Fn和沿工件轴向的轴向力Fa，其中轴向力最小，可以忽略不计，切向磨削力对砂轮的影响较小，为简化问题，在砂轮的动力学模型中，将切向磨削力忽略，只考虑径向磨削力对砂轮的影响，结合式(1)可知，Fx和Fy分别表示工件在X方向和Y方向的激振力，并分别等于工件的径向磨削力Fn和切向磨削力Ft。

Fx=Fn
Fy=Ft

(2)

结合高液静压无心磨床的工作原理可知，该无心磨床是利用砂轮磨削工件，而砂轮作为磨料磨削工具，由其上的结合剂固定的小颗粒磨料来研磨工件，从而产生时变的磨削力[11]。砂轮磨削工件表现出的外在的磨削力，实际上是由无数个单个磨粒磨削工件产生的切削力和滑擦力的合力，据此提出了图3所示的单个磨粒磨削工件产生切削力和摩擦力的示意图，由图可知，在高液静压无心磨床磨削工件的过程中，砂轮的每个磨粒对工件表面进行切削和摩擦，并产生切向和法向的切削力和摩擦力[10]。

fct=ψfcn
fft=μffn

(3)

式(3)中，fct和fcn分别表示切削力在切向和径向的分量，fft和ffn分别表示滑擦力在切向和径向的分量，μ是摩擦系数，ψ是一种取决于磨粒平均尖端角的无量纲比。

(a) 砂轮磨削工件示意图 (b) 单个磨粒磨削示意图 (c) 磨削中各力分量图3 单个磨粒产生切削力和摩擦力示意图

在高液静压无心磨床磨削工件的过程中，将所有参与磨削的磨粒算在内计算磨削力，得到总的径向和切向磨削力如式(2)所示[13]：

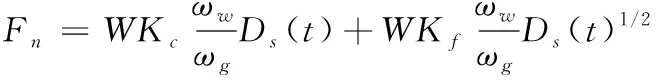
(4)

其中，Kc是切削过程系数，N/m2；Kf是滑擦过程系数，N/m3/2；W为工件的宽度；Ds(t)为取决于磨削进给和砂轮-工件相对位移的瞬时磨削深度。

根据再生理论来确定磨削深度Ds(t)，同时考虑工件进给和工件与砂轮的相对位移，则磨削深度为：

Ds(t)=fcos(βg)+Xw(t)-Xg(t)-εYw(t)
(0<ε<1)

(5)

磨削是一个工件材料连续被砂轮移除生成新表面的过程，因此，在先前(t-Tw)时工件和砂轮相对位移的任何变动，都会影响瞬时磨削深度Ds(t)，则磨削深度Ds(t)变为：

Ds(t)=fcos(βg)+(Xw(t)-Xg(t)-εYw(t))-

Xw(t-Tw)-Xg(t-Tw)-εYw(t-Tw)

(6)

而且，在磨削过程中，砂轮是不断磨损生成新表面的过程，因此，在双再生效应的影响下，磨削深度Ds(t)变成：

Ds(t)=fcos(βg)+(Xw(t)-Xg(t)-εYw(t))-

Xw(t-Tw)-Xg(t-Tw)-εYw(t-Tw)-

g(Xw(t-Tg)-Xg(t-Tg)-εYw(t-Tg))

(7)

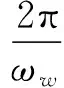
除了再生效应，利用一个符号函数来考虑滑擦，则式(4)中砂轮和工件之间的摩擦系数μ是切向相对速度Vf的函数。

μ=sign(Vf)μd

(8)

如图4所示，砂轮和工件之间的切向相对速度Vf取决于砂轮和工件的旋转，二者的平面运动，即：

Vf=Vfg-Vfw

(9)

图4 砂轮和工件在接触区切向相对速度示意图

式中，Vfg和Vfw分别是砂轮和工件在接触区的切向速度：

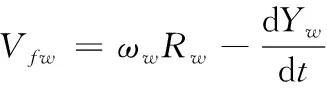
(10)

3 高液静压无心磨床磨削过程稳定性分析

在1965年，自Tobias首次提出稳定性叶瓣图的概念开始[14]，稳定性叶瓣图逐步发展并作为一种在切削加工规划阶段用来预测切削稳定性和用来解释机床动态切削过程行为的一种方法，并被大家广泛接受。但是，在稳定性叶瓣图的构建当中，人们只热衷于车床或铣床切削过程稳定性叶瓣图的构建，对切入式无心磨床磨削过程稳定性叶瓣图的构建，几乎没有涉猎。因此本节尝试从构建切入式无心磨床磨削过程稳定性叶瓣图的角度出发，来研究高液静压无心磨床磨削过程稳定性。

在高液静压无心磨床稳定磨削的过程中，令X(t)=[xg(t)xw(t)yw(t)]T，将式(4)、式(8)～式(10)代入式(1)，可以得到如下磨削模型:

(11)

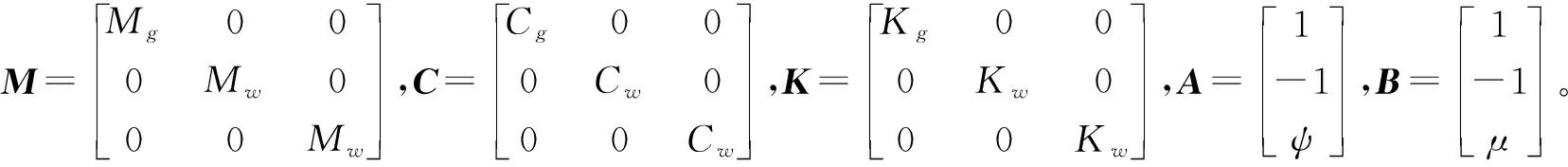
本文以MK1808型高液静压无心磨床为研究对象，将要用于计算和分析的参数值列于表1。

表1 稳定性仿真参数值

通过MATLAB编程对式(11)来进行特征值计算并结合数值延拓算法得到HFC-1808型高液静压切入磨无心磨床的稳定性叶瓣图(如图5所示)，该图以砂轮转速为横坐标，工件的径向磨削深度为纵坐标。

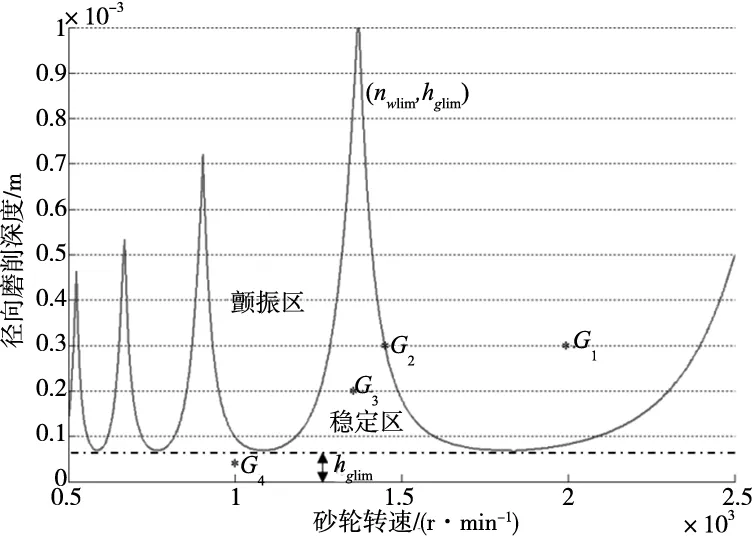
图5 高液静压无心磨床磨削稳定性叶瓣图

图5所示的砂轮再生颤振稳定性叶瓣图，由不同的临界点连接而成，并将整个平面分成两个区域，每个区域具有不同的稳定性性质，依据稳定性性质的不同可分成4个稳定性区域。

(1)切入式无心磨削颤振区：当砂轮转速和径向磨削深度匹配点完全位于曲线上方时，如图中的G1点，砂轮要发生再生颤振，这时无论怎样选择砂轮转速和磨削深度，砂轮磨削工件都会发生颤振，从而引发一系列的危害，因此，切入式无心磨削颤振区应坚决避免。

(2)切入式无心磨削临界稳定区：当砂轮转速和径向磨削深度匹配点刚好落在曲线上时，如图中G2点，为切入式无心磨削临界稳定区，此时，砂轮磨削工件可能会发生颤振，也可能稳定的磨削，总之，只要颤振发生，就会严重影响工件的磨削精度，因此，切入式无心磨削临界稳定区也是应该避免的区域。

(3)切入式无心磨削有条件稳定区：当砂轮转速和径向磨削深度匹配点落在极限磨削点划线hlim和叶瓣图曲线之间时，如图中G3点，为切入式无心磨削有条件稳定区；当砂轮转速固定不变，随着径向磨削深度的增加，匹配点先后经过稳定区和颤振区，砂轮先稳定后发生颤振；当固定径向磨削深度，随着砂轮转速的增加，稳定区和颤振区相间出现。

(4)切入式无心磨削无条件稳定区：当砂轮转速和径向磨削深度匹配点落在极限磨削点划线以下时，如图中G4点，为切入式无心磨削无条件稳定区，在此区域，无论如何选择砂轮转速和径向磨削深度，砂轮都不会发生颤振。

综上所述，结合高液静压无心磨床稳定性叶瓣图，可以选取适当工艺参数，从而避免砂轮磨削工件时颤振的发生(颤振状态即为不稳定状态)，从而达到提高加工精度和生产效率的目的。并且，高液静压无心磨床磨削稳定性叶瓣图为企业在生产加工时的参数选择提供了依据，同时，也为相关磨床的稳定性分析提供了新的思路。

4 结论

(1)应用再生颤振理论，得出高液静压无心磨床磨削工件时的不稳定原因主要是因为砂轮和工件发生了再生颤振引起的。

(2)以再生颤振机理为基础，建立了同时考虑砂轮和工件再生颤振的动力学模型。

(3)求解动力学模型矩阵方程，利用MATLAB编程得到高液静压无心磨床切入式无心磨削稳定性叶瓣图，并根据砂轮转速和径向磨削深度匹配点的不同，将稳定性叶瓣图划分为4个区域，为磨削工艺参数的选择提供了理论依据。