变截面开孔组合钢梁楼盖设计分析

崔巨宏

(北京市建筑设计研究院有限公司， 北京 100045)

0 概述

中心城区的高层、超高层办公建筑的建筑高度、平面尺寸易受制于城市规划条件及周边既有邻近建筑的影响。但是业主普遍希望能够实现使用层数最大化、空间高度适宜、造价经济，这与结构构件尺度、机电管线排布相矛盾。而变截面开孔组合钢梁楼盖可实现机电管线与结构梁交叉布置，有效解决结构梁、机电管线占用室内空间过多的问题，增大吊顶高度和使用净高，减小建筑层高，增加使用层数，降低甲方造价。但是关于变截面开孔组合钢梁楼盖的研究较少，本文对比了有限元算法与规范算法得到结果的差异，分析了几何参数对楼盖性能的影响，提出了构造建议。

1 工程概况

某高层办公楼建筑高度60m，外框架柱至核心筒的办公区跨度为12，15.3m，办公楼标准层结构平面图、剖面图分别见图1,2。业主希望办公区净高不小于2.7m，若标准层层高3.9m，地上建筑最高可建15层，实现建筑面积最大化。但标准层层高3.9m，扣除净高2.7m、面层110mm，结构梁板和机电管线可用的总高度仅1.09m，常规做法难以实现业主需求，但是变截面开孔组合钢梁楼盖技术，可以解决这个问题。

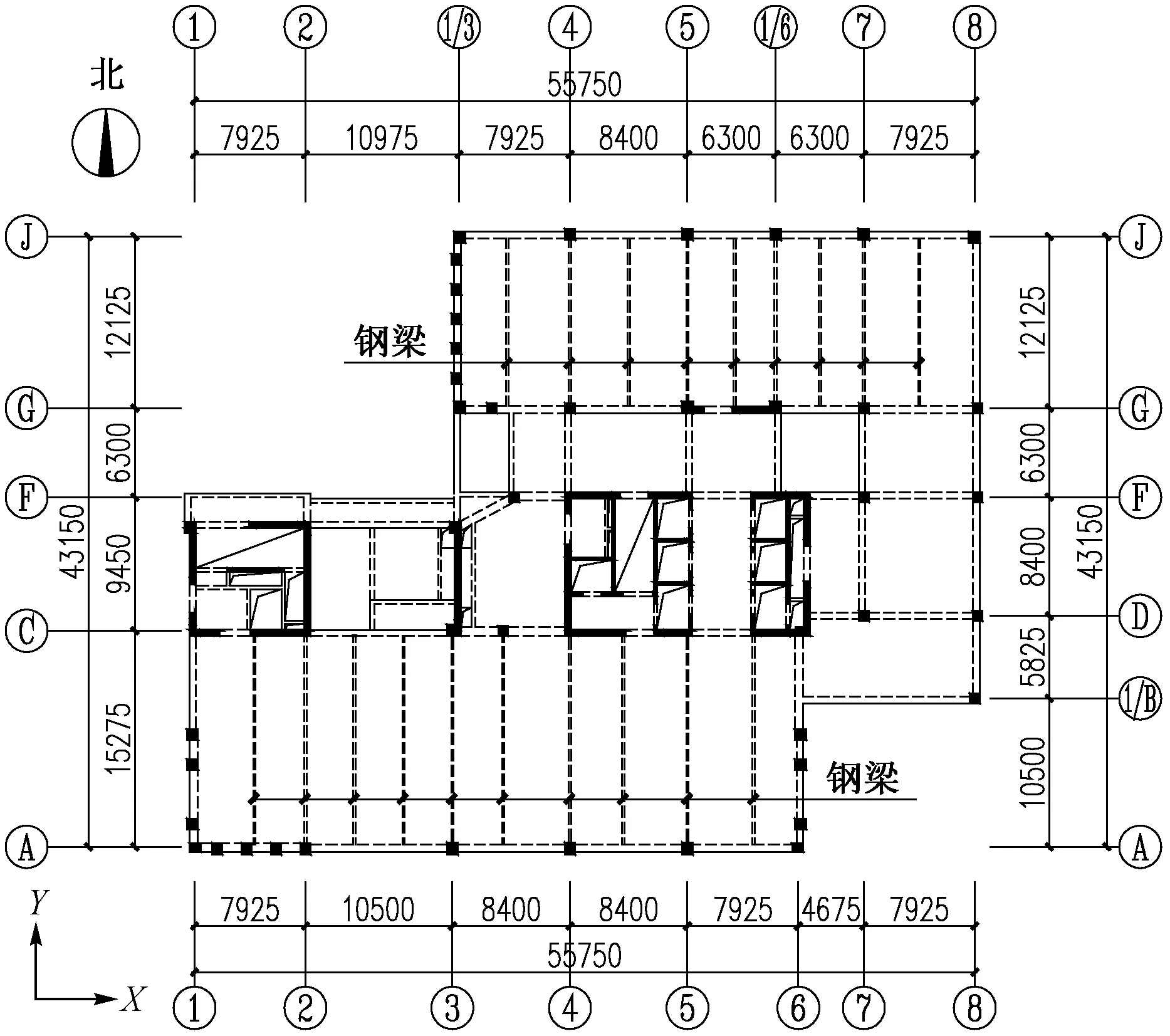
图1 标准层结构平面图

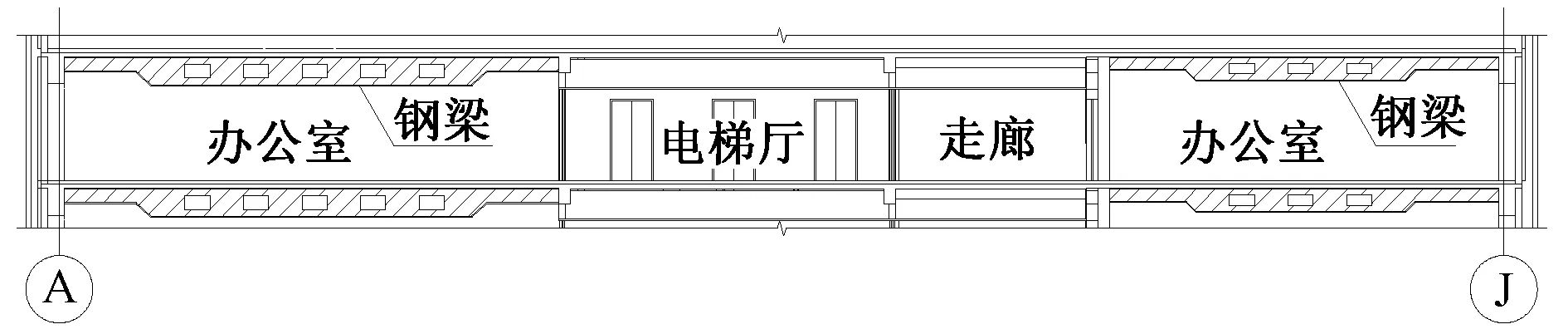
图2 标准层剖面图

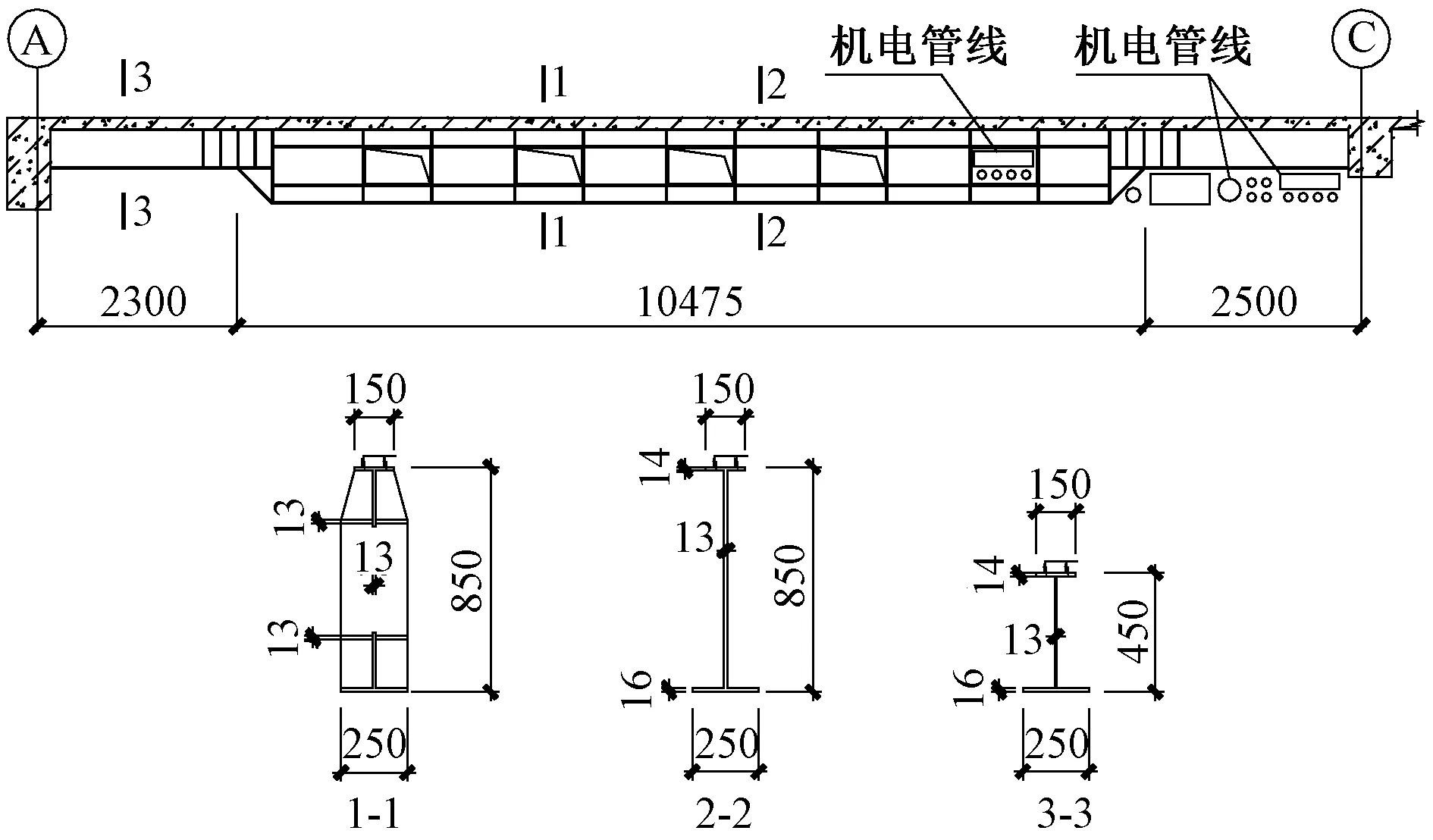
图3 楼盖钢梁立面、截面图

2 有限元分析

楼盖钢梁(图2)端部变截面，腹板开孔，且按组合梁进行设计，所以受力情况复杂。分别对钢梁按规范算法和几何非线性有限元算法(SATWE软件和MIDAS Gen软件)进行分析，分别对钢梁按规范算法和几何非线性有限元算法进行分析，比较、验证规范算法对变截面开孔组合钢梁的适用性。

组合钢梁设计参数为楼面恒载2.5kN/mm2，楼面活载3.0kN/mm2，舒适度分析时，楼面有效分布活载0.5kN/mm2，混凝土楼板厚度130mm；钢梁材质Q355B，混凝土强度等级C30；根据文献[1]的规定，混凝土翼缘板有效宽度为2 600mm。

在SATWE软件中模拟钢梁时，按钢梁实际截面输入，由于在开孔处采用了加劲板，可保证截面刚度与抗剪承载力不低于未开孔区域。在MIDAS Gen软件中模拟钢梁时，假定混凝土、钢材均为理想弹性材料；钢梁腹板、加劲肋、上下翼缘按“板单元”模拟，混凝土楼板按实体单元模拟。钢梁的腹板、翼缘按约100mm的尺寸划分网格，混凝土楼板分为2层，对应钢梁按约100mm的尺寸划分水平网格，楼盖钢梁有限元分析模型见图4。文献[3-5]研究结果表明，组合钢梁抗剪连接件栓钉，应根据其变形协调及剪力传递的特点，考虑滑移效应。通过钢梁上翼缘与混凝土楼板设置弹性连接的方式模拟栓钉连接，以与规范算法跨中钢梁Z向变形一致为原则控制弹簧的刚度。在钢梁边界(A点)设置3个Y，Z向约束，模拟钢梁简支节点，且保证模型中梁端的转动能力；在混凝土楼板横向边界(B，C点)设置1排X向约束，模拟主体结构对构件的X向约束；在混凝土楼板纵向边界(C，D点)设置3排Y向约束，模拟主体结构对构件的Y向约束及绕X轴的转动约束。对钢梁楼盖进行舒适度分析时，结构阻尼比为2%。

图4 楼盖钢梁有限元分析模型

2.1 应力分析

根据《钢结构设计标准》(GB 50017—2017)[1](简称钢结构标准)中“对于不直接承受动力荷载以及板件宽厚比满足塑性调幅设计方法要求的组合钢梁，由于考虑塑性调幅设计方法，组合梁的承载力极限状态验算不必考虑施工方法和顺序的影响。”施工时钢梁下可设置临时支撑，消除施工方法和顺序对钢梁竖向变形的影响。

按规范算法计算的考虑滑移效应的钢梁跨中处应力比为0.49(应力为149.5N/mm2)，钢梁变截面处应力比为0.60(应力为183.0N/mm2)；钢梁跨中挠度为28.5mm。

按有限元算法计算的考虑滑移效应的钢梁应力见图5。从图5中可得，钢梁跨中下翼缘处Mises应力最大值为175.0N/mm2，为规范算法的1.17倍；变截面处Mises应力最大值为260.1N/mm2，为规范算法的1.42倍。跨中洞口处钢梁全截面应力的平均值约95N/mm2，为规范算法的0.63；与洞口相邻处钢梁全截面应力平均值约82N/mm2，为规范算法的0.55；变截面处钢梁全截面应力平均值约141N/mm2，为规范算法的0.77。

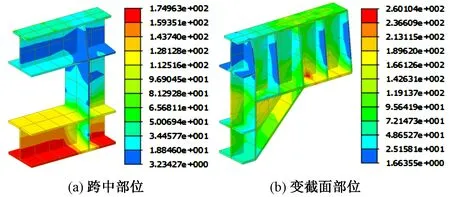
图5 考虑滑移效应钢梁应力图/(N/mm2)

可见采用规范算法对变截面开孔组合钢梁进行计算分析时，弹性阶段材料的应力结论与有限元算法计算得到的结论存在一定误差。根据钢结构标准中组合钢梁强度计算的相关规定，考虑钢梁全截面塑性工作，钢梁正应力区的应力图形为矩形。因有限元算法得到的钢梁应力为弹性分析结果，钢梁尚未进入塑性，应力为三角形分布，故有限元算法得到的钢梁抗弯效率更高，具体表现为：应力极值高于规范算法结果，截面平均应力小于规范算法结果。规范算法的结果较可靠，且偏于安全。

2.2 楼盖舒适度分析

在MIDAS Gen程序中，采用有限元算法分别对单根钢梁及6根组合钢梁组成的25m宽楼盖进行舒适度分析，楼盖第1阶自振模态及步行节点荷载见图6。从图6可知，单根钢梁的第1阶自振频率的理论计算值为4.90Hz，为规范算法的1.24倍；整体楼盖的第1阶自振频率的理论计算值为4.05Hz，为规范算法的1.025倍。

图6 楼盖第1阶自振模态及步行节点荷载

单根钢梁有限元模型中，因楼板宽度较窄，受楼板边界条件影响，钢梁的自振频率较高，为避免边界条件造成舒适度结论失真，有必要按整体模型模拟分析；按有限元算法及规范算法计算得到的楼盖自振频率的结果十分接近。变截面开孔组合钢梁楼盖自振频率按规范算法计算是可行的。

大量研究发现，一般情况下多人不同步行走下，楼板响应很少超过单人行走的楼板响应。因此，选取单人行走的工况来分析楼板在行人荷载下的振动。在有限元模型中(图6)，根据楼盖第1阶自振模态分析结果来布置人行荷载，由楼盖中部钢梁的跨中(A点)行走至相邻钢梁跨中(B点)，激振质量为70kg，步长约0.7m，步频分别为2，3，4，5Hz。

不同步频人行荷载作用下楼盖各激励点的振动峰值加速度见图7。从图7可得，单人行走频率为2，3，4，5Hz时，楼盖对应振动峰值加速度为0.014，0.021，0.029，0.042m/s2，楼盖的振动峰值加速度最大值为规范算法的0.91。因激振质量仅为楼盖质量的0.18%，共振现象不显著，振动峰值加速度随激振频率的提高而增加，在建筑实际使用中，单人以5Hz的频率通过楼盖为小概率事件，可见与给定路径单人行走激振的有限元算法相比，按规范算法得到的结论偏安全。

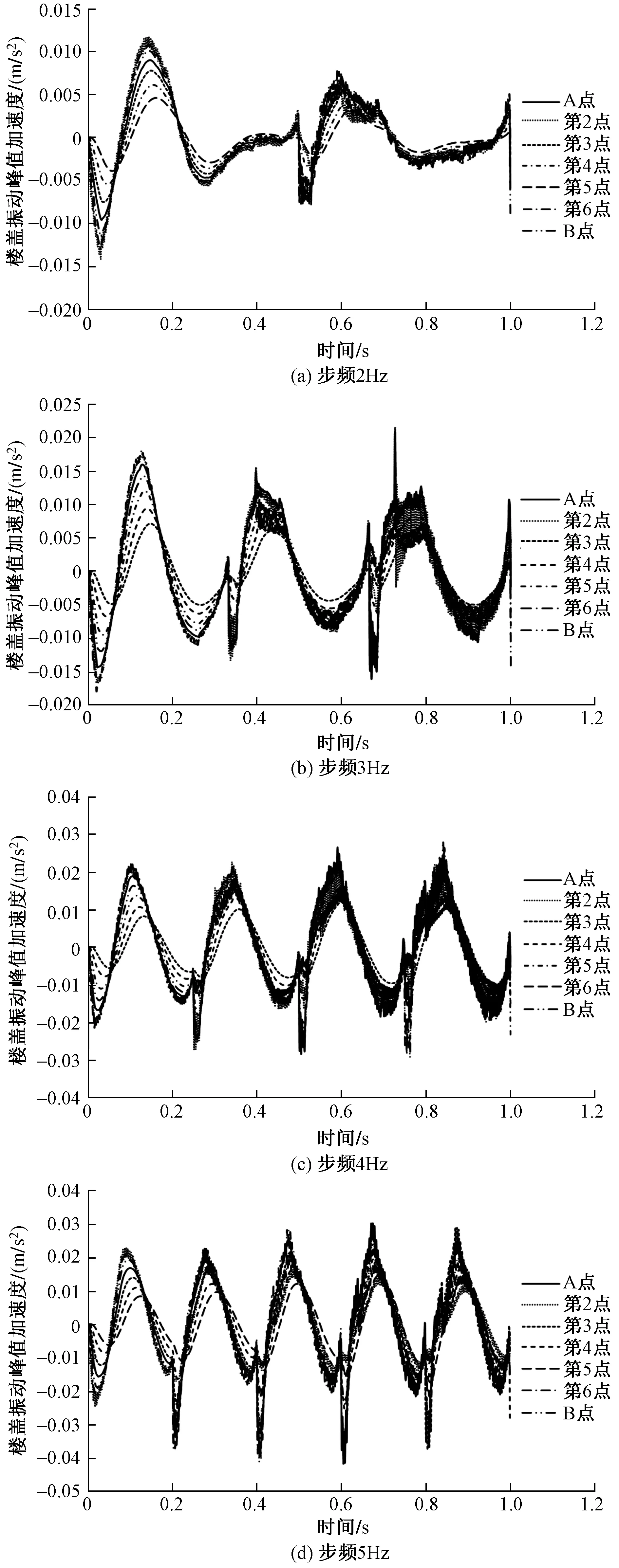
图7 不同步频人行荷载作用下楼盖各激励点的振动峰值加速度/(m/s2)

3 几何参数的影响

3.1 变截面段长度

钢梁几何参数如图8所示，设钢梁跨度为L，跨中段钢梁截面高度为H，变截面段钢梁高度为h，跨度为l，变截面段的钢梁跨高比设n，变截面段钢梁下供机电管线通过空间的横截面面积为A。近似A=l(H-l/n)，故当l=Hn/2时，梁下供机电管线通过空间的横截面面积取得最大值；将n=h/l代入A=l(H-l/n)，得h=H/2，即当变截面段钢梁跨高比为定值，则变截面段高度h为跨中高度H的1/2时，变截面段梁下供机电管线通过空间的面积A取得最大值。

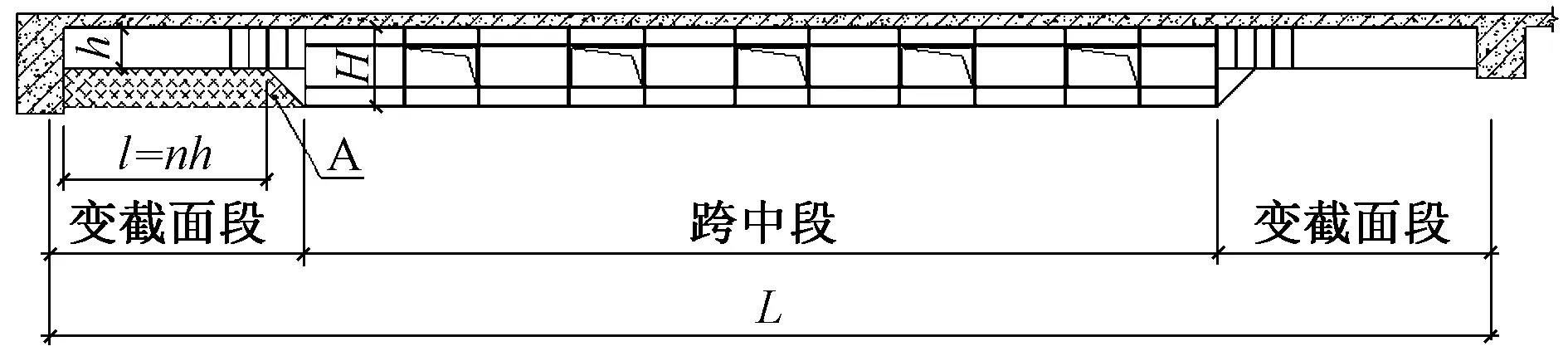
图8 钢梁几何参数

控制变截面段梁高、翼缘宽度、翼缘和腹板厚度等参数不变，取钢梁变截面段长度l为1 850mm(约0.12L)、2 050mm(约0.135L)、2 300mm(约0.15L)、2 500mm、(约0.165L)、2 750mm(约0.180L)，分别按规范算法及有限元算法分析不同变截面段长度的钢应力、变形、舒适度指标，结果见表1。从表1可得，随变截面段长度的增加，钢梁端部的弯矩近似线性增加，钢梁应力随之线性增加；钢梁跨中竖向变形、自振频率、峰值加速度受变截面段长度影响不大。工程设计中，可视使用空间需求，合理设置变截面段长度，必要时可适当增加板厚，以满足应力要求。

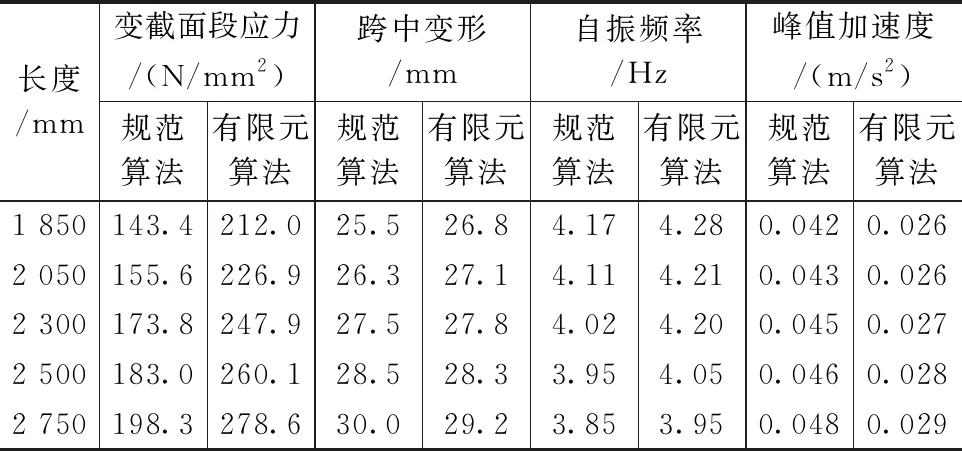
表1 不同变截面段长度的钢梁指标对比

3.2 开孔的影响

控制钢梁截面不变，对开孔数量分别为3,4,5,6个的钢梁模型进行计算分析。图9(a)～(c)模型中，跨中腹板分别开3，4，5个孔，开孔尺寸均为750mm×400mm；图9(d)模型中，跨中腹板开孔6个开孔尺寸为500mm×400mm，图9(b)，(d)模型的开孔率相同。

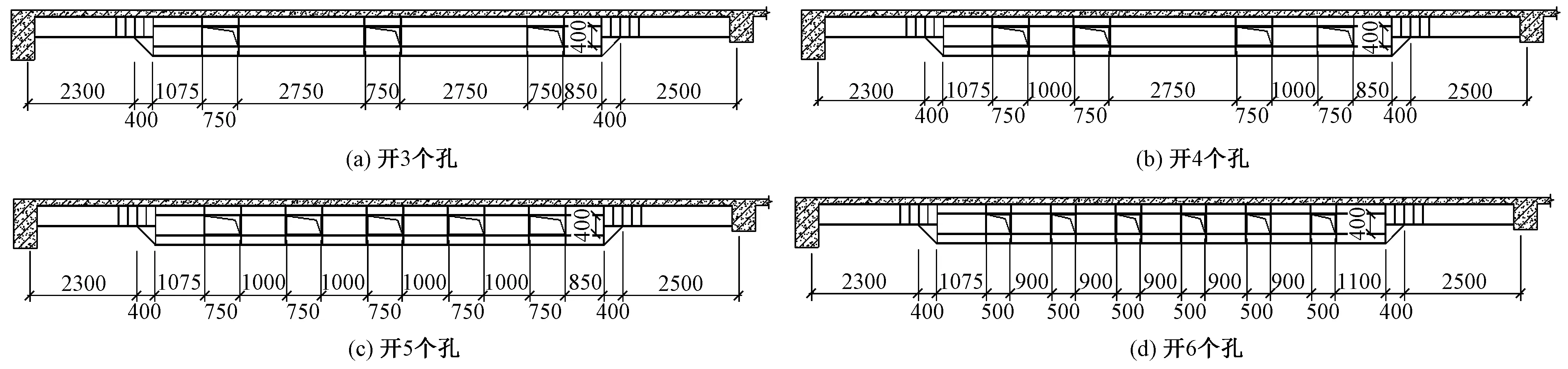
图9 钢梁的不同开孔方式

采用有限元算法分析的钢梁跨中应力、竖向变形、舒适度指标见表2。从表2可知，开孔数量(2～6个孔)、开孔率(10.9%～18.2%)、相同开孔率下(14.6%)不同开孔分布对钢梁的跨中应力、竖向变形及舒适度指标无显著影响，工程设计中，为获得最大开孔率，可根据构造要求，在钢梁跨中段开满预留孔。

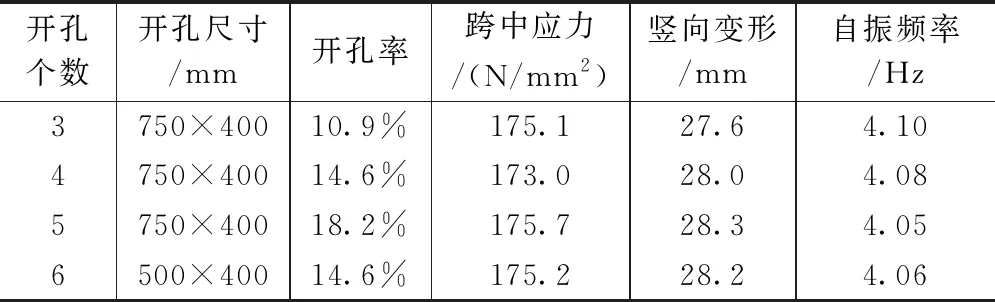
不同开孔形式的钢梁指标对比 表2

4 加强措施

4.1 混凝土翼板

文献[10]表明，组合钢梁有3种典型的破坏状态：1)混凝土翼板压溃的弯曲型破坏；2)抗剪连接件的剪切破坏；3)混凝土翼板的纵向剪切破坏。钢梁上翼缘与混凝土板抗剪可靠连接且混凝土板内横向配筋率较高的组合梁，表现为混凝土翼板压溃的弯曲型破坏。当钢梁下翼缘屈服后，截面中和轴不断上升。当中和轴进入到混凝土翼板内且混凝土最大弯曲拉应力超过其抗拉强度时，混凝土翼板开始出现裂缝，且随荷载增加 ，横向裂缝增多，最终跨中混凝土被压碎。

设计荷载作用下，钢梁上翼缘受拉，纵向剪力通过栓钉传递到混凝土楼板。钢梁混凝土板应力见图10。从图10可知，钢梁端变截面处的混凝土楼板底部出现最大拉应力区，折算后的平均拉应力为4.0N/mm2，混凝土受拉区的厚度约20mm。

图10 组合钢梁混凝土板应力图/(N/mm2)

4.2 孔边加劲肋

根据文献[1]的腹板开孔补强要求，可仅沿孔边设加劲肋补强，因腹板开孔率较高，参考文献[1]中矩形孔长度大于梁高时的做法，横向加劲肋沿梁全高设置；孔边纵向加劲肋间距仅余400mm，可拉通纵向加劲肋，孔边加劲肋的做法见图11。采用有限元算法，分别对按构造补强钢梁和加劲肋贯通补强钢梁分析。跨中处不同孔边加劲肋补强做法的钢梁应力图见图12、不同孔边补强做法的钢梁应力、变形、舒适度指标见表3。

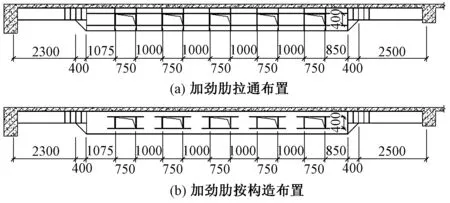
图11 孔边加劲肋做法示意图

图12 跨中处不同孔边加劲肋补强做法的钢梁应力图/(N/mm2)

表3 不同孔边补强做法的钢梁指标对比

图12和表3结果表明，加劲肋贯通布置，纵向加劲肋的抗弯能力得以发挥；与按构造补强钢梁相比，加劲肋贯通布置增加了少量用钢量，钢梁最大应力比降低约8%，腹板应力比降低约40%；将钢梁腹板分为若干区格，可提高钢梁的局部稳定；孔边加劲肋补强做法对楼盖的变形及舒适度指标则影响不大。

5 结论与建议

(1)经有限元计算验证，采用规范算法，可以保证钢梁应力、变形、舒适度等结论的可靠性，且偏于安全。

(2)钢梁的开孔数量、分布对其应力、变形及舒适度无显著影响，建议工程设计中，在钢梁跨中段按构造开满预留孔以获得最大开孔率。建议变截面段梁高为跨中高度的一半，必要时可适当增加板厚，以满足应力要求。

(3)建议变截面开孔组合钢梁顶部设置暗梁，承担楼板底部出现的拉应力，延缓混凝土楼板横向开裂，提高组合钢梁的抗弯承载能力；在钢梁变截面相关区域，可适当加大楼板配筋率，减小钢筋间距。加强边框架柱与核心筒、内框架柱的连接。建议钢梁孔边加劲肋贯通布置，以降低钢梁应力，提高钢梁的局部稳定。